DOCSLIB.ORG

Chapter 1 Introduction of Boundary Layer Phenomena Main Topics

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Chapter 1 Introduction of Boundary Layer Phenomena Main Topics Chapter 1 Introduction of boundary layer phenomena T-S Leu Jan. 13, 2018 Main Topics • History of Fluid Mechanics Development • Idea of Boundary Layer • Boundary Layer Equations 1 Fluid Mechanics Development History EFD: Ideal fluid: Real fluid : Hot wire MEMS Inviscid flow (zero drag) Hot film Viscosity PIV 2000s Lagrangian/Eulerian Viscous flow Boundary LDV MD Potential flow Laminar/ layer 1990s 1980s DNS (Inviscid+Irrotational) Turbulent flow Ludwig 1960~70s CFD Osborne Prandtl Panel Turbulence Reynolds 1904 method modeling 1842~1912 Lagrange Richard (1827~1845) (1736~1813) 1842~1919 Feynman has Navier Laplace Lord described Cauchy Jean (1749~1827) Rayleigh turbulence as Poisson D'Alembert Hydrodynamic the most St. Venant Isaac 1752 1755 instability: important Stokes Newton 1738 Leonhard Taylor Rayleigh unsolved 1687 Daniel Euler Navier- Kelvin Helmholtz problem of Bernoulli Stokes Benard cells classical physics. 89y Equation Bernoulli Equation 2 Bernoulli equation (I) BERNOULLI’S EQUATION (II) & integration BERNOULLI’S EQUATION AERODYNAMICS (W2-1-2) 3 BERNOULLI’S EQUATION FOR AN IRROTATION FLOW incompressibl e Steady Irrotational No gravity AERODYNAMICS (W2-1-2.1) Unsteady Bernoulli Equation This is not a very useful result in general since ∂vs/∂t can change dramatically from one point to another; to use this in practice we need to be able to draw streamline shapes at each instant in time. It works especially for simple cases such as impulsively started confined flows where streamlines have the same shape at each instant and we are interested in time required to start the flow. 4 Exercise 1 Flow out of a long pipe connected to a large reservoir, (1)find the steady state velocity v2 in the pipe after the the transient stage (2)find the transient velocity v2 in the pipe changing with time during the transient stage Back to History D'Alembert's paradox •Influid dynamics, d'Alembert's paradox is a contradiction reached in 1752 by French mathematician Jean le Rond d'Alembert. • D'Alembert proved that for incompressible and inviscid potential flow –thedrag force is zero on a body moving with constant velocity relative to the fluid. • Zero drag is in direct contradiction to the observation of substantial drag on bodies moving relative to fluids, such as air and Jean le Rond d'Alembert (1717- water; especially at high velocities 1783) corresponding with high Reynolds numbers. https://en.wikipedia.org/wiki/D%27Alembert%27s_paradox Back to History 5 Lagrangian/Eulerian Description in Fluid Mechanics Assignment: Watch the video about Lagrangian/Eulerian Description in Fluid Mechanics https://www.youtube.com/watch?v=mdN8OOkx2ko (MP4) METHODS OF DESCRIPTION • Lagrangian description => System • Eulerian description => Control volume Ch 1-2 6 Lagrangian Description • Attention is focused on a material volume (MV) and follow individual fluid particle as it move. • The fluid particle is colored, tagged or identified. • Determining how the fluid properties associated with the particle change as a function of time. Example: one attaches the temperature-measuring device to a particular fluid particle A and record that particle’s temperature as it moves about. TA = TA(t)=T (xo,yo,zo, t) where particle A passed through coordinate (xo,yo,zo) at to The use of may such measuring devices moving with various fluid particles would provide the temperature of these fluid particles as a function of time. Ch 1-2 Eulerian Description • Attention is focused on the fluid passing through a control volume (CV) fixed in the space. • Obtaining information about the flow in terms of what happens at the fixed points in space as the fluid flows past those points. • The fluid motion is given by completely prescribing the necessary properties as a functions of space and time. Example: one attaches the temperature-measuring device to a particular point (x,y,z) and record the temperature at that point as a function of time. T = T ( x , y , z , t ) => field concept. The independent variables are the spatial coordinates ( x , y , z) and time t Ch 1-2 7 Field Representation of flow • At a given instant in time, any fluid property ( such as density, pressure, velocity, and acceleration) can be described as a functions of the fluid’s location. This representation of fluid parameters as functions of the spatial coordinates is termed a field representation of flow. • The specific field representation may be different at different times, so that to describe a fluid flow we must determine the various parameter not only as functions of the spatial coordinates but also as a function of time. • EXAMPLE: Temperature field T = T ( x , y , z , t ) • EXAMPLE: Velocity field V u(x, y, z,t) i v(x, y, z,t) j w(x, y, z,t) k Ch 1-2 Nature and Transformation of Lagrangian and Eulerian Description • It is more nature to apply conservation laws by using Lagrangian description (ie. Material Volume). • However, the Eulerian description (ie. Control Volume) is preferred for solving most of problem in fluid mechanics. • The two descriptions are related and there is a transformation formula called material, total or substantial derivative between Lagrangian and Eulerian descriptions. Ch 1-2 8 Material Derivative (I) • Let (x,y,z,t) be any field variable, e.g., ρ, T, V=(u,v,w), etc. (Eulerian description) • Observe a fluid particle for a time period t as it flows (Langrangian description) • During the time period, the position of the fluid particle will change by amounts x , y , z, while its vale of will change by an amount t x y z t x y z x y z • As one follow the fluid particle, ( , , ) (u,v, w) So t t t D x y z lim u v w Dt t0 t t x t y t z t t x y z which is called the material, total, or substantial derivative. Ch 1-3 Material Derivative (II) • Use the notation D/Dt to emphasize that the material derivative is the rate of change seen by an observer “following the fluid.” • The material derivateive express a Langrangian derivative in terms of Eulerian derivatives. • In vector form, D u v w (V ) Dt t x y z t • May also use the “index notation” and Einstein’s “summation convention” (i.e, summing over repeated indices) to write D uk Dt t xk Where (x1,x2,x3)≡(x,y,z) and (u1,u2,u3)≡(u,v,w) Note: The repeated index that us summed over is called a “dummy index”; one that is not summed is called a “free index”. Back to History 9 Potential Flow Theory Inviscid & Irrotational flow GOVERNING EQUATION FOR IRROTATIONAL, INCOMPRESSIBLE FLOW: LAPLACE’S EQUATION Continuity equation Incompressible: constant For incompressible flow: there exists a streamfunction For irrotational flow: there exists a velocity potential Laplace’s equation y= 0 For irrotational, incompressible flow, there are velocity potential and For irrotational, incompressible streamfunction that both satisfy flow: y Laplace’s equation. 2 2 2 0 x2 y2 2 2 2 0 Laplace’s equation x2 y2 AERODYNAMICS (W2_1_6) 10 Potential Flow Theory • Governing equation for Potential flow is Laplace equation 2 2 2 0 x2 y2 • Laplace’s equation is a second-order linear partial differential equation. If 1, 2, 3, … , n represent n separate solutions of Laplace’s equation, then =1+2+3+… +n is also a solution of Laplace’s equation. • Complex potential with conformal mapping Boundary Condition for LAPLACE’S EQUATION Boundary Conditions: Infinite boundary conditions: Wall boundary conditions: or or 11 Fluid Flow Governing Equations • Mass conservation => Continuity equation • Momentum equation F=ma=d(mV) /dt => Navier Stokes Equation •1st Thermaldynamic law (Conservation of Energy) => Energy equation Fluid Flow Governing Equations • Continuity equation: D uk (uk ) 0 t xk Dt xk • Momentum (N-S) equation: u u p u u u j j k i j [ uk ] ( ) f j t x x x x x x x k j j k i j i • Energy equation: e e uk T ( uk ) p (k ) t xk xk xi x j u u u u ( k )2 i j j xk x j xi xi 12 2 Navier-Stokes Equations Full N-S equation 3 u u p u u u j j k i j [ uk ] ( ) f j t x x x x x x x k j j k i j i u For incompressible flows, V k 0 xk u u p u u j j i j [ uk ] f j t x x x x x k j i j i For incompressible flows with constant viscosity , u u p u 2u p 2u j j i j j [ uk ] f j f j t x x x x 2 x 2 k j j i xi j xi For incompressible ,inviscid fluids =0, uj uj p [ uk ] f j The Euler equations t xk x j e e uk T ( uk ) p (k ) t xk xk x j x j u u u u ( k )2 i j j e C T v xk x j xi xi T T u 2T k for constant C & k Cv ( uk ) p k 2 v t xk xk x j 2 T T T for incompressible flow Cv ( uk ) k 2 with constant Cv & k t xk x j 2 T T uk T for inviscid flow with Cv ( uk ) p k 2 constant Cv & k t xk xk x j T T 2T for incompressible inviscid Cv ( uk ) k 2 flow with constant C & k t xk x j v 13 where where 14 Molecular and Statistical Approaches • Fluids consist of molecules whose motion is governing by the law of dynamics. • The macroscopic phenomena are assume to arise from the molecular motion of the molecules.
Load more

Recommended publications
  • Glossary Physics (I-Introduction)
    1 Glossary Physics (I-introduction) - Efficiency: The percent of the work put into a machine that is converted into useful work output; = work done / energy used [-]. = eta In machines: The work output of any machine cannot exceed the work input (<=100%); in an ideal machine, where no energy is transformed into heat: work(input) = work(output), =100%. Energy: The property of a system that enables it to do work. Conservation o. E.: Energy cannot be created or destroyed; it may be transformed from one form into another, but the total amount of energy never changes. Equilibrium: The state of an object when not acted upon by a net force or net torque; an object in equilibrium may be at rest or moving at uniform velocity - not accelerating. Mechanical E.: The state of an object or system of objects for which any impressed forces cancels to zero and no acceleration occurs. Dynamic E.: Object is moving without experiencing acceleration. Static E.: Object is at rest.F Force: The influence that can cause an object to be accelerated or retarded; is always in the direction of the net force, hence a vector quantity; the four elementary forces are: Electromagnetic F.: Is an attraction or repulsion G, gravit. const.6.672E-11[Nm2/kg2] between electric charges: d, distance [m] 2 2 2 2 F = 1/(40) (q1q2/d ) [(CC/m )(Nm /C )] = [N] m,M, mass [kg] Gravitational F.: Is a mutual attraction between all masses: q, charge [As] [C] 2 2 2 2 F = GmM/d [Nm /kg kg 1/m ] = [N] 0, dielectric constant Strong F.: (nuclear force) Acts within the nuclei of atoms: 8.854E-12 [C2/Nm2] [F/m] 2 2 2 2 2 F = 1/(40) (e /d ) [(CC/m )(Nm /C )] = [N] , 3.14 [-] Weak F.: Manifests itself in special reactions among elementary e, 1.60210 E-19 [As] [C] particles, such as the reaction that occur in radioactive decay.
    [Show full text]
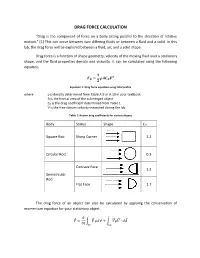
  • Drag Force Calculation
    DRAG FORCE CALCULATION “Drag is the component of force on a body acting parallel to the direction of relative motion.” [1] This can occur between two differing fluids or between a fluid and a solid. In this lab, the drag force will be explored between a fluid, air, and a solid shape. Drag force is a function of shape geometry, velocity of the moving fluid over a stationary shape, and the fluid properties density and viscosity. It can be calculated using the following equation, ퟏ 푭 = 흆푨푪 푽ퟐ 푫 ퟐ 푫 Equation 1: Drag force equation using total profile where ρ is density determined from Table A.9 or A.10 in your textbook A is the frontal area of the submerged object CD is the drag coefficient determined from Table 1 V is the free-stream velocity measured during the lab Table 1: Known drag coefficients for various shapes Body Status Shape CD Square Rod Sharp Corner 2.2 Circular Rod 0.3 Concave Face 1.2 Semicircular Rod Flat Face 1.7 The drag force of an object can also be calculated by applying the conservation of momentum equation for your stationary object. 휕 퐹⃗ = ∫ 푉⃗⃗ 휌푑∀ + ∫ 푉⃗⃗휌푉⃗⃗ ∙ 푑퐴⃗ 휕푡 퐶푉 퐶푆 Assuming steady flow, the equation reduces to 퐹⃗ = ∫ 푉⃗⃗휌푉⃗⃗ ∙ 푑퐴⃗ 퐶푆 The following frontal view of the duct is shown below. Integrating the velocity profile after the shape will allow calculation of drag force per unit span. Figure 1: Velocity profile after an inserted shape. Combining the previous equation with Figure 1, the following equation is obtained: 푊 퐷푓 = ∫ 휌푈푖(푈∞ − 푈푖)퐿푑푦 0 Simplifying the equation, you get: 20 퐷푓 = 휌퐿 ∑ 푈푖(푈∞ − 푈푖)훥푦 푖=1 Equation 2: Drag force equation using wake profile The pressure measurements can be converted into velocity using the Bernoulli’s equation as follows: 2Δ푃푖 푈푖 = √ 휌퐴푖푟 Be sure to remember that the manometers used are in W.C.
    [Show full text]
  • Chapter 4: Immersed Body Flow [Pp
    MECH 3492 Fluid Mechanics and Applications Univ. of Manitoba Fall Term, 2017 Chapter 4: Immersed Body Flow [pp. 445-459 (8e), or 374-386 (9e)] Dr. Bing-Chen Wang Dept. of Mechanical Engineering Univ. of Manitoba, Winnipeg, MB, R3T 5V6 When a viscous fluid flow passes a solid body (fully-immersed in the fluid), the body experiences a net force, F, which can be decomposed into two components: a drag force F , which is parallel to the flow direction, and • D a lift force F , which is perpendicular to the flow direction. • L The drag coefficient CD and lift coefficient CL are defined as follows: FD FL CD = 1 2 and CL = 1 2 , (112) 2 ρU A 2 ρU Ap respectively. Here, U is the free-stream velocity, A is the “wetted area” (total surface area in contact with fluid), and Ap is the “planform area” (maximum projected area of an object such as a wing). In the remainder of this section, we focus our attention on the drag forces. As discussed previously, there are two types of drag forces acting on a solid body immersed in a viscous flow: friction drag (also called “viscous drag”), due to the wall friction shear stress exerted on the • surface of a solid body; pressure drag (also called “form drag”), due to the difference in the pressure exerted on the front • and rear surfaces of a solid body. The friction drag and pressure drag on a finite immersed body are defined as FD,vis = τwdA and FD, pres = pdA , (113) ZA ZA Streamwise component respectively.
    [Show full text]
  • Kármán Vortex Street Energy Harvester for Picoscale Applications
    Kármán Vortex Street Energy Harvester for Picoscale Applications 22 March 2018 Team Members: James Doty Christopher Mayforth Nicholas Pratt Advisor: Professor Brian Savilonis A Major Qualifying Project submitted to the Faculty of WORCESTER POLYTECHNIC INSTITUTE in partial fulfilment of the requirements for the degree of Bachelor of Science This report represents work of WPI undergraduate students submitted to the faculty as evidence of a degree requirement. WPI routinely publishes these reports on its web site without editorial or peer review. For more information about the projects program at WPI, see http://www.wpi.edu/Academics/Projects. Cover Picture Credit: [1] Abstract The Kármán Vortex Street, a phenomenon produced by fluid flow over a bluff body, has the potential to serve as a low-impact, economically viable alternative power source for remote water-based electrical applications. This project focused on creating a self-contained device utilizing thin-film piezoelectric transducers to generate hydropower on a pico-scale level. A system capable of generating specific-frequency vortex streets at certain water velocities was developed with SOLIDWORKS modelling and Flow Simulation software. The final prototype nozzle’s velocity profile was verified through testing to produce a velocity increase from the free stream velocity. Piezoelectric testing resulted in a wide range of measured dominant frequencies, with corresponding average power outputs of up to 100 nanowatts. The output frequencies were inconsistent with predicted values, likely due to an unreliable testing environment and the complexity of the underlying theory. A more stable testing environment, better verification of the nozzle velocity profile, and fine-tuning the piezoelectric circuit would allow for a higher, more consistent power output.
    [Show full text]
  • A Numerical Comparison of Symmetric and Asymmetric Supersonic Wind Tunnels
    A Numerical Comparison of Symmetric and Asymmetric Supersonic Wind Tunnels by Kylen D. Clark B.S., University of Toledo, 2013 A thesis submitted to the Faculty of Graduate School of the University of Cincinnati in partial fulfillment of the requirements for the degree of Master of Science Department of Aerospace Engineering and Engineering Mechanics of the College of Engineering and Applied Science Committee Chair: Paul D. Orkwis Date: October 21, 2015 Abstract Supersonic wind tunnels are a vital aspect to the aerospace industry. Both the design and testing processes of different aerospace components often include and depend upon utilization of supersonic test facilities. Engine inlets, wing shapes, and body aerodynamics, to name a few, are aspects of aircraft that are frequently subjected to supersonic conditions in use, and thus often require supersonic wind tunnel testing. There is a need for reliable and repeatable supersonic test facilities in order to help create these vital components. The option of building and using asymmetric supersonic converging-diverging nozzles may be appealing due in part to lower construction costs. There is a need, however, to investigate the differences, if any, in the flow characteristics and performance of asymmetric type supersonic wind tunnels in comparison to symmetric due to the fact that asymmetric configurations of CD nozzle are not as common. A computational fluid dynamics (CFD) study has been conducted on an existing University of Michigan (UM) asymmetric supersonic wind tunnel geometry in order to study the effects of asymmetry on supersonic wind tunnel performance. Simulations were made on both the existing asymmetrical tunnel geometry and two axisymmetric reflections (of differing aspect ratio) of that original tunnel geometry.
    [Show full text]
  • A Concept of the Vortex Lift of Sharp-Edge Delta Wings Based on a Leading-Edge-Suction Analogy Tech Library Kafb, Nm
    I A CONCEPT OF THE VORTEX LIFT OF SHARP-EDGE DELTA WINGS BASED ON A LEADING-EDGE-SUCTION ANALOGY TECH LIBRARY KAFB, NM OL3042b NASA TN D-3767 A CONCEPT OF THE VORTEX LIFT OF SHARP-EDGE DELTA WINGS BASED ON A LEADING-EDGE-SUCTION ANALOGY By Edward C. Polhamus Langley Research Center Langley Station, Hampton, Va. NATIONAL AERONAUTICS AND SPACE ADMINISTRATION For sale by the Clearinghouse for Federal Scientific and Technical Information Springfield, Virginia 22151 - Price $1.00 A CONCEPT OF THE VORTEX LIFT OF SHARP-EDGE DELTA WINGS BASED ON A LEADING-EDGE-SUCTION ANALOGY By Edward C. Polhamus Langley Research Center SUMMARY A concept for the calculation of the vortex lift of sharp-edge delta wings is pre­ sented and compared with experimental data. The concept is based on an analogy between the vortex lift and the leading-edge suction associated with the potential flow about the leading edge. This concept, when combined with potential-flow theory modified to include the nonlinearities associated with the exact boundary condition and the loss of the lift component of the leading-edge suction, provides excellent prediction of the total lift for a wide range of delta wings up to angles of attack of 20° or greater. INTRODUCTION The aerodynamic characteristics of thin sharp-edge delta wings are of interest for supersonic aircraft and have been the subject of theoretical and experimental studies for many years in both the subsonic and supersonic speed ranges. Of particular interest at subsonic speeds has been the formation and influence of the leading-edge separation vor­ tex that occurs on wings having sharp, highly swept leading edges.
    [Show full text]
  • Experimental Study on Turbulent Boundary-Layer Flows with Wall
    Experimental study on turbulent boundary-layer flows with wall transpiration by Marco Ferro October 2017 Technical Reports Royal Institute of Technology Department of Mechanics SE-100 44 Stockholm, Sweden Akademisk avhandling som med tillst˚andav Kungliga Tekniska H¨ogskolan i Stockholm framl¨agges till offentlig granskning f¨or avl¨aggande av teknologie doktorsexamen fredag den 24 November 2017 kl 10:15 i Kollegiesalen, Kungliga Tekniska H¨ogskolan, Brinellv¨agen 8, Stockholm. TRITA-MEK 2017:13 ISSN 0348-467X ISRN KTH/MEK/TR-17/13-SE ISBN 978-91-7729-556-3 c Marco Ferro 2017 Universitetsservice US{AB, Stockholm 2017 Experimental study on turbulent boundary-layer flows with wall transpiration Marco Ferro Linn´eFLOW Centre, KTH Mechanics, Royal Institute of Technology SE-100 44 Stockholm, Sweden Abstract Wall transpiration, in the form of wall-normal suction or blowing through a permeable wall, is a relatively simple and effective technique to control the be- haviour of a boundary layer. For its potential applications for laminar-turbulent transition and separation delay (suction) or for turbulent drag reduction and thermal protection (blowing), wall transpiration has over the past decades been the topic of a significant amount of studies. However, as far as the turbulent regime is concerned, fundamental understanding of the phenomena occurring in the boundary layer in presence of wall transpiration is limited and consid- erable disagreements persist even on the description of basic quantities, such as the mean streamwise velocity, for the rather simplified case of flat-plate boundary-layer flows without pressure gradients. In order to provide new experimental data on suction and blowing boundary layers, an experimental apparatus was designed and brought into operation.
    [Show full text]
  • Three Types of Horizontal Vortices Observed in Wildland Mass And
    1624 JOURNAL OF CLIMATE AND APPLIED METEOROLOGY VOLUME26 Three Types of Horizontal Vortices Observed in Wildland Mas~ and Crown Fires DoNALD A. HAINES U.S. Department ofAgriculture, Forest Service, North Central Forest Experiment Station, East Lansing, Ml 48823 MAHLON C. SMITH Department ofMechanical Engineering, Michigan State University, East Lansing, Ml 48824 (Manuscript received 25 October 1986, in final form 4 May 1987) ABSTRACT Observation shows that three types of horizontal vortices may form during intense wildland fires. Two of these vortices are longitudinal relative to the ambient wind and the third is transverse. One of the longitudinal types, a vortex pair, occurs with extreme heat and low to moderate wind speeds. It may be a somewhat common structure on the flanks of intense crown fires when burning is concentrated along the fire's perimeter. The second longitudinal type, a single vortex, occurs with high winds and can dominate the entire fire. The third type, the transverse vortex, occurs on the upstream side of the convection column during intense burning and relatively low winds. These vortices are important because they contribute to fire spread and are a threat to fire fighter safety. This paper documents field observations of the vortices and supplies supportive meteorological and fuel data. The discussion includes applicable laboratory and conceptual studies in fluid flow and heat transfer that may apply to vortex formation. 1. Introduction experiments showed that when air flowed parallel to a heated metal ribbon that simulated the flank of a crown The occurrence of vertical vortices in wildland fires fire, a thin, buoyant plume capped with a vortex pair has been well documented as well as mathematically developed above the ribbon along its length.
    [Show full text]
  • UNIT – 4 FORCES on IMMERSED BODIES Lecture-01
    1 UNIT – 4 FORCES ON IMMERSED BODIES Lecture-01 Forces on immersed bodies When a body is immersed in a real fluid, which is flowing at a uniform velocity U, the fluid will exert a force on the body. The total force (FR) can be resolved in two components: 1. Drag (FD): Component of the total force in the direction of motion of fluid. 2. Lift (FL): Component of the total force in the perpendicular direction of the motion of fluid. It occurs only when the axis of the body is inclined to the direction of fluid flow. If the axis of the body is parallel to the fluid flow, lift force will be zero. Expression for Drag & Lift Forces acting on the small elemental area dA are: i. Pressure force acting perpendicular to the surface i.e. p dA ii. Shear force acting along the tangential direction to the surface i.e. τ0dA (a) Drag force (FD) : Drag force on elemental area = p dAcosθ + τ0 dAcos(90 – θ = p dAosθ + τ0dAsinθ Hence Total drag (or profile drag) is given by, Where �� = ∫ � cos � �� + ∫�0 sin � �� = pressure drag or form drag, and ∫ � cos � �� = shear drag or friction drag or skin drag (b) Lift0 force (F ) : ∫ � sin � ��L Lift force on the elemental area = − p dAsinθ + τ0 dA sin(90 – θ = − p dAsiθ + τ0dAcosθ Hence, total lift is given by http://www.rgpvonline.com �� = ∫�0 cos � �� − ∫ p sin � �� 2 The drag & lift for a body moving in a fluid of density at a uniform velocity U are calculated mathematically as 2 � And �� = � � � 2 � Where A = projected area of the body or�� largest= � project� � area of the immersed body.
    [Show full text]
  • Effects of Wall Roughness on Adverse Pressure Gradient Boundary Layers
    Effects of Wall Roughness on Adverse Pressure Gradient Boundary Layers by Pouya Mottaghian A thesis submitted to the Department of Mechanical and Materials Engineering in conformity with the requirements for the degree of Master of Applied Science Queen's University Kingston, Ontario, Canada December, 2015 Copyright © Pouya Mottaghian, 2015 Abstract Large-eddy Simulations were carried out on a at-plate boundary layer over smooth and rough surfaces in the presence of an adverse pressure gradient, strong enough to induce separation. The inlet Reynolds number (based on freestream velocity and momentum thick- ness at the reference plane) is 2300. A sand-grain roughness model was implemented and spatial-resolution requirements were determined. Two roughness heights were used and a fully-rough ow condition is achieved at the refer- ence plane with roughness Reynolds numbers 60 and 120. As the friction velocity decreases due to the adverse pressure gradient the roughness Reynolds number varies from fully-rough to transitionally rough and smooth regime before the separation. The double-averaging approach illustrates how the roughness contribution decreases before the separation as the dispersive stresses decrease markedly compared to the upstream region. Before the ow detachment, roughness intensies the Reynolds stresses. After the sep- aration, the normal stresses, production and dissipation substantially increase through the adverse pressure gradient region. In the recovery region, the ow is highly three dimensional, as turbulent structures impinge on the wall at the reattachment region. Roughness initially increases the skin friction, then causes it to decrease faster than on a smooth wall, generating a considerably larger recirculation bubble for rough cases with earlier separation and later reattachment; increasing the wall roughness also leads to larger separation bubble.
    [Show full text]
  • 1 FLUID MECHANICS TUTORIAL No. 3 BOUNDARY LAYER THEORY In
    FLUID MECHANICS TUTORIAL No. 3 BOUNDARY LAYER THEORY In order to complete this tutorial you should already have completed tutorial 1 and 2 in this series. This tutorial examines boundary layer theory in some depth. When you have completed this tutorial, you should be able to do the following. Discuss the drag on bluff objects including long cylinders and spheres. Explain skin drag and form drag. Discuss the formation of wakes. Explain the concept of momentum thickness and displacement thickness. Solve problems involving laminar and turbulent boundary layers. Throughout there are worked examples, assignments and typical exam questions. You should complete each assignment in order so that you progress from one level of knowledge to another. Let us start by examining how drag is created on objects. 1 1. DRAG When a fluid flows around the outside of a body, it produces a force that tends to drag the body in the direction of the flow. The drag acting on a moving object such as a ship or an aeroplane must be overcome by the propulsion system. Drag takes two forms, skin friction drag and form drag. 1.1 SKIN FRICTION DRAG Skin friction drag is due to the viscous shearing that takes place between the surface and the layer of fluid immediately above it. This occurs on surfaces of objects that are long in the direction of flow compared to their height. Such bodies are called STREAMLINED. When a fluid flows over a solid surface, the layer next to the surface may become attached to it (it wets the surface).
    [Show full text]
  • Chapter 4: Immersed Body Flow [Pp
    MECH 3492 Fluid Mechanics and Applications Univ. of Manitoba Fall Term, 2017 Chapter 4: Immersed Body Flow [pp. 445-459 (8e), or 374-386 (9e)] Dr. Bing-Chen Wang Dept. of Mechanical Engineering Univ. of Manitoba, Winnipeg, MB, R3T 5V6 When a viscous fluid flow passes a solid body (fully-immersed in the fluid), the body experiences a net force, F, which can be decomposed into two components: a drag force F , which is parallel to the flow direction, and • D a lift force F , which is perpendicular to the flow direction. • L The drag coefficient CD and lift coefficient CL are defined as follows: FD FL CD = 1 2 and CL = 1 2 , (112) 2 ρU A 2 ρU Ap respectively. Here, U is the free-stream velocity, A is the “wetted area” (total surface area in contact with fluid), and Ap is the “planform area” (maximum projected area of an object such as a wing). In the remainder of this section, we focus our attention on the drag forces. As discussed previously, there are two types of drag forces acting on a solid body immersed in a viscous flow: friction drag (also called “viscous drag”), due to the wall friction shear stress exerted on the • surface of a solid body; pressure drag (also called “form drag”), due to the difference in the pressure exerted on the front • and rear surfaces of a solid body. The friction drag and pressure drag on a finite immersed body are defined as FD,vis = τwdA and FD, pres = pdA , (113) ZA ZA Streamwise component respectively.
    [Show full text]