COS 226 Lecture 18: Digraphs and Dags DIGRAPH: Directed Graph
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Applications of DFS
(b) acyclic (tree) iff a DFS yeilds no Back edges 2.A directed graph is acyclic iff a DFS yields no back edges, i.e., DAG (directed acyclic graph) , no back edges 3. Topological sort of a DAG { next 4. Connected components of a undirected graph (see Homework 6) 5. Strongly connected components of a drected graph (see Sec.22.5 of [CLRS,3rd ed.]) Applications of DFS 1. For a undirected graph, (a) a DFS produces only Tree and Back edges 1 / 7 2.A directed graph is acyclic iff a DFS yields no back edges, i.e., DAG (directed acyclic graph) , no back edges 3. Topological sort of a DAG { next 4. Connected components of a undirected graph (see Homework 6) 5. Strongly connected components of a drected graph (see Sec.22.5 of [CLRS,3rd ed.]) Applications of DFS 1. For a undirected graph, (a) a DFS produces only Tree and Back edges (b) acyclic (tree) iff a DFS yeilds no Back edges 1 / 7 3. Topological sort of a DAG { next 4. Connected components of a undirected graph (see Homework 6) 5. Strongly connected components of a drected graph (see Sec.22.5 of [CLRS,3rd ed.]) Applications of DFS 1. For a undirected graph, (a) a DFS produces only Tree and Back edges (b) acyclic (tree) iff a DFS yeilds no Back edges 2.A directed graph is acyclic iff a DFS yields no back edges, i.e., DAG (directed acyclic graph) , no back edges 1 / 7 4. Connected components of a undirected graph (see Homework 6) 5. -

9 the Graph Data Model
CHAPTER 9 ✦ ✦ ✦ ✦ The Graph Data Model A graph is, in a sense, nothing more than a binary relation. However, it has a powerful visualization as a set of points (called nodes) connected by lines (called edges) or by arrows (called arcs). In this regard, the graph is a generalization of the tree data model that we studied in Chapter 5. Like trees, graphs come in several forms: directed/undirected, and labeled/unlabeled. Also like trees, graphs are useful in a wide spectrum of problems such as com- puting distances, finding circularities in relationships, and determining connectiv- ities. We have already seen graphs used to represent the structure of programs in Chapter 2. Graphs were used in Chapter 7 to represent binary relations and to illustrate certain properties of relations, like commutativity. We shall see graphs used to represent automata in Chapter 10 and to represent electronic circuits in Chapter 13. Several other important applications of graphs are discussed in this chapter. ✦ ✦ ✦ ✦ 9.1 What This Chapter Is About The main topics of this chapter are ✦ The definitions concerning directed and undirected graphs (Sections 9.2 and 9.10). ✦ The two principal data structures for representing graphs: adjacency lists and adjacency matrices (Section 9.3). ✦ An algorithm and data structure for finding the connected components of an undirected graph (Section 9.4). ✦ A technique for finding minimal spanning trees (Section 9.5). ✦ A useful technique for exploring graphs, called “depth-first search” (Section 9.6). 451 452 THE GRAPH DATA MODEL ✦ Applications of depth-first search to test whether a directed graph has a cycle, to find a topological order for acyclic graphs, and to determine whether there is a path from one node to another (Section 9.7). -

A Low Complexity Topological Sorting Algorithm for Directed Acyclic Graph
International Journal of Machine Learning and Computing, Vol. 4, No. 2, April 2014 A Low Complexity Topological Sorting Algorithm for Directed Acyclic Graph Renkun Liu then return error (graph has at Abstract—In a Directed Acyclic Graph (DAG), vertex A and least one cycle) vertex B are connected by a directed edge AB which shows that else return L (a topologically A comes before B in the ordering. In this way, we can find a sorted order) sorting algorithm totally different from Kahn or DFS algorithms, the directed edge already tells us the order of the Because we need to check every vertex and every edge for nodes, so that it can simply be sorted by re-ordering the nodes the “start nodes”, then sorting will check everything over according to the edges from a Direction Matrix. No vertex is again, so the complexity is O(E+V). specifically chosen, which makes the complexity to be O*E. An alternative algorithm for topological sorting is based on Then we can get an algorithm that has much lower complexity than Kahn and DFS. At last, the implement of the algorithm by Depth-First Search (DFS) [2]. For this algorithm, edges point matlab script will be shown in the appendix part. in the opposite direction as the previous algorithm. The algorithm loops through each node of the graph, in an Index Terms—DAG, algorithm, complexity, matlab. arbitrary order, initiating a depth-first search that terminates when it hits any node that has already been visited since the beginning of the topological sort: I. -

CS302 Final Exam, December 5, 2016 - James S
CS302 Final Exam, December 5, 2016 - James S. Plank Question 1 For each of the following algorithms/activities, tell me its running time with big-O notation. Use the answer sheet, and simply circle the correct running time. If n is unspecified, assume the following: If a vector or string is involved, assume that n is the number of elements. If a graph is involved, assume that n is the number of nodes. If the number of edges is not specified, then assume that the graph has O(n2) edges. A: Sorting a vector of uniformly distributed random numbers with bucket sort. B: In a graph with exactly one cycle, determining if a given node is on the cycle, or not on the cycle. C: Determining the connected components of an undirected graph. D: Sorting a vector of uniformly distributed random numbers with insertion sort. E: Finding a minimum spanning tree of a graph using Prim's algorithm. F: Sorting a vector of uniformly distributed random numbers with quicksort (average case). G: Calculating Fib(n) using dynamic programming. H: Performing a topological sort on a directed acyclic graph. I: Finding a minimum spanning tree of a graph using Kruskal's algorithm. J: Finding the minimum cut of a graph, after you have found the network flow. K: Finding the first augmenting path in the Edmonds Karp implementation of network flow. L: Processing the residual graph in the Ford Fulkerson algorithm, once you have found an augmenting path. Question 2 Please answer the following statements as true or false. A: Kruskal's algorithm requires a starting node. -

Merkle Trees and Directed Acyclic Graphs (DAG) As We've Discussed, the Decentralized Web Depends on Linked Data Structures
Merkle trees and Directed Acyclic Graphs (DAG) As we've discussed, the decentralized web depends on linked data structures. Let's explore what those look like. Merkle trees A Merkle tree (or simple "hash tree") is a data structure in which every node is hashed. +--------+ | | +---------+ root +---------+ | | | | | +----+---+ | | | | +----v-----+ +-----v----+ +-----v----+ | | | | | | | node A | | node B | | node C | | | | | | | +----------+ +-----+----+ +-----+----+ | | +-----v----+ +-----v----+ | | | | | node D | | node E +-------+ | | | | | +----------+ +-----+----+ | | | +-----v----+ +----v-----+ | | | | | node F | | node G | | | | | +----------+ +----------+ In a Merkle tree, nodes point to other nodes by their content addresses (hashes). (Remember, when we run data through a cryptographic hash, we get back a "hash" or "content address" that we can think of as a link, so a Merkle tree is a collection of linked nodes.) As previously discussed, all content addresses are unique to the data they represent. In the graph above, node E contains a reference to the hash for node F and node G. This means that the content address (hash) of node E is unique to a node containing those addresses. Getting lost? Let's imagine this as a set of directories, or file folders. If we run directory E through our hashing algorithm while it contains subdirectories F and G, the content-derived hash we get back will include references to those two directories. If we remove directory G, it's like Grace removing that whisker from her kitten photo. Directory E doesn't have the same contents anymore, so it gets a new hash. As the tree above is built, the final content address (hash) of the root node is unique to a tree that contains every node all the way down this tree. -
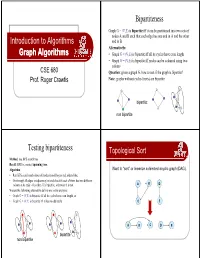
Graph Algorithms G
Bipartiteness Graph G = (V,E) is bipartite iff it can be partitioned into two sets of nodes A and B such that each edge has one end in A and the other Introduction to Algorithms end in B Alternatively: Graph Algorithms • Graph G = (V,E) is bipartite iff all its cycles have even length • Graph G = (V,E) is bipartite iff nodes can be coloured using two colours CSE 680 Question: given a graph G, how to test if the graph is bipartite? Prof. Roger Crawfis Note: graphs without cycles (trees) are bipartite bipartite: non bipartite Testing bipartiteness Toppgological Sort Method: use BFS search tree Recall: BFS is a rooted spanning tree. Algorithm: Want to “sort” or linearize a directed acyygp()clic graph (DAG). • Run BFS search and colour all nodes in odd layers red, others blue • Go through all edges in adjacency list and check if each of them has two different colours at its ends - if so then G is bipartite, otherwise it is not A B D We use the following alternative definitions in the analysis: • Graph G = (V,E) is bipartite iff all its cycles have even length, or • Graph G = (V, E) is bipartite iff it has no odd cycle C E A B C D E bipartit e non bipartite Toppgological Sort Example z PerformedonaPerformed on a DAG. A B D z Linear ordering of the vertices of G such that if 1/ (u, v) ∈ E, then u appears before v. Topological-Sort (G) 1. call DFS(G) to compute finishing times f [v] for all v ∈ V 2. -

6.042J Chapter 6: Directed Graphs
“mcs-ftl” — 2010/9/8 — 0:40 — page 189 — #195 6 Directed Graphs 6.1 Definitions So far, we have been working with graphs with undirected edges. A directed edge is an edge where the endpoints are distinguished—one is the head and one is the tail. In particular, a directed edge is specified as an ordered pair of vertices u, v and is denoted by .u; v/ or u v. In this case, u is the tail of the edge and v is the ! head. For example, see Figure 6.1. A graph with directed edges is called a directed graph or digraph. Definition 6.1.1. A directed graph G .V; E/ consists of a nonempty set of D nodes V and a set of directed edges E. Each edge e of E is specified by an ordered pair of vertices u; v V . A directed graph is simple if it has no loops (that is, edges 2 of the form u u) and no multiple edges. ! Since we will focus on the case of simple directed graphs in this chapter, we will generally omit the word simple when referring to them. Note that such a graph can contain an edge u v as well as the edge v u since these are different edges ! ! (for example, they have a different tail). Directed graphs arise in applications where the relationship represented by an edge is 1-way or asymmetric. Examples include: a 1-way street, one person likes another but the feeling is not necessarily reciprocated, a communication channel such as a cable modem that has more capacity for downloading than uploading, one entity is larger than another, and one job needs to be completed before another job can begin. -

Graph Algorithms
Graph Algorithms Graphs and Graph Repre- sentations Graph Graph Algorithms Traversals COMP4128 Programming Challenges Directed Graphs and Cycles Strongly Connected Components Example: School of Computer Science and Engineering 2SAT UNSW Australia Minimum Spanning Trees Table of Contents 2 Graph Algorithms 1 Graphs and Graph Representations Graphs and Graph Repre- sentations 2 Graph Graph Traversals Traversals Directed Graphs and 3 Directed Graphs and Cycles Cycles Strongly Connected 4 Strongly Connected Components Components Example: 2SAT 5 Example: 2SAT Minimum Spanning Trees 6 Minimum Spanning Trees Graphs 3 Graph Algorithms Graphs and Graph Repre- sentations A graph is a collection of vertices and edges connecting Graph pairs of vertices. Traversals Directed Generally, graphs can be thought of as abstract Graphs and Cycles representations of objects and connections between those Strongly objects, e.g. intersections and roads, people and Connected Components friendships, variables and equations. Example: Many unexpected problems can be solved with graph 2SAT techniques. Minimum Spanning Trees Graphs 4 Graph Algorithms Graphs and Graph Repre- sentations Graph Many different types of graphs Traversals Directed graphs Directed Graphs and Acyclic graphs, including trees Cycles Weighted graphs Strongly Connected Flow graphs Components Other labels for the vertices and edges Example: 2SAT Minimum Spanning Trees Graph Representations 5 Graph Algorithms Graphs and Graph Repre- sentations Graph You’ll usually want to either use an adjacency list or an Traversals adjacency matrix to store your graph. Directed Graphs and An adjacency matrix is just a table (usually implemented Cycles as an array) where the jth entry in the ith row represents Strongly Connected the edge from i to j, or lack thereof. -

The Shortest Path Problem with Edge Information Reuse Is NP-Complete
The Shortest Path Problem with Edge Information Reuse is NP-Complete Jesper Larsson Tr¨aff TU Wien Faculty of Informatics, Institute of Information Systems Research Group Parallel Computing Favoritenstrasse 16/184-5, 1040 Vienna, Austria email: [email protected] 15.9.2015, Revised 6.6.2016 Abstract We show that the following variation of the single-source shortest path problem is NP- complete. Let a weighted, directed, acyclic graph G = (V,E,w) with source and sink vertices s and t be given. Let in addition a mapping f on E be given that associates information with the edges (e.g., a pointer), such that f(e)= f(e′) means that edges e and e′ carry the same information; for such edges it is required that w(e)= w(e′). The length of a simple st path U is the sum of the weights of the edges on U but edges with f(e)= f(e′) are counted only once. The problem is to determine a shortest such st path. We call this problem the edge information reuse shortest path problem. It is NP-complete by reduction from 3SAT. 1 The Edge Information Reuse Shortest Path Problem A weighted, directed, acyclic graph G = (V, E, w) with source and sink vertices s,t ∈ V is given. Edges represent some possible substructures and a path from s to t determines how substructures are put together to form a desired superstructure. Edge weights reflect the cost of the associated substructures (e.g., memory consumption). An ordinary shortest path determines an ordered, tree-like representation of the superstructure of least cost: a single root with children given by the edges of the path. -
5 Directed Acyclic Graphs
5 Directed acyclic graphs (5.1) Introduction In many statistical studies we have prior knowledge about a temporal or causal ordering of the variables. In this chapter we will use directed graphs to incorporate such knowledge into a graphical model for the variables. Let XV = (Xv)v∈V be a vector of real-valued random variables with probability distribution P and density p. Then the density p can always be decomposed into a product of conditional densities, d Q p(x) = p(xd|x1, . , xd−1)p(x1, . , xd−1) = ... = p(xv|x1, . , xv−1). (5.1) v=1 Note that this can be achieved for any ordering of the variables. Now suppose that the conditional density of some variable Xv does not depend on all its predecessors, namely X1,...,Xv−1, but only on a subset XUv , that is, Xv is conditionally inde- pendent of its predecessors given XUv . Substituting p(xv|xUv ) for p(xv|x1, . , xv−1) in the product (5.1), we obtain d Q p(x) = p(xv|xUv ). (5.2) v=1 This recursive dependence structure can be represented by a directed graph G by drawing an arrow from each vertex in Uv to v. As an immediate consequence of the recursive factorization, the resulting graph is acyclic, that is, it does not contain any loops. On the other hand, P factorizes with respect to the undirected graph Gm which is given by the class of complete subsets D = {{v} ∪ Uv|v ∈ V }. This graph can be obtained from the directed graph G by completing all sets {v} ∪ Uv and then converting all directed edges into undirected ones. -
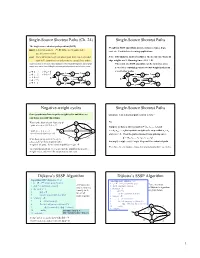
Single-Source Shortest Paths (Ch
Single-Source Shortest Paths (Ch. 24) Single-Source Shortest Paths The single-source shortest path problem (SSSP) Weights in SSSP algorithms include distances, times, hops, input: a directed graph G = (V, E) with edge weights, and a cost, etc. Used in lots of routing applications. specific source node s. goal: find a minimum weight (shortest) path from s to every other Note: BFS finds the shortest paths for the special case when all node in V (sometimes we only want the cost of these paths) edge weights are 1. Running time = O(V + E) It turns out that, in the worst case, finding the shortest path between s and a single The result of a SSSP algorithm can be viewed as a tree node t is no easier than finding the shortest paths between s and all other nodes rooted at s, containing a shortest (wrt weight) path from s à g = ¥ s to all other nodes. s à b = 2 2 3 s à c = 5 s à h = 7 a b c 2 3 5 6 a b 6 c s à d = 6 S 5 3 d 1 e S 3 s à e = 5 2 d 1 e 2 s à f = 3 f 4 g 2 h f 4 g 2 h 2 Negative-weight cycles Single-Source Shortest Paths Some graphs may have negative-weight cycles and these are Question: Can a shortest path contain a cycle? a problem for SSSP algorithms. What is the shortest path from a to d? No. b 9 · path a-c-e-d = -12+3-2 = -11 2 8 6 Suppose we have a shortest path p = áv0, v1, ..., vkñ and S -12 3 c = áv , v , ..., v ñ is a positive-weight cycle on p so that v = v · path a-c-e-d-a-c-e-d = a c e i i+1 j i j -12+3-2+(10-12+3-2)= -13 6 4 and w(c) > 0. -

Algorithms (Winter 2021) Ungraded Problem Set 5 Due: Not for Submission Topic: Graphs: Basics + DFS
CS 31: Algorithms (Winter 2021) Ungraded Problem Set 5 Due: Not for submission Topic: Graphs: Basics + DFS Problem 1 (Some operations with graphs). For the parts below, describe your algorithm summary in English and also provide a clear pseudocode. You may assume the graph G = (V; E) is input as adjacency lists. a. In this part the graph G is directed. You need to return the reverse graph Grev where all edges have been reversed. Grev should also be represented as adjacency lists. What is the runtime of your algo- rithm? K b. Recall the definition of a walk from vertex u to vertex v and a path from vertex u to v. Design an algorithm which takes input a walk from u to v, and returns a path from u to v. K Problem 2 (DFS firsts and lasts). For each of the following assertions, prove or give a counterexample. The graph G, unless mentioned, is directed. When you give a counter-example, you should explain why it is a counter-example. (a) If G contains a path from u to v and if first[u] < first[v] in a depth-first search of G, then last[v] < last[u]. K (b) If (u=v1; v2; : : : ; vk =v) is a path from u to v in G such that last[vi] < last[v] for all 1 ≤ i < k, then first[v] < first[vi] for all 1 ≤ i < k. K (c) If we run depth-first search on G in an arbitrary order to obtain first’s and last’s, and let σ be the increasing order of last[v]’s.