High-Thrust Interplanetary Spacecraft Trajectory Optimization Using Cuda
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Astrodynamics
Politecnico di Torino SEEDS SpacE Exploration and Development Systems Astrodynamics II Edition 2006 - 07 - Ver. 2.0.1 Author: Guido Colasurdo Dipartimento di Energetica Teacher: Giulio Avanzini Dipartimento di Ingegneria Aeronautica e Spaziale e-mail: [email protected] Contents 1 Two–Body Orbital Mechanics 1 1.1 BirthofAstrodynamics: Kepler’sLaws. ......... 1 1.2 Newton’sLawsofMotion ............................ ... 2 1.3 Newton’s Law of Universal Gravitation . ......... 3 1.4 The n–BodyProblem ................................. 4 1.5 Equation of Motion in the Two-Body Problem . ....... 5 1.6 PotentialEnergy ................................. ... 6 1.7 ConstantsoftheMotion . .. .. .. .. .. .. .. .. .... 7 1.8 TrajectoryEquation .............................. .... 8 1.9 ConicSections ................................... 8 1.10 Relating Energy and Semi-major Axis . ........ 9 2 Two-Dimensional Analysis of Motion 11 2.1 ReferenceFrames................................. 11 2.2 Velocity and acceleration components . ......... 12 2.3 First-Order Scalar Equations of Motion . ......... 12 2.4 PerifocalReferenceFrame . ...... 13 2.5 FlightPathAngle ................................. 14 2.6 EllipticalOrbits................................ ..... 15 2.6.1 Geometry of an Elliptical Orbit . ..... 15 2.6.2 Period of an Elliptical Orbit . ..... 16 2.7 Time–of–Flight on the Elliptical Orbit . .......... 16 2.8 Extensiontohyperbolaandparabola. ........ 18 2.9 Circular and Escape Velocity, Hyperbolic Excess Speed . .............. 18 2.10 CosmicVelocities -
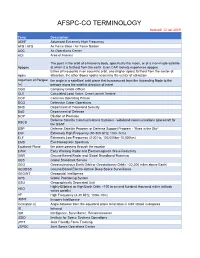
AFSPC-CO TERMINOLOGY Revised: 12 Jan 2019
AFSPC-CO TERMINOLOGY Revised: 12 Jan 2019 Term Description AEHF Advanced Extremely High Frequency AFB / AFS Air Force Base / Air Force Station AOC Air Operations Center AOI Area of Interest The point in the orbit of a heavenly body, specifically the moon, or of a man-made satellite Apogee at which it is farthest from the earth. Even CAP rockets experience apogee. Either of two points in an eccentric orbit, one (higher apsis) farthest from the center of Apsis attraction, the other (lower apsis) nearest to the center of attraction Argument of Perigee the angle in a satellites' orbit plane that is measured from the Ascending Node to the (ω) perigee along the satellite direction of travel CGO Company Grade Officer CLV Calculated Load Value, Crew Launch Vehicle COP Common Operating Picture DCO Defensive Cyber Operations DHS Department of Homeland Security DoD Department of Defense DOP Dilution of Precision Defense Satellite Communications Systems - wideband communications spacecraft for DSCS the USAF DSP Defense Satellite Program or Defense Support Program - "Eyes in the Sky" EHF Extremely High Frequency (30-300 GHz; 1mm-1cm) ELF Extremely Low Frequency (3-30 Hz; 100,000km-10,000km) EMS Electromagnetic Spectrum Equitorial Plane the plane passing through the equator EWR Early Warning Radar and Electromagnetic Wave Resistivity GBR Ground-Based Radar and Global Broadband Roaming GBS Global Broadcast Service GEO Geosynchronous Earth Orbit or Geostationary Orbit ( ~22,300 miles above Earth) GEODSS Ground-Based Electro-Optical Deep Space Surveillance -

Asteroid Retrieval Mission
Where you can put your asteroid Nathan Strange, Damon Landau, and ARRM team NASA/JPL-CalTech © 2014 California Institute of Technology. Government sponsorship acknowledged. Distant Retrograde Orbits Works for Earth, Moon, Mars, Phobos, Deimos etc… very stable orbits Other Lunar Storage Orbit Options • Lagrange Points – Earth-Moon L1/L2 • Unstable; this instability enables many interesting low-energy transfers but vehicles require active station keeping to stay in vicinity of L1/L2 – Earth-Moon L4/L5 • Some orbits in this region is may be stable, but are difficult for MPCV to reach • Lunar Weakly Captured Orbits – These are the transition from high lunar orbits to Lagrange point orbits – They are a new and less well understood class of orbits that could be long term stable and could be easier for the MPCV to reach than DROs – More study is needed to determine if these are good options • Intermittent Capture – Weakly captured Earth orbit, escapes and is then recaptured a year later • Earth Orbit with Lunar Gravity Assists – Many options with Earth-Moon gravity assist tours Backflip Orbits • A backflip orbit is two flybys half a rev apart • Could be done with the Moon, Earth or Mars. Backflip orbit • Lunar backflips are nice plane because they could be used to “catch and release” asteroids • Earth backflips are nice orbits in which to construct things out of asteroids before sending them on to places like Earth- Earth or Moon orbit plane Mars cyclers 4 Example Mars Cyclers Two-Synodic-Period Cycler Three-Synodic-Period Cycler Possibly Ballistic Chen, et al., “Powered Earth-Mars Cycler with Three Synodic-Period Repeat Time,” Journal of Spacecraft and Rockets, Sept.-Oct. -

An Examination of the Mass Limit for Stability at the Triangular Lagrange
San Jose State University SJSU ScholarWorks Master's Theses Master's Theses and Graduate Research Spring 2015 An Examination of the Mass Limit for Stability at the Triangular Lagrange Points for a Three-Body System and a Special Case of the Four-Body Problem Sean Kemp San Jose State University Follow this and additional works at: https://scholarworks.sjsu.edu/etd_theses Recommended Citation Kemp, Sean, "An Examination of the Mass Limit for Stability at the Triangular Lagrange Points for a Three-Body System and a Special Case of the Four-Body Problem" (2015). Master's Theses. 4546. DOI: https://doi.org/10.31979/etd.4tf8-hnqx https://scholarworks.sjsu.edu/etd_theses/4546 This Thesis is brought to you for free and open access by the Master's Theses and Graduate Research at SJSU ScholarWorks. It has been accepted for inclusion in Master's Theses by an authorized administrator of SJSU ScholarWorks. For more information, please contact [email protected]. AN EXAMINATION OF THE MASS LIMIT FOR STABILITY AT THE TRIANGULAR LAGRANGE POINTS FOR A THREE-BODY SYSTEM AND A SPECIAL CASE OF THE FOUR-BODY PROBLEM A Thesis Presented to The Faculty of the Department of Physics and Astronomy San José State University In Partial Fulllment of the Requirements for the Degree Master of Science by Sean P. Kemp May 2015 c 2015 Sean P. Kemp ALL RIGHTS RESERVED The Designated Thesis Committee Approves the Thesis Titled AN EXAMINATION OF THE MASS LIMIT FOR STABILITY AT THE TRIANGULAR LAGRANGE POINTS FOR A THREE-BODY SYSTEM AND A SPECIAL CASE OF THE FOUR-BODY PROBLEM by Sean P. -

Design of Small Circular Halo Orbit Around L2
Design of Small Circular Halo Orbit around L2 Kohta Tarao* and Jun’ichiro Kawaguchi** *Graduate Student, Department of Aeronautics and Astronautics, School of Engineering, The University of Tokyo ** The Institute of Space and Astronautics Science / Japan Aerospace Exploration Agency (ISAS/JAXA) 3-1-1 Yoshinodai, Sagamihara, Kanagawa 229-8510, JAPAN. Abstract A Lagrange point of Sun-Earth system, L1 or L2 is conceived one of the best point for astronomy and connection ports for outer planets. This paper describes a new useful control method for realizing and keeping small circular Halo orbits around the L2 point. First, a control law is mathematically derived from the restricted three body problem formulation and the associated properties are discussed. And next, some useful cases for the space mission are verified numerically using real ephemeris. The resulted Halo orbit is compact and circular realized with satisfactorily small thrust. The paper concludes the strategy is applied to many kinds of missions. L2 点周りの小円ハロー軌道設計 多羅尾康太(東大・工・院)、川口淳一郎(ISAS/JAXA) 摘要 太陽―月・地球系におけるラグランジュ点の中で、L2 点は太陽と地球との距離がほぼ一定で、太 陽、地球との幾何学的関係が保たれ、またダウンリンク通信が太陽の影響を受けない点で L1 点よ りも有利である。そのため L2 点周辺の軌道は、赤外線天文衛星や外惑星探査のための起・終点と しての宇宙港の軌道として利用が考えられている。本論文では、新しい制御法により L2 点回りに 小さな円形の Halo 軌道が作れることを示す。まず初めに、円制限三体問題における線形化された 方程式から理論的に制御則を導く。その後、実軌道要素を用いて軌道制御方法を検証する。軌道制 御に必要な推力は十分小さく大変実用的な制御方法である。 INTRODUCTION million kilometers and also due to its highly alternating geometry. A Lissajous orbit also exists A Lagrange point is the point where the gravity of around the L2 point naturally, however, the orbital two planets such as Sun and Earth is equal to plane rotates and the solar power availability is centrifugal force by their circular motions. L1 and often restricted due to the shadow by the Earth. -

Stability of the Lagrange Points, L4 and L5
Stability of the Lagrange Points, L4 and L5 Thomas Greenspan January 7, 2014 Abstract A proof of the stability of the non collinear Lagrange Points, L4 and L5. We will start by covering the basics of stability, stating a theorem (without proof) with a few corollaries, and then turn to the Lagrange points, proving first the stability of all Lagrange points in the z-direction and then restricting our attention to the the points, L4 and L5. Introduction The three body problem is one that has been studied for many centuries. It consists of considering 3 bodies, subject to only to mutually attracting forces (determined by the inverse square force, gravitation) and to solve for the motions of the three bodies. This task can be extremely complicated and, following Poincar´e's example, most mathematicians and physicists have interested themselves in the finding periodic solutions to the problem, that is, where x(t) = x(t + T ) where T is the period [3]. Indeed not only does this offer a useful framework from within which to work, but also describes states that are most applicable and useful to real world situations. Finding these periodic solutions is by no means trivial. It is a problem that has been worked on for centuries and still is in modern times, one of the latest publications dealing with it as recent as March of 2013 [9]. Among the first to interest themselves in and find solutions to the 3 body problem were Leonhard Euler in 1765 and Joseph Lagrange in 1772 [3]. In his publication, Essai sur le probl`emedes trois corps (Essay on the 3-Body Problem), Lagrange proposed a method that had never been used until then, that of considering only the distances between the three bodies rather than their absolute positions [2]. -

Rideshare and the Orbital Maneuvering Vehicle: the Key to Low-Cost Lagrange-Point Missions
SSC15-II-5 Rideshare and the Orbital Maneuvering Vehicle: the Key to Low-cost Lagrange-point Missions Chris Pearson, Marissa Stender, Christopher Loghry, Joe Maly, Valentin Ivanitski Moog Integrated Systems 1113 Washington Avenue, Suite 300, Golden, CO, 80401; 303 216 9777, extension 204 [email protected] Mina Cappuccio, Darin Foreman, Ken Galal, David Mauro NASA Ames Research Center PO Box 1000, M/S 213-4, Moffett Field, CA 94035-1000; 650 604 1313 [email protected] Keats Wilkie, Paul Speth, Trevor Jackson, Will Scott NASA Langley Research Center 4 West Taylor Street, Mail Stop 230, Hampton, VA, 23681; 757 864 420 [email protected] ABSTRACT Rideshare is a well proven approach, in both LEO and GEO, enabling low-cost space access through splitting of launch charges between multiple passengers. Demand exists from users to operate payloads at Lagrange points, but a lack of regular rides results in a deficiency in rideshare opportunities. As a result, such mission architectures currently rely on a costly dedicated launch. NASA and Moog have jointly studied the technical feasibility, risk and cost of using an Orbital Maneuvering Vehicle (OMV) to offer Lagrange point rideshare opportunities. This OMV would be launched as a secondary passenger on a commercial rocket into Geostationary Transfer Orbit (GTO) and utilize the Moog ESPA secondary launch adapter. The OMV is effectively a free flying spacecraft comprising a full suite of avionics and a propulsion system capable of performing GTO to Lagrange point transfer via a weak stability boundary orbit. In addition to traditional OMV ’tug’ functionality, scenarios using the OMV to host payloads for operation at the Lagrange points have also been analyzed. -

Stability of Lagrange Points: James Webb Space Telescope
Stability of Lagrange Points: James Webb Space Telescope Cacolici, Gianna Nicole; Hanson, Jake; Lejoly, Cassandra; Pearson, Kyle Alexander; Reynolds, Katherine ABSTRACT We continue to present a detailed procedure for analyzing the stability of Lagrange points both analytically and computationally. We verified the stability both analytically in a 2D EarthSun system, and computationally with a 3D Nbody code. We tested the stability over several periods of time and plotted the path the orbits would take in such case. We also discuss the consequences of these stabilities with respect to the James Webb Space Telescope. I. INTRODUCTION Astronomy has been as a subject studied by humans for a few thousands of years. One of the most fascinating parts of astronomy is the study of the retrograde motion of the planets in the sky. Among the earliest recorded studies of the motion of planets was by Ptolemy around the year 150 CE (Jones). Ptolemy’s geocentric model of the universe was accepted for many centuries following his death. This model placed the Earth at the center of the universe with the Sun and planets rotating around the Earth in epicycles. It was not until Copernicus came along (14731543) that the idea of a heliocentric system came along. He believed that the size of the planets’ orbits was proportional to the distance from the Sun (Rabin 2004). This model, which features the Sun in the center and the planets rotating around it, was not accepted initially, but became the accepted belief of the universe. It was not long until the telescope was invented and people started to truly record the motion of the planets. -

A Preliminary Study of Leo to Geo Transfers for Inclination Changes Using Libration Point Orbits
University of North Dakota UND Scholarly Commons Theses and Dissertations Theses, Dissertations, and Senior Projects January 2020 A Preliminary Study Of Leo To Geo Transfers For Inclination Changes Using Libration Point Orbits John Shepard Follow this and additional works at: https://commons.und.edu/theses Recommended Citation Shepard, John, "A Preliminary Study Of Leo To Geo Transfers For Inclination Changes Using Libration Point Orbits" (2020). Theses and Dissertations. 3121. https://commons.und.edu/theses/3121 This Thesis is brought to you for free and open access by the Theses, Dissertations, and Senior Projects at UND Scholarly Commons. It has been accepted for inclusion in Theses and Dissertations by an authorized administrator of UND Scholarly Commons. For more information, please contact [email protected]. A PRELIMINARY STUDY OF LEO TO GEO TRANSFERS FOR INCLINATION CHANGES USING LIBRATION POINT ORBITS by John Philip Shepard Applied Associates of Science, Community College of the Air Force, 2012 Applied Associates of Science, Community College of the Air Force, 2019 Bachelor of Science, Chadron State College, 2012 A Thesis . Submitted to the Graduate Faculty of the University of North Dakota in partial fulfillment of the requirements for the degree of Master of Science Grand Forks, North Dakota May 2020 iii This thesis , submitted by John Shepard in partial fulfillment of the requirement for the Degree of Master of Science in Space Studies from the University of North Dakota, has been read by the Faculty Advisory Committee under whom the work has been done and is hereby approved. This thesis is being submitted by the appointed advisory committee as having met all of the requirements of the school of Graduate Studies at the University of North Dakota and is hereby approved. -

Orbital Stability Zones About Asteroids
ICARUS 92, 118-131 (1991) Orbital Stability Zones about Asteroids DOUGLAS P. HAMILTON AND JOSEPH A. BURNS Cornell University, Ithaca, New York, 14853-6801 Received October 5, 1990; revised March 1, 1991 exploration program should be remedied when the Galileo We have numerically investigated a three-body problem con- spacecraft, launched in October 1989, encounters the as- sisting of the Sun, an asteroid, and an infinitesimal particle initially teroid 951 Gaspra on October 29, 1991. It is expected placed about the asteroid. We assume that the asteroid has the that the asteroid's surroundings will be almost devoid of following properties: a circular heliocentric orbit at R -- 2.55 AU, material and therefore benign since, in the analogous case an asteroid/Sun mass ratio of/~ -- 5 x 10-12, and a spherical of the satellites of the giant planets, significant debris has shape with radius R A -- 100 km; these values are close to those of never been detected. The analogy is imperfect, however, the minor planet 29 Amphitrite. In order to describe the zone in and so the possibility that interplanetary debris may be which circum-asteroidal debris could be stably trapped, we pay particular attention to the orbits of particles that are on the verge enhanced in the gravitational well of the asteroid must be of escape. We consider particles to be stable or trapped if they considered. If this is the case, the danger of collision with remain in the asteroid's vicinity for at least 5 asteroid orbits about orbiting debris may increase as the asteroid is approached. -

Three-Body Capture of Irregular Satellites: Application to Jupiter
Icarus 208 (2010) 824–836 Contents lists available at ScienceDirect Icarus journal homepage: www.elsevier.com/locate/icarus Three-body capture of irregular satellites: Application to Jupiter Catherine M. Philpott a,*, Douglas P. Hamilton a, Craig B. Agnor b a Department of Astronomy, University of Maryland, College Park, MD 20742-2421, USA b Astronomy Unit, School of Mathematical Sciences, Queen Mary University of London, London E14NS, UK article info abstract Article history: We investigate a new theory of the origin of the irregular satellites of the giant planets: capture of one Received 19 October 2009 member of a 100-km binary asteroid after tidal disruption. The energy loss from disruption is sufficient Revised 24 March 2010 for capture, but it cannot deliver the bodies directly to the observed orbits of the irregular satellites. Accepted 26 March 2010 Instead, the long-lived capture orbits subsequently evolve inward due to interactions with a tenuous cir- Available online 7 April 2010 cumplanetary gas disk. We focus on the capture by Jupiter, which, due to its large mass, provides a stringent test of our model. Keywords: We investigate the possible fates of disrupted bodies, the differences between prograde and retrograde Irregular satellites captures, and the effects of Callisto on captured objects. We make an impulse approximation and discuss Jupiter, Satellites Planetary dynamics how it allows us to generalize capture results from equal-mass binaries to binaries with arbitrary mass Satellites, Dynamics ratios. Jupiter We find that at Jupiter, binaries offer an increase of a factor of 10 in the capture rate of 100-km objects as compared to single bodies, for objects separated by tens of radii that approach the planet on relatively low-energy trajectories. -

Satellite Capture Mechanism in a Sun-Planet-Binary Four-Body System
Satellite capture mechanism in a sun-planet-binary four-body system Shengping Gong*, Miao Li † School of Aerospace Engineering, Tsinghua University, Beijing China, 100084 Abstract This paper studies the binary disruption problem and asteroid capture mechanism in a sun-planet-binary four-body system. Firstly, the binary disruption condition is studied and the result shows that the binary is always disrupted at the perigee of their orbit instantaneously. Secondly, an analytic expression to describe the energy exchange between the binary is derived based on the ‘instantaneous disruption’ hypothesis. The analytic result is validated through numerical integration. We obtain the energy exchange in encounters simultaneously by the analytic expression and numerical integration. The maximum deviation of this two results is always less than 25% and the mean deviation is about 8.69%. The analytic expression can give us an intuitive description of the energy exchange between the binary. It indicates that the energy change depends on the hyperbolic shape of the binary orbit with respect to the planet, the masses of planet and the primary member of the binary, the binary phase at perigee. We can illustrate the capture/escape processes and give the capture/escape region of the binary clearly by numerical simulation. We analyse the influence of some critical *Associate professor, School of Aerospace Engineering; [email protected] † PhD candidate, School of Aerospace Engineering; [email protected] 1 factors to the capture region finally. Key words: binary; capture mechanism; disruption; analytic derivation; numerical results 1 Introduction In the last decade, hundreds of irregular satellites orbiting giant planets have been found in our solar system.