Hockey Player Performance Via Regularized Logistic Regression
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Head Coach, Tampa Bay Lightning
Table of Contents ADMINISTRATION Team History 270 - 271 All-Time Individual Record 272 - 274 Company Directory 4 - 5 All-Time Team Records 274 - 279 Executives 6 - 11 Scouting Staff 11 - 12 Coaching Staff 13 - 16 PLAYOFF HISTORY & RECORDS Hockey Operations 17 - 20 All-Time Playoff Scoring 282 Broadcast 21 - 22 Playoff Firsts 283 All-Time Playoff Results 284 - 285 2013-14 PLAYER ROSTER Team Playoff Records 286 - 287 Individual Playoff Records 288 - 289 2013-14 Player Roster 23 - 98 Minor League Affiliates 99 - 100 MISCELLANEOUS NHL OPPONENTS In the Community 292 NHL Executives 293 NHL Opponents 109 - 160 NHL Officials and Referees 294 Terms Glossary 295 2013-14 SEASON IN REVIEW Medical Glossary 296 - 298 Broadcast Schedule 299 Final Standings, Individual Leaders, Award Winners 170 - 172 Media Regulations and Policies 300 - 301 Team Statistics, Game-by-Game Results 174 - 175 Frequently Asked Questions 302 - 303 Home and Away Results 190 - 191 Season Summary, Special Teams, Overtime/Shootout 176 - 178 Highs and Lows, Injuries 179 Win / Loss Record 180 HISTORY & RECORDS Season Records 182 - 183 Special Teams 184 Season Leaders 185 All-Time Records 186 - 187 Last Trade With 188 Records vs. Opponents 189 Overtime/Shootout Register 190 - 191 Overtime History 192 Year by Year Streaks 193 All-Time Hat Tricks 194 All-Time Attendance 195 All-Time Shootouts & Penalty Shots 196-197 Best and Worst Record 198 Season Openers and Closers 199 - 201 Year by Year Individual Statistics and Game Results 202 - 243 All-Time Lightning Preseason Results 244 All-Time -

Inside This Issue…
Tuesday November 16, 2010 Issue 1, Page 1 “Do not go where the path may lead, go instead where there is no path and leave a trail” – Ralph Waldo Emerson Inside this Issue… News & Events………………………………………………….….………………………2 Calendar………………………………………………….…………………………………….2 Sports………………………………………………………………….………….…………….3 Entertainment……………………………………………….………………………………4 Opinions & Info ……………………………………………………….…………………..6 Clubs……………………………………………………………………………………………..7 Issue 1, Page 2 NEWS & EVENTS Halloween Vanessa Yang As a grade 9 student, I’m a new comer of the When I walked into the classrooms, students school. This year, I just experienced my first Halloween were distracted by the teachers’ new fresh looks. in Pinetree Secondary. On Friday, October 29 th, Teachers too, were in costumes that were very unique. everyone in Pinetree Secondary School dressed up in These costumes showed their interests in different areas costumes. As I walked down the hallway, looked at the of studies. Some students claimed that the teachers can different kinds of disguises, I felt truly excited. Students look very nice in their costumes, and that a change like eagerly showed their special and amazing styles, and this is good once in a while. Some grade 9 students even different tastes in costumes. People showed up as said that they think the teachers should wear costumes werewolves, witches, vampires, and so many other more often, because they looked amazing in them. legendary characters. Girls pretended to be maids, and Everybody was happy and satisfied because of some even had a tea pot with them; guys pretended to this special day. Friday is now over, but I believe that we be ghosts and monsters, and some painted their will all remember the great Halloween we had this year! mouths with fake blood. -

36 Conference Championships
36 Conference Championships - 21 Regular Season, 15 Tournament TERRIERS IN THE NHL DRAFT Name Team Year Round Pick Clayton Keller Arizona Coyotes 2016 1 7 Since 1969, 163 players who have donned the scarlet Charlie McAvoy Boston Bruins 2016 1 14 and white Boston University sweater have been drafted Dante Fabbro Nashville Predators 2016 1 17 by National Hockey League organizations. The Terriers Kieffer Bellows New York Islanders 2016 1 19 have had the third-largest number of draftees of any Chad Krys Chicago Blackhawks 2016 2 45 Patrick Harper Nashville Predators 2016 5 138 school, trailing only Minnesota and Michigan. The Jack Eichel Buffalo Sabres 2015 1 2 number drafted is the most of any Hockey East school. A.J. Greer Colorado Avalanche 2015 2 39 Jakob Forsbacka Karlsson Boston Bruins 2015 2 45 Fifteen Terriers have been drafted in the first round. Jordan Greenway Minnesota Wild 2015 2 50 Included in this list is Rick DiPietro, who played for John MacLeod Tampa Bay Lightning 2014 2 57 Brandon Hickey Calgary Flames 2014 3 64 the Terriers during the 1999-00 season. In the 2000 J.J. Piccinich Toronto Maple Leafs 2014 4 103 draft, DiPietro became the first goalie ever selected Sam Kurker St. Louis Blues 2012 2 56 as the number one overall pick when the New York Matt Grzelcyk Boston Bruins 2012 3 85 Islanders made him their top choice. Sean Maguire Pittsburgh Penguins 2012 4 113 Doyle Somerby New York Islanders 2012 5 125 Robbie Baillargeon Ottawa Senators 2012 5 136 In the 2015 Entry Draft, Jack Eichel was selected Danny O’Regan San Jose Sharks 2012 5 138 second overall by the Buffalo Sabres. -

Anaheim Ducks Game Notes
Anaheim Ducks Game Notes Fri, Nov 8, 2013 NHL Game #244 Anaheim Ducks 13 - 3 - 1 (27 pts) Buffalo Sabres 3 - 14 - 1 (7 pts) Team Game: 18 6 - 0 - 0 (Home) Team Game: 19 0 - 8 - 1 (Home) Home Game: 7 7 - 3 - 1 (Road) Road Game: 10 3 - 6 - 0 (Road) # Goalie GP W L OT GAA SV% # Goalie GP W L OT GAA SV% 1 Jonas Hiller 11 7 2 1 2.47 .908 1 Jhonas Enroth 6 1 4 1 2.84 .911 31 Frederik Andersen 4 4 0 0 1.36 .952 30 Ryan Miller 12 2 10 0 3.09 .919 # P Player GP G A P +/- PIM # P Player GP G A P +/- PIM 4 D Cam Fowler 17 1 6 7 0 2 3 D Mark Pysyk 18 0 2 2 -4 4 5 D Luca Sbisa 2 0 1 1 0 10 4 D Jamie McBain 10 1 3 4 -4 2 6 D Ben Lovejoy 16 0 1 1 6 4 8 C Cody McCormick 14 1 2 3 -3 32 7 C Andrew Cogliano 17 3 4 7 5 8 9 C Steve Ott (C) 18 2 2 4 -7 26 8 R Teemu Selanne (A) 12 3 4 7 0 0 10 D Christian Ehrhoff (A) 18 0 4 4 -3 4 10 R Corey Perry 17 10 7 17 10 16 19 C Cody Hodgson 18 5 8 13 -6 4 13 C Nick Bonino 17 4 6 10 4 6 20 D Henrik Tallinder 13 2 1 3 -4 14 15 C Ryan Getzlaf (C) 17 7 11 18 9 13 21 R Drew Stafford 18 2 3 5 -4 6 17 L Dustin Penner 10 2 6 8 15 2 22 L Johan Larsson 16 0 1 1 -1 13 21 R Kyle Palmieri 15 4 2 6 0 9 23 L Ville Leino 7 0 1 1 -2 2 22 C Mathieu Perreault 16 5 9 14 10 6 25 C Mikhail Grigorenko 13 0 1 1 -3 2 23 D Francois Beauchemin 17 0 4 4 13 15 26 L Matt Moulson 16 8 7 15 1 6 28 D Mark Fistric 3 0 1 1 0 6 28 C Zemgus Girgensons 17 1 4 5 0 2 34 C Daniel Winnik 17 1 4 5 -1 8 32 L John Scott 7 0 0 0 -3 19 45 D Sami Vatanen 15 1 4 5 3 6 55 D Rasmus Ristolainen 15 1 0 1 -5 4 47 D Hampus Lindholm 15 1 4 5 13 6 57 D Tyler Myers 18 1 3 4 -7 31 55 D Bryan Allen 17 0 5 5 10 21 61 D Nikita Zadorov 6 1 0 1 -3 2 62 L Patrick Maroon 13 2 2 4 4 17 63 C Tyler Ennis 18 2 3 5 -6 8 65 R Emerson Etem 14 4 2 6 3 2 65 C Brian Flynn 18 2 1 3 -3 0 67 C Rickard Rakell 2 0 0 0 1 0 78 R Corey Tropp 3 0 0 0 -4 0 77 R Devante Smith-Pelly 8 1 5 6 7 0 82 L Marcus Foligno 15 2 4 6 -6 18 Exec. -

Canucks Centre for Bc Hockey
1 | Coaching Day in BC MANUAL CONTENT AGENDA……………………….………………………………………………………….. 4 WELCOME MESSAGE FROM TOM RENNEY…………….…………………………. 6 COACHING DAY HISTORY……………………………………………………………. 7 CANUCKS CENTRE FOR BC HOCKEY……………………………………………… 8 CANUCKS FOR KIDS FUND…………………………………………………………… 10 BC HOCKEY……………………………………………………………………………… 15 ON-ICE SESSION………………………………………………………………………. 20 ON-ICE COURSE CONDUCTORS……………………………………………. 21 ON-ICE DRILLS…………………………………………………………………. 22 GOALTENDING………………………………………………………………………….. 23 PASCO VALANA- ELITE GOALIES………………………………………… GOALTENDING DRILLS…………………………………….……………..… CANUCKS COACHES & PRACTICE…………………………………………………… 27 PROSMART HOCKEY LEARNING SYSTEM ………………………………………… 32 ADDITIONAL COACHING RESOURCES………………………………………….….. 34 SPORTS NUTRITION ………………………….……………………………….. PRACTICE PLANS………………………………………………………………… 2 | Coaching Day in BC The Timbits Minor Sports Program began in 1982 and is a community-oriented sponsorship program that provides opportunities for kids aged four to nine to play house league sports. The philosophy of the program is based on learning a new sport, making new friends, and just being a kid, with the first goal of all Timbits Minor Sports Programs being to have fun. Over the last 10 years, Tim Hortons has invested more than $38 million in Timbits Minor Sports (including Hockey, Soccer, Baseball and more), which has provided sponsorship to more than three million children across Canada, and more than 50 million hours of extracurricular activity. In 2016 alone, Tim Hortons will invest $7 million in Timbits Minor -
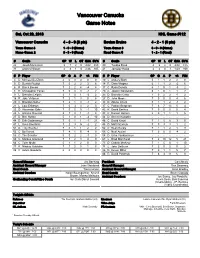
Vancouver Canucks Game Notes
Vancouver Canucks Game Notes Sat, Oct 20, 2018 NHL Game #112 Vancouver Canucks 4 - 3 - 0 (8 pts) Boston Bruins 4 - 2 - 1 (9 pts) Team Game: 8 1 - 0 - 0 (Home) Team Game: 8 3 - 0 - 0 (Home) Home Game: 2 3 - 3 - 0 (Road) Road Game: 5 1 - 2 - 1 (Road) # Goalie GP W L OT GAA SV% # Goalie GP W L OT GAA SV% 25 Jacob Markstrom 3 1 2 0 4.02 .883 40 Tuukka Rask 4 2 2 0 4.08 .875 31 Anders Nilsson 4 3 1 0 2.26 .925 41 Jaroslav Halak 4 2 0 1 1.69 .939 # P Player GP G A P +/- PIM # P Player GP G A P +/- PIM 4 D Michael Del Zotto 2 0 0 0 0 0 10 L Anders Bjork 5 1 1 2 2 0 5 D Derrick Pouliot 7 0 2 2 3 6 14 R Chris Wagner 6 1 1 2 -2 6 6 R Brock Boeser 7 2 2 4 -4 8 17 C Ryan Donato 6 1 0 1 -3 2 8 D Christopher Tanev 7 0 3 3 -2 2 20 C Joakim Nordstrom 6 1 0 1 1 2 9 L Brendan Leipsic 3 1 0 1 -2 2 25 D Brandon Carlo 7 0 2 2 4 2 18 R Jake Virtanen 7 2 1 3 0 8 27 D John Moore 7 0 0 0 4 6 20 C Brandon Sutter 7 2 1 3 -1 2 33 D Zdeno Chara 7 1 1 2 -1 2 21 L Loui Eriksson 7 0 3 3 2 0 37 C Patrice Bergeron 7 6 7 13 5 4 23 D Alexander Edler 7 0 5 5 -1 10 42 R David Backes 7 0 0 0 0 4 26 L Antoine Roussel 3 1 0 1 -1 4 43 C Danton Heinen 5 0 1 1 1 6 27 D Ben Hutton 5 1 0 1 -4 10 44 D Steven Kampfer - - - - - - 44 D Erik Gudbranson 7 0 1 1 -1 21 46 C David Krejci 7 1 5 6 3 0 47 L Sven Baertschi 7 2 3 5 -2 2 48 D Matt Grzelcyk 7 0 3 3 1 2 51 D Troy Stecher 7 0 1 1 2 2 52 C Sean Kuraly 7 1 1 2 1 9 53 C Bo Horvat 7 4 1 5 -4 0 55 C Noel Acciari 7 0 0 0 -4 2 59 C Tim Schaller 5 0 2 2 -1 0 58 D Urho Vaakanainen - - - - - - 60 C Markus Granlund 7 1 2 3 4 0 63 L Brad Marchand -

2016 NHL DRAFT Buffalo, N.Y
2016 NHL DRAFT Buffalo, N.Y. • First Niagara Center Round 1: Fri., June 24 • 7 p.m. ET • NBC Sports Network Rounds 2-7: Sat., June 25 • 10 a.m. ET • NHL Network The Washington Capitals hold the 26th overall selection in the 2016 NHL Draft, which begins on Friday, June 24 at First Niagara Center in Buffalo, N.Y., and will be televised on NBC Sports Network at 7 p.m. Rounds 2-7 will take place on Saturday and will be televised on NHL Network at 10 a.m. The Capitals currently hold six picks in the seven-round draft. Last year, CAPITALS 2016 DRAFT PICKS the team made four selections, including goaltender Ilya Samsonov with the 22nd overall Round Selection(s) selection. 1 26 4 117 CAPITALS DRAFT NOTES 5 145 (from ANA via TOR) Homegrown – Fourteen players (Karl Alzner, Nicklas Backstrom, Andre Burakovsky, John 5 147 Carlson, Connor Carrick, Stanislav Galiev, Philipp Grubauer, Braden Holtby, Marcus 6 177 Johansson, Evgeny Kuznetsov, Dmitry Orlov, Alex Ovechkin, Chandler Stephenson and Tom 7 207 Wilson) who played for the Capitals in 2015-16 were originally drafted by Washington. Capitals draftees accounted for 60.9% of the team’s goals last season and 63.2% of the team’s FIRST-ROUND DRAFT ORDER assists. 1. Toronto Maple Leafs 2. Winnipeg Jets Pick 26 – This year marks the third time in franchise history the Capitals have held the 26nd 3. Columbus Blue Jackets overall selection in the NHL Draft. Washington selected Evgeny Kuznetsov with the 26th pick 4. Edmonton Oilers in the 2010 NHL Draft and Brian Sutherby with the 26th pick in the 2000 NHL Draft. -

A Great Season for Aurora's Rob Thomas
This page was exported from - The Auroran Export date: Thu Sep 30 17:47:02 2021 / +0000 GMT A great season for Aurora's Rob Thomas By Robert Belardi Before the season was halted due to COVID-19, Aurora native and centreman for the St. Louis Blues Robert Thomas was showing signs of improvement in his second season in the NHL. The Stanley Cup Champion recorded eight points in his last 10 games, including an 11-point month in February alone. His lone goal in that spell came against the Chicago Blackhawks at home, back on February 25 to bring the Blues within one goal in the second period. A cross-ice pass from David Perron found Thomas alone in front of goal and the 20-year-old roofed the puck short side. In total this year, Thomas has recorded 10 goals and 32 assists, along with a plus-minus rating of nine. He recorded nine goals and 24 assists in his rookie season last year. He's a quick skater, an agile forward with a nose for the puck and vision like a hawk down the ice. According to SB Nation writer Dan Buffa, written on March 6, Thomas belongs in St. Louis for a long time. In fact, Thomas was almost traded from St. Louis in exchange for Ryan O'Reilly to Buffalo on July 1, 2018. How different the roster would have been if he left. Thankfully, the Blues valued him more than that. The 20th overall draft pick in 2017 adds depth in the centre position that has O'Reilly and Brayden Schenn in the second and first line above him. -

2007 SC Playoff Summaries
PITTSBURGH PENGUINS STANLEY CUP CHAMPIONS 2 0 0 9 Craig Adams, Philippe Boucher, Matt Cooke, Sidney Crosby CAPTAIN, Pascal Dupuis, Mark Eaton, Ruslan Fedotenko, Marc-Andre Fleury, Mathieu Garon, Hal Gill, Eric Godard, Alex Goligoski, Sergei Gonchar, Bill Guerin, Tyler Kennedy, Chris Kunitz, Kris Letang, Evgeni Malkin, Brooks Orpik, Miroslav Satan, Rob Scuderi, Jordan Staal, Petr Sykora, Maxime Talbot, Mike Zigomanis Mario Lemieux CO-OWNER/CHAIRMAN Ray Shero GENERAL MANAGER, Dan Bylsma HEAD COACH © Steve Lansky 2010 bigmouthsports.com NHL and the word mark and image of the Stanley Cup are registered trademarks and the NHL Shield and NHL Conference logos are trademarks of the National Hockey League. All NHL logos and marks and NHL team logos and marks as well as all other proprietary materials depicted herein are the property of the NHL and the respective NHL teams and may not be reproduced without the prior written consent of NHL Enterprises, L.P. Copyright © 2010 National Hockey League. All Rights Reserved. 2009 EASTERN CONFERENCE QUARTER—FINAL 1 BOSTON BRUINS 116 v. 8 MONTRÉAL CANADIENS 93 GM PETER CHIARELLI, HC CLAUDE JULIEN v. GM/HC BOB GAINEY BRUINS SWEEP SERIES Thursday, April 16 1900 h et on CBC Saturday, April 18 2000 h et on CBC MONTREAL 2 @ BOSTON 4 MONTREAL 1 @ BOSTON 5 FIRST PERIOD FIRST PERIOD 1. BOSTON, Phil Kessel 1 (David Krejci, Chuck Kobasew) 13:11 1. BOSTON, Marc Savard 1 (Steve Montador, Phil Kessel) 9:59 PPG 2. BOSTON, David Krejci 1 (Michael Ryder, Milan Lucic) 14:41 2. BOSTON, Chuck Kobasew 1 (Mark Recchi, Patrice Bergeron) 15:12 3. -

Turnbull Hockey Pool For
Turnbull Hockey Pool for Each year, Turnbull students participate in several fundraising initiatives, which we promote as a way to develop a sense of community, leadership and social responsibility within the students. Last year's grade 7 and 8 students put forth a great deal of effort campaigning friends and family members to join Turnbull's annual NHL hockey pool, raising a total of $1750 for a charity of their choice (the United Way). This year's group has decided to run the hockey pool for the benefit of Help Lesotho, an international development organization working in the AIDS-ravaged country of Lesotho in southern Africa. From www.helplesotho.org "Help Lesotho’s programs foster hope and motivation in those who are most in need: orphans, vulnerable children, at-risk youth and grandmothers. Our work targets root causes and community priorities, including literacy, youth leadership training, school twinning, child sponsorship and gender programming. Help Lesotho is an effective, sustainable organization that is working at the grass-roots level to support the next generation of leaders in Lesotho." Your participation in this year's NHL hockey pool is very much appreciated. We believe it will provide students and their friends and families an opportunity to have fun together while giving back to their community by raising awareness and funds for a great cause. Prizes: > Grand Prize awarded to contestant whose team accumulates the most points over the regular NHL season = 10" Samsung Galaxy Tablet > Monthly Prizes awarded to the contestants whose teams accumulate the most points over each designated period (see website) = Two Movie Passes How it Works: > Everyone in the community is welcome to join in on the fun. -

NUORET KONKARIT Teksti: Terry Zulynik Kuvat: Dave Sandford/Iihf/Hhof
NUORET KONKARIT teksti: terry zulynik kuvat: dave sandford/iihf/hhof Daniel ja Henrik Sedin ovat nyt, 23-vuotiaina, jo neljän nhl-kauden parkkiinnuttamia kiekkoammattilaisia. Tällä kaudella he tekivät uudet piste-ennätyksensä. Ehkä heitä ei vielä kannatakaan unohtaa? 22.3.2004 – Takana oli tappiot Colum- konferenssin voitosta, jäi pariksi viikoksi bukselle ja Chicagolle, nhl:n huonoim- mediamyrskyyn ja kaukalon ulkopuo- mille joukkueille vielä. Kaikki tiesivät, liset tapahtumat murensivat joukkueen että edessä olisi rankat harjoitukset – ja he pelaajien keskittymisen. Vielä kaksi olivat oikeassa. viikkoa aikaisemmin Canucks oli ollut Kaukalossa oli liian hiljaista, huulen- enemmän kuin vahva ehdokas jopa Stanley heitto ja kujeilu loistivat poissaolollaan. Cup –voittajaksi. Nyt jäällä on murtunut Jäällä oli selvästi Todd Bertuzzin päälle- joukkue, joka nuolee haavojaan, paran- karkauksen jälkiseuraustena mykistämä telee loukkaantumisiaan ja yrittää kaikin ja tainnuttama joukkue. Bertuzzi tyrmäsi keinoin pitää itseluottamusta nakertavat Colorado Avalanchen muutama viikko epäilyt loitolla. aikaisemmin, tunnetuin seurauksin. Siellä jossakin, keskellä kaikkea kohua, Moorelta murtui niskanikama, kun hän kaikkea hälinää, kaikkea järkytystä, ovat kaatui Bertuzzin takaapäin tulleen lyönnin Daniel ja Henrik Sedin, joiden tasaisen voimasta jäähän ja sai kaiken huipuksi varma peli oli Canucksin valopilkkuja päälleen reilun satakiloisen Bertuzzin ja kaudella 2003–04. pari muuta pelaajaa. Bertuzzi sai pelikiel- Vancouver Canucksin toimitusjohta- lon kauden loppuun saakka. ja Brian Burke vaihtoi Bryan McCaben Vancouver Canucks, joka vielä pari ja seuraavan vuoden ykköskierroksen viikkoa aikaisemmin taisteli Läntisen varausvuoron saadakseen Daniel ja Henrik 84 Sedinin samaan nhl-joukkueeseen. Burke Uutuuden viehätys ja adrenaliini siivitti- oli valmis maksamaan Sedineistä aika vätkin heitä ensimmäiset 20 ottelua. Sitten kalliin hinnan – ja mies tunnetaan kovana sarjan rankkuus (Canucks pelasi yhdessä tinkijänä. -

3Rd Call 5Th International Conference on Soil-, Bio- and Eco-Engineering
3rd Call 5th International Conference on Soil-, Bio- and Eco-Engineering in 2021: Bern, Switzerland 21. – 25. June 2021 Institution: Bern University of Applied Sciences, EcorisQ, Address: Laenggasse 85, 3052 Zollikofen, Bern, Switzerland https://www.hafl.bfh.ch/ueber-die-hafl/campus/bildergalerie.html Conference themes include: • Root-soil interactions and distribution • Root reinforcement • Soil erosion and conservation • Riverbank and coastline protection measures • Slope stability modelling • Effects of vegetation on hillslope hydrology • Bioengineering, ecology, and biodiversity • Eco-DRR measures, protection forests, and soil Bioengineering • Risk management and decision support systems • Benefits and liabilities in slope and erosion control Local organizing committee and affiliations: Prof. Jean-Jacques Thormann Bern University of Applied Sciences, School of Agricultural, Forest and Food Sciences HAFL, Bern, Switzerland Prof. Dr. Luuk Dorren Bern University of Applied Sciences, School of Agricultural, Forest and Food Sciences HAFL, Bern, Switzerland; EcorisQ Dr. Massimiliano Schwarz Bern University of Applied Sciences, School of Agricultural, Forest and Food Sciences HAFL, Bern, Switzerland; EcorisQ Dominik May Bern University of Applied Sciences, School of Agricultural, Forest and Food Sciences HAFL, Bern, Switzerland Niels Hollard Bern University of Applied Sciences, School of Agricultural, Forest and Food Sciences HAFL, Bern, Switzerland Dr. Filippo Giadrossich Department of Agriculture, University of Sassari, Sassari, Italy Dr. Denis Cohen Department of Earth and Environmental Science, New Mexico Tech, Socorro, NM, USA Prof. Dr. Gian Battista Bischetti Department of Agricultural and Environmental Science, University of Milan, Milan, Italy Dr. Alexia Stokes French National Institute for Agricultural Research INRA, University of Montpellier, Montpellier, France Additionally, local partners will be involved (i.e., Cantons, private companies, Swiss Federal Office for the Environment).