DOCSLIB.ORG

Analytic Approaches to the Study of Small Scale Structure on Cosmic String Networks

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Analytic Approaches to the Study of Small Scale Structure on Cosmic String Networks UNIVERSITY of CALIFORNIA Santa Barbara Analytic Approaches to the Study of Small Scale Structure on Cosmic String Networks A dissertation submitted in partial satisfaction of the requirements for the degree of Doctor of Philosophy in Physics by Jorge V. Rocha arXiv:0812.4020v1 [gr-qc] 20 Dec 2008 Committee in charge: Professor Joseph Polchinski, Chair Professor Tommaso Treu Professor Donald Marolf September 2008 The dissertation of Jorge V. Rocha is approved: Professor Tommaso Treu Professor Donald Marolf Professor Joseph Polchinski, Chair August 2008 Analytic Approaches to the Study of Small Scale Structure on Cosmic String Networks Copyright 2008 by Jorge V. Rocha iii To my parents, Carlos and Isabel iv Acknowledgements In writing these lines I think of the people without whom I would not be writing these lines. To the person who taught me the inner workings of science, Joe Polchinski, I am deeply grateful. Thank you, Joe, for sharing your knowledge and insight with me, for showing me the way whenever I got off track and for your powerful educated guesses. Over these years I have also had the opportunity of collaborating with Florian Dubath. For this and for his enthusiasm I am thankful. I was fortunate enough to have Don Marolf and Tommaso Treu as committee members. I learned much about physics from Don, and always with a good feeling about it. I am grateful for your constructive criticism as well. From Tommaso I appreciate him always keeping an open door for me and also showing so much interest. I thank both of you for all that. Having spent these years in UCSB I have benefited from the excellence of the local Physics Department, either through classes, gravity lunches or simple conversations. I wish to thank Professors Ski Antonucci, David Berenstein, Matt Fisher, Steve Giddings, Sergei Gukov, Jim Hartle, Gary Horowitz, Peng Oh, Mark Srednicki, Bob Sugar and Tony Zee. Now going back further in time, I am grateful to Professors Jo˜ao Pimentel Nunes and Jos´eMour˜ao, who advised me during the last years of undergraduate studies in Lisbon. Thank you for introducing me to the wonders of string theory and for all your support that led me here. I have also benefited from the presence of many former and fellow students of the high energy theory and gravity groups at UCSB, as well as postdocs. I would like to thank those who taught me one way or another, either through journal club talks and discussions, interactions in classes (as classmates or TAs), or simply by sharing the office with me. These people include Aaron Amsel, Curtis Asplund, Dan Balick, Charlie Beil, Johannes Br¨odel, Geoffrey Comp`ere, Keith Copsey, Richard Eager, Henriette Elvang, Ted Erler, Scott Fraser, Mike Gary, Misato Hayashida, Sungwoo Hong, Matt Lippert, Anshuman Maharana, Nelia Mann, Ian Morrison, Jacopo Orgera, Jo˜ao Penedones, Matt Pillsbury, Sam Pinansky, Matt Roberts, Sam Vazquez, Amitabh Virmani and Sho Yaida. My friends in Santa Barbara also helped making these years more enjoyable. Among the ones I haven’t already mentioned are Biliana, Carlos, Cec´ılia, Coral, Daniel, Eduardo, German, Gokhan, James, Jo˜ao, Jonathan, Larisa, Lu, Melissa, Pedro, Ricardo, Rishi, Sabine, Scott, Sofia and Susana. Furthermore, I would like to thank our neighbors at Family Student Housing who contributed to make it such a nice place to live at, and my soccer buddies for times well spent on the v field. On the financial side, I acknowledge support from Funda¸c˜ao para a Ciˆencia e a Tecnologia through grant SFRH/BD/12241/2003, which allowed me to focus more on research, rather than worrying about more mundane issues. I saved for last the people I love and care for most deeply. I would not have reached this point in my life if it had not been for the ones who brought me up and educated me. Thank you Mother, thank you Father, for your constant support and encouragement. I am also very happy (and proud, I admit) to say thank you to my daughter Sara, who keeps on showing me how joyful life can be, specially when she displays the most beautiful smile I have ever seen. Finally, to you, Susana, I am more grateful than I can express. Thanks for sharing my life over all these years, and for sharing your life with me. Thank you for putting up with me through all the bad moments (helping me keep my mental sanity!) and for inflating the good ones. Thank you for your contagious happiness. And thank you for giving me Sara. vi Curriculum Vitæ Jorge V. Rocha Education 2008 PhD in Physics, University of California, Santa Barbara 2002 Licenciado in Technological Physics Engineering, Instituto Superior T´ecnico, Lisbon, Portugal Publications “Analytic study of small scale structure on cosmic strings”, J. Polchinski and J. V. Rocha, published in Phys.Rev.D74:083504,2006, e-print: hep-ph/0606205. “Cosmic string structure at the gravitational radiation scale”, J. Polchinski and J. V. Rocha, published in Phys.Rev.D75:123503,2007, e-print: gr-qc/0702055. “Periodic gravitational waves from small cosmic string loops”, F. Dubath and J. V. Rocha, published in Phys.Rev.D76:024001,2007, e-print: gr-qc/0703109. “Scaling solution for small cosmic string loops”, J. V. Rocha, published in Phys. Rev.Lett.100:071601,2008, e-print: arXiv:0709.3284 [gr-qc]. “Cosmic String Loops, Large and Small”, F. Dubath, J. Polchinski and J. V. Rocha, published in Phys.Rev.D77:123528,2008, e-print: arXiv:0711.0994 [astro-ph]. “Evaporation of large black holes in AdS: coupling to the evaporon”, J. V. Rocha, e-print: arXiv:0804.0055 [hep-th]. Honors and Awards 2003 Broida fellowship award 2003 Doctoral fellowship from Funda¸c˜ao para a Ciˆencia e a Tec- nologia (Portugal) vii Abstract Analytic Approaches to the Study of Small Scale Structure on Cosmic String Networks by Jorge V. Rocha We present an analytic model specifically designed to address the long standing issue of small scale structure on cosmic string networks. The model is derived from the microscopic string equations, together with a few motivated assumptions. The resulting form of the correlation between two points on a string is exploited to study smoothing by gravitational radiation, loop formation and lensing by cosmic strings. In addition, the properties of the small loop population and the possibility of detecting gravitational waves generated by their lowest harmonics are investigated. Whenever possible, we compare the predictions of the model to the most recent numerical simulations of cosmic string networks. viii Contents Contents ix List of Figures xi List of Tables xiii 1 Introduction 1 1.1 Cosmicstrings:whatarethey? . 1 1.2 Cosmic strings in our universe? . 3 1.3 Cosmicsuperstrings.......................... 5 1.4 Networksofcosmicstrings ...................... 6 1.4.1 The scaling regime . 8 1.4.2 Smallscalestructure ..................... 9 1.4.3 Analyticapproaches ..................... 10 1.5 Outline................................. 11 2 Model for small scale structure 13 2.1 Preliminaries: Basic ingredients . 14 2.2 Assumptionsofthemodel . .. .. 19 2.3 Two-pointfunctionsatshortdistance . 20 2.3.1 Small fluctuation approximation . 24 2.4 Discussion............................... 25 3 Gravitational radiation from cosmic strings 30 3.1 Radiation from long strings and back-reaction . 31 3.2 Radiationandback-reactionimproved . 35 3.3 The long-string two-point function revisited . 38 3.4 Smallscalestructureandcusps . 41 ix 4 Loop formation 43 4.1 General results: loops, cusps and kinks . 43 4.2 Therateofloopproduction . .. .. 45 4.2.1 Preliminary considerations . 45 4.2.2 Calculation of the rate . 47 4.2.3 The normalization . 51 4.3 Discussion............................... 53 4.3.1 Comparison with simulations . 54 4.3.2 Effect of loop production on the two-point function . 56 4.3.3 Fragmentation......................... 57 4.3.4 Largeloops .......................... 58 5 Properties of the small loop population 60 5.1 Phenomenologyofsmallloops . 60 5.1.1 Gravitational radiation from small loops and their lifetimes 60 5.1.2 Loop velocities and cusps . 62 5.1.3 Amodelloop ......................... 63 5.2 Scalingoftheloopnumberdensity . 66 5.2.1 Preliminaries . 66 5.2.2 Evolution neglecting gravitational radiation . 67 5.2.3 Evolution including gravitational radiation . 68 6 Some implications for observation 71 6.1 Lensing ................................ 71 6.1.1 Distortion of images . 72 6.1.2 Alignment of lenses and non-Gaussianity . 75 6.2 Periodic gravitational waves from small cosmic string loops . 77 6.2.1 EmissionofGW ....................... 78 6.2.2 Visibility of the small loops . 81 6.2.3 Loop number density and expected number of detections . 85 6.2.4 Summaryanddiscussion . 88 7 Final Remarks 90 A Gaussian averages 92 B The matter-radiation transition 96 Bibliography 98 x List of Figures 1.1 The usual quartic “Mexican hat” potential for the complex Higgs field φ(x) is shown on the left. A vortex string configuration maps spacetime points belonging to the core of the string (on the right side of the figure) to the local maximum of the potential V (φ) and large circles surrounding the string to the ring of degenerate minima of V ................................... 2 2.1 The top panel shows an intercommutation event in which two seg- ments of string exchange partners. The bottom panel displays a single cosmic string self-intersecting and chopping off a loop. In such processes pairs of kinks are formed on the intervening seg- ments and travel in opposite directions along the string. 18 2.2 Comparison of the model (dashed line) with the data provided by C. Martins and E. P. S. Shellard (solid red line) in the radiation- dominated era, for which the correlation length is ξ 0.30t. ... 27 2.3 Comparison of the model (dashed line) with the data≃ provided by C.
Load more

Recommended publications
  • String Theory. Volume 1, Introduction to the Bosonic String
    This page intentionally left blank String Theory, An Introduction to the Bosonic String The two volumes that comprise String Theory provide an up-to-date, comprehensive, and pedagogic introduction to string theory. Volume I, An Introduction to the Bosonic String, provides a thorough introduction to the bosonic string, based on the Polyakov path integral and conformal field theory. The first four chapters introduce the central ideas of string theory, the tools of conformal field theory and of the Polyakov path integral, and the covariant quantization of the string. The next three chapters treat string interactions: the general formalism, and detailed treatments of the tree-level and one loop amplitudes. Chapter eight covers toroidal compactification and many important aspects of string physics, such as T-duality and D-branes. Chapter nine treats higher-order amplitudes, including an analysis of the finiteness and unitarity, and various nonperturbative ideas. An appendix giving a short course on path integral methods is also included. Volume II, Superstring Theory and Beyond, begins with an introduction to supersym- metric string theories and goes on to a broad presentation of the important advances of recent years. The first three chapters introduce the type I, type II, and heterotic superstring theories and their interactions. The next two chapters present important recent discoveries about strongly coupled strings, beginning with a detailed treatment of D-branes and their dynamics, and covering string duality, M-theory, and black hole entropy. A following chapter collects many classic results in conformal field theory. The final four chapters are concerned with four-dimensional string theories, and have two goals: to show how some of the simplest string models connect with previous ideas for unifying the Standard Model; and to collect many important and beautiful general results on world-sheet and spacetime symmetries.
    [Show full text]
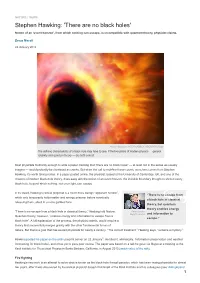
  • Stephen Hawking: 'There Are No Black Holes' Notion of an 'Event Horizon', from Which Nothing Can Escape, Is Incompatible with Quantum Theory, Physicist Claims
    NATURE | NEWS Stephen Hawking: 'There are no black holes' Notion of an 'event horizon', from which nothing can escape, is incompatible with quantum theory, physicist claims. Zeeya Merali 24 January 2014 Artist's impression VICTOR HABBICK VISIONS/SPL/Getty The defining characteristic of a black hole may have to give, if the two pillars of modern physics — general relativity and quantum theory — are both correct. Most physicists foolhardy enough to write a paper claiming that “there are no black holes” — at least not in the sense we usually imagine — would probably be dismissed as cranks. But when the call to redefine these cosmic crunchers comes from Stephen Hawking, it’s worth taking notice. In a paper posted online, the physicist, based at the University of Cambridge, UK, and one of the creators of modern black-hole theory, does away with the notion of an event horizon, the invisible boundary thought to shroud every black hole, beyond which nothing, not even light, can escape. In its stead, Hawking’s radical proposal is a much more benign “apparent horizon”, “There is no escape from which only temporarily holds matter and energy prisoner before eventually a black hole in classical releasing them, albeit in a more garbled form. theory, but quantum theory enables energy “There is no escape from a black hole in classical theory,” Hawking told Nature. Peter van den Berg/Photoshot and information to Quantum theory, however, “enables energy and information to escape from a escape.” black hole”. A full explanation of the process, the physicist admits, would require a theory that successfully merges gravity with the other fundamental forces of nature.
    [Show full text]
  • Anomalies, Dualities, and Topology of D = 6 N = 1 Superstring Vacua
    RU-96-16 NSF-ITP-96-21 CALT-68-2057 IASSNS-HEP-96/53 hep-th/9605184 Anomalies, Dualities, and Topology of D =6 N =1 Superstring Vacua Micha Berkooz,1 Robert G. Leigh,1 Joseph Polchinski,2 John H. Schwarz,3 Nathan Seiberg,1 and Edward Witten4 1Department of Physics, Rutgers University, Piscataway, NJ 08855-0849 2Institute for Theoretical Physics, University of California, Santa Barbara, CA 93106-4030 3California Institute of Technology, Pasadena, CA 91125 4Institute for Advanced Study, Princeton, NJ 08540 Abstract We consider various aspects of compactifications of the Type I/heterotic Spin(32)/Z2 theory on K3. One family of such compactifications in- cludes the standard embedding of the spin connection in the gauge group, and is on the same moduli space as the compactification of arXiv:hep-th/9605184v1 25 May 1996 the heterotic E8 × E8 theory on K3 with instanton numbers (8,16). Another class, which includes an orbifold of the Type I theory re- cently constructed by Gimon and Polchinski and whose field theory limit involves some topological novelties, is on the moduli space of the heterotic E8 × E8 theory on K3 with instanton numbers (12,12). These connections between Spin(32)/Z2 and E8 × E8 models can be demonstrated by T duality, and permit a better understanding of non- perturbative gauge fields in the (12,12) model. In the transformation between Spin(32)/Z2 and E8 × E8 models, the strong/weak coupling duality of the (12,12) E8 × E8 model is mapped to T duality in the Type I theory. The gauge and gravitational anomalies in the Type I theory are canceled by an extension of the Green-Schwarz mechanism.
    [Show full text]
  • Eternal Inflation and Its Implications
    IOP PUBLISHING JOURNAL OF PHYSICS A: MATHEMATICAL AND THEORETICAL J. Phys. A: Math. Theor. 40 (2007) 6811–6826 doi:10.1088/1751-8113/40/25/S25 Eternal inflation and its implications Alan H Guth Center for Theoretical Physics, Laboratory for Nuclear Science, and Department of Physics, Massachusetts Institute of Technology, Cambridge, MA 02139, USA E-mail: [email protected] Received 8 February 2006 Published 6 June 2007 Online at stacks.iop.org/JPhysA/40/6811 Abstract Isummarizetheargumentsthatstronglysuggestthatouruniverseisthe product of inflation. The mechanisms that lead to eternal inflation in both new and chaotic models are described. Although the infinity of pocket universes produced by eternal inflation are unobservable, it is argued that eternal inflation has real consequences in terms of the way that predictions are extracted from theoretical models. The ambiguities in defining probabilities in eternally inflating spacetimes are reviewed, with emphasis on the youngness paradox that results from a synchronous gauge regularization technique. Although inflation is generically eternal into the future, it is not eternal into the past: it can be proven under reasonable assumptions that the inflating region must be incomplete in past directions, so some physics other than inflation is needed to describe the past boundary of the inflating region. PACS numbers: 98.80.cQ, 98.80.Bp, 98.80.Es 1. Introduction: the successes of inflation Since the proposal of the inflationary model some 25 years ago [1–4], inflation has been remarkably successful in explaining many important qualitative and quantitative properties of the universe. In this paper, I will summarize the key successes, and then discuss a number of issues associated with the eternal nature of inflation.
    [Show full text]
  • 2000 Annual Report
    2001 ANNUAL REPORT ALFRED P. SLOAN FOUNDATION 1 CONTENTS 2001 Grants and Activities Science and Technology 5 Fellowships 5 Sloan Research Fellowships 5 Direct Support of Research 9 Neuroscience 9 Computational Molecular Biology 9 Limits to Knowledge 10 Marine Science 11 Other Science and Science Policy 15 History of Science and Technology 16 Standard of Living and Economic Performance 17 Industries 17 Industry Centers 17 Human Resources/Jobs/Income 21 Globalization 21 Business Organizations 22 Economics Research and Other Work 24 Nonprofit Sectors 26 Universities 26 Assessment of Government Performance 26 Work, Workforce and Working Families 30 Centers on Working Families 30 Workplace Structure and Opportunity 31 Working Families and Everyday Life 34 Education and Careers in Science and Technology 36 Scientific and Technical Careers 36 Anytime, Anyplace Learning 36 Professional Master’s Degrees 42 Information about Careers 47 Entry and Retention 48 Science and Engineering Education 48 Education for Minorities and Women 49 Minorities 49 Women 53 Public Understanding of Science and Technology 55 Books 55 Sloan Technology Book Series 57 Radio 58 2 Public Television 59 Commercial Television and Films 60 Theater 61 General 63 Selected National Issues and The Civic Program 64 Selected National Issues 64 September 11 64 Bioterrorism 66 Energy 68 Federal Statistics 69 Public Policy Research 69 The Civic Program 71 Additional Grants 73 2001 Financial Report Financial Review 75 Auditors’ Report 76 Balance Sheets 77 Statements of Activities 78 Statements of Cash Flows 79 Notes to Financial Statements 80 Schedules of Management and Investment Expenses 83 3 2001 GRANTS AND ACTIVITIES 4 SCIENCE AND TECHNOLOGY FELLOWSHIPS Sloan Research Fellowships $4,160,000 The Sloan Research Fellowship Program aims to stimulate fundamental research by young scholars with outstanding promise to contribute significantly to the advancement of knowledge.
    [Show full text]
  • Spring 2007 Prizes & Awards
    APS Announces Spring 2007 Prize and Award Recipients Thirty-nine prizes and awards will be presented theoretical research on correlated many-electron states spectroscopy with synchrotron radiation to reveal 1992. Since 1992 he has been a Permanent Member during special sessions at three spring meetings of in low dimensional systems.” the often surprising electronic states at semicon- at the Kavli Institute for Theoretical Physics and the Society: the 2007 March Meeting, March 5-9, Eisenstein received ductor surfaces and interfaces. His current interests Professor at the University of California at Santa in Denver, CO, the 2007 April Meeting, April 14- his PhD in physics are self-assembled nanostructures at surfaces, such Barbara. Polchinski’s interests span quantum field 17, in Jacksonville, FL, and the 2007 Atomic, Mo- from the University of as magnetic quantum wells, atomic chains for the theory and string theory. In string theory, he dis- lecular and Optical Physics Meeting, June 5-9, in California, Berkeley, in study of low-dimensional electrons, an atomic scale covered the existence of a certain form of extended Calgary, Alberta, Canada. 1980. After a brief stint memory for testing the limits of data storage, and structure, the D-brane, which has been important Citations and biographical information for each as an assistant professor the attachment of bio-molecules to surfaces. His in the nonperturbative formulation of the theory. recipient follow. The Apker Award recipients ap- of physics at Williams more than 400 publications place him among the His current interests include the phenomenology peared in the December 2006 issue of APS News College, he moved to 100 most-cited physicists.
    [Show full text]
  • PDF Document
    String theorists win Dirac Medal P-2 Is string theory a theory or a framework? What impacts will the Large Hadron Collider experiments have on the field? ICTP Dirac Medallists Juan Martín Maldacena, Joseph Polchinski and Cumrun Vafa share their insights on this proposal for a unified description of fundamental interactions in nature, and also describe what they find most exciting about string theory • • • ICTP celebrates Year of Darwin P-5 The link between physics and human evolution may not seem immediately obvious. Yet, the tools of modern physics can date human evolution and dispersal accurately. The tools and techniques used to pinpoint the age of human bones and teeth were the subject of an ICTP exhibit and lecture series held in conjunction with UNESCO’s symposium on Darwin, Evolution and Science • • • Focus on Africa CENTREFOLD ICTP has a long tradition of scientific capacity-building in Africa. Registrazione presso il Tribunale di Trieste n. 1044 del 01.03.2002 | Contiene Inserto Redazionale n. 1044 del 01.03.2002 | Contiene Inserto di Trieste il Tribunale presso Registrazione Over the last few decades, ICTP has supported numerous activities throughout the continent, including training programmes, networks and the establishment of affiliate centres. In Trieste, ICTP has welcomed more than 10,000 African visitors since 1970, providing advanced research and NEWSNEWS training opportunities unavailable to scientists in their home countries • • • NEW SCIENCE FOR CLEAN ENERGY (P-6) | EXPERIMENTAL PLASMA PHYSICS n°127 AT ICTP (P-7) | SNO DIRECTOR VISITS ICTP (P-8) | RESEARCH NEWS BRIEFS Spring/Summer 2009 (P-12) | NEW STAFF (P-16) | ACHIEVEMENTS/PRIZES (P-17) from ICTP Poste Italiane S.p.A.
    [Show full text]
  • Black Holes and Entanglement Entropy
    Black holes and entanglement entropy Thesis by Pouria Dadras In Partial Fulfillment of the Requirements for the Degree of Doctor of Philosophy in Physics CALIFORNIA INSTITUTE OF TECHNOLOGY Pasadena, California 2021 Defended May 18, 2021 ii © 2021 Pouria Dadras ORCID: 0000-0002-5077-3533 All rights reserved iii ACKNOWLEDGEMENTS First and foremost, I am truly indebted to my advisor, Alexei Kitaev, for many reasons: providing an atmosphere in which my only concern was doing research, teaching me how to deal with a hard problem, how to breaking it into small parts and solving each, many helpful suggestions and discussions tht we had in the past five years that I was his students, sharing some of his ideas and notes with me, ··· . I am also grateful to the other members of the Committee, Sean Carroll, Anton Kapustin, and David Simmons-Duffin for joining my talk, and also John Preskill for joining my Candidacy exam and having discussions. I am also grateful to my parents in Iran who generously supported me during the time that I have been in the United states. I am also Thankful to my friends, Saeed, Peyman, Omid, Fariborz, Ehsan, Aryan, Pooya, Parham, Sharareh, Pegah, Christina, Pengfei, Yingfei, Josephine, and others. iv ABSTRACT We study the deformation of the thermofield-double ¹TFDº under evolution by a double-traced operator by computing its entanglement entropy. After saturation, the entanglement change leads to the temperature change. In Jackiw-Teitelboim gravity, the new temperature can be computed independently from two- point function by considering the Schwarzian modes. We will also derive the entanglement entropy from the Casimir associated with the SL(2,R) symmetry.
    [Show full text]
  • 1 Literature
    Liverpool Lectures on String Theory Guide to the Literature Thomas Mohaupt Semester 1, 2008/2009 1 Literature • Katrin Becker, Melanie Becker and John H. Schwarz, String Theory and M Theory, A modern introduction (2007). The most recent textbook, attempts to give an introduction from a con- temporary perspective and to treats virtually all recent developments. More advanced than Zwiebach, but according to many colleagues very ac- cessible and not too technical. If you want to have just one book which 'covers it all', this is currently the best choice. • Barton Zwiebach, A First Course in String Theory (2004). The most accessible textbook. Does not cover advanced or technical as- pects, but includes recent developments such as brane world model build- ing and black hole entropy. • Joseph Polchinski, String Theory (2 Volumes, 1998). For many the standard textbook. Includes developments of the mid- nineties, such as D-branes. Covers many technical aspects, but is (by opinion of many readers) not detailed enough to learn 'how it's done' without accompanying lectures or further literature. • Michael B. Green, John H. Schwarz and Edward Witten, Superstring The- ory (2 volumes, 1987). The classical textbook. Though it does not cover the 'modern stuff', it is a good reference if you need to know the details of the 'old stuff'. • Dieter L¨ustand Stefan Theisen, Lectures on String Theory (1989). Concise, technical exposition of the 'old stuff'. Covers material that is not in Green, Schwarz, Witten. Out of print (I have a copy), and no easy/first read. • Thomas Mohaupt, Introduction to String Theory (hep-th/0207249).
    [Show full text]
  • 2017 Breakthrough Prizes in Mathematics and Fundamental
    COMMUNICATION 2017 Breakthrough Prizes Awarded Jean Bourgain Joseph Polchinski Andrew Strominger Cumrun Vafa Breakthrough Prize in Mathematics be obtained from the results of Weil and Deligne on the Jean Bourgain of the Institute for Advanced Study, Riemann hypothesis over finite fields), as well as the de- Princeton, New Jersey, has been selected as the recipient velopment (with Gamburd and Sarnak) of the affine sieve of the 2017 Breakthrough Prize in Mathematics by the that has proven to be a powerful tool for analyzing thin Breakthrough Prize Foundation. Bourgain was honored for groups. Most recently, with Demeter and Guth, Bourgain “major contributions across an incredibly diverse range of has established several important decoupling theorems areas, including harmonic analysis, functional analysis, er- in Fourier analysis that have had applications to partial godic theory, partial differential equations, mathematical differential equations, combinatorial incidence geometry, physics, combinatorics, and theoretical computer science.” and analytic number theory, in particular solving the Main The prize carries a cash award of US$3 million. Conjecture of Vinogradov, as well as obtaining new bounds The Notices asked Terence Tao of the University of Cal- on the Riemann zeta function.” ifornia Los Angeles to comment on the work of Bourgain (Tao was on the Breakthrough Prize committee and was Biographical Sketch: Jean Bourgain also one of the nominators of Bourgain). Tao responded: Jean Bourgain was born in 1954 in Oostende, Belgium. He “Jean Bourgain is an unparalleled problem-solver in anal- received his PhD (1977) and his habilitation (1979) from ysis who has revolutionized many areas of the subject by the Free University of Brussels.
    [Show full text]
  • Full White Paper
    LIGO SCIENTIFIC COLLABORATION VIRGO COLLABORATION Document Type LIGO–T1400054 VIR-0176A-14 The LSC-Virgo White Paper on Gravitational Wave Searches and Astrophysics (2014-2015 edition) The LSC-Virgo Search Groups, the Data Analysis Software Working Group, the Detector Characterization Working Group and the Computing Committee WWW: http://www.ligo.org/ and http://www.virgo.infn.it Processed with LATEX on 2014/11/21 The LSC-Virgo White Paper on Gravitational Wave Searches and Astrophysics Contents 1 The LSC-Virgo White Paper on Data Analysis 4 1.1 Searches for Signals from Compact Binary Coalescences . .5 1.2 Searches for Generic Transients, or Bursts . .7 1.3 Searches for Continuous Wave Signals . .9 1.4 Searches for Stochastic Gravitational Wave Backgrounds . 11 1.5 Characterization of the Detectors and their Data . 13 1.6 Data Calibration . 15 1.7 Hardware Injections . 16 1.8 Computing and Software . 17 2 Previous Accomplishments (2013-2014) 19 2.1 Burst Working Group . 19 2.2 Compact Binary Coalescences Working Group . 19 2.3 Continuous Waves Group . 20 2.4 Stochastic Group . 21 2.5 Detector Characterization . 21 3 Search Plans for the Advanced Detector Era 23 3.1 All-Sky Burst Search . 24 3.2 Search For Binary Neutron Star Coalescences . 29 3.3 Search for Stellar-Mass Binary Black Hole Coalescences . 37 3.4 Search For Neutron Star – Black Hole Coalescences . 45 3.5 Search for GRB Sources of Transient Gravitational Waves . 57 3.6 Search for Intermediate Mass Black Hole Binary Coalescences . 64 3.7 All-sky Searches for Isolated Spinning Neutron Stars .
    [Show full text]
  • Memories of a Theoretical Physicist
    Memories of a Theoretical Physicist Joseph Polchinski Kavli Institute for Theoretical Physics University of California Santa Barbara, CA 93106-4030 USA Foreword: While I was dealing with a brain injury and finding it difficult to work, two friends (Derek Westen, a friend of the KITP, and Steve Shenker, with whom I was recently collaborating), suggested that a new direction might be good. Steve in particular regarded me as a good writer and suggested that I try that. I quickly took to Steve's suggestion. Having only two bodies of knowledge, myself and physics, I decided to write an autobiography about my development as a theoretical physicist. This is not written for any particular audience, but just to give myself a goal. It will probably have too much physics for a nontechnical reader, and too little for a physicist, but perhaps there with be different things for each. Parts may be tedious. But it is somewhat unique, I think, a blow-by-blow history of where I started and where I got to. Probably the target audience is theoretical physicists, especially young ones, who may enjoy comparing my struggles with their own.1 Some dis- claimers: This is based on my own memories, jogged by the arXiv and IN- SPIRE. There will surely be errors and omissions. And note the title: this is about my memories, which will be different for other people. Also, it would not be possible for me to mention all the authors whose work might intersect mine, so this should not be treated as a reference work.
    [Show full text]