Smoothed Particle Hydrodynamics (SPH): an Overview and Recent Developments
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Meshfree Methods Chapter 1 — Part 1: Introduction and a Historical Overview
MATH 590: Meshfree Methods Chapter 1 — Part 1: Introduction and a Historical Overview Greg Fasshauer Department of Applied Mathematics Illinois Institute of Technology Fall 2014 [email protected] MATH 590 – Chapter 1 1 Outline 1 Introduction 2 Some Historical Remarks [email protected] MATH 590 – Chapter 1 2 Introduction General Meshfree Methods Meshfree Methods have gained much attention in recent years interdisciplinary field many traditional numerical methods (finite differences, finite elements or finite volumes) have trouble with high-dimensional problems meshfree methods can often handle changes in the geometry of the domain of interest (e.g., free surfaces, moving particles and large deformations) better independence from a mesh is a great advantage since mesh generation is one of the most time consuming parts of any mesh-based numerical simulation new generation of numerical tools [email protected] MATH 590 – Chapter 1 4 Introduction General Meshfree Methods Applications Original applications were in geodesy, geophysics, mapping, or meteorology Later, many other application areas numerical solution of PDEs in many engineering applications, computer graphics, optics, artificial intelligence, machine learning or statistical learning (neural networks or SVMs), signal and image processing, sampling theory, statistics (kriging), response surface or surrogate modeling, finance, optimization. [email protected] MATH 590 – Chapter 1 5 Introduction General Meshfree Methods Complicated Domains Recent paradigm shift in numerical simulation of fluid -

A Meshless Approach to Solving Partial Differential Equations Using the Finite Cloud Method for the Purposes of Computer Aided Design
A Meshless Approach to Solving Partial Differential Equations Using the Finite Cloud Method for the Purposes of Computer Aided Design by Daniel Rutherford Burke, B.Eng A Thesis submitted to the Faculty of Graduate and Post Doctoral Affairs in partial fulfilment of the requirements for the degree of Doctor of Philosophy Ottawa Carleton Institute for Electrical and Computer Engineering Department of Electronics Carleton University Ottawa, Ontario, Canada January 2013 Library and Archives Bibliotheque et Canada Archives Canada Published Heritage Direction du 1+1 Branch Patrimoine de I'edition 395 Wellington Street 395, rue Wellington Ottawa ON K1A0N4 Ottawa ON K1A 0N4 Canada Canada Your file Votre reference ISBN: 978-0-494-94524-7 Our file Notre reference ISBN: 978-0-494-94524-7 NOTICE: AVIS: The author has granted a non L'auteur a accorde une licence non exclusive exclusive license allowing Library and permettant a la Bibliotheque et Archives Archives Canada to reproduce, Canada de reproduire, publier, archiver, publish, archive, preserve, conserve, sauvegarder, conserver, transmettre au public communicate to the public by par telecommunication ou par I'lnternet, preter, telecommunication or on the Internet, distribuer et vendre des theses partout dans le loan, distrbute and sell theses monde, a des fins commerciales ou autres, sur worldwide, for commercial or non support microforme, papier, electronique et/ou commercial purposes, in microform, autres formats. paper, electronic and/or any other formats. The author retains copyright L'auteur conserve la propriete du droit d'auteur ownership and moral rights in this et des droits moraux qui protege cette these. Ni thesis. Neither the thesis nor la these ni des extraits substantiels de celle-ci substantial extracts from it may be ne doivent etre imprimes ou autrement printed or otherwise reproduced reproduits sans son autorisation. -

A Plane Wave Method Based on Approximate Wave Directions for Two
A PLANE WAVE METHOD BASED ON APPROXIMATE WAVE DIRECTIONS FOR TWO DIMENSIONAL HELMHOLTZ EQUATIONS WITH LARGE WAVE NUMBERS QIYA HU AND ZEZHONG WANG Abstract. In this paper we present and analyse a high accuracy method for computing wave directions defined in the geometrical optics ansatz of Helmholtz equation with variable wave number. Then we define an “adaptive” plane wave space with small dimensions, in which each plane wave basis function is determined by such an approximate wave direction. We establish a best L2 approximation of the plane wave space for the analytic solutions of homogeneous Helmholtz equa- tions with large wave numbers and report some numerical results to illustrate the efficiency of the proposed method. Key words. Helmholtz equations, variable wave numbers, geometrical optics ansatz, approximate wave direction, plane wave space, best approximation AMS subject classifications. 65N30, 65N55. 1. Introduction In this paper we consider the following Helmholtz equation with impedance boundary condition u = (∆ + κ2(r))u(ω, r)= f(ω, r), r = (x, y) Ω, L − ∈ (1.1) ((∂n + iκ(r))u(ω, r)= g(ω, r), r ∂Ω, ∈ where Ω R2 is a bounded Lipchitz domain, n is the out normal vector on ∂Ω, ⊂ f L2(Ω) is the source term and κ(r) = ω , g L2(∂Ω). In applications, ω ∈ c(r) ∈ denotes the frequency and may be large, c(r) > 0 denotes the light speed, which is arXiv:2107.09797v1 [math.NA] 20 Jul 2021 usually a variable positive function. The number κ(r) is called the wave number. Helmholtz equation is the basic model in sound propagation. -
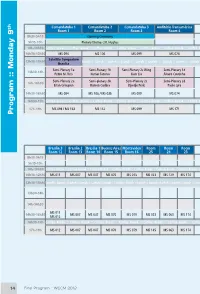
Program :: Monday 9
Comandatuba 1 Comandatuba 2 Comandatuba 3 Auditório Transamérica Una Ilhéus São Paulo 3 São Paulo 2 São Paulo 1 Quito Santiago th Room 1 Room 2 Room 3 Room 4 Room 5 Room 6 Room 7 Room 8 Room 9 Room 10 Room 11 8h30-9h15 Opening Ceremony 9h15-10h Plenary Thomas J.R. Hughes 10h-10h30 Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break 10h30-12h30 MS 094 MS 106 MS 099 MS 074 MS 142 MS 133 MS 001 MS 075 MS 085 MS 002 Satellite Symposium 12h30-13h30 Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch Brasília Semi-Plenary 1a Semi-Plenary 1b Semi-Plenary 2c Wing Semi-Plenary 1d 13h30-14h Pedro M. Reis Kumar Tamma Kam Liu Álvaro Coutinho Semi-Plenary 2a Semi-plenary 2b Semi-Plenary 2c Semi-Plenary 2d 14h-14h30 Eitan Grinspun Ramon Codina Djordje Peric Paulo Lyra 14h30-16h30 MS 094 MS 106 / MS 035 MS 099 MS 074 MS 142 MS 133 MS 001 MS 075 MS 085 MS 002 16h30-17h Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break 17h-19h MS 094 / MS 163 MS 132 MS 099 MS 171 MS 142 / MS 005 MS 116 MS 001 MS 075 MS 085 MS 002 Program :: Monday 9 Brasília 3 Brasília 2 Brasília 1 Buenos Aires Montevideo Room Room Room Room Room Room Room Room -

14Th U.S. National Congress on Computational Mechanics
14th U.S. National Congress on Computational Mechanics Montréal • July 17-20, 2017 Congress Program at a Glance Sunday, July 16 Monday, July 17 Tuesday, July 18 Wednesday, July 19 Thursday, July 20 Registration Registration Registration Registration Short Course 7:30 am - 5:30 pm 7:30 am - 5:30 pm 7:30 am - 5:30 pm 7:30 am - 11:30 am Registration 8:00 am - 9:30 am 8:30 am - 9:00 am OPENING PL: Tarek Zohdi PL: Andrew Stuart PL: Mark Ainsworth PL: Anthony Patera 9:00 am - 9.45 am Chair: J.T. Oden Chair: T. Hughes Chair: L. Demkowicz Chair: M. Paraschivoiu Short Courses 9:45 am - 10:15 am Coffee Break Coffee Break Coffee Break Coffee Break 9:00 am - 12:00 pm 10:15 am - 11:55 am Technical Session TS1 Technical Session TS4 Technical Session TS7 Technical Session TS10 Lunch Break 11:55 am - 1:30 pm Lunch Break Lunch Break Lunch Break CLOSING aSPL: Raúl Tempone aSPL: Ron Miller aSPL: Eldad Haber 1:30 pm - 2:15 pm bSPL: Marino Arroyo bSPL: Beth Wingate bSPL: Margot Gerritsen Short Courses 2:15 pm - 2:30 pm Break-out Break-out Break-out 1:00 pm - 4:00 pm 2:30 pm - 4:10 pm Technical Session TS2 Technical Session TS5 Technical Session TS8 4:10 pm - 4:40 pm Coffee Break Coffee Break Coffee Break Congress Registration 2:00 pm - 8:00 pm 4:40 pm - 6:20 pm Technical Session TS3 Poster Session TS6 Technical Session TS9 Reception Opening in 517BC Cocktail Coffee Breaks in 517A 7th floor Terrace Plenary Lectures (PL) in 517BC 7:00 pm - 7:30 pm Cocktail and Banquet 6:00 pm - 8:00 pm Semi-Plenary Lectures (SPL): Banquet in 517BC aSPL in 517D 7:30 pm - 9:30 pm Viewing of Fireworks bSPL in 516BC Fireworks and Closing Reception Poster Session in 517A 10:00 pm - 10:30 pm on 7th floor Terrace On behalf of Polytechnique Montréal, it is my pleasure to welcome, to Montreal, the 14th U.S. -

Family Name Given Name Presentation Title Session Code
Family Name Given Name Presentation Title Session Code Abdoulaev Gassan Solving Optical Tomography Problem Using PDE-Constrained Optimization Method Poster P Acebron Juan Domain Decomposition Solution of Elliptic Boundary Value Problems via Monte Carlo and Quasi-Monte Carlo Methods Formulations2 C10 Adams Mark Ultrascalable Algebraic Multigrid Methods with Applications to Whole Bone Micro-Mechanics Problems Multigrid C7 Aitbayev Rakhim Convergence Analysis and Multilevel Preconditioners for a Quadrature Galerkin Approximation of a Biharmonic Problem Fourth-order & ElasticityC8 Anthonissen Martijn Convergence Analysis of the Local Defect Correction Method for 2D Convection-diffusion Equations Flows C3 Bacuta Constantin Partition of Unity Method on Nonmatching Grids for the Stokes Equations Applications1 C9 Bal Guillaume Some Convergence Results for the Parareal Algorithm Space-Time ParallelM5 Bank Randolph A Domain Decomposition Solver for a Parallel Adaptive Meshing Paradigm Plenary I6 Barbateu Mikael Construction of the Balancing Domain Decomposition Preconditioner for Nonlinear Elastodynamic Problems Balancing & FETIC4 Bavestrello Henri On Two Extensions of the FETI-DP Method to Constrained Linear Problems FETI & Neumann-NeumannM7 Berninger Heiko On Nonlinear Domain Decomposition Methods for Jumping Nonlinearities Heterogeneities C2 Bertoluzza Silvia The Fully Discrete Fat Boundary Method: Optimal Error Estimates Formulations2 C10 Biros George A Survey of Multilevel and Domain Decomposition Preconditioners for Inverse Problems in Time-dependent -

Analysis-Guided Improvements of the Material Point Method
ANALYSIS-GUIDED IMPROVEMENTS OF THE MATERIAL POINT METHOD by Michael Dietel Steffen A dissertation submitted to the faculty of The University of Utah in partial fulfillment of the requirements for the degree of Doctor of Philosophy in Computing School of Computing The University of Utah December 2009 Copyright c Michael Dietel Steffen 2009 ° All Rights Reserved THE UNIVERSITY OF UTAH GRADUATE SCHOOL SUPERVISORY COMMITTEE APPROVAL of a dissertation submitted by Michael Dietel Steffen This dissertation has been read by each member of the following supervisory committee and by majority vote has been found to be satisfactory. Chair: Robert M. Kirby Martin Berzins Christopher R. Johnson Steven G. Parker James E. Guilkey THE UNIVERSITY OF UTAH GRADUATE SCHOOL FINAL READING APPROVAL To the Graduate Council of the University of Utah: I have read the dissertation of Michael Dietel Steffen in its final form and have found that (1) its format, citations, and bibliographic style are consistent and acceptable; (2) its illustrative materials including figures, tables, and charts are in place; and (3) the final manuscript is satisfactory to the Supervisory Committee and is ready for submission to The Graduate School. Date Robert M. Kirby Chair, Supervisory Committee Approved for the Major Department Martin Berzins Chair/Dean Approved for the Graduate Council Charles A. Wight Dean of The Graduate School ABSTRACT The Material Point Method (MPM) has shown itself to be a powerful tool in the simulation of large deformation problems, especially those involving complex geometries and contact where typical finite element type methods frequently fail. While these large complex problems lead to some impressive simulations and so- lutions, there has been a lack of basic analysis characterizing the errors present in the method, even on the simplest of problems. -

(PFEM) for Solid Mechanics
Development and preliminary evaluation of the main features of the Particle Finite Element Method (PFEM) for solid mechanics Vasilis Papakrivopoulos Development and preliminary evaluation of the main features of the Particle Finite Element Method (PFEM) for solid mechanics by Vasilis Papakrivopoulos to obtain the degree of Master of Science at the Delft University of Technology, to be defended publicly on Monday December 10, 2018 at 2:00 PM. Student number: 4632567 Project duration: February 15, 2018 – December 10, 2018 Thesis committee: Dr. P.J.Vardon, TU Delft (chairman) Prof. dr. M.A. Hicks, TU Delft Dr. F.Pisanò, TU Delft J.L. Gonzalez Acosta, MSc, TU Delft (daily supervisor) An electronic version of this thesis is available at http://repository.tudelft.nl/. PREFACE This work concludes my academic career in the Technical University of Delft and marks the end of my stay in this beautiful town. During the two-year period of my master stud- ies I managed to obtain experiences and strengthen the theoretical background in the civil engineering field that was founded through my studies in the National Technical University of Athens. I was given the opportunity to come across various interesting and challenging topics, with this current project being the highlight of this course, and I was also able to slowly but steadily integrate into the Dutch society. In retrospect, I feel that I have made the right choice both personally and career-wise when I decided to move here and study in TU Delft. At this point, I would like to thank the graduation committee of my master thesis. -

Combined FEM/Meshfree SPH Method for Impact Damage Prediction of Composite Sandwich Panels
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Institute of Transport Research:Publications ECCOMAS Thematic Conference on Meshless Methods 2005 1 Combined FEM/Meshfree SPH Method for Impact Damage Prediction of Composite Sandwich Panels L.Aktay(1), A.F.Johnson(2) and B.-H.Kroplin¨ (3) Abstract: In this work, impact simulations using both meshfree Smoothed Particle Hy- drodynamics (SPH) and combined FEM/SPH Method were carried out for a sandwich composite panel with carbon fibre fabric/epoxy face skins and polyetherimide (PEI) foam core. A numerical model was developed using the dynamic explicit finite element (FE) structure analysis program PAM-CRASH. The carbon fibre/epoxy facings were modelled with standard layered shell elements, whilst SPH particles were positioned for the PEI core. We demonstrate the efficiency and the advantages of pure meshfree SPH and com- bined FEM/SPH Method by comparing the core deformation modes and impact force pulses measured in the experiments to predict structural impact response. Keywords: Impact damage, composite material, sandwich structure concept, Finite Ele- ment Method (FEM), meshfree method, Smoothed Particle Hydrodynamics (SPH) 1 Introduction Modelling of high velocity impact (HVI) and crash scenarios involving material failure and large deformation using classical FEM is complex. Although the most popular numer- ical method FEM is still an effective tool in predicting the structural behaviour in different loading conditions, FEM suffers from large deformation leading problems causing con- siderable accuracy lost. Additionally it is very difficult to simulate the structural behaviour containing the breakage of material into large number of fragments since FEM is initially based on continuum mechanics requiring critical element connectivity. -

Overview of Meshless Methods
Technical Article Overview of Meshless Methods Abstract— This article presents an overview of the main develop- ments of the mesh-free idea. A review of the main publications on the application of the meshless methods in Computational Electromagnetics is also given. I. INTRODUCTION Several meshless methods have been proposed over the last decade. Although these methods usually all bear the generic label “meshless”, not all are truly meshless. Some, such as those based on the Collocation Point technique, have no associated mesh but others, such as those based on the Galerkin method, actually do Fig. 1. EFG background cell structure. require an auxiliary mesh or cell structure. At the time of writing, the authors are not aware of any proposed formal classification of these techniques. This paper is therefore not concerned with any C. The Element-Free Galerkin (EFG) classification of these methods, instead its objective is to present In 1994 Belytschko and colleagues introduced the Element-Free an overview of the main developments of the mesh-free idea, Galerkin Method (EFG) [8], an extended version of Nayroles’s followed by a review of the main publications on the application method. The Element-Free Galerkin introduced a series of im- of meshless methods to Computational Electromagnetics. provements over the Diffuse Element Method formulation, such as II. MESHLESS METHODS -THE HISTORY • Proper determination of the approximation derivatives: A. The Smoothed Particle Hydrodynamics In DEM the derivatives of the approximation function The advent of the mesh free idea dates back from 1977, U h are obtained by considering the coefficients b of the with Monaghan and Gingold [1] and Lucy [2] developing a polynomial basis p as constants, such that Lagrangian method based on the Kernel Estimates method to h T model astrophysics problems. -

Scalable Large-Scale Fluid-Structure Interaction Solvers in the Uintah Framework Via Hybrid Task-Based Parallelism Algorithms
1 Scalable Large-scale Fluid-structure Interaction Solvers in the Uintah Framework via Hybrid Task-based Parallelism Algorithms Qingyu Meng, Martin Berzins UUSCI-2012-004 Scientific Computing and Imaging Institute University of Utah Salt Lake City, UT 84112 USA May 7, 2012 Abstract: Uintah is a software framework that provides an environment for solving fluid-structure interaction problems on structured adaptive grids on large-scale science and engineering problems involving the solution of partial differential equations. Uintah uses a combination of fluid-flow solvers and particle-based methods for solids, together with adaptive meshing and a novel asynchronous task-based approach with fully automated load balancing. When applying Uintah to fluid-structure interaction problems with mesh refinement, the combination of adaptive meshing and the move- ment of structures through space present a formidable challenge in terms of achieving scalability on large-scale parallel computers. With core counts per socket continuing to grow along with the prospect of less memory per core, adopting a model that uses MPI to communicate between nodes and a shared memory model on-node is one approach to achieve scalability at full machine capacity on current and emerging large-scale systems. For this approach to be successful, it is necessary to design data-structures that large numbers of cores can simultaneously access without contention. These data structures and algorithms must also be designed to avoid the overhead involved with locks and other synchronization primitives when running on large number of cores per node, as contention for acquiring locks quickly becomes untenable. This scalability challenge is addressed here for Uintah, by the development of new hybrid runtime and scheduling algorithms combined with novel lockfree data structures, making it possible for Uintah to achieve excellent scalability for a challenging fluid-structure problem with mesh refinement on as many as 260K cores. -

The Material-Point Method for Granular Materials
Comput. Methods Appl. Mech. Engrg. 187 (2000) 529±541 www.elsevier.com/locate/cma The material-point method for granular materials S.G. Bardenhagen a, J.U. Brackbill b,*, D. Sulsky c a ESA-EA, MS P946 Los Alamos National Laboratory, Los Alamos, NM 87545, USA b T-3, MS B216 Los Alamos National Laboratory, Los Alamos, NM 87545, USA c Department of Mathematics and Statistics, University of New Mexico, Albuquerqe, NM 87131, USA Abstract A model for granular materials is presented that describes both the internal deformation of each granule and the interactions between grains. The model, which is based on the FLIP-material point, particle-in-cell method, solves continuum constitutive models for each grain. Interactions between grains are calculated with a contact algorithm that forbids interpenetration, but allows separation and sliding and rolling with friction. The particle-in-cell method eliminates the need for a separate contact detection step. The use of a common rest frame in the contact model yields a linear scaling of the computational cost with the number of grains. The properties of the model are illustrated by numerical solutions of sliding and rolling contacts, and for granular materials by a shear calculation. The results of numerical calculations demonstrate that contacts are modeled accurately for smooth granules whose shape is resolved by the computation mesh. Ó 2000 Elsevier Science S.A. All rights reserved. 1. Introduction Granular materials are large conglomerations of discrete macroscopic particles, which may slide against one another but not penetrate [9]. Like a liquid, granular materials can ¯ow to assume the shape of the container.