Richard Courant 1888–1972
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
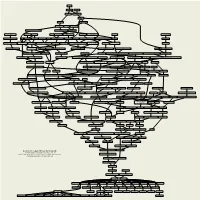
Academic Genealogy of George Em Karniadakis
Nilos Kabasilas Demetrios Kydones Elissaeus Judaeus Manuel Chrysoloras Georgios Plethon Gemistos 1380, 1393 Basilios Bessarion 1436 Mystras Guarino da Verona Johannes Argyropoulos 1408 1444 Università di Padova Vittorino da Feltre Cristoforo Landino Marsilio Ficino 1416 Università di Padova 1462 Università di Firenze Ognibene (Omnibonus Leonicenus) Bonisoli da Lonigo Theodoros Gazes Angelo Poliziano Università di Mantova 1433 Constantinople / Università di Mantova 1477 Università di Firenze Leo Outers Alessandro Sermoneta Gaetano da Thiene Moses Perez Scipione Fortiguerra Demetrios Chalcocondyles Jacob ben Jehiel Loans Rudolf Agricola Thomas à Kempis Heinrich von Langenstein 1485 Université Catholique de Louvain 1493 Università di Firenze 1452 Mystras / Accademia Romana 1478 Università degli Studi di Ferrara 1363, 1375 Université de Paris Maarten (Martinus Dorpius) van Dorp Pelope Pietro Roccabonella Nicoletto Vernia François Dubois Jean Tagault Girolamo (Hieronymus Aleander) Aleandro Janus Lascaris Matthaeus Adrianus Johann (Johannes Kapnion) Reuchlin Jan Standonck Alexander Hegius Johannes von Gmunden 1504, 1515 Université Catholique de Louvain Università di Padova Università di Padova 1516 Université de Paris 1499, 1508 Università di Padova 1472 Università di Padova 1477, 1481 Universität Basel / Université de Poitiers 1474, 1490 Collège Sainte-Barbe / Collège de Montaigu 1474 1406 Universität Wien Niccolò Leoniceno Jacobus (Jacques Masson) Latomus Desiderius Erasmus Petrus (Pieter de Corte) Curtius Pietro Pomponazzi Jacobus (Jacques -

Mathematics People
Mathematics People symmetric spaces, L²-cohomology, arithmetic groups, and MacPherson Awarded Hopf the Langlands program. The list is by far not complete, and Prize we try only to give a representative selection of his contri- bution to mathematics. He influenced a whole generation Robert MacPherson of the Institute for Advanced Study of mathematicians by giving them new tools to attack has been chosen the first winner of the Heinz Hopf Prize difficult problems and teaching them novel geometric, given by ETH Zurich for outstanding scientific work in the topological, and algebraic ways of thinking.” field of pure mathematics. MacPherson, a leading expert Robert MacPherson was born in 1944 in Lakewood, in singularities, delivered the Heinz Hopf Lectures, titled Ohio. He received his B.A. from Swarthmore College in “How Nature Tiles Space”, in October 2009. The prize also 1966 and his Ph.D. from Harvard University in 1970. He carries a cash award of 30,000 Swiss francs, approximately taught at Brown University from 1970 to 1987 and at equal to US$30,000. the Massachusetts Institute of Technology from 1987 to The following quotation was taken from a tribute to 1994. He has been at the Institute for Advanced Study in MacPherson by Gisbert Wüstholz of ETH Zurich: “Singu- Princeton since 1994. His work has introduced radically larities can be studied in different ways using analysis, new approaches to the topology of singular spaces and or you can regard them as geometric phenomena. For the promoted investigations across a great spectrum of math- latter, their study demands a deep geometric intuition ematics. -

Hilbert Constance Reid
Hilbert Constance Reid Hilbert c COPERNICUS AN IMPRINT OF SPRINGER-VERLAG © 1996 Springer Science+Business Media New York Originally published by Springer-Verlag New York, Inc in 1996 All rights reserved. No part ofthis publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, recording, or otherwise, without the prior written permission of the publisher. Library ofCongress Cataloging·in-Publication Data Reid, Constance. Hilbert/Constance Reid. p. Ctn. Originally published: Berlin; New York: Springer-Verlag, 1970. Includes bibliographical references and index. ISBN 978-0-387-94674-0 ISBN 978-1-4612-0739-9 (eBook) DOI 10.1007/978-1-4612-0739-9 I. Hilbert, David, 1862-1943. 2. Mathematicians-Germany Biography. 1. Title. QA29.HsR4 1996 SIO'.92-dc20 [B] 96-33753 Manufactured in the United States of America. Printed on acid-free paper. 9 8 7 6 543 2 1 ISBN 978-0-387-94674-0 SPIN 10524543 Questions upon Rereading Hilbert By 1965 I had written several popular books, such as From liro to Infinity and A Long Way from Euclid, in which I had attempted to explain certain easily grasped, although often quite sophisticated, mathematical ideas for readers very much like myself-interested in mathematics but essentially untrained. At this point, with almost no mathematical training and never having done any bio graphical writing, I became determined to write the life of David Hilbert, whom many considered the profoundest mathematician of the early part of the 20th century. Now, thirty years later, rereading Hilbert, certain questions come to my mind. -

History of Mathematics in Mathematics Education. Recent Developments Kathy Clark, Tinne Kjeldsen, Sebastian Schorcht, Constantinos Tzanakis, Xiaoqin Wang
History of mathematics in mathematics education. Recent developments Kathy Clark, Tinne Kjeldsen, Sebastian Schorcht, Constantinos Tzanakis, Xiaoqin Wang To cite this version: Kathy Clark, Tinne Kjeldsen, Sebastian Schorcht, Constantinos Tzanakis, Xiaoqin Wang. History of mathematics in mathematics education. Recent developments. History and Pedagogy of Mathematics, Jul 2016, Montpellier, France. hal-01349230 HAL Id: hal-01349230 https://hal.archives-ouvertes.fr/hal-01349230 Submitted on 27 Jul 2016 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. HISTORY OF MATHEMATICS IN MATHEMATICS EDUCATION Recent developments Kathleen CLARK, Tinne Hoff KJELDSEN, Sebastian SCHORCHT, Constantinos TZANAKIS, Xiaoqin WANG School of Teacher Education, Florida State University, Tallahassee, FL 32306-4459, USA [email protected] Department of Mathematical Sciences, University of Copenhagen, Denmark [email protected] Justus Liebig University Giessen, Germany [email protected] Department of Education, University of Crete, Rethymnon 74100, Greece [email protected] Department of Mathematics, East China Normal University, China [email protected] ABSTRACT This is a survey on the recent developments (since 2000) concerning research on the relations between History and Pedagogy of Mathematics (the HPM domain). Section 1 explains the rationale of the study and formulates the key issues. -

German Jews in the United States: a Guide to Archival Collections
GERMAN HISTORICAL INSTITUTE,WASHINGTON,DC REFERENCE GUIDE 24 GERMAN JEWS IN THE UNITED STATES: AGUIDE TO ARCHIVAL COLLECTIONS Contents INTRODUCTION &ACKNOWLEDGMENTS 1 ABOUT THE EDITOR 6 ARCHIVAL COLLECTIONS (arranged alphabetically by state and then city) ALABAMA Montgomery 1. Alabama Department of Archives and History ................................ 7 ARIZONA Phoenix 2. Arizona Jewish Historical Society ........................................................ 8 ARKANSAS Little Rock 3. Arkansas History Commission and State Archives .......................... 9 CALIFORNIA Berkeley 4. University of California, Berkeley: Bancroft Library, Archives .................................................................................................. 10 5. Judah L. Mages Museum: Western Jewish History Center ........... 14 Beverly Hills 6. Acad. of Motion Picture Arts and Sciences: Margaret Herrick Library, Special Coll. ............................................................................ 16 Davis 7. University of California at Davis: Shields Library, Special Collections and Archives ..................................................................... 16 Long Beach 8. California State Library, Long Beach: Special Collections ............. 17 Los Angeles 9. John F. Kennedy Memorial Library: Special Collections ...............18 10. UCLA Film and Television Archive .................................................. 18 11. USC: Doheny Memorial Library, Lion Feuchtwanger Archive ................................................................................................... -

Emil Artin in America
MATHEMATICAL PERSPECTIVES BULLETIN (New Series) OF THE AMERICAN MATHEMATICAL SOCIETY Volume 50, Number 2, April 2013, Pages 321–330 S 0273-0979(2012)01398-8 Article electronically published on December 18, 2012 CREATING A LIFE: EMIL ARTIN IN AMERICA DELLA DUMBAUGH AND JOACHIM SCHWERMER 1. Introduction In January 1933, Adolf Hitler and the Nazi party assumed control of Germany. On 7 April of that year the Nazis created the notion of “non-Aryan descent”.1 “It was only a question of time”, Richard Brauer would later describe it, “until [Emil] Artin, with his feeling for individual freedom, his sense of justice, his abhorrence of physical violence would leave Germany” [5, p. 28]. By the time Hitler issued the edict on 26 January 1937, which removed any employee married to a Jew from their position as of 1 July 1937,2 Artin had already begun to make plans to leave Germany. Artin had married his former student, Natalie Jasny, in 1929, and, since she had at least one Jewish grandparent, the Nazis classified her as Jewish. On 1 October 1937, Artin and his family arrived in America [19, p. 80]. The surprising combination of a Roman Catholic university and a celebrated American mathematician known for his gnarly personality played a critical role in Artin’s emigration to America. Solomon Lefschetz had just served as AMS president from 1935–1936 when Artin came to his attention: “A few days ago I returned from a meeting of the American Mathematical Society where as President, I was particularly well placed to know what was going on”, Lefschetz wrote to the president of Notre Dame on 12 January 1937, exactly two weeks prior to the announcement of the Hitler edict that would influence Artin directly. -

Constance Reid
Constance Reid John Ewing, former director of the American Mathematical Society, says this of Constance Reid: “ She has a special talent for understanding mathematicians and their culture. She understands us. She is the Boswell for mathematics – a biographer who has made the mathematical life understandable to the general public and to mathematicians themselves. Her work has enriched our profession.” The “autobiography” of her sister Julia Robinson has been a source of inspiration for many young women contemplating careers in mathematics, and her biography of David Hilbert stands as one of the best mathematical biographies ever written. It is no exaggeration to say that publication of Hilbert made her a star among mathematical biographers. Her five lively and penetrating biographies of mathematicians have been highly praised and constitute a great contribution to the world of mathematics. She has set a high standard for future biographers. We are proud that she was a member of our section. Although the formal mathematical education of Constance Reid concluded with high school algebra and geometry, she was able to understand mathematical ideas well enough to write three best - selling popularizations of mathematics: From Zero to Infinity (1955), Introduction to Higher Mathematics (1959), and A Long Way From Euclid (1963). Several mathematicians have commented on the influence of From Zero to Infinity on their development. Her writing ability was early demonstrated in her book Slacks and Calluses(1944), an account of her working for a summer on a bomber factory assembly line in World War II. At the time she was a high school English teacher in San Diego and only twenty - six. -

Classics in Mathematics Richard Courant· Fritz John Introduction To
Classics in Mathematics Richard Courant· Fritz John Introduction to Calculus and Analysis Volume I Springer-V erlag Berlin Heidelberg GmbH Richard Courant • Fritz John Introd uction to Calculus and Analysis Volume I Reprint of the 1989 Edition Springer Originally published in 1965 by Interscience Publishers, a division of John Wiley and Sons, Inc. Reprinted in 1989 by Springer-Verlag New York, Inc. Mathematics Subject Classification (1991): 26-XX, 26-01 Cataloging in Publication Data applied for Die Deutsche Bibliothek - CIP-Einheitsaufnahme Courant, Richard: Introduction to calcu1us and analysis / Richard Courant; Fritz John.- Reprint of the 1989 ed.- Berlin; Heidelberg; New York; Barcelona; Hong Kong; London; Milan; Paris; Singapore; Tokyo: Springer (Classics in mathematics) VoL 1 (1999) ISBN 978-3-540-65058-4 ISBN 978-3-642-58604-0 (eBook) DOI 10.1007/978-3-642-58604-0 Photograph of Richard Courant from: C. Reid, Courant in Gottingen and New York. The Story of an Improbable Mathematician, Springer New York, 1976 Photograph of Fritz John by kind permission of The Courant Institute of Mathematical Sciences, New York ISSN 1431-0821 This work is subject to copyright. All rights are reserved. whether the whole or part of the material is concemed. specifically the rights of trans1ation. reprinting. reuse of illustrations. recitation. broadcasting. reproduction on microfilm or in any other way. and storage in data banks. Duplication of this publication or parts thereof is permitted onlyunder the provisions of the German Copyright Law of September 9.1965. in its current version. and permission for use must always be obtained from Springer-Verlag. Violations are Iiable for prosecution under the German Copyright Law. -

A Century of Mathematics in America, Peter Duren Et Ai., (Eds.), Vol
Garrett Birkhoff has had a lifelong connection with Harvard mathematics. He was an infant when his father, the famous mathematician G. D. Birkhoff, joined the Harvard faculty. He has had a long academic career at Harvard: A.B. in 1932, Society of Fellows in 1933-1936, and a faculty appointmentfrom 1936 until his retirement in 1981. His research has ranged widely through alge bra, lattice theory, hydrodynamics, differential equations, scientific computing, and history of mathematics. Among his many publications are books on lattice theory and hydrodynamics, and the pioneering textbook A Survey of Modern Algebra, written jointly with S. Mac Lane. He has served as president ofSIAM and is a member of the National Academy of Sciences. Mathematics at Harvard, 1836-1944 GARRETT BIRKHOFF O. OUTLINE As my contribution to the history of mathematics in America, I decided to write a connected account of mathematical activity at Harvard from 1836 (Harvard's bicentennial) to the present day. During that time, many mathe maticians at Harvard have tried to respond constructively to the challenges and opportunities confronting them in a rapidly changing world. This essay reviews what might be called the indigenous period, lasting through World War II, during which most members of the Harvard mathe matical faculty had also studied there. Indeed, as will be explained in §§ 1-3 below, mathematical activity at Harvard was dominated by Benjamin Peirce and his students in the first half of this period. Then, from 1890 until around 1920, while our country was becoming a great power economically, basic mathematical research of high quality, mostly in traditional areas of analysis and theoretical celestial mechanics, was carried on by several faculty members. -

Notices of the American Mathematical
OF THE AMERICAN MATHEMATICAL SOCIETY VOLUMf 12, NUMBER 2 ISSUE NO. 80 FEBRUARY 1965 cNotiaiJ OF THE AMERICAN MATHEMATICAL SOCIETY Edited by John W. Green and Gordon L. \Yalker CONTENTS MEETINGS Calendar of Meetings o o o o o o o o o • o o • o o o o o o o • o 0 o 0 o 0 • 0 • 0 0 • 0 0 184 Program of the Meeting in New York. o 0 o 0 o 0 0 • 0 o o o 0 0 0 0 • 0 0 0 0 0 • 185 Abstracts for the Meeting- Pages 209-216 PRELIMINARY ANNOUNCEMENTS OF MEETINGS • o o o o o o o o • o 0 • 0 • 0 • • • 188 ACTIVITIES OF OTHER ASSOCIATIONS •••• o o. o o o o • o o o •• o 0 0 0. o 0 0 0 0 191 LETTERS TO THE EDITOR • o ••••• o o • o o o o o • o ••• o •••• o o o •• o o • o o 192 MEMORANDA TO MEMBERS List of Retired Mathematicians 190 Increase in Page Charges o o ••• o •• o • o o o •••••• 0 ••• 0 0 0 •• 0 0 0 0 194 Journals in Microform • o •••• o 0 ••• o • o ••• 0 •• o ••••• 0 •• 0 • • • • 194 Backlog of Mathematics Research Journals 0 0 0. 0. 0 ••• 0 •• 0 •• 0.. 195 Corporate Members ••••••••••••• 0 • 0 0 0 0 •• 0 0 • 0 •• 0 0 •• 0 ••• 0 201 ASSISTANTSHIPS AND FELLOWSHIPS IN MATHEMATICS 1965-1966 0 ••• 0 • 0 196 NEW AMS PUBLICATIONS • o •• o •• o •••• o • o o ••••• o o o •• o o •• o • o • o • 197 PERSONAL ITEMS .••••• o •• o. -

Writing the History of Dynamical Systems and Chaos
Historia Mathematica 29 (2002), 273–339 doi:10.1006/hmat.2002.2351 Writing the History of Dynamical Systems and Chaos: View metadata, citation and similar papersLongue at core.ac.uk Dur´ee and Revolution, Disciplines and Cultures1 brought to you by CORE provided by Elsevier - Publisher Connector David Aubin Max-Planck Institut fur¨ Wissenschaftsgeschichte, Berlin, Germany E-mail: [email protected] and Amy Dahan Dalmedico Centre national de la recherche scientifique and Centre Alexandre-Koyre,´ Paris, France E-mail: [email protected] Between the late 1960s and the beginning of the 1980s, the wide recognition that simple dynamical laws could give rise to complex behaviors was sometimes hailed as a true scientific revolution impacting several disciplines, for which a striking label was coined—“chaos.” Mathematicians quickly pointed out that the purported revolution was relying on the abstract theory of dynamical systems founded in the late 19th century by Henri Poincar´e who had already reached a similar conclusion. In this paper, we flesh out the historiographical tensions arising from these confrontations: longue-duree´ history and revolution; abstract mathematics and the use of mathematical techniques in various other domains. After reviewing the historiography of dynamical systems theory from Poincar´e to the 1960s, we highlight the pioneering work of a few individuals (Steve Smale, Edward Lorenz, David Ruelle). We then go on to discuss the nature of the chaos phenomenon, which, we argue, was a conceptual reconfiguration as -

Women's History Magazine Broadly As Possible
Women’s History Magazine Issue 48, AUTUMN 2004 Issn 1476-6760 Themed Issue: Science, Technology and Education Maria Rentetzi on The Case of the Radium Dial Painters Claire Jones on Grace Chisholm Young in Turn-of-Nineteenth-Century Germany Joyce Goodman on Technical Education, Female Emigration and Nation Building Hull 2004 Conference Report Launch of new WHN Book Prize Clare Evans Prize — Report on 2004 Award and Hypatia Announcement of of Alexandria 2005 Competition c. 370 - 415 Conference 2005 — Mathematician philosopher, Call for Papers teacher and inventor of mechanical devices. th 14 Conference of the Women’s History Network Women, Art and Culture: Historical Perspectives September 2nd- 4th 2005, Southampton Southampton Institute, Sir James Matthews Conference Centre, Southampton, Hants. Papers are welcomed on the following themes: Women and the visual arts; painting, sculpture, architecture, and the decorative arts. Women and the Arts and Crafts Movement/Home Decorating. Women and the performing arts. Women and the literary arts. Women as art objects/images of women. Women as mediators of culture. Women as collectors and benefactors. Plenary Speakers: Frances Borzello on 'Women Artists: Self Portraits' Marina Vaizey on '20th Century Women Collectors' Speakers, papers and a provisional programme will be posted at www.womenshistorynetwork.org as soon as they become available. Papers will be considered for special issues of: Women’s History Magazine & Women’s History Review. Abstracts of 200-300 words should be sent by 30/03/05 to: Dr Anne Anderson, FMAS, Southampton Institute, Southampton, S014 ORF. [email protected] Administrator: Dr. Joyce A. Walker (Women’s History Network) , Department of History, University of Aberdeen, Crombie Annexe, Meston Walk, Old Aberdeen, AB24 3FX E-mail: [email protected] The arrival of this Autumn's Women's History Magazine broadly as possible.