Experiments on the Random Packing of Tetrahedral Dice
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Mutant Standard PUA Encoding Reference 0.3.1 (October 2018)
Mutant Standard PUA Encoding Reference 0.3.1 (October 2018) Mutant Standard’s PUA codepoints start at block 16 in Plane 10 Codepoint that Codepoint that New codepoint has existed has been given (SPUA-B) - U+1016xx, and will continue into the next blocks (1017xx, This document is licensed under a Creative Commons before this wording changes version this version 1018xx, etc.) if necessary. Attribution-ShareAlike 4.0 International License. Every Mutant Standard PUA encoding automatically assumes full- The data contained this document (ie. encodings, emoji descriptions) however, can be used in whatever way you colour emoji representations, so Visibility Selector 16 (U+FE0F) is like. not appropriate or necessary for any of these. Comments 0 1 2 3 4 5 6 7 8 9 A B C D E F Shared CMs 1 1016 0 Color Modifier Color Modifier Color Modifier Color Modifier Color Modifier Color Modifier Color Modifier Color Modifier Color Modifier Color Modifier Color Modifier Color Modifier Color Modifier Color Modifier Color Modifier Color Modifier R1 (dark red) R2 (red) R3 (light red) D1 (dark red- D2 (red-orange) D3 (light red- O1 (dark O2 (orange) O3 (light Y1 (dark yellow) Y2 (yellow) Y3 (light L1 (dark lime) L2 (lime) L3 (light lime) G1 (dark green) orange) orange) orange) orange) yellow) Shared CMs 2 1016 1 Color Modifier Color Modifier Color Modifier Color Modifier Color Modifier Color Modifier Color Modifier Color Modifier Color Modifier Color Modifier Color Modifier Color Modifier Color Modifier Color Modifier Color Modifier Color Modifier G2 (green) G3 (light green) T1 (dark teal) T2 (teal) -
![Arxiv:1603.05202V1 [Math.MG] 16 Mar 2016 Etr .Itrue Peia Amnc 27 Harmonics Spherical Interlude: 3](https://docslib.b-cdn.net/cover/2521/arxiv-1603-05202v1-math-mg-16-mar-2016-etr-itrue-peia-amnc-27-harmonics-spherical-interlude-3-512521.webp)
Arxiv:1603.05202V1 [Math.MG] 16 Mar 2016 Etr .Itrue Peia Amnc 27 Harmonics Spherical Interlude: 3
Contents Packing, coding, and ground states Henry Cohn 1 Packing, coding, and ground states 3 Preface 3 Acknowledgments 3 Lecture 1. Sphere packing 5 1. Introduction 5 2. Motivation 6 3. Phenomena 8 4. Constructions 10 5. Difficulty of sphere packing 12 6. Finding dense packings 13 7. Computational problems 15 Lecture 2. Symmetry and ground states 17 1. Introduction 17 2. Potential energy minimization 18 3. Families and universal optimality 19 4. Optimality of simplices 23 Lecture 3. Interlude: Spherical harmonics 27 1. Fourier series 27 2. Fourier series on a torus 29 3. Spherical harmonics 31 Lecture4. Energyandpackingboundsonspheres 35 arXiv:1603.05202v1 [math.MG] 16 Mar 2016 1. Introduction 35 2. Linear programming bounds 37 3. Applying linear programming bounds 39 4. Spherical codes and the kissing problem 40 5. Ultraspherical polynomials 41 Lecture 5. Packing bounds in Euclidean space 47 1. Introduction 47 2. Poisson summation 49 3. Linear programming bounds 50 4. Optimization and conjectures 52 Bibliography 57 i Packing, coding, and ground states Henry Cohn Packing, coding, and ground states Henry Cohn Preface In these lectures, we’ll study simple models of materials from several different perspectives: geometry (packing problems), information theory (error-correcting codes), and physics (ground states of interacting particle systems). These per- spectives each shed light on some of the same problems and phenomena, while highlighting different techniques and connections. One noteworthy phenomenon is the exceptional symmetry that is found in certain special cases, and we’ll examine when and why it occurs. The overall theme of the lectures is thus order vs. -

Of Dice and Men the Role of Dice in Board and Table Games
Homo Ludens 1/(2) (2010) Homo Ludens Of Dice and Men The role of dice in board and table games Jens Jahnke, Britta Stöckmann Kiel, Germany Uniwersytet im. Adama Mickiewicza w Poznaniu When it comes to games, dice belong to the oldest playthings or gambling instruments men have used to pass their time and/or make some money, and it is striking that still today it is hard to imagine the realm of board and table games1 without them. Dominions fell, Caesars were overthrown, however, the die is still rolling – but is it also still ruling? Trying to answer this question, we approach the topic from two angles, analysing !rst the historical and then the current situation. In the !rst part the authors would like to give a quick retrospection into the history of the die to highlight a few outstanding facts about dice and gambling in their sociocultural context. "e second part then will discuss the cur- rent situation on the German board game market from a more technical and functional point of view: how dice are being integrated into board and table games, and how the out- come is being received. To narrow down the !eld we will concentrate on this speci!c range and leave out dice in casino games as well as in RPGs. "e focus on German board games is due to the fact that they constitute one of the biggest board game markets worldwide and therefore provides a lot of material for the analysis, which at the same time does not exclude games from other countries. -

The Sphere Packing Problem in Dimension 8 Arxiv:1603.04246V2
The sphere packing problem in dimension 8 Maryna S. Viazovska April 5, 2017 8 In this paper we prove that no packing of unit balls in Euclidean space R has density greater than that of the E8-lattice packing. Keywords: Sphere packing, Modular forms, Fourier analysis AMS subject classification: 52C17, 11F03, 11F30 1 Introduction The sphere packing constant measures which portion of d-dimensional Euclidean space d can be covered by non-overlapping unit balls. More precisely, let R be the Euclidean d vector space equipped with distance k · k and Lebesgue measure Vol(·). For x 2 R and d r 2 R>0 we denote by Bd(x; r) the open ball in R with center x and radius r. Let d X ⊂ R be a discrete set of points such that kx − yk ≥ 2 for any distinct x; y 2 X. Then the union [ P = Bd(x; 1) x2X d is a sphere packing. If X is a lattice in R then we say that P is a lattice sphere packing. The finite density of a packing P is defined as Vol(P\ Bd(0; r)) ∆P (r) := ; r > 0: Vol(Bd(0; r)) We define the density of a packing P as the limit superior ∆P := lim sup ∆P (r): r!1 arXiv:1603.04246v2 [math.NT] 4 Apr 2017 The number be want to know is the supremum over all possible packing densities ∆d := sup ∆P ; d P⊂R sphere packing 1 called the sphere packing constant. For which dimensions do we know the exact value of ∆d? Trivially, in dimension 1 we have ∆1 = 1. -

Sphere Packing, Lattice Packing, and Related Problems
Sphere packing, lattice packing, and related problems Abhinav Kumar Stony Brook April 25, 2018 Sphere packings Definition n A sphere packing in R is a collection of spheres/balls of equal size which do not overlap (except for touching). The density of a sphere packing is the volume fraction of space occupied by the balls. ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ In dimension 1, we can achieve density 1 by laying intervals end to end. In dimension 2, the best possible is by using the hexagonal lattice. [Fejes T´oth1940] Sphere packing problem n Problem: Find a/the densest sphere packing(s) in R . In dimension 2, the best possible is by using the hexagonal lattice. [Fejes T´oth1940] Sphere packing problem n Problem: Find a/the densest sphere packing(s) in R . In dimension 1, we can achieve density 1 by laying intervals end to end. Sphere packing problem n Problem: Find a/the densest sphere packing(s) in R . In dimension 1, we can achieve density 1 by laying intervals end to end. In dimension 2, the best possible is by using the hexagonal lattice. [Fejes T´oth1940] Sphere packing problem II In dimension 3, the best possible way is to stack layers of the solution in 2 dimensions. This is Kepler's conjecture, now a theorem of Hales and collaborators. mmm m mmm m There are infinitely (in fact, uncountably) many ways of doing this! These are the Barlow packings. Face centered cubic packing Image: Greg A L (Wikipedia), CC BY-SA 3.0 license But (until very recently!) no proofs. In very high dimensions (say ≥ 1000) densest packings are likely to be close to disordered. -

Statistics and Probability Tetra Dice a Game Requires Each Player to Roll
High School – Statistics and Probability Tetra Dice A game requires each player to roll three specially shaped dice. Each die is a regular tetrahedron (four congruent, triangular faces). One face contains the number 1; one face contains the number 2; on another face appears the number 3; the remaining face shows the number 4. After a player rolls, the player records the numbers on the underneath sides of all three dice, and then calculates their sum. You win the game if the sum divides evenly by three. What is the probability of winning this game? Un juego exige que cada jugador lance tres dados con forma especial. Cada dado es un tetraedro regular (cuatro caras triangulares y congruentes). Una cara contiene el número 1; otra cara contiene el número 2; en otra cara aparece el número 3; la cara que sobra muestra el número 4. Después de que un jugador lanza los dados, el jugador registra los números de los lados cara abajo de los tres dados, y luego calcula su suma. Se gana el juego si la suma se divide exactamente por tres. ¿Cuál es la probabilidad de ganar este juego? В этой игре от каждого игрока требуется бросить три игральных кубика особенной формы. Каждый игральный кубик представляет собой правильный тетраэдр (четыре подобные треугольные грани). На однойграни стоит цифра 1; на одной грани стоит цифра 2; ещё на одной грани стоит цифра 3; на последней грани стоит цифра 4. После броска игрок записывает цифры, выпавшие на нижнейграни всех трёх кубиков, и затем вычисляет их сумму. Выигрывает тот игрок, чья сумма делится на три без остатка. -

Origins of Chess Protochess, 400 B.C
Origins of Chess Protochess, 400 B.C. to 400 A.D. by G. Ferlito and A. Sanvito FROM: The Pergamon Chess Monthly September 1990 Volume 55 No. 6 The game of chess, as we know it, emerged in the North West of ancient India around 600 A.D. (1) According to some scholars, the game of chess reached Persia at the time of King Khusrau Nushirwan (531/578 A.D.), though some others suggest a later date around the time of King Khusrau II Parwiz (590/628 A.D.) (2) Reading from the old texts written in Pahlavic, the game was originally known as "chatrang". With the invasion of Persia by the Arabs (634/651 A.D.), the game’s name became "shatranj" because the phonetic sounds of "ch" and "g" do not exist in Arabic language. The game spread towards the Mediterranean coast of Africa with the Islamic wave of military expansion and then crossed over to Europe. However, other alternative routes to some parts of Europe may have been used by other populations who were playing the game. At the moment, this "Indian, Persian, Islamic" theory on the origin of the game is accepted by the majority of scholars, though it is fair to mention here the work of J. Needham and others who suggested that the historical chess of seventh century India was descended from a divinatory game (or ritual) in China. (3) On chess theories, the most exhaustive account founded on deep learning and many years’ studies is the A History of Chess by the English scholar, H.J.R. -

Global Optimization Approach to Unequal Sphere Packing Problems in 3D1
JOURNAL OF OPTIMIZATION THEORY AND APPLICATIONS: Vol. 114, No. 3, pp. 671–694, September 2002 (2002) Global Optimization Approach to Unequal Sphere Packing Problems in 3D1 2 3 A. SUTOU AND Y. DAI Communicated by P. M. Pardalos Abstract. The problem of the unequal sphere packing in a 3-dimen- sional polytope is analyzed. Given a set of unequal spheres and a poly- tope, the double goal is to assemble the spheres in such a way that (i) they do not overlap with each other and (ii) the sum of the volumes of the spheres packed in the polytope is maximized. This optimization has an application in automated radiosurgical treatment planning and can be formulated as a nonconvex optimization problem with quadratic constraints and a linear objective function. On the basis of the special structures associated with this problem, we propose a variety of algorithms which improve markedly the existing simplicial branch-and- bound algorithm for the general nonconvex quadratic program. Further, heuristic algorithms are incorporated to strengthen the efficiency of the algorithm. The computational study demonstrates that the proposed algorithm can obtain successfully the optimization up to a limiting size. Key Words. Nonconvex quadratic programming, unequal sphere packing problem, simplicial branch-and-bound algorithm, LP relax- ation, heuristic algorithms. 1. Introduction The optimization of the packing of unequal spheres in a 3-dimensional polytope is analyzed. Given a set of unequal spheres and a polytope, the 1The authors thank two anonymous referees for their valuable comments. The work of the second author was partially supported by Grant-in-Aid C-13650444 from the Ministry of Education, Science, Sports, and Culture of Japan. -

Sphere Packing
Sphere packing Henry Cohn IAP Math Lecture Series January 16, 2015 The sphere packing problem How densely can we pack identical spheres into space? Not allowed to overlap (but can be tangent). Density = fraction of space filled by the spheres. Why should we care? The densest packing is pretty obvious. It's not difficult to stack cannonballs or oranges. It's profoundly difficult to prove (Hales 1998, 2014). But why should anyone but mathematicians care? One answer is that it's a toy model for: Granular materials. Packing more complicated shapes into containers. Sphere packing is a first step towards these more complex problems. Varying the dimension What if we didn't work in three-dimensional space? The two-dimensional analogue is packing circles in the plane. Still tricky to prove, but not nearly as difficult (Thue 1892). What about one dimension? What's a one-dimensional sphere? Spheres in different dimensions Sphere centered at x with radius r means the points at distance r from x. r x Ordinary sphere in three dimensions, circle in two dimensions. Just two points in one dimension: r x The inside of a one-dimensional sphere is an interval. r x One-dimensional sphere packing is boring: (density = 1) Two-dimensional sphere packing is prettier and more interesting: (density ≈ 0:91) Three dimensions strains human ability to prove: (density ≈ 0:74) What about four dimensions? Is that just crazy? Some history Thomas Harriot (1560{1621) Mathematical assistant to Sir Walter Raleigh. A Brief and True Report of the New Found Land of Virginia (1588) First to study the sphere packing problem. -

Tetrahedron Probability Lab Name______
Tetrahedron Probability Lab Name______________________ Follow the directions carefully and answer all questions. 1. You have two regular tetrahedron templates. LABEL the faces of one of the tetrahedrons with the words YELLOW, RED, BLUE, and GREEN. 2. Fold the tetrahedron to form a four-sided die. Tape the sides. Note that there are tabs on the template to help with the taping. 3. Roll this “die” 20 times. Record how many time each color lands face down by placing a tally mark in the correct space in the table below. YELLOW RED BLUE GREEN 4. On the basis of your 20 rolls, does it appear that one color is more likely to land face down? ________ If so, what color?_______________ 5. Based upon your 20 rolls, express the probability (with a denominator of 20) that the GREEN face will land face down?___________ The RED face? __________ The YELLOW face?___________ The BLUE face?____________ What should be the sum of these four fractions?______________ 6. Roll your tetrahedron die another 20 times. Keep a record similar to the record from questions 3. Record your results below. YELLOW RED BLUE GREEN 7. Did you get approximately the same results?__________________________ All Rights Reserved © MathBits.com 8. Now, combine the results of all 40 rolls of the tetrahedron die. Using a fraction whose denominator is 40, write the probability of each color landing face down on any given roll of the die. GREEN_______ RED_______ YELLOW _______ BLUE _______ 9. Was your rolling of this die a good, fair sampling? _____ Why, or why not? 10. -

BAR DICE in the SAN FRANCISCO BAY AREA Alan Dundes Department of Anthropology University of California Berkeley, California and Carl R
BAR DICE IN THE SAN FRANCISCO BAY AREA Alan Dundes Department of Anthropology University of California Berkeley, California and Carl R. Pagter normal price of the drink; if the bartender loses, INTRODUCTION the customer gets a free drink.) Of the more than Games involving the use of dice are among the 20 bar dice games reported here, Boss Dice-with oldest forms of organized human play. Dice games nothing wild-is by far the most common game be- have been widely reported from many different tween customer and bartender. cultural areas. In the United States, dice games are Bars which permit dice games normally have commonly associated with gambling, and in Neva- multiple sets of dice cups and dice, which are pro- da, where there is legalized gambling, one may find vided to partrons upon request. It is not uncom- a variety of such traditional games as craps. Dice mon for such bars to be sought out by devotees are not associated solely with professional gamblers of bar dice games. Even if these bars are not con- inasmuch as they are employed as an integral part sciously sought out, they may well have achieved of numerous children's board games, e.g., Par- the popularity they possess in part because of the cheesi, Monopoly, etc. ambiance of dice play. On the other hand, the One of the most flourishing groups of dice noise of numerous dice cups being banged down on games in contemporary America consists of those the bar does prove annoying to some customers. commonly played at bars. -
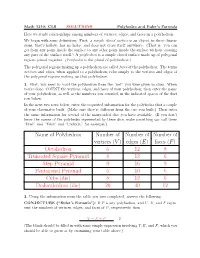
Edges (E) Faces (F) Octahedron 6 12 8 Truncated Square Pyramid 8
Math 1310: CLS SOLUTIONS Polyhedra and Euler's Formula Here we study relationships among numbers of vertices, edges, and faces in a polyhedron. We begin with some definitions. First: a simple closed surface is an object, in three dimen- sions, that's hollow, has no holes, and does not cross itself anywhere. (That is: you can get from any point inside the surface to any other point inside the surface without crossing any part of the surface itself.) A polyhedron is a simple closed surface made up of polygonal regions joined together. (Polyhedra is the plural of polyhedron.) The polygonal regions making up a polyhedron are called faces of the polyhedron. The terms vertices and edges, when applied to a polyhedron, refer simply to the vertices and edges of the polygonal regions making up that polyhedron. 1. First, you need to build the polyhedron from the \net" you were given in class. When you're done, COUNT the vertices, edges, and faces of your polyhedron; then enter the name of your polyhedron, as well as the numbers you counted, in the indicated spaces of the first row below. In the next two rows below, enter the requested information for the polyhedra that a couple of your classmates built. (Make sure they're different from the one you built.) Then enter the same information for several of the many-sided dice you have available. (If you don't know the names of the polyhedra represented by these dice, make something up: call them \Fred" and \Taku" and \Lucinda," for example.) Name of Polyhedron Number of Number of Number of vertices (V ) edges (E) faces (F ) Octahedron 6 12 8 Truncated Square Pyramid 8 12 6 Step Pyramid 9 16 9 Pentagonal Pyramid 6 10 6 Cube (die) 8 12 6 Dodecahedron (die) 20 30 12 2.