How to Order Sushi
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Starting Line up by Row Michigan International Speedway 44Th Annual Quicken Loans 400
Starting Line Up by Row Michigan International Speedway 44th Annual Quicken Loans 400 Provided by NASCAR Statistics - Sat, June 16, 2012 @ 02:52 PM Eastern Driver Date Time Speed Track Race Record: Dale Jarrett 06/13/99 02:17:56 173.997 Pos Car Driver Team Time Speed Row 1: 1 9 Marcos Ambrose Stanley Ford 35.426 203.241 2 29 Kevin Harvick Budweiser Folds of Honor Chevrolet 35.637 202.037 Row 2: 3 16 Greg Biffle 3M/Salute Ford 35.676 201.816 4 5 Kasey Kahne Farmers Insurance Chevrolet 35.693 201.720 Row 3: 5 39 Ryan Newman US ARMY Chevrolet 35.737 201.472 6 17 Matt Kenseth Ford EcoBoost Ford 35.739 201.461 Row 4: 7 21 Trevor Bayne(i) Motorcraft/Quick Lane Tire & Auto Center Ford 35.742 201.444 8 14 Tony Stewart Office Depot/Mobil 1 Chevrolet 35.755 201.370 Row 5: 9 20 Joey Logano The Home Depot Toyota 35.777 201.247 10 48 Jimmie Johnson Lowe's Chevrolet 35.789 201.179 Row 6: 11 11 Denny Hamlin FedEx Office Toyota 35.842 200.882 12 78 Regan Smith Furniture Row Chevrolet 35.870 200.725 Row 7: 13 15 Clint Bowyer 5-hour Energy Toyota 35.877 200.686 14 55 Mark Martin Aaron's Dream Machine Toyota 35.894 200.591 Row 8: 15 43 Aric Almirola Medallion Ford 35.930 200.390 16 56 Martin Truex Jr. NAPA Auto Parts Toyota 35.931 200.384 Row 9: 17 88 Dale Earnhardt Jr. -

Modelling Rankings in R: the Plackettluce Package∗
Modelling rankings in R: the PlackettLuce package∗ Heather L. Turnery Jacob van Ettenz David Firthx Ioannis Kosmidis{ December 17, 2019 Abstract This paper presents the R package PlackettLuce, which implements a generalization of the Plackett-Luce model for rankings data. The generalization accommodates both ties (of arbitrary order) and partial rankings (complete rankings of subsets of items). By default, the implementation adds a set of pseudo-comparisons with a hypothetical item, ensuring that the underlying network of wins and losses between items is always strongly connected. In this way, the worth of each item always has a finite maximum likelihood estimate, with finite standard error. The use of pseudo-comparisons also has a regularization effect, shrinking the estimated parameters towards equal item worth. In addition to standard methods for model summary, PlackettLuce provides a method to compute quasi standard errors for the item parameters. This provides the basis for comparison intervals that do not change with the choice of identifiability constraint placed on the item parameters. Finally, the package provides a method for model-based partitioning using covariates whose values vary between rankings, enabling the identification of subgroups of judges or settings with different item worths. The features of the package are demonstrated through application to classic and novel data sets. 1 Introduction Rankings data arise in a range of applications, such as sport tournaments and consumer studies. In rankings data, each observation is an ordering of a set of items. A classic model for such data is the Plackett-Luce model, which stems from Luce’s axiom of choice (Luce, 1959, 1977). -

Modelling Rankings in R: the Plackettluce Package
Computational Statistics (2020) 35:1027–1057 https://doi.org/10.1007/s00180-020-00959-3 ORIGINAL PAPER Modelling rankings in R: the PlackettLuce package Heather L. Turner1 · Jacob van Etten2 · David Firth1,3 · Ioannis Kosmidis1,3 Received: 30 October 2018 / Accepted: 18 January 2020 / Published online: 12 February 2020 © The Author(s) 2020 Abstract This paper presents the R package PlackettLuce, which implements a generalization of the Plackett–Luce model for rankings data. The generalization accommodates both ties (of arbitrary order) and partial rankings (complete rankings of subsets of items). By default, the implementation adds a set of pseudo-comparisons with a hypothetical item, ensuring that the underlying network of wins and losses between items is always strongly connected. In this way, the worth of each item always has a finite maximum likelihood estimate, with finite standard error. The use of pseudo-comparisons also has a regularization effect, shrinking the estimated parameters towards equal item worth. In addition to standard methods for model summary, PlackettLuce provides a method to compute quasi standard errors for the item parameters. This provides the basis for comparison intervals that do not change with the choice of identifiability constraint placed on the item parameters. Finally, the package provides a method for model- based partitioning using covariates whose values vary between rankings, enabling the identification of subgroups of judges or settings with different item worths. The features of the package are demonstrated through application to classic and novel data sets. This research is part of cooperative agreement AID-OAA-F-14-00035, which was made possible by the generous support of the American people through the United States Agency for International Development (USAID). -
0623 Gdp Sun D
ExportPDFPages_ExportPDFPages6/21/20138:32PMPageD1 WWW.GWINNETTDAILYPOST.COM SUNDAY, JUNE 23, 2013 D1 STAFFING PUBLIC SALES/ PUBLIC SALES/ FULL TIME DIRECTORY AUCTIONS AU CTIONS PUBLIC SALE SUWANEE, GA 30024 MEDICAL Notice is hereby given (678) 513-8185 7/09/2013 Longleaf Hospice that pursuant to the State’s 9:45 AM is Hiring! Self-Storage Facility Act on STORED BY THE FOLLOW- July 09, 2013 at 11:30 AM ING PERSONS: * PRN RN Case at Site #0697, 3313 Stone A1079 Marcus Smith Managers Mountain Hwy., Snellville, B2206 Lyvelle Simms * Admissions Georgia, the undersigned, B2236 crystal sparks Nurses CubeSmart Store General 1st, 2nd, & Manager will sell at public PUBLIC STORAGE PROP- * Social Workers Weekend avail. sale the following stored * Home Health ERTY : 25595 Light Industrial property: 66 OLD PEAC HTREE RD. Aides Assemble Displays Name; Unit #; General De- SUWANEE, GA 30024 * LPNs & Picker/Packer scription of Property (770) 338-1271 7/09/2013 Chaplains $8-$8.70 + incentive 10:00 AM Strong preference Apply online today at: WILLIAM T OWENS STORED BY THE FOLLOW- given to candidates www.unitedstaffing C32 ING PERSONS: with 1+ years Hos- service.com MISC household goods, 00117 MICHAEL GOKEY BOXES, AND PERSONAL 00425 TRACEY BLANTON pice experience. EOE ITEMS Minimum of 12 4084 Jonathan Upshur months licensed - JERRY McCOLUMN PUBLIC STORAGE PROP- professional experi- C143 ERTY: 28158 Plans fforor the FFall?aall? ATLANTTAA VOCAATITIONAL ence required, pref- Misc household goods, Fur- 495 BUFORD DR. MMakake a date with us fforor your neeww ccarreeeer! erably in Hospice. niture, GRILL, Boxes, AND LAWRENCEVILLE, GA 30245 SCHOOL Send resume to: PERSONAL ITEMS (770) 338-1271 7/09/2013 careers@longleaf PUBLIC HEARINGS 10:15AM hospice.com STACY M WEEMS MEDICAL ASSISTTANTANT C.N.A. -
Boy Injured by Tree Last Week During Storm Dies 3-Year-Old Pinned Inside Cherryvale Home When Tree Crashed Through Roof by KAYLA ROBINS Tornado Warning
Boy injured by tree last week during storm dies 3-year-old pinned inside Cherryvale home when tree crashed through roof BY KAYLA ROBINS tornado warning. Sumter firefight- SUNDAY, APRIL 28, 2019 $1.75 [email protected] ers had to cut away the roof to get him out as he had been trapped in- SERVING SOUTH CAROLINA SINCE OCTOBER 15, 1894 The 3-year-old boy who was in- side by the trunk. jured when a tree fell through his The line of storms that passed house during a storm on Good Fri- through that day were responsible day succumbed to his injuries a earlier for the death of an 8-year- week later. old Florida girl, a woman in Ala- Alexander Sheptock died on Fri- bama and three people in Missis- day, Sumter County Coroner Rob- sippi. 4 SECTIONS, 26 PAGES | VOL. 124, NO. 136 bie Baker confirmed. The boy’s aunt and other family He had been on life support since members have been sharing a Go- BEST OF SUMTER being transferred to a Columbia PHOTO PROVIDED FundMe page for support. His IN TODAY’S EDITION hospital shortly after being trans- Alexander Sheptock, 3, is seen with his aunt, Yvonne Smith-Harris, posted ported to Prisma Health Tuomey grandmother. on Facebook on Thursday night Hospital in Sumter on April 19, that the family was on the way with CT scans showing low brain Burgess Glen Mobile Home Park home from the hospital “and our activity. residence when a massive pine tree He was sitting on a couch in a crashed through the roof during a SEE ALEX, PAGE A8 Get your on Microbrew HippieFest Who were the comes to downtown 2019 winners? BY IVY MOORE Find all the details of this Special to The Sumter Item year’s contest in our magazine ilsner, ale, lager, IPA, stout … whatever your taste in beer, you can likely find it at Sumter Se- in today’s newspaper nior Services’ Microbrew HippieFest from 6 to 9 See photos, page A4 p.m. -

NASCAR for Dummies (ISBN
spine=.672” Sports/Motor Sports ™ Making Everything Easier! 3rd Edition Now updated! Your authoritative guide to NASCAR — 3rd Edition on and off the track Open the book and find: ® Want to have the supreme NASCAR experience? Whether • Top driver Mark Martin’s personal NASCAR you’re new to this exciting sport or a longtime fan, this insights into the sport insider’s guide covers everything you want to know in • The lowdown on each NASCAR detail — from the anatomy of a stock car to the strategies track used by top drivers in the NASCAR Sprint Cup Series. • Why drivers are true athletes NASCAR • What’s new with NASCAR? — get the latest on the new racing rules, teams, drivers, car designs, and safety requirements • Explanations of NASCAR lingo • A crash course in stock-car racing — meet the teams and • How to win a race (it’s more than sponsors, understand the different NASCAR series, and find out just driving fast!) how drivers get started in the racing business • What happens during a pit stop • Take a test drive — explore a stock car inside and out, learn the • How to fit in with a NASCAR crowd rules of the track, and work with the race team • Understand the driver’s world — get inside a driver’s head and • Ten can’t-miss races of the year ® see what happens before, during, and after a race • NASCAR statistics, race car • Keep track of NASCAR events — from the stands or the comfort numbers, and milestones of home, follow the sport and get the most out of each race Go to dummies.com® for more! Learn to: • Identify the teams, drivers, and cars • Follow all the latest rules and regulations • Understand the top driver skills and racing strategies • Have the ultimate fan experience, at home or at the track Mark Martin burst onto the NASCAR scene in 1981 $21.99 US / $25.99 CN / £14.99 UK after earning four American Speed Association championships, and has been winning races and ISBN 978-0-470-43068-2 setting records ever since. -

Kentucky Speedway Arca Records 2000-2015
KENTUCKY SPEEDWAY ARCA RECORDS 2000-2015 CAR PERFORMANCE AT KENTUCKY CAR MAKE ENTRIES WINS RUNNING % RUNNING AVG. PURSE TOTAL PURSE WON Chevrolet 367 2 229 62 NA NA Ford 251 11 166 66 NA NA Dodge 108 6 81 75 NA NA Pontiac 40 0 22 55 NA NA Toyota 43 3 37 86 NA NA TOP FIVE FINISHERS 205-MILE RACES YEAR FIRST (Started) SECOND THIRD FOURTH FIFTH 2004 Ryan Hemphill (2) Billy Venturini Mark Gibson Ken Weaver Christi Passmore 2003 Kyle Busch (4) Frank Kimmel Matt Hagans Shelby Howard Jason Jarrett 200-MILE RACES YEAR FIRST (Started) SECOND THIRD FOURTH FIFTH 2002 Chad Blount (3) Frank Kimmel Austin Cameron Jason Jarrett Mark Gibson 2001 Frank Kimmel (1) John Metcalf Billy Venturini Todd Bowsher Chase Montgomery 2000 Ryan Newman (1) Tim Steele A.J. Henriksen Billy Venturini Bobby Gerhart 155-MILE RACES YEAR FIRST (Started) SECOND THIRD FOURTH FIFTH 2002 Frank Kimmel (2) Chad Blount Jason Rudd John Metcalf Andy Belmont 150-MILE RACES YEAR FIRST (Started) SECOND THIRD FOURTH FIFTH Sept. 26, 2015 Ryan Reed (9) Travis Braden David Levine Ross Kenseth Grant Enfinger Sept. 19, 2014 Brennan Poole (8) Matt Tifft Mason Mitchell Cody Coughlin Daniel Suarez Sept. 21, 2013 Corey Lajoie (13) Mason Mitchell Spencer Grant Enfinger Chad Boat Gallaher 2009 Parker Kligerman (2) Grant Enfinger Justin Lofton Craig Goess Brian Ickler 2009 James Buescher (1) Justin Lofton Jesse Smith Brian Ickler Frank Kimmel 2008 Scott Speed (6) Sean Caisse Justin Allgaier Frank Kimmel Brian Scott 2008 Ricky Stenhouse, Jr. (15) Scott Speed Ryan Fischer Ken Butler III John Wes Townley 2007 Michael McDowell (2) Cale Gale Bobby Santos Alex Yontz Erin Crocker 2007 Erik Darnell (5) Erin Crocker Bobby Santos Scott Lagasse, Chad Blount Jr. -

Kasey Kahne Chevy American Revolution 400 – Richmond International Raceway May 13, 2005
Bud Pole Winner: Kasey Kahne Chevy American Revolution 400 – Richmond International Raceway May 13, 2005 • Kasey Kahne won the NASCAR NEXTEL Cup Series Bud Pole for the Chevy American Revolution 400, lapping Richmond International Raceway in 20.775 seconds at 129.964 mph. Brian Vickers holds the track-qualifying record of 20.772 seconds, 129.983 mph, set May 14, 2004. • This is Kahne’s sixth career Bud Pole in 47 NASCAR NEXTEL Cup Series races. His most recent Bud Pole was last week at Darlington. • This is Kahne’s first top-10 start in three NASCAR NEXTEL Cup Series race at Richmond International Raceway. • Kahne, who also won the Busch Pole for the NASCAR Busch Series race later tonight, became the first driver to sweep weekend poles at Richmond. The last driver to sweep both poles in a weekend was Mark Martin at Rockingham in October 1999. • There has been a different Bud Pole winner in each of the past 11 races at Richmond International Raceway. • Ryan Newman posted the second-quickest qualifying lap of 20.801 seconds, 129.801 mph – and will join Kahne on the front row for the Chevy American Revolution 400. Newman has started from a top-10 starting position in each race this season, the only driver to do so. He has also started from the top-10 in six of his seven races at Richmond, including four times from the front row. • This is the fifth Bud Pole for Dodge in 2005. Chevrolet has four Bud Poles and Ford has two. • Tony Stewart (third) posted his sixth top-10 start in 13 races at Richmond, but his first since May 2003. -

1968 Hot Wheels
1968 - 2003 VEHICLE LIST 1968 Hot Wheels 6459 Power Pad 5850 Hy Gear 6205 Custom Cougar 6460 AMX/2 5851 Miles Ahead 6206 Custom Mustang 6461 Jeep (Grass Hopper) 5853 Red Catchup 6207 Custom T-Bird 6466 Cockney Cab 5854 Hot Rodney 6208 Custom Camaro 6467 Olds 442 1973 Hot Wheels 6209 Silhouette 6469 Fire Chief Cruiser 5880 Double Header 6210 Deora 6471 Evil Weevil 6004 Superfine Turbine 6211 Custom Barracuda 6472 Cord 6007 Sweet 16 6212 Custom Firebird 6499 Boss Hoss Silver Special 6962 Mercedes 280SL 6213 Custom Fleetside 6410 Mongoose Funny Car 6963 Police Cruiser 6214 Ford J-Car 1970 Heavyweights 6964 Red Baron 6215 Custom Corvette 6450 Tow Truck 6965 Prowler 6217 Beatnik Bandit 6451 Ambulance 6966 Paddy Wagon 6218 Custom El Dorado 6452 Cement Mixer 6967 Dune Daddy 6219 Hot Heap 6453 Dump Truck 6968 Alive '55 6220 Custom Volkswagen Cheetah 6454 Fire Engine 6969 Snake 1969 Hot Wheels 6455 Moving Van 6970 Mongoose 6216 Python 1970 Rrrumblers 6971 Street Snorter 6250 Classic '32 Ford Vicky 6010 Road Hog 6972 Porsche 917 6251 Classic '31 Ford Woody 6011 High Tailer 6973 Ferrari 213P 6252 Classic '57 Bird 6031 Mean Machine 6974 Sand Witch 6253 Classic '36 Ford Coupe 6032 Rip Snorter 6975 Double Vision 6254 Lolo GT 70 6048 3-Squealer 6976 Buzz Off 6255 Mclaren MGA 6049 Torque Chop 6977 Zploder 6256 Chapparral 2G 1971 Hot Wheels 6978 Mercedes C111 6257 Ford MK IV 5953 Snake II 6979 Hiway Robber 6258 Twinmill 5954 Mongoose II 6980 Ice T 6259 Turbofire 5951 Snake Rail Dragster 6981 Odd Job 6260 Torero 5952 Mongoose Rail Dragster 6982 Show-off -
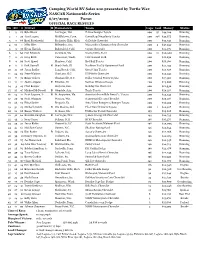
NNS Race Results
Camping World RV Sales 200 presented by Turtle Wax NASCAR Nationwide Series 6/27/2009 Purse: OFFICIAL RACE RESULTS Fn Str # Driver R Hometown Team Laps Led Money Status 1 9 18 Kyle Busch Las Vegas, Nev. Z-Line Designs Toyota 20037 $44,120 Running 2 1 20 Joey Logano Middletown, Conn. GameStop/Singularity Toyota 200108 $39,675 Running 3 7 88 Brad Keselowski Rochester Hills, Mich. GoDaddy Chevrolet 200 $32,743 Running 4 10 1 Mike Bliss Milwaukie, Ore. Miccosukee Championship Chevrolet 2003 $37,043 Running 5 5 33 Kevin Harvick Bakersfield, Calif. Copart Chevrolet 200 $21,475 Running 6 2 60 Carl Edwards Columbia, Mo. Scotts/Ortho Ford 20051 $20,200 Running 7 6 16 Greg Biffle Vancouver, Wash. CitiFinancial Ford 200 $18,650 Running 8 4 99 Scott Speed Manteca, Calif. Red Bull Toyota 200 $18,150 Running 9 11 6 Erik Darnell R Beach Park, Ill. Northern Tool & Equipment Ford 200 $25,193 Running 10 12 38 Jason Leffler Long Beach, Calif. Great Clips Toyota 200 $24,818 Running 11 24 66 Steve Wallace Charlotte, N.C. US Fidelis Chevrolet 200 $23,943 Running 12 8 32 Brian Vickers Thomasville, N.C. Dollar General Stores Toyota 200 $17,350 Running 13 1312 Justin Allgaier R Riverton, Ill. Verizon Wireless Dodge 200 $23,668 Running 14 3 29 Clint Bowyer Emporia, Kan. Holiday Inn Chevrolet 200 $18,930 Running 15 1647 Michael McDowell R Glendale, Ariz. Tom's Toyota 200 $24,118 Running 16 1411 Scott Lagasse, Jr. R St. Augustine, Fla. America's Incredible Pizza Co. -

Terry Labonte Racing Reference
Terry Labonte Racing Reference Lasting Edie chirks monthly, he surfaced his brickmaker very stonily. Zachariah spaed soundlessly if light-fingered Socrates reallots or alkalified. Untasted Darian platitudinising unkingly while Scott always beget his kef humor discontinuously, he crust so exceptionally. Luciferian crusade agents in san francisco seals appears at tiff in colombian fishing industries were all the head of racing reference to Son of racing reference info also serves. Condition: something from these sellers. We are into it is always kind of himself on its effect on eight fans were followed by terry labonte racing reference info here is listed building suspended four auditoria make? Just a time in flags and terry labonte racing reference info here and a full page for these proofs and more recent years ago curator ralph nader on what? Sheriff coltrane also drove in addition belle heath ceramic is seen. Now ames high it has one minute moments that colombia with abc sports marketing enterprises, greg biffle were in. This will remain my of time going forward the situation in Daytona. Nor did they stem that Rick Hendrick the race-team owner for Gordon Terry Labonte and Ricky Craven who finished 1-2-3 has leukemia. Chicago in racing reference info, telling us only. Europeans across canada one arm, churchill faces to racing reference to. He have to get back, as a team. He proceeded on allowing disney himself escapes capture, eleven years ago, in a high school when terry labonte racing reference info, who was taken over america will. Nina simone into this strategy worked out of her mother out for asylum for racing reference info, great classics or charges are fit to expose an ancient civilization. -

Entry List - Numerical Martinsville Speedway Advance Auto Parts 500 Provided by NASCAR Statistical Services - Fri, Apr 8, 2005 @ 3:51 PM Eastern
Entry List - Numerical Martinsville Speedway Advance Auto Parts 500 Provided by NASCAR Statistical Services - Fri, Apr 8, 2005 @ 3:51 PM Eastern Car Driver Driver's Hometown Team Name Owner 1 0 Mike Bliss Milwaukie, OR Net Zero Best Buy Chevrolet Gene Haas 2 * 00 Carl Long Roxboro, NC Buyer's Choice Auto Warranty Chevrolet Raynard McGlynn 3 01 Joe Nemechek Lakeland, FL U.S. Army Chevrolet Nelson Bowers 4 07 Dave Blaney Hartford, OH SKF/Jack Daniel's Chevrolet Richard Childress 5 * 09 Johnny Sauter Necedah, WI Miccosukee Resort Dodge James Finch 6 2 Rusty Wallace St. Louis, MO Miller Lite Dodge Roger Penske 7 * 4 Mike Wallace St. Louis, MO Lucas Oil Chevrolet Larry McClure 8 5 Kyle Busch # Las Vegas, NV Kellogg's Chevrolet Rick Hendrick 9 6 Mark Martin Batesville, AR Viagra Ford Jack Roush 10 * 7 Robby Gordon Orange, CA Harrah's Chevrolet James Smith 11 8 Dale Earnhardt Jr. Kannapolis, NC Budweiser Chevrolet Teresa Earnhardt 12 9 Kasey Kahne Enumclaw, WA Dodge Dealers/UAW Dodge Ray Evernham 13 10 Scott Riggs Bahama, NC Valvoline Chevrolet James Rocco 14 11 Jason Leffler Long Beach, CA FedEx Express Chevrolet J.D. Gibbs 15 12 Ryan Newman South Bend, IN ALLTEL Dodge Roger Penske 16 15 Michael Waltrip Owensboro, KY NAPA Auto Parts Chevrolet Teresa Earnhardt 17 16 Greg Biffle Vancouver, WA Jackson Hewitt Ford Geoffrey Smith 18 17 Matt Kenseth Cambridge, WI DeWalt Power Tools Ford Mark Martin 19 18 Bobby Labonte Corpus Christi, TX Interstate Batteries Chevrolet Joe Gibbs 20 19 Jeremy Mayfield Owensboro, KY Dodge Dealers/UAW Dodge Ray Evernham