1 Simply-Typed Lambda Calculus
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Lecture Notes on the Lambda Calculus 2.4 Introduction to Β-Reduction
2.2 Free and bound variables, α-equivalence. 8 2.3 Substitution ............................. 10 Lecture Notes on the Lambda Calculus 2.4 Introduction to β-reduction..................... 12 2.5 Formal definitions of β-reduction and β-equivalence . 13 Peter Selinger 3 Programming in the untyped lambda calculus 14 3.1 Booleans .............................. 14 Department of Mathematics and Statistics 3.2 Naturalnumbers........................... 15 Dalhousie University, Halifax, Canada 3.3 Fixedpointsandrecursivefunctions . 17 3.4 Other data types: pairs, tuples, lists, trees, etc. ....... 20 Abstract This is a set of lecture notes that developed out of courses on the lambda 4 The Church-Rosser Theorem 22 calculus that I taught at the University of Ottawa in 2001 and at Dalhousie 4.1 Extensionality, η-equivalence, and η-reduction. 22 University in 2007 and 2013. Topics covered in these notes include the un- typed lambda calculus, the Church-Rosser theorem, combinatory algebras, 4.2 Statement of the Church-Rosser Theorem, and some consequences 23 the simply-typed lambda calculus, the Curry-Howard isomorphism, weak 4.3 Preliminary remarks on the proof of the Church-Rosser Theorem . 25 and strong normalization, polymorphism, type inference, denotational se- mantics, complete partial orders, and the language PCF. 4.4 ProofoftheChurch-RosserTheorem. 27 4.5 Exercises .............................. 32 Contents 5 Combinatory algebras 34 5.1 Applicativestructures. 34 1 Introduction 1 5.2 Combinatorycompleteness . 35 1.1 Extensionalvs. intensionalviewoffunctions . ... 1 5.3 Combinatoryalgebras. 37 1.2 Thelambdacalculus ........................ 2 5.4 The failure of soundnessforcombinatoryalgebras . .... 38 1.3 Untypedvs.typedlambda-calculi . 3 5.5 Lambdaalgebras .......................... 40 1.4 Lambdacalculusandcomputability . 4 5.6 Extensionalcombinatoryalgebras . 44 1.5 Connectionstocomputerscience . -

Lecture Notes on Types for Part II of the Computer Science Tripos
Q Lecture Notes on Types for Part II of the Computer Science Tripos Prof. Andrew M. Pitts University of Cambridge Computer Laboratory c 2016 A. M. Pitts Contents Learning Guide i 1 Introduction 1 2 ML Polymorphism 6 2.1 Mini-ML type system . 6 2.2 Examples of type inference, by hand . 14 2.3 Principal type schemes . 16 2.4 A type inference algorithm . 18 3 Polymorphic Reference Types 25 3.1 The problem . 25 3.2 Restoring type soundness . 30 4 Polymorphic Lambda Calculus 33 4.1 From type schemes to polymorphic types . 33 4.2 The Polymorphic Lambda Calculus (PLC) type system . 37 4.3 PLC type inference . 42 4.4 Datatypes in PLC . 43 4.5 Existential types . 50 5 Dependent Types 53 5.1 Dependent functions . 53 5.2 Pure Type Systems . 57 5.3 System Fw .............................................. 63 6 Propositions as Types 67 6.1 Intuitionistic logics . 67 6.2 Curry-Howard correspondence . 69 6.3 Calculus of Constructions, lC ................................... 73 6.4 Inductive types . 76 7 Further Topics 81 References 84 Learning Guide These notes and slides are designed to accompany 12 lectures on type systems for Part II of the Cambridge University Computer Science Tripos. The course builds on the techniques intro- duced in the Part IB course on Semantics of Programming Languages for specifying type systems for programming languages and reasoning about their properties. The emphasis here is on type systems for functional languages and their connection to constructive logic. We pay par- ticular attention to the notion of parametric polymorphism (also known as generics), both because it has proven useful in practice and because its theory is quite subtle. -

Open C++ Tutorial∗
Open C++ Tutorial∗ Shigeru Chiba Institute of Information Science and Electronics University of Tsukuba [email protected] Copyright c 1998 by Shigeru Chiba. All Rights Reserved. 1 Introduction OpenC++ is an extensible language based on C++. The extended features of OpenC++ are specified by a meta-level program given at compile time. For dis- tinction, regular programs written in OpenC++ are called base-level programs. If no meta-level program is given, OpenC++ is identical to regular C++. The meta-level program extends OpenC++ through the interface called the OpenC++ MOP. The OpenC++ compiler consists of three stages: preprocessor, source-to-source translator from OpenC++ to C++, and the back-end C++ com- piler. The OpenC++ MOP is an interface to control the translator at the second stage. It allows to specify how an extended feature of OpenC++ is translated into regular C++ code. An extended feature of OpenC++ is supplied as an add-on software for the compiler. The add-on software consists of not only the meta-level program but also runtime support code. The runtime support code provides classes and functions used by the base-level program translated into C++. The base-level program in OpenC++ is first translated into C++ according to the meta-level program. Then it is linked with the runtime support code to be executable code. This flow is illustrated by Figure 1. The meta-level program is also written in OpenC++ since OpenC++ is a self- reflective language. It defines new metaobjects to control source-to-source transla- tion. The metaobjects are the meta-level representation of the base-level program and they perform the translation. -

Let's Get Functional
5 LET’S GET FUNCTIONAL I’ve mentioned several times that F# is a functional language, but as you’ve learned from previous chapters you can build rich applications in F# without using any functional techniques. Does that mean that F# isn’t really a functional language? No. F# is a general-purpose, multi paradigm language that allows you to program in the style most suited to your task. It is considered a functional-first lan- guage, meaning that its constructs encourage a functional style. In other words, when developing in F# you should favor functional approaches whenever possible and switch to other styles as appropriate. In this chapter, we’ll see what functional programming really is and how functions in F# differ from those in other languages. Once we’ve estab- lished that foundation, we’ll explore several data types commonly used with functional programming and take a brief side trip into lazy evaluation. The Book of F# © 2014 by Dave Fancher What Is Functional Programming? Functional programming takes a fundamentally different approach toward developing software than object-oriented programming. While object-oriented programming is primarily concerned with managing an ever-changing system state, functional programming emphasizes immutability and the application of deterministic functions. This difference drastically changes the way you build software, because in object-oriented programming you’re mostly concerned with defining classes (or structs), whereas in functional programming your focus is on defining functions with particular emphasis on their input and output. F# is an impure functional language where data is immutable by default, though you can still define mutable data or cause other side effects in your functions. -

Category Theory and Lambda Calculus
Category Theory and Lambda Calculus Mario Román García Trabajo Fin de Grado Doble Grado en Ingeniería Informática y Matemáticas Tutores Pedro A. García-Sánchez Manuel Bullejos Lorenzo Facultad de Ciencias E.T.S. Ingenierías Informática y de Telecomunicación Granada, a 18 de junio de 2018 Contents 1 Lambda calculus 13 1.1 Untyped λ-calculus . 13 1.1.1 Untyped λ-calculus . 14 1.1.2 Free and bound variables, substitution . 14 1.1.3 Alpha equivalence . 16 1.1.4 Beta reduction . 16 1.1.5 Eta reduction . 17 1.1.6 Confluence . 17 1.1.7 The Church-Rosser theorem . 18 1.1.8 Normalization . 20 1.1.9 Standardization and evaluation strategies . 21 1.1.10 SKI combinators . 22 1.1.11 Turing completeness . 24 1.2 Simply typed λ-calculus . 24 1.2.1 Simple types . 25 1.2.2 Typing rules for simply typed λ-calculus . 25 1.2.3 Curry-style types . 26 1.2.4 Unification and type inference . 27 1.2.5 Subject reduction and normalization . 29 1.3 The Curry-Howard correspondence . 31 1.3.1 Extending the simply typed λ-calculus . 31 1.3.2 Natural deduction . 32 1.3.3 Propositions as types . 34 1.4 Other type systems . 35 1.4.1 λ-cube..................................... 35 2 Mikrokosmos 38 2.1 Implementation of λ-expressions . 38 2.1.1 The Haskell programming language . 38 2.1.2 De Bruijn indexes . 40 2.1.3 Substitution . 41 2.1.4 De Bruijn-terms and λ-terms . 42 2.1.5 Evaluation . -

Run-Time Type Information and Incremental Loading in C++
Run-time Type Information and Incremental Loading in C++ Murali Vemulapati Sriram Duvvuru Amar Gupta WP #3772 September 1993 PROFIT #93-11 Productivity From Information Technology "PROFIT" Research Initiative Sloan School of Management Massachusetts Institute of Technology Cambridge, MA 02139 USA (617)253-8584 Fax: (617)258-7579 Copyright Massachusetts Institute of Technology 1993. The research described herein has been supported (in whole or in part) by the Productivity From Information Technology (PROFIT) Research Initiative at MIT. This copy is for the exclusive use of PROFIT sponsor firms. Productivity From Information Technology (PROFIT) The Productivity From Information Technology (PROFIT) Initiative was established on October 23, 1992 by MIT President Charles Vest and Provost Mark Wrighton "to study the use of information technology in both the private and public sectors and to enhance productivity in areas ranging from finance to transportation, and from manufacturing to telecommunications." At the time of its inception, PROFIT took over the Composite Information Systems Laboratory and Handwritten Character Recognition Laboratory. These two laboratories are now involved in research re- lated to context mediation and imaging respectively. LABORATORY FOR ELEC RONICS A CENTERCFORENTER COORDINATION LABORATORY ) INFORMATION S RESEARCH RESE CH E53-310, MITAL"Room Cambridge, MA 02M142-1247 Tel: (617) 253-8584 E-Mail: [email protected] Run-time Type Information and Incremental Loading in C++ September 13, 1993 Abstract We present the design and implementation strategy for an integrated programming environment which facilitates specification, implementation and execution of persistent C++ programs. Our system is implemented in E, a persistent programming language based on C++. The environment provides type identity and type persistence, i.e., each user-defined class has a unique identity and persistence across compilations. -

Kodak Color Control Patches Kodak Gray
Kodak Color Control Patches 0 - - _,...,...,. Blue Green Yellow Red White 3/Color . Black Kodak Gray Scale A 1 2 a 4 s -- - --- - -- - -- - -- -- - A Study of Compile-time Metaobject Protocol :J/1\'-(Jt.-S~..)(:$/;:t::;i':_;·I'i f-.· 7 •[:]f-. :::JJl. (:~9 ~~Jf'?E By Shigeru Chiba chiba~is.s.u-tokyo.ac.jp November 1996 A Dissertation Submitted to Department of Information Science Graduate School of Science The Un iversity of Tokyo In Partial Fulfillment of the Requirements For the Degree of Doctor of Science. Copyright @1996 by Shigeru Chiba. All Rights Reserved. - - - ---- - ~-- -- -~ - - - ii A Metaobject Protocol for Enabling Better C++ Libraries Shigeru Chiba Department of Information Science The University of Tokyo chiba~is.s.u-tokyo.ac.jp Copyrighl @ 1996 by Shi geru Chiba. All Ri ghts Reserved. iii iv Abstract C++ cannot be used to implement control/data abstractions as a library if their implementations require specialized code for each user code. This problem limits programmers to write libraries in two ways: it makes some kinds of useful abstractions that inherently require such facilities impossi ble to implement, and it makes other abstractions difficult to implement efficiently. T he OpenC++ MOP addresses this problem by providing li braries the ability to pre-process a program in a context-sensitive and non-local way. That is, libraries can instantiate specialized code depending on how the library is used and, if needed, substitute it for the original user code. The basic protocol structure of the Open C++ MOP is based on that of the CLOS MOP, but the Open C++ MOP runs metaobjects only at compile time. -

Lambda-Calculus Types and Models
Jean-Louis Krivine LAMBDA-CALCULUS TYPES AND MODELS Translated from french by René Cori To my daughter Contents Introduction5 1 Substitution and beta-conversion7 Simple substitution ..............................8 Alpha-equivalence and substitution ..................... 12 Beta-conversion ................................ 18 Eta-conversion ................................. 24 2 Representation of recursive functions 29 Head normal forms .............................. 29 Representable functions ............................ 31 Fixed point combinators ........................... 34 The second fixed point theorem ....................... 37 3 Intersection type systems 41 System D ................................... 41 System D .................................... 50 Typings for normal terms ........................... 54 4 Normalization and standardization 61 Typings for normalizable terms ........................ 61 Strong normalization ............................. 68 ¯I-reduction ................................. 70 The ¸I-calculus ................................ 72 ¯´-reduction ................................. 74 The finite developments theorem ....................... 77 The standardization theorem ......................... 81 5 The Böhm theorem 87 3 4 CONTENTS 6 Combinatory logic 95 Combinatory algebras ............................. 95 Extensionality axioms ............................. 98 Curry’s equations ............................... 101 Translation of ¸-calculus ........................... 105 7 Models of lambda-calculus 111 Functional -

The Lambda Calculus Bharat Jayaraman Department of Computer Science and Engineering University at Buffalo (SUNY) January 2010
The Lambda Calculus Bharat Jayaraman Department of Computer Science and Engineering University at Buffalo (SUNY) January 2010 The lambda-calculus is of fundamental importance in the study of programming languages. It was founded by Alonzo Church in the 1930s well before programming languages or even electronic computers were invented. Church's thesis is that the computable functions are precisely those that are definable in the lambda-calculus. This is quite amazing, since the entire syntax of the lambda-calculus can be defined in just one line: T ::= V j λV:T j (TT ) The syntactic category T defines the set of well-formed expressions of the lambda-calculus, also referred to as lambda-terms. The syntactic category V stands for a variable; λV:T is called an abstraction, and (TT ) is called an application. We will examine these terms in more detail a little later, but, at the outset, it is remarkable that the lambda-calculus is capable of defining recursive functions even though there is no provision for writing recursive definitions. Indeed, there is no provision for writing named procedures or functions as we know them in conventional languages. Also absent are other familiar programming constructs such as control and data structures. We will therefore examine how the lambda-calculus can encode such constructs, and thereby gain some insight into the power of this little language. In the field of programming languages, John McCarthy was probably the first to rec- ognize the importance of the lambda-calculus, which inspired him in the 1950s to develop the Lisp programming language. -

Query Rewriting Using Views in a Typed Mediator
Язык СИНТЕЗ как ядро канонической информационной модели Л. А. Калиниченко ([email protected]) C. А. Ступников ([email protected]) Lecture outline Objectives of the language Frame language: semi-structured capabilities Type system of SYNTHESIS Classes and metaclasses Assertions Processes, workflows Formulae facilities of the language 2 History of the language . Preliminary draft version published in 1991 . First version published in 1993 . English version prepared in 1995 and extended in 1997 . Current version in English published in 2007 3 The SYNTHESIS is a multipurpose language The language is oriented on the following basic kinds of application: . serving as a kernel of the canonical information model; . providing facilities for unifying representation of heterogeneous information models of different kinds (of data, services, processes, ontologies); . providing sufficient modeling facilities for formalized definitions of mediators for various subject domains; . supporting mediation-based design of information systems; . providing modeling facilities for mediator and resource specifications for the mediation architecture; . serving for semantic reconciliation of the mediator and resource specifications to form compositions of resources refining mediator specifications; . serving as an interface for users during problem formulation and solving in various applications 4 Mediation orientation . Two different approaches to the problem of integrated representation of multiple information resources for an IS are distinguished: 1. moving from resources to problems (resource driven approach) 2. moving from an application to resources (application driven approach) The SYNTHESIS language is oriented on support of application-driven approach for mediation-based IS development. The mediator's layer is introduced to provide the users with the metainformation uniformly characterizing subject definitions in the canonical information model – providing application domain conceptual schema . -
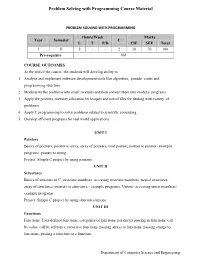
Problem Solving with Programming Course Material
Problem Solving with Programming Course Material PROBLEM SOLVING WITH PROGRAMMING Hours/Week Marks Year Semester C L T P/D CIE SEE Total I II 2 - - 2 30 70 100 Pre-requisite Nil COURSE OUTCOMES At the end of the course, the students will develop ability to 1. Analyze and implement software development tools like algorithm, pseudo codes and programming structure. 2. Modularize the problems into small modules and then convert them into modular programs 3. Apply the pointers, memory allocation techniques and use of files for dealing with variety of problems. 4. Apply C programming to solve problems related to scientific computing. 5. Develop efficient programs for real world applications. UNIT I Pointers Basics of pointers, pointer to array, array of pointers, void pointer, pointer to pointer- example programs, pointer to string. Project: Simple C project by using pointers. UNIT II Structures Basics of structure in C, structure members, accessing structure members, nested structures, array of structures, pointers to structures - example programs, Unions- accessing union members- example programs. Project: Simple C project by using structures/unions. UNIT III Functions Functions: User-defined functions, categories of functions, parameter passing in functions: call by value, call by reference, recursive functions. passing arrays to functions, passing strings to functions, passing a structure to a function. Department of Computer Science and Engineering Problem Solving with Programming Course Material Project: Simple C project by using functions. UNIT IV File Management Data Files, opening and closing a data file, creating a data file, processing a data file, unformatted data files. Project: Simple C project by using files. -

Brief Notes on the Category Theoretic Semantics of Simply Typed Lambda Calculus
University of Cambridge 2017 MPhil ACS / CST Part III Category Theory and Logic (L108) Brief Notes on the Category Theoretic Semantics of Simply Typed Lambda Calculus Andrew Pitts Notation: comma-separated snoc lists When presenting logical systems and type theories, it is common to write finite lists of things using a comma to indicate the cons-operation and with the head of the list at the right. With this convention there is no common notation for the empty list; we will use the symbol “”. Thus ML-style list notation nil a :: nil b :: a :: nil etc becomes , a , a, b etc For non-empty lists, it is very common to leave the initial part “,” of the above notation implicit, for example just writing a, b instead of , a, b. Write X∗ for the set of such finite lists with elements from the set X. 1 Syntax of the simply typed l-calculus Fix a countably infinite set V whose elements are called variables and are typically written x, y, z,... The simple types (with product types) A over a set Gnd of ground types are given by the following grammar, where G ranges over Gnd: A ::= G j unit j A x A j A -> A Write ST(Gnd) for the set of simple types over Gnd. The syntax trees t of the simply typed l-calculus (STLC) over Gnd with constants drawn from a set Con are given by the following grammar, where c ranges over Con, x over V and A over ST(Gnd): t ::= c j x j () j (t , t) j fst t j snd t j lx : A.