Chapter 6: Curve Fitting
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Unsupervised Contour Representation and Estimation Using B-Splines and a Minimum Description Length Criterion Mário A
IEEE TRANSACTIONS ON IMAGE PROCESSING, VOL. 9, NO. 6, JUNE 2000 1075 Unsupervised Contour Representation and Estimation Using B-Splines and a Minimum Description Length Criterion Mário A. T. Figueiredo, Member, IEEE, José M. N. Leitão, Member, IEEE, and Anil K. Jain, Fellow, IEEE Abstract—This paper describes a new approach to adaptive having external/potential energy, which is a func- estimation of parametric deformable contours based on B-spline tion of certain features of the image The equilibrium (min- representations. The problem is formulated in a statistical imal total energy) configuration framework with the likelihood function being derived from a re- gion-based image model. The parameters of the image model, the (1) contour parameters, and the B-spline parameterization order (i.e., the number of control points) are all considered unknown. The is a compromise between smoothness (enforced by the elastic parameterization order is estimated via a minimum description nature of the model) and proximity to the desired image features length (MDL) type criterion. A deterministic iterative algorithm is (by action of the external potential). developed to implement the derived contour estimation criterion. Several drawbacks of conventional snakes, such as their “my- The result is an unsupervised parametric deformable contour: it adapts its degree of smoothness/complexity (number of control opia” (i.e., use of image data strictly along the boundary), have points) and it also estimates the observation (image) model stimulated a great amount of research; although most limitations parameters. The experiments reported in the paper, performed of the original formulation have been successfully addressed on synthetic and real (medical) images, confirm the adequacy and (see, e.g., [6], [9], [10], [34], [38], [43], [49], and [52]), non- good performance of the approach. -

Chapter 26: Mathcad-Data Analysis Functions
Lecture 3 MATHCAD-DATA ANALYSIS FUNCTIONS Objectives Graphs in MathCAD Built-in Functions for basic calculations: Square roots, Systems of linear equations Interpolation on data sets Linear regression Symbolic calculation Graphing with MathCAD Plotting vector against vector: The vectors must have equal number of elements. MathCAD plots values in its default units. To change units in the plot……? Divide your axis by the desired unit. Or remove the units from the defined vectors Use Graph Toolbox or [Shift-2] Or Insert/Graph from menu Graphing 1 20 2 28 time 3 min Temp 35 K time 4 42 Time min 5 49 40 40 Temp Temp 20 20 100 200 300 2 4 time Time Graphing with MathCAD 1 20 Plotting element by 2 28 element: define a time 3 min Temp 35 K 4 42 range variable 5 49 containing as many i 04 element as each of the vectors. 40 i:=0..4 Temp i 20 100 200 300 timei QuickPlots Use when you want to x 0 0.12 see what a function looks like 1 Create a x-y graph Enter the function on sin(x) 0 y-axis with parameter(s) 1 Enter the parameter on 0 2 4 6 x-axis x Graphing with MathCAD Plotting multiple curves:up to 16 curves in a single graph. Example: For 2 dependent variables (y) and 1 independent variable (x) Press shift2 (create a x-y plot) On the y axis enter the first y variable then press comma to enter the second y variable. On the x axis enter your x variable. -
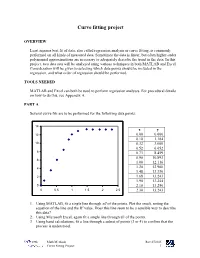
Curve Fitting Project
Curve fitting project OVERVIEW Least squares best fit of data, also called regression analysis or curve fitting, is commonly performed on all kinds of measured data. Sometimes the data is linear, but often higher-order polynomial approximations are necessary to adequately describe the trend in the data. In this project, two data sets will be analyzed using various techniques in both MATLAB and Excel. Consideration will be given to selecting which data points should be included in the regression, and what order of regression should be performed. TOOLS NEEDED MATLAB and Excel can both be used to perform regression analyses. For procedural details on how to do this, see Appendix A. PART A Several curve fits are to be performed for the following data points: 14 x y 12 0.00 0.000 0.10 1.184 10 0.32 3.600 0.52 6.052 8 0.73 8.459 0.90 10.893 6 1.00 12.116 4 1.20 12.900 1.48 13.330 2 1.68 13.243 1.90 13.244 0 2.10 13.250 0 0.5 1 1.5 2 2.5 2.30 13.243 1. Using MATLAB, fit a single line through all of the points. Plot the result, noting the equation of the line and the R2 value. Does this line seem to be a sensible way to describe this data? 2. Using Microsoft Excel, again fit a single line through all of the points. 3. Using hand calculations, fit a line through a subset of points (3 or 4) to confirm that the process is understood. -
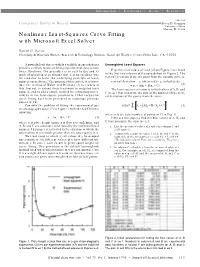
Nonlinear Least-Squares Curve Fitting with Microsoft Excel Solver
Information • Textbooks • Media • Resources edited by Computer Bulletin Board Steven D. Gammon University of Idaho Moscow, ID 83844 Nonlinear Least-Squares Curve Fitting with Microsoft Excel Solver Daniel C. Harris Chemistry & Materials Branch, Research & Technology Division, Naval Air Warfare Center,China Lake, CA 93555 A powerful tool that is widely available in spreadsheets Unweighted Least Squares provides a simple means of fitting experimental data to non- linear functions. The procedure is so easy to use and its Experimental values of x and y from Figure 1 are listed mode of operation is so obvious that it is an excellent way in the first two columns of the spreadsheet in Figure 2. The for students to learn the underlying principle of least- vertical deviation of the ith point from the smooth curve is squares curve fitting. The purpose of this article is to intro- vertical deviation = yi (observed) – yi (calculated) (2) duce the method of Walsh and Diamond (1) to readers of = yi – (Axi + B/xi + C) this Journal, to extend their treatment to weighted least The least squares criterion is to find values of A, B, and squares, and to add a simple method for estimating uncer- C in eq 1 that minimize the sum of the squares of the verti- tainties in the least-square parameters. Other recipes for cal deviations of the points from the curve: curve fitting have been presented in numerous previous papers (2–16). n 2 Σ Consider the problem of fitting the experimental gas sum = yi ± Axi + B / xi + C (3) chromatography data (17) in Figure 1 with the van Deemter i =1 equation: where n is the total number of points (= 13 in Fig. -

(EU FP7 2013 - 612218/3D-NET) 3DNET Sops HOW-TO-DO PRACTICAL GUIDE
3D-NET (EU FP7 2013 - 612218/3D-NET) 3DNET SOPs HOW-TO-DO PRACTICAL GUIDE Curve fitting This is intended to be an aid-memoir for those involved in fitting biological data to dose response curves in why we do it and how to best do it. So why do we use non linear regression? Much of the data generated in Biology is sigmoidal dose response (E/[A]) curves, the aim is to generate estimates of upper and lower asymptotes, A50 and slope parameters and their associated confidence limits. How can we analyse E/[A] data? Why fit curves? What’s wrong with joining the dots? Fitting Uses all the data points to estimate each parameter Tell us the confidence that we can have in each parameter estimate Estimates a slope parameter Fitting curves to data is model fitting. The general equation for a sigmoidal dose-response curve is commonly referred to as the ‘Hill equation’ or the ‘four-parameter logistic equation”. (Top Bottom) Re sponse Bottom EC50hillslope 1 [Drug]hillslpoe The models most commonly used in Biology for fitting these data are ‘model 205 – Dose response one site -4 Parameter Logistic Model or Sigmoidal Dose-Response Model’ in XLfit (package used in ActivityBase or Excel) and ‘non-linear regression - sigmoidal variable slope’ in GraphPad Prism. What the computer does - Non-linear least squares Starts with an initial estimated value for each variable in the equation Generates the curve defined by these values Calculates the sum of squares Adjusts the variables to make the curve come closer to the data points (Marquardt method) Re-calculates the sum of squares Continues this iteration until there’s virtually no difference between successive fittings. -

A Grid Algorithm for High Throughput Fitting of Dose-Response Curve Data Yuhong Wang*, Ajit Jadhav, Noel Southal, Ruili Huang and Dac-Trung Nguyen
Current Chemical Genomics, 2010, 4, 57-66 57 Open Access A Grid Algorithm for High Throughput Fitting of Dose-Response Curve Data Yuhong Wang*, Ajit Jadhav, Noel Southal, Ruili Huang and Dac-Trung Nguyen National Institutes of Health, NIH Chemical Genomics Center, 9800 Medical Center Drive, Rockville, MD 20850, USA Abstract: We describe a novel algorithm, Grid algorithm, and the corresponding computer program for high throughput fitting of dose-response curves that are described by the four-parameter symmetric logistic dose-response model. The Grid algorithm searches through all points in a grid of four dimensions (parameters) and finds the optimum one that corre- sponds to the best fit. Using simulated dose-response curves, we examined the Grid program’s performance in reproduc- ing the actual values that were used to generate the simulated data and compared it with the DRC package for the lan- guage and environment R and the XLfit add-in for Microsoft Excel. The Grid program was robust and consistently recov- ered the actual values for both complete and partial curves with or without noise. Both DRC and XLfit performed well on data without noise, but they were sensitive to and their performance degraded rapidly with increasing noise. The Grid program is automated and scalable to millions of dose-response curves, and it is able to process 100,000 dose-response curves from high throughput screening experiment per CPU hour. The Grid program has the potential of greatly increas- ing the productivity of large-scale dose-response data analysis and early drug discovery processes, and it is also applicable to many other curve fitting problems in chemical, biological, and medical sciences. -

Fitting Conics to Noisy Data Using Stochastic Linearization
Fitting Conics to Noisy Data Using Stochastic Linearization Marcus Baum and Uwe D. Hanebeck Abstract— Fitting conic sections, e.g., ellipses or circles, to LRF noisy data points is a fundamental sensor data processing problem, which frequently arises in robotics. In this paper, we introduce a new procedure for deriving a recursive Gaussian state estimator for fitting conics to data corrupted by additive Measurements Gaussian noise. For this purpose, the original exact implicit measurement equation is reformulated with the help of suitable Fig. 1: Laser rangefinder (LRF) scanning a circular object. approximations as an explicit measurement equation corrupted by multiplicative noise. Based on stochastic linearization, an efficient Gaussian state estimator is derived for the explicit measurement equation. The performance of the new approach distributions for the parameter vector of the conic based is evaluated by means of a typical ellipse fitting scenario. on Bayes’ rule. An explicit description of the parameter uncertainties with a probability distribution is in particular I. INTRODUCTION important for performing gating, i.e., dismissing unprobable In this work, the problem of fitting a conic section such measurements, and tracking multiple conics. Furthermore, as an ellipse or a circle to noisy data points is considered. the temporal evolution of the state can be captured with This fundamental problem arises in many applications related a stochastic system model, which allows to propagate the to robotics. A traditional application is computer vision, uncertainty about the state to the next time step. where ellipses and circles are fitted to features extracted A. Contributions from images [1]–[4] in order to detect, localize, and track objects. -

Investigating Bias in the Application of Curve Fitting Programs To
Atmos. Meas. Tech., 8, 1469–1489, 2015 www.atmos-meas-tech.net/8/1469/2015/ doi:10.5194/amt-8-1469-2015 © Author(s) 2015. CC Attribution 3.0 License. Investigating bias in the application of curve fitting programs to atmospheric time series P. A. Pickers and A. C. Manning Centre for Ocean and Atmospheric Sciences, School of Environmental Sciences, University of East Anglia, Norwich, NR4 7TJ, UK Correspondence to: P. A. Pickers ([email protected]) Received: 31 May 2014 – Published in Atmos. Meas. Tech. Discuss.: 16 July 2014 Revised: 6 November 2014 – Accepted: 6 November 2014 – Published: 23 March 2015 Abstract. The decomposition of an atmospheric time series programs for certain types of data sets, and for certain types into its constituent parts is an essential tool for identifying of analyses and applications. In addition, we recommend that and isolating variations of interest from a data set, and is sensitivity tests are performed in any study using curve fitting widely used to obtain information about sources, sinks and programs, to ensure that results are not unduly influenced by trends in climatically important gases. Such procedures in- the input smoothing parameters chosen. volve fitting appropriate mathematical functions to the data. Our findings also have implications for previous studies However, it has been demonstrated that the application of that have relied on a single curve fitting program to inter- such curve fitting procedures can introduce bias, and thus in- pret atmospheric time series measurements. This is demon- fluence the scientific interpretation of the data sets. We inves- strated by using two other curve fitting programs to replicate tigate the potential for bias associated with the application of work in Piao et al. -
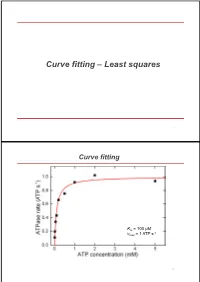
Curve Fitting – Least Squares
Curve fitting – Least squares 1 Curve fitting Km = 100 µM -1 vmax = 1 ATP s 2 Excurse error of multiple measurements Starting point: Measure N times the same parameter Obtained values are Gaussian distributed around mean with standard deviation σ What is the error of the mean of all measurements? Sum = x1 +x2 + ... + xN Variance of sum = N * σ2 (Central limit theorem) Standard deviation of sum N Mean = (x1 +x2 + ... + xN)/N N 1 Standard deviation of mean N (called standard error of mean) N N N 3 Excurse error propagation What is error for f(x,y,z,…) if we know errors of x,y,z,… (σx, σy, σz, …) for purely statistical errors? -> Individual variances add scaled by squared partial derivatives (if parameters are uncorrelated) Examples : Addition/substraction: squared errors add up squared relative Product: errors add up 4 Excurse error propagation squared relative Ratios: errors add up Powers: relative error times power Logarithms: error is relative error 5 Curve fitting – Least squares Starting point: - data set with N pairs of (xi,yi) - xi known exactly, -yi Gaussian distributed around true value with error σi - errors uncorrelated - function f(x) which shall describe the values y (y = f(x)) - f(x) depends on one or more parameters a [S] v vmax [S] KM 6 Curve fitting – Least squares 1 2 2 Probability to get y for given x [y i f (xi ;a)] / 2 i ] i i P(y i ;a) e 2 i [S] v vmax [S] KM 7 Curve fitting – Least squares N 1 2 2 Prob. -

Least Squares Analysis and Curve Fitting
This document downloaded from vulcanhammer.net vulcanhammer.info Chet Aero Marine Don’t forget to visit our companion site http://www.vulcanhammer.org Use subject to the terms and conditions of the respective websites. Fluid Mechanics Laboratory © Don C. Warrington ENCE 3070L http://chetaero.wordpress.com Least Squares Analysis and Curve Fitting Don C. Warrington Departments of Civil and Mechanical Engineering University of Tennessee at Chattanooga This is a brief overview of least squares analysis. It begins by explaining the difference between interplation and least squares analysis using basic linear algebra. From there vector norms and their relationship with the residual is discussed. Non-linear regression, such as is used with exponential and power regression, is explained. Finally a worked example is used to show the various regression schemes applied to a data set. Keywords: least squares, regression, residuals, linear algebra, logarithmic plotting Introduction We know we can define a line using two points. Work- ing in two dimensions, we can write these two equations as Curve fitting–particularly linear “curve” fitting–is a well follows: known technique among engineers and scientists. In the past the technique was generally applied graphically, i.e., the en- gineer or scientist would plot the points and then draw a “best y = mx + b (2) fit” line among the points, taking into consideration outliers, 1 1 etc. y2 = mx2 + b In reality, curve fitting is a mathematical technique which involves the solution of multiple equations, invoking the use In matrix form, this is of linear algebra and statistical considerations. This is the way a spreadsheet would look at the problem, and students 2 x 1 3 2 m 3 2 y 3 6 1 7 6 7 6 1 7 and practitioners alike utilize this tool without really under- 46 57 46 57 = 46 57 (3) standing how they do their job. -

Fitting Ellipses and General Second-Order Curves
Fitting Ellipses and General Second-Order Curves Gerald J. Agin July 31,1981 The Robotics Institute Carncgie-Mcllon University Pittsburgh, Pa. 15213 Preparation of this paper was supported by Westinghouse Corporation under a grant to thc Robotics Institute at Carncgie-Mcllon Univcrsity. 1 Abstract Many methods exist for fitting ellipses and other sccond-order curvcs to sets of points on the plane. Diffcrcnt methods use diffcrcnt measurcs for the goodness of fit of a given curve to a sct of points. The method most frequcntly uscd, minimization based on the general quadratic form, has serious dcficiencics. Two altcrnativc mcthods arc proposed: the first, bascd on an error measure divided by its average gradicnt, USCS an cigenvalue solution; the second is based on an error measure dividcd by individual gradients, and rcquircs hill climbing for its solution. As a corollary, a new method for fitting straight lincs to data points on the plane is presented. 2 Int I oduction 'I'his piper discusses the following problcm: Gicen some set of data points on thi. plmc, how slioultl we fit an cllipse to these points? In morc prccisc tcrms, let curvcs be rcprcscntcd by some equation G(x,j*)=O. Wc restrict C;(x,y) to he a polynomial in x and y of dcgrcc not grcatcr than 2. 'I'hc curves gcncratctl by such a runction arc thc conic scctiotis: cllipscs, hypcrlxhs. and parabolas. In the spccial cast whcl-e G( VJ) is of dcgrcc 1, thc curvc rcprcscntcd is a straight linc. Now, given a set of data pairs {(x,,ypi= 1,..., n), what is the hnction G(x.y) such that the curvc described by the equation best dcscribcs or fits thc data? 'f'he answcr to this question dcpcnds upon how wc define "best." Thc primary motivation for studying this problem is to dcal with systems that usc light stripcs to mcasure depth information [Agin 761 [Shirai] [Popplcstonc]. -

Curvefitting
309 Weitkunat, R. (ed.) Digital Biosignal Processing © 1991 Elsevier Science Publishers B. V. CHAPTER 13 Curvefitting A.T. JOHNSON University of Maryland, College Park, MD, USA Mathematical equations contain information in densely packed form. That is the single most important reason why data is often subjected to the process of curvefitting. Imagine having to describe the results of an experiment by publishing pages after pages of raw and derived data. Not only would careful study of the data be tedious and unlikely by any but the most dedicated, but data trends would be most difficult to discern. It may not be sufficient to know that as the data for the controlled variable increases, so does data for the output variable. How much of an increase is important? What is the shape of the increase? A mathematical expression can tell this at a glance. Mathematical equations remove undesired variations from data. Sources of these variations (often called ‘noise’ or ‘artifacts’) can range from strictly random thermodynamic events to systematic effects of electrical power-line magnetic and electrical fields. Everywhere in the building where I work, signals from a strong local radio station appear on sensitive electronic equipment. This adds considerably to the noise seen on our results, and strengthens the advantages of curvefitting. Mathematical equations can be used to derive theoretical implications concerning the underlying principles relating variables to one another. Biologists often express these relationships in exponential terms. Sometimes they use hyperbolas. Each of these carries with it a fundamental notion concerning the connection between one variable and another. There.is confidence that the relationship means more than just a blind attempt at describing data, and that interpolated or extrapolated values can be obtained without the expectation of too much error.