DOCSLIB.ORG

Applications of Derivatives: Displacement, Velocity and Acceleration

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Applications of Derivatives: Displacement, Velocity and Acceleration Applications of Derivatives: Displacement, Velocity and Acceleration Kinematics is the study of motion and is closely related to calculus. Physical quantities describing motion can be related to one another by derivatives. Below are some quantities that are used with the application of derivatives: 1. Displacement is the shortest distance between two positions and has a direction. Examples: - The park is 5 kilometers north of here - x(t) =5t, where x is displlaoement from a poiint P and tis time in seconds 2. Velocity refers to the speed and direction of an object. Examples: - Object moving 5 m/s backwards - v(t) = t2, where vis an object's v,elocity a11d t is time- in seconds 3. Acceleration is the rate of change of velocity per unit time. Imagine increasing your speed while driving. Acceleration is how quickly your speed changes every second. Examples: - Increasing speed from 10 m/s to 25 m/s in 5 s results in: 2S in/ :;=lOm/ :; 2 Accelerat ion = ----= 3 m/s 5s la(t) = -t. whem a is an object's accelerat1ion and tis time in seco11ds Displacement, velocity and acceleration can be expressed as functions of time. If we express these quantities as functions, they can be related by derivatives. Given x(t) as displacement, v(t) as velocity and a(t) as acceleration, we can relate the functions through derivatives. a(t) = 1l(t ) = x 11 (t) ©Tutoring and Learning Centre, George Brown College, 2020 | www.georgebrown.ca/tlc Equivalently, using Leibniz notation: ch, d 2 x .a(t) = -=­ dt dt2 The maximum of a motion function occurs when the first derivative of that function equals 0. For example, to find the time at which maximum displacement occurs, one must equate the first derivative of displacement (i.e. velocity) to zero. Notice on the right-hand graph, the maximum of the displacement function, x(t), occurs along the flat blue line where the rate of change is zero. X t 8 12 Example 1 If a particle iis moving ·n space with a velocity function, v(t) =t2-2.t-B where tis in seconds :3nd velociity is measured in meters per second: a) At what time(s), if any, is the particle at rest? b) What is the acceleration of the particle at t=3 seconds? Solution: a) If the particle is at rest, v(t)=0 (velocity is zero at rest) Solving for t when v(t) = 0: ©Tutoring and Learning Centre, George Brown College, 2020 | www.georgebrown.ca/tlc t2 - 2t - 8' = 0 (t - 4) (t + 2) = 0 t = 4 or t = -2 Since negative time is impossible, the only time at which the particle is at rest is 4 seconds. V b) First find the function for acceleration by taking the derivative of velocity. a(t) = v 1 (t ) a(t) = 2t - 2 Substitute t = 3 s in the acceleration function: a(3) = 2(3) - 2 = 4 m/s2 2 Thus, the acceleration at t = 3 s is 4 m/s . J,. Example 2 A soccer ball is kicked into the air so that the path of its flight can be modeled by the function, where t is in seconds and 푥 is meters above ground: ©Tutoring and Learning Centre, George Brown College, 2020 | www.georgebrown.ca/tlc ¥,{t) = - 4.9t2 +9.Bt + 5 a) At what time will the ball land? b) How many meters above ground was the ball kicked? c) What is the maximum height the ball will reach and at what time will this occur? d) What is the acceleration (with direction) of the ball at t=3 s? Solution: a) Since x(t) models height above ground, x(t)=0 when the ball hits the ground Solving fort when xtt) = 0: 0 = - 4.9t2 +9. Bf + 5 Sliinc e th is eql!.Jation cannot be factored, the quadratic equation must be used. - 9.8 ± .J 9.82 - 4( - 4.9) (5) t =---------- 2(-4.9) - 9.8 ± ✓ 1 94.04 =------ -9.8 t = 2-421 sort = -0.421 s (to 3 decimal places} ©Tutoring and Learning Centre, George Brown College, 2020 | www.georgebrown.ca/tlc However, t is greater than 0, (since time cannot be negative). Thus, the ball hits the ground 2.421 seconds after being launched. X mo, 8 6, 4 2 ' 2 t b) The initial height above ground occurs when t = 0. Substitute t = 0 into x(t): x(O) = -4_.9(0)2 + 9_8(0) + 5 = 5, Thus, the ball is thrown from 5 meters above ground. c) Maximum height occurs when the first derivative equals zero. ©Tutoring and Learning Centre, George Brown College, 2020 | www.georgebrown.ca/tlc Find the first derivat;iv,e: x'(t) = -9_8t + 9_8 Solve for t when xlt) = 0, ·~ime when the ball reaches maximum height: 0 = -9_8t + 9_8 -9_8! = -9-8 t = 1 s Substitute t = 1 s into x{t): ~ 11) = - 4_9(1)2 +9'_8(1) + 5 = g_g m Tilus , ~he maximum height is 9_9 m_ d) Acceleration is equal to the second derivative of displacement. Fiindiing second derivative: x''(t) = -9.8 Acceleratiion iis constant for all values of time, Thus, x:{3)1 = -9.8. t. Thus, the acceleration of the ball at 3 seconds is 9.8 m/s2 [down]. The negative implies that the acceleration is downward. The acceleration of the ball equals the acceleration of gravity: 9.8 m/s2 [down]. This is because the ball is subject to gravity at all times during its flight. t ©Tutoring and Learning Centre, George Brown College, 2020 | www.georgebrown.ca/tlc Exercises: Problem 1: If a partide moves in space according to the function x(t) = t3-4t2, whem t is time in seconds and x i1s displacement from the origin in oentimeters (with positive to the right): a) Find the acceleration of the particle at t = 2 s. b) Determine at what displacement(s) from the origin the particle is at rest. c) Find the maximum velocity of the particle. Problem 2: An ,electron moves such that its velocity function with respect to time is v(f)=.e2t-2, where tis time in seconds and vis velociity in meters per second: a) What is the acceleration of the electron at t = 10 s? b) Is the electron ever at rest? Algebraically explain why or why not. Problem 3: A balll iis thrown in the air and follows the displacement function x(t) = -4.9t2 + 4.9t + 9.8 , where tis time iin seconds and x is displlacement above the ground in meters: a) What is the initial height (above ground) from which the ball is thrown? b) At what time does the ball reach its maximum height? What is the maximum height above ground? c) Determine when the ball hits the ground? d) What is the acceleration of the ball at t = 1 s, t = 1.5 s and t = 2s? What do you notice? Solutions: 1a) 4 m/s2 [right]: 1b) .At origin and 256/27 cm [left of origiin] 2 1c) 16/3 m/s [left] 2a) 2e18 mi s~ 2b) Never, e2t-2=0 has no sollution ©Tutoring and Learning Centre, George Brown College, 2020 | www.georgebrown.ca/tlc 3a) 9.8 m; t = 0.5 s arid x(0.5)=11 .025 m 3c) t = 2s; 3d) -9.8 m/s2 (constant due to gravity) ©Tutoring and Learning Centre, George Brown College, 2020 | www.georgebrown.ca/tlc .
Load more

Recommended publications
  • Position, Displacement, Velocity Big Picture
    Position, Displacement, Velocity Big Picture I Want to know how/why things move I Need a way to describe motion mathematically: \Kinematics" I Tools of kinematics: calculus (rates) and vectors (directions) I Chapters 2, 4 are all about kinematics I First 1D, then 2D/3D I Main ideas: position, velocity, acceleration Language is crucial Physics uses ordinary words but assigns specific technical meanings! WORD ORDINARY USE PHYSICS USE position where something is where something is velocity speed speed and direction speed speed magnitude of velocity vec- tor displacement being moved difference in position \as the crow flies” from one instant to another Language, continued WORD ORDINARY USE PHYSICS USE total distance displacement or path length traveled path length trav- eled average velocity | displacement divided by time interval average speed total distance di- total distance divided by vided by time inter- time interval val How about some examples? Finer points I \instantaneous" velocity v(t) changes from instant to instant I graphically, it's a point on a v(t) curve or the slope of an x(t) curve I average velocity ~vavg is not a function of time I it's defined for an interval between instants (t1 ! t2, ti ! tf , t0 ! t, etc.) I graphically, it's the \rise over run" between two points on an x(t) curve I in 1D, vx can be called v I it's a component that is positive or negative I vectors don't have signs but their components do What you need to be able to do I Given starting/ending position, time, speed for one or more trip legs, calculate average
    [Show full text]
  • Oscillations
    CHAPTER FOURTEEN OSCILLATIONS 14.1 INTRODUCTION In our daily life we come across various kinds of motions. You have already learnt about some of them, e.g., rectilinear 14.1 Introduction motion and motion of a projectile. Both these motions are 14.2 Periodic and oscillatory non-repetitive. We have also learnt about uniform circular motions motion and orbital motion of planets in the solar system. In 14.3 Simple harmonic motion these cases, the motion is repeated after a certain interval of 14.4 Simple harmonic motion time, that is, it is periodic. In your childhood, you must have and uniform circular enjoyed rocking in a cradle or swinging on a swing. Both motion these motions are repetitive in nature but different from the 14.5 Velocity and acceleration periodic motion of a planet. Here, the object moves to and fro in simple harmonic motion about a mean position. The pendulum of a wall clock executes 14.6 Force law for simple a similar motion. Examples of such periodic to and fro harmonic motion motion abound: a boat tossing up and down in a river, the 14.7 Energy in simple harmonic piston in a steam engine going back and forth, etc. Such a motion motion is termed as oscillatory motion. In this chapter we 14.8 Some systems executing study this motion. simple harmonic motion The study of oscillatory motion is basic to physics; its 14.9 Damped simple harmonic motion concepts are required for the understanding of many physical 14.10 Forced oscillations and phenomena. In musical instruments, like the sitar, the guitar resonance or the violin, we come across vibrating strings that produce pleasing sounds.
    [Show full text]
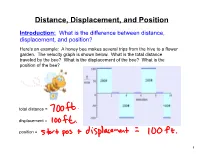
  • Distance, Displacement, and Position
    Distance, Displacement, and Position Introduction: What is the difference between distance, displacement, and position? Here's an example: A honey bee makes several trips from the hive to a flower garden. The velocity graph is shown below. What is the total distance traveled by the bee? What is the displacement of the bee? What is the position of the bee? total distance = displacement = position = 1 Warm-up A particle moves along the x-axis so that the acceleration at any time t is given by: At time , the velocity of the particle is and at time , the position is . (a) Write an expression for the velocity of the particle at any time . (b) For what values of is the particle at rest? (c) Write an expression for the position of the particle at any time . (d) Find the total distance traveled by the particle from to . 2 Warm-up Answers (a) (b) (c) (d) Total Distance = 3 Now, using the equation from the warm-up find the following (WITHOUT A CALCULATOR): (a) the total distance from 0 to 4 (b) the displacement from 0 to 4 4 To find the displacement (position shift) from the velocity function, we just integrate the function. The negative areas below the x-axis subtract from the total displacement. Displacement = To find the distance traveled we have to use absolute value. Distance traveled = To find the distance traveled by hand you must: Find the roots of the velocity equation and integrate in pieces, just like when we found the area between a curve and x-axis.
    [Show full text]
  • Force-Based Element Vs. Displacement-Based Element
    Force-based Element vs. Displacement-based Element Vesna Terzic UC Berkeley December 2011 Agenda • Introduction • Theory of force-based element (FBE) • Theory of displacement-based element (DBE) • Examples • Summary and conclusions • Q & A with web participants Introduction • Contrary to concentrated plasticity models (elastic element with rotational springs at element ends) force-based element (FBE) and displacement- based element (DBE) permit spread of plasticity along the element (distributed plasticity models). • Distributed plasticity models allow yielding to occur at any location along the element, which is especially important in the presence of distributed element loads (girders with high gravity loads). Introduction • OpenSees commands for defining FBE and DBE have the same arguments: element forceBeamColumn $eleTag $iNode $jNode $numIntgrPts $secTag $transfTag element displacementBeamColumn $eleTag $iNode $jNode $numIntgrPts $secTag $transfTag • However a beam-column element needs to be modeled differently using these two elements to achieve a comparable level of accuracy. • The intent of this seminar is to show users how to properly model frame elements with both FBE and DBE. • In order to enhance your understanding of these two elements and to assure their correct application I will present the theory of these two elements and demonstrate their application on two examples. Transformation of global to basic system Element u p u p p aT q v = af u GeometricTran = f q3,v3 q1,v1 v q Basic System q2,v 2 Displacement-based element • The displacement-based approach follows standard finite element procedures where we interpolate section deformations from an approximate displacement field then use the PVD to form the element equilibrium relationship.
    [Show full text]
  • Angular Kinematics Contents of the Lesson
    Angular Kinematics Contents of the Lesson Angular Motion and Kinematics Angular Distance and Angular Displacement. Angular Speed and Angular Velocity Angular Acceleration Questions. Motion “change in the position of an object with respect to some reference frame.” Planes and Axis. Angular Motion “Rotation of a object around a central imaginary line” Characteristics: ◦ Axis of rotation. ◦ Whole object moves. Identify the angular motion Angular motion in the human body “most of movement are angular” In the human body; ◦ Joint= Axis of rotation. ◦ Body segment= object or rotatory body. ◦ Initial position= anatomical position. Kinematics; Angular Kinematics “Description of Angular Motion” Seeks to answer? “How much something has rotated?” “How fast something is rotating?” etc. Units of measurements Degrees. Radian Units of measurement Revolutions 1 revolution= 1 circle= 360 degrees= 2휋.radians Angular Distance “Sum of all angular changes undergone by a rotatory body” Unit: degrees, radian revolution. Angular Displacement “difference between the initial and final position of a rotatory body around an axis of rotation with regards to direction.” Direction= counter clockwise or clockwise In Human movement= Flexion,Extension,etc. What will be the angular displacement? Angular Speed “Scalar quantity” “angular distance covered divided by time interval over which the motion occurred” Angular Velocity “Vector quantity” “rate of change of angular position or angular displacement w.r.t time” Angular speed and Velocity Angular speed = degree/sec, rad/sec, or revolution/sec. Angular Velocity= degree/sec, rad/sec, or revolution/sec counterclockwise, clockwise or flexion or extension, etc. Angular Acceleration “Rate of change of angular velocity w.r.t time.” Unit= degree/sec² Calculate acceleration.
    [Show full text]
  • Analysis on Torque, Flowrate, and Volumetric Displacement of Gerotor Pump/Motor
    연구논문 Journal of Drive and Control, Vol.17 No.2 pp.28-37 Jun. 2020 ISSN 2671-7972(print) ISSN 2671-7980(online) http://dx.doi.org/10.7839/ksfc.2020.17.2.028 Analysis on Torque, Flowrate, and Volumetric Displacement of Gerotor Pump/Motor Hongsik Yun1, Young-Bog Ham2 and Sungdong Kim1* Received: 02 Apr. 2020, Revised: 14 May 2020, Accepted: 18 May 2020 Key Words：Torque Equilibrium, Energy Conservation, Volumetric Displacement, Flowrate, Rotation Speed, Gerotor Pump/Motor Abstract: It is difficult to analytically derive the relationship among volumetric displacement, flowrate, torque, and rotation speed regarding an instantaneous position of gerotor hydraulic pumps/motors. This can be explained by the geometric shape of the rotors, which is highly complicated. Herein, an analytical method for the instantaneous torque, rotation speed, flowrate, and volumetric displacement of a pump/motor is proposed. The method is based on two physical concepts: energy conservation and torque equilibrium. The instantaneous torque of a pump/motor shaft is determined for the posture of rotors from the torque equilibrium. If the torque equilibrium is combined with the energy conservation between the hydraulic energy of the pump/motor and the mechanical input/output energy, the formula for determining the instantaneous volumetric displacement and flowrate is derived. The numerical values of the instantaneous volumetric displacement, torque, rotation speed, and flowrate are calculated via the MATLAB software programs, and they are illustrated for the case in which inner and outer rotors rotate with respect to fixed axes. The degrees of torque fluctuation, speed fluctuation, and flowrate fluctuation can be observed from their instantaneous values.
    [Show full text]
  • Hydraulophone Design Considerations: Absement, Displacement, and Velocity-Sensitive Music Keyboard in Which Each Key Is a Water Jet
    Hydraulophone Design Considerations: Absement, Displacement, and Velocity-Sensitive Music Keyboard in which each key is a Water Jet Steve Mann, Ryan Janzen, Mark Post University of Toronto, Dept. of Electrical and Computer Engineering, Toronto, Ontario, Canada For more information, see http://funtain.ca ABSTRACT General Terms We present a musical keyboard that is not only velocity- Measurement, Performance, Design, Experimentation, Hu- sensitive, but in fact responds to absement (presement), dis- man Factors, Theory placement (placement), velocity, acceleration, jerk, jounce, etc. (i.e. to all the derivatives, as well as the integral, of Keywords displacement). Fluid-user-interface, tangible user interface, direct user in- Moreover, unlike a piano keyboard in which the keys reach terface, water-based immersive multimedia, FUNtain, hy- a point of maximal displacement, our keys are essentially draulophone, pneumatophone, underwater musical instru- infinite in length, and thus never reach an end to their key ment, harmelodica, harmelotron (harmellotron), duringtouch, travel. Our infinite length keys are achieved by using water haptic surface, hydraulic-action, tracker-action jet streams that continue to flow past the fingers of a per- son playing the instrument. The instrument takes the form 1. INTRODUCTION: VELOCITY SENSING of a pipe with a row of holes, in which water flows out of KEYBOARDS each hole, while a user is invited to play the instrument by High quality music keyboards are typically velocity-sensing, interfering with the flow of water coming out of the holes. i.e. the notes sound louder when the keys are hit faster. The instrument resembles a large flute, but, unlike a flute, Velocity-sensing is ideal for instruments like the piano, there is no complicated fingering pattern.
    [Show full text]
  • Force Transmissibility Versus Displacement Transmissibility
    Journal of Sound and Vibration ] (]]]]) ]]]–]]] Contents lists available at ScienceDirect Journal of Sound and Vibration journal homepage: www.elsevier.com/locate/jsvi Force transmissibility versus displacement transmissibility Y.E. Lage a, M.M. Neves a,n, N.M.M. Maia a, D. Tcherniak b a LAETA, IDMEC, Instituto Superior Técnico, Universidade de Lisboa, Av. Rovisco Pais 1, 1049-001 Lisboa, Portugal b Brüel & Kjaer Sound and Vibration Measurement A/S, Skodsborgvej 307, DK 2850 Naerum, Denmark article info abstract Article history: It is well-known that when a single-degree-of-freedom (sdof) system is excited by a Received 5 June 2013 continuous motion of the foundation, the force transmissibility, relating the force transmitted Received in revised form to the foundation to the applied force, equals the displacement transmissibility. Recent 18 May 2014 developments in the generalization of the transmissibility to multiple-degree-of-freedom Accepted 19 May 2014 (mdof) systems have shown that similar simple and direct relations between both types of Handling Editor: H. Ouyang transmissibility do not appear naturally from the definitions, as happens in the sdof case. In this paper, the authors present their studies on the conditions under which it is possible to establish a relation between force transmissibility and displacement transmissibility for mdof systems. As far as the authors are aware, such a relation is not currently found in the literature, which is justified by being based on recent developments in the transmissibility concept for mdof systems. Indeed, it does not appear naturally, but the authors observed that the needed link is present when the displacement transmissibility is obtained between the same coordinates where the applied and reaction forces are considered in the force transmissibility case; this implies that the boundary conditions are not exactly the same and instead follow some rules.
    [Show full text]
  • Rotation: Kinematics
    Rotation: Kinematics Rotation refers to the turning of an object about a fixed axis and is very commonly encountered in day to day life. The motion of a fan, the turning of a door knob and the opening of a bottle cap are a few examples of rotation. Rotation is also commonly observed as a component of more complex motions that result as a combination of both rotation and translation. The motion of a wheel of a moving bicycle, the motion of a blade of a moving helicopter and the motion of a curveball are a few examples of combined rotation and translation. This module focuses on the kinematics of pure rotation. This module begins by defining the angular variables and then proceeds to describe the relation between these variables and the variables of linear motion. Angular Variables Angular Position Consider an object rotating about a fixed axis. Let us define a coordinate system such that the axis of rotation passes through the origin and is perpendicular to the x- and y- axes. Fig. 1 shows a view of the x-y plane. If a reference line is drawn through the origin and a fixed point in the object, the angle between this line and a fixed direction is used to define the angular position of the object. In Fig. 1, the angular position is measured from the positive x-direction. Fig. 1: Rotating object - Angular position. Also, from geometry, the angular position can be written as the ratio of the length of the path traveled by any point on the reference line measured from the fixed direction to the radius of the path, ...Eq.
    [Show full text]
  • Design of Force Versus Displacement Test Stand
    Western Michigan University ScholarWorks at WMU Honors Theses Lee Honors College 4-17-2018 Design of Force Versus Displacement Test Stand Andrew Fritchley Western Michigan University, [email protected] Follow this and additional works at: https://scholarworks.wmich.edu/honors_theses Part of the Electro-Mechanical Systems Commons Recommended Citation Fritchley, Andrew, "Design of Force Versus Displacement Test Stand" (2018). Honors Theses. 2945. https://scholarworks.wmich.edu/honors_theses/2945 This Honors Thesis-Open Access is brought to you for free and open access by the Lee Honors College at ScholarWorks at WMU. It has been accepted for inclusion in Honors Theses by an authorized administrator of ScholarWorks at WMU. For more information, please contact [email protected]. Design of Force Versus Displacement Test Stand Andrew Fritchley Drew Arndt Fabian Venegas Group: 04-18-20 Faculty Mentor: Dr. Ghantasala Industrial Mentor: David Phaneuf 11 April 2018 1 Disclaimer This project report was written by students at Western Michigan University to fulfill an engineering curriculum requirement. Western Michigan University makes no representation that the material contained in the report is error-free or complete in all respects. Persons or organizations who choose to use the material do so at their own risk 2 Abstract Performing mechanical design around sensors is a critical skill which all engineering students should be familiar with. Of equal importance is gathering and correctly interpreting electrical data from engineering tests. The aim of this project is to design a force versus displacement test stand for applications related to the measurement of spring force-displacement correlation. The design uses a strain gauge load cell, and a magnetic linear encoder to provide accurate, repeatable force and travel measurements.
    [Show full text]
  • Displacement, Velocity, and Acceleration
    Displacement, Velocity, and Acceleration (WHERE and WHEN?) I’m not going to teach you anything today that you don’t already know! (basically) Practice: 7.1, 7.5, 7.7, 7.9, 7.11, 7.13 Do you guys remember this background slide? I wanted to show you where you started from to inspire you: we’ve learned a lot and most of you are doing great! Mid-semester grades have been submitted, by the way. Notes • Thanks for your feedback! • I will state clicker answers clearly. Remind me if I don’t! • I will try to write bigger on light board! If things are still too small, please do me and you a favor and speak up during class! There will be zero people mad at you. Displacement, Velocity, and Acceleration (WHERE and WHEN?) The other reason I wanted to show you this was to remind you that when we did linear motion, first we developed the equations of motion. Then we discussed the forces that cause this motion. We’re going to do something very similar now, and develop the same things for ROTATION. *Angular* Displacement, Velocity, and Acceleration (WHERE and WHEN?) Rotational motion has to do with anything spinning… Earth Tires Disks What you’ll be doing… • Unit conversion (degrees, radians, revs). • Angular position, velocity, acceleration. • Convert between angular and linear quantities. Linear motion Angular motion Displacement, Δx Δθ Angular displacement Velocity, v ω Angular velocity Acceleration, a α Angular acceleration v = v0 + at ω = ω0 + αt 2 2 Δx = v0t + ½ at Δθ = ωt + ½ αt 2 2 2 2 v = v0 + 2aΔx ω = ω0 + 2αΔθ The rotational motion equations look like weird cousins of the usual kinematics equations.
    [Show full text]
  • Position, Displacement, Velocity, & Acceleration Vectors Chap. 3
    General Physics (PHY 170) Chap. 3 Position, Displacement, Velocity, & Acceleration Vectors 1 Motion in Two Dimensions Using + or – signs is not always sufficient to fully describe motion in more than one dimension Vectors can be used to more fully describe motion: displacement, velocity, and acceleration 2 Position, Displacement, Velocity, & Acceleration Vectors The position vector r points from the origin to the location in question. The displacement vector Δr points from the original position to the final position. 3 The Displacement Vector r = Xx^ + Yy^ Δr = r2 -r1 = = (X2x^ +Y2y)^ - (X1x^ + Y1y)^ = Δxx^ + Δyy^ 4 The Average Velocity Vector Average velocity vector: is the ratio of the displacement to the time interval for the displacement Vav is in the same direction as Δr. 5 The Instantaneous Velocity Vectors Instantaneous velocity vector: is the limit of the average velocity as Δt approaches zero. Its direction is along a line that is tangent to the path of the particle and in the direction of motion. 6 Velocity Vectors 7 Example: Velocity of a Sailboat A sailboat has coordinates (130 m, 205 m) at t1=0.0 s. Two minutes later its position is (110 m, 218 m). (a) Find vav; (b) Find |vav|; | | 8 Example: A Dragonfly A dragonfly is observed initially at position: Three seconds later, it is observed at position: What was the dragonfly’s average velocity during this time? 9 Acceleration Vectors The average acceleration vector: is defined as the rate at which the velocity changes. It is in the direction of the change in velocity Δv. The instantaneous acceleration is the limit of the average acceleration as Δt approaches zero.
    [Show full text]