Download File
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

I-35W Mississippi River Bridge Failure – Is It a Wake up Call?
Point of View These columns of ICJ offer an opportunity to the engineering fraternity to express their views on the current practices in design, construction and management being followed in the industry. To share your opinion with our readers, you may send in your inputs in about 1500 words via e-mail to [email protected] I-35W Mississippi river bridge failure – Is it a wake up call? N. Subramanian Infrastructure plays a major role in the economy of 1907, the Tacoma Narrows in 1940 and the West Gate a country. Bridges are a major component of any in 1970. Whether this theory will hold well in the near infrastructure and the failure of a bridge will affect the future is debatable as many of the aging infrastructure economy of any country. The recent failure of the I-35W projects in several countries are under threat of failure Mississippi river bridge may be considered as a wake and some immediate measures are necessary to save up call to think about redundancy in structural design them from disasters. This paper discusses the recent of bridges, and evolution of bridge monitoring and failure of I-35 W Mississippi river bridge and gives some inspection systems. The details of the I-35W Mississippi details of other major bridge failures. river bridge, its failure and its impact on future bridge designs, monitoring and testing are discussed in this The I-35W Mississippi river bridge paper. These details may help in preventing such The I-35W Mississippi river bridge (officially designated disastrous failures in future. -

So Now I²ll Count from Ìve to One and Bring You out of This
Media. Memory. Meme. Colin Bennett. Prime Time. ! !" #" $" #" %" &" '" ( =5#'5/# ">00# .56')# !"#$%#&'#$#($)*+(# ,+-+(+#.(&,&,#/&)*# )*+#$0&+',1#"#/&00# 8(5%# 2+#)$03&'4#)5#)*+%# )5'&4*)#$256)#%7# 86)6(+#$'9#/*$)# ?-+#)5# )*+7#/&00#5(#/&00# '5)#95#)5#%+1: 5'+# ;$-&9#<$.52, $'9# 2(&'4# 756# 56)#58# )*&,1 ")*("+,-(#."+/ 0!!#"1++-2 !"#$$%&'()*+ Vol. 24 No. 1 Issue # 154 !"#"$%&'()*+(,-./01** UFO Volume 24 • Number 1 columnists 6 Publisher’s Note: William J. Birnes 7 Saucers, Slips & Cigarettes: Dierdre O’Lavery 8 Rocket Scientist: Stanton T. Friedman 10 Outside the Box: Mike Good 12 Opinionated Oregonian: George W. Earley 14 Alien in the Attic: Farah Yurdözü 16 Coast to Coast AM: George Noory 17 An Alien View: Alfred Lehmberg 18 The Randle Report: Kevin D. Randle 20 21st Century News: Dr. Bob & Zohara Hieronimus 22 Truthseeking: Dennis Balthaser 24 Inner Space: Sri Ram Kaa and Kira Raa 26 View From A Brit: Nick Redfern 27 Bryant’s UFO View: Larry W. Bryant 28 The Orange Orb: Regan Lee 29 Beyond the Dial: Lesley Gunter 30 Mirror Images: Micah A. Hanks bits & bobs 32 Arlan’s Arcanae: Arlan Andrews, Sr. Say hello to Dierdre! She is a 74 Rick’s UFO Picks: Rick Troppman new columnist, she is on page 7, and she is sassy. To Alfred Lehmberg: A belated thank you for the great cover artwork of Richard toon Dolan in Issue #153. Thanks also must go to our 63 Bradley Peterson very very very patient readers. This issue has been a long time coming. Next one should be just a bit more prompt. UFO Issue 154 features 34 Aliens vs. -

Directions & Travel Guide
Accommodations Rio Grande Directory Travel Guide Rio Grande/Gallipolis • Athletic Director: Jeff Lanham Office: 740-245-7485 Cell: 740-441-5742 • Best Western e-mail: [email protected] 918 Second Ave. Gallipolis, OH 45631 ............... 740-446-3373 • Athletic Department Secretary: Wendy Hammons Office: 740-245-7293 Directions to Rio Grande • Hampton Inn Fax: 740-245-7555 444 State Route 7 N From Lexington, KY: (181 miles) Take I-64 Gallipolis, OH 45631 ............... 740-446-8000 • Sports Information Director: Randy Payton East toward Ashland. Exit off 64 East at the Office: 740-245-7213 Cell: 740-339-3632 Barboursville exit (EXIT 18) to Route 60/ • Quality Inn e-mail: [email protected] Route 2 North to Point Pleasant. Take US-35 577 State Route 7 N toward Chillicothe (cross bridge into Ohio). Gallipolis, OH 45631 ............... 740-446-0090 • Baseball Head Coach: Brad Warnimont Take the OH-325 exit toward Vinton/Rio Office: 740-245-7486 Cell: 740-208-7425 Grande and turn left. • Regency Inn e-mail: [email protected] 151 Upper River Road From Cincinnati: (131.66 miles) Take OH-32 Gallipolis, OH 45631 ................740-446-0241 • Men’s Basketball Head Coach: Ken French East toward Batavia. Merge of US 35 E. Take Office: 740-245-7294 Cell: 740-645-3035 the OH-325 Exit toward Vinton/Rio Grande • Riverside Motel e-mail: [email protected] and turn right. 1066 First Avenue Gallipolis, OH 45631 ...............740-446 -2702 • Women’s Basketball Head Coach: David Smalley From Columbus: (94.64 miles) Take I-270 Office: 740-245-7491 Cell: 740-709-4971 East (EXIT 101) toward Wheeling. -

Visit Ohio's Historic Bridges
SPECIAL ADVERTISING SECTION Visit Ohio’s Historic Bridges Historic and unique bridges have a way of sticking in our collective memories. Many of us remember the bridge we crossed walking to school, a landmark on the way to visit relatives, the gateway out of town or a welcoming indication that you are back in familiar territory. The Ohio Department of Transportation, in collaboration with the Ohio Historic Bridge Association, Ohio History Connection’s State Historic Preservation Office, TourismOhio and historicbridges.org, has assembled a list of stunning bridges across the state that are well worth a journey. Ohio has over 500 National Register-listed and historic bridges, including over 150 wooden covered bridges. The following map features iron, steel and concrete struc- tures, and even a stone bridge built when canals were still helping to grow Ohio’s economy. Some were built for transporting grain to market. Other bridges were specifically designed to blend into the scenic landscape of a state or municipal park. Many of these featured bridges are Ohio Historic Bridge Award recipients. The annual award is given to bridge owners and engineers that rehabilitate, preserve or reuse historic structures. The awards are sponsored by the Federal Highway Administration, ODOT and Ohio History Connection’s State Historic Preservation Office. Anthony Wayne Bridge - Toledo, OH Ohio Department of Transportation SPECIAL ADVERTISING SECTION 2 17 18 SOUTHEAST REGION in eastern Ohio, Columbiana County has Metropark’s Huntington Reservation on the community. A project that will rehabilitate several rehabilitated 1880’s through truss shore of Lake Erie along US 6/Park Drive. -

INSPIRE Newsletter Fall 2020
Missouri University of Science and Technology Scholars' Mine INSPIRE Newsletters INSPIRE - University Transportation Center Fall 2020 INSPIRE Newsletter Fall 2020 Missouri University of Science and Technology. INSPIRE - University Transportation Center Follow this and additional works at: https://scholarsmine.mst.edu/inspire-newsletters Part of the Structural Engineering Commons Recommended Citation Missouri University of Science and Technology. INSPIRE - University Transportation Center, "INSPIRE Newsletter Fall 2020" (2020). INSPIRE Newsletters. 8. https://scholarsmine.mst.edu/inspire-newsletters/8 This Newsletter is brought to you for free and open access by Scholars' Mine. It has been accepted for inclusion in INSPIRE Newsletters by an authorized administrator of Scholars' Mine. This work is protected by U. S. Copyright Law. Unauthorized use including reproduction for redistribution requires the permission of the copyright holder. For more information, please contact [email protected]. TIER 1 UNIVERSITY TRANSPORTATION CENTER (UTC) Sponsored by the Office of the Assistant Secretary for Research and Technology in the U.S. Department of Transportation INSPECTING AND PRESERVING INFRASTRUCTURE THROUGH ROBOTIC EXPLORATION VOL. 4 | ISSUE 2 | (FALL) INSPIRE-UTC Biannual Publication Director’s Message Greetings colleagues and friends! Since our last newsletter, the INSPIRE UTC has held In this issue: a virtual annual meeting with its members and a graduate student poster competition. The center continues to host webinars on a quarterly basis, engaging attendees world- Director's Message wide on infrastructure and transportation related topics. Kummer Institute Donors In the largest single gift in the history of Missouri higher edu- cation, St. Louis businessman Fred Kummer and his wife June News have donated $300 million to a foundation that will support Forensic Bridge Research Missouri S&T. -

Framework for Improving Resilience of Bridge Design
U.S. Department of Transportation Federal Highway Administration Framework for Improving Resilience of Bridge Design Publication No. FHWA-IF-11-016 January 2011 Notice This document is disseminated under the sponsorship of the U.S. Department of Transportation in the interest of information exchange. The U.S. Government assumes no liability for use of the information contained in this document. This report does not constitute a standard, specification, or regulation. Quality Assurance Statement The Federal Highway Administration provides high-quality information to serve Government, industry, and the public in a manner that promotes public understanding. Standards and policies are used to ensure and maximize the quality, objectivity, utility, and integrity of its information. FHWA periodically reviews quality issues and adjusts its programs and processes to ensure continuous quality improvement. Framework for Improving Resilience of Bridge Design Report No. FHWA-IF-11-016 January 2011 Technical Report Documentation Page 1. Report No. 2. Government Accession No. 3. Recipient’s Catalog No. FHWA-IF-11-016 4. Title and Subtitle 5. Report Date Framework for Improving Resilience of Bridge Design January 2011 6. Performing Organization Code 7. Author(s) 8. Performing Organization Report No. Brandon W. Chavel and John M. Yadlosky 9. Performing Organization Name and Address 10. Work Unit No. HDR Engineering, Inc. 11 Stanwix Street, Suite 800 11. Contract or Grant No. Pittsburgh, Pennsylvania 15222 12. Sponsoring Agency Name and Address 13. Type of Report and Period Covered Office of Bridge Technology Technical Report Federal Highway Administration September 2007 – January 2011 1200 New Jersey Avenue, SE Washington, D.C. 20590 14. -

Engineering Ethics: Three Case Studies
ENGINEERING ETHICS: THREE CASE STUDIES (Subtitle: EVERYTHING SHOULD BE AS SIMPLE AS POSSIBLE, BUT NOT SIMPLER) Victor Singer, P.E. (retired) Dan Schiffbauer, P.E. Toshiba OVERVIEW: • Canons or Codes of Ethics • Noteworthy Historical Background for Each Case In Point – The Tacoma Narrows First Suspension Bridge: failed 1940 – The Silver Bridge (US Hwy 35 Ohio River Crossing): failed 1967 – The Shuttle Challenger: failed 1986 • Questions To Ponder For Each Case In Point: – Are There Relevant Ethical Issues Or Just 20-20 Hindsight? – When, If At All, Did Which Ethical Issue Come Into Play? – If Errors Occurred, Were They Errors Of Judgment, Omission or Commission? – Or Murphy’s Law Events - - Accidents In An Imperfectly Understood World? – Who Should Have Done What, That He Didn't Do? CANONS OR CODES OF ETHICS • NSPE, ASCE, ASME, AAES: Engineers shall hold paramount the safety, health and welfare of the public . (Fundamental Canon) • AIChE: Members shall hold paramount the safety, health and welfare of the public . • IEEE: We, the members of the IEEE . , do hereby . agree to accept responsibility in making decisions consistent with the safety, health and welfare of the public . • AIAA: The AIAA member will have proper regard for the safety, health and welfare of the public in the performance of his professional duties. • AIA: Members should . thoughtfully consider the social and environmental impact of their professional activities. • ABA Model Code of Professional Responsibility: Canons: 1. A lawyer should assist in maintaining the integrity and competence of the legal profession. 2. A lawyer should assist the legal profession in its duty to make legal counsel available. -

민⋅관 거버넌스를 통한 교량안전관리 개선에 관한 연구 a Study on the Improvement Program of Bridge Safety Management Through Public-Private Governance
J. Korean Soc. Hazard Mitig. ISSN 1738-2424(Print) Vol. 18, No. 1 (Jan. 2018), pp.145~156 ISSN 2287-6723(Online) https://doi.org/10.9798/KOSHAM.2018.18.1.145 www.kosham.or.kr 등재 민⋅관 거버넌스를 통한 교량안전관리 개선에 관한 연구 A Study on the Improvement Program of Bridge Safety Management Through Public-Private Governance 김성제*·윤명오** Kim, Seong Jeh*, and Yoon, Myong O** Abstract Unsafe accidents occurred such as the collapse of Seongsoo Bridge in October 1994 and the collapse of Sampoong Department Store in June 1995, in the wake of the dynamic urban infrastructure & economic growth policy in the 1960s and thereafter. Following the collapse of the Seongsu Bridge, enacting in accordance with established regulations of ≷Misfortune and the safety supervision basic law≸ & ≷Special Act on Safety Management of Building Structures≸, regular safety inspection and diagnosis of routine was enforced. However, the bridge safety accident has remained constant since then, and the bridge safety management system is still insufficient compared to the developed nations. Based on advanced cases of bridge accidents in the developed countries (United States and Japan), this research suggest the best practices of the maintenance system, and development measures are provided to improve the safety management of bridges through governance. These are as follows. Innovation of bridge management policies through Bridge Management System (BMS), strengthen management of bridge safety inspection by expanding national participation, Organization and operation of bridge safety maintenance budget, concentration management of deteriorated bridge and long span bridge etc. In future the establishment of bridges life-cycle management system (LCM) to a preventive maintenance system by means of record management comparing with life-cycle costs (LCC) should be implemented to the comprehensive overall maintenance system of mid to long-term budget formulation and execution by applying professional and active citizen participation procedures. -

Compensating Victims of Bridge Collapses Outside Minnesota
Compensating Victims of Bridge Collapses Outside Minnesota Peter S. Wattson Senate Counsel State of Minnesota November 9, 2007 2 Contents Introduction ................................................................ ii 1. Tacoma Narrows Bridge - Washington - November 7, 1940 ....................1 2. Silver Bridge - West Virginia - December 15, 1967 ...........................2 3. Mianus River Bridge - Connecticut - June 28, 1983 ...........................3 4. Schoharie Creek Bridge - New York - April 5, 1987 ..........................4 5. Hatchie River Bridge - Tennessee - April 1, 1989 .............................6 6. San Francisco-Oakland Bay Bridge and Cypress Structure - California - October 17, 1989 ...............................................................7 7. Little Red River Pedestrian Bridge - Arkansas - October 29, 1989 ..............9 8. I-40 Bridge Near Webbers Falls - Oklahoma - May 26, 2002 ..................10 Conclusion .................................................................11 Bridge Collapse Web Sites ....................................................12 i Introduction This paper describes how other states have compensated victims of bridge collapses that occurred before the Interstate 35W Bridge over the Mississippi River in Minneapolis collapsed on August 1, 2007. It includes bridges that collapsed in California, Connecticut, New York, Oklahoma, Tennessee, Washington, and West Virginia, from 1940 to 2002. The collapses and the state response to them are described in chronological order. They offer an -

Jeffery Harvey: Bridge Collapse Reminds Us to Have Emergency Plans
Jeffery Harvey: Bridge collapse reminds us to have emergency plans... http://www.herald-dispatch.com/opinion/jeffery-harvey-bridge-col... http://www.herald-dispatch.com/opinion/jeffery-harvey-bridge-collapse-reminds-us-to-have-emergency- plans/article_6d68e5f3-5d46-5f9d-95bf-0db189d13558.html Jeffery Harvey: Bridge collapse reminds us to have emergency plans 11 hrs ago Bo Wriston Buy Now This December, West Virginians and Ohioans are reminded of one disaster that no one could have predicted. This month marks the 50th anniversary of the Silver Bridge Collapse, which sparked mass public attention and major concerns for bridge safety across the country. More than that, it took many American lives in the blink of an eye, and those that were spared and witnessed the event will forever be haunted by what they experienced that day. On that Dec. 15 in 1967, around 5 p.m., the Silver Bridge was full of rush-hour traffic that flowed between Point Pleasant, West Virginia, and Gallipolis, Ohio. Many were probably expecting to drive across that bridge like they had done so many times before, perhaps with work still on their minds or pondering what to fix for dinner that night. Yet, something happened that no one expected. The 1 of 3 12/15/17, 1:44 PM Jeffery Harvey: Bridge collapse reminds us to have emergency plans... http://www.herald-dispatch.com/opinion/jeffery-harvey-bridge-col... bridge's infrastructure gave out; the innovative eyebar-link suspension of the time had failed. In less than a minute, witnesses said the bridge crumbled and sank into the Ohio River, taking 37 vehicles and the lives of 46 people with it. -

The Persistence of Failure Historic Bridge Collapses
The Persistence of Failure Historic Bridge Collapses Henry Petroski Distinguished Professor Emeritus of Civil Engineering Duke University • • • Historic Failures of Iron and Steel Bridges • What are the Landmark Cases? • Do They Reveal a Pattern? • Can It Predict Future Collapses? Landmark Bridge Failures (some still being revisited) North British Railway, Edinburgh-to-Dund ee, ca. late 1870 Chester and Holyhead Railway, Ca. 1845 Dee Bridge Collapse 1847 Collapsed Dee Bridge Trussed Girder Revisiting the Dee Bridge Failure Peter Lewis, Open University, ca. 2004 Tay Bridge Collapse 1879 Tay Bridge, 1879 Tay Bridge, 1879 Dec. 28, 1879 Note smokestacks still standing in Dundee. In 2002 Peter Lewis digitized 1880 photos Replacement Tay Bridge (left), 1887 Bridge Proposed to Cross the Firth of Forth (Design Abandoned after Tay Bridge Collapse) Forth Railway Bridge Human Model, late 1880s Forth Rail Bridge, 1890 Quebec Bridge Collapse 1907 Quebec Bridge, 1907 (Second) Quebec Bridge, 1917 Tacoma Narrows Bridge Collapse 1940 Tacoma Narrows Bridge, 1940 Tacoma Narrows Bridge, 1940 Silver Bridge Collapse 1967 Silver Bridge, 1928 Silver Bridge Collapse December 15, 1967 Milford Haven Bridge Collapse 1970 Milford Haven Bridge June 1970 Cleddau (Milford Haven) Bridge,1975 Westgate Bridge October 1970 367-foot span being lifted onto piers Landmark Bridge Failures Is there a pattern? • 1847 - Dee Bridge, trussed girder • 1879 - Tay Bridge, through truss • 1907 - Quebec Bridge, cantilever • 1940 - Tacoma Narrows Bridge, suspension • 1967 - Silver -
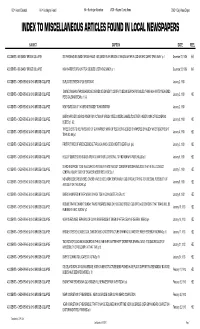
Copy of Huntington History Index 6-7-10.Xlsx
HD = Herald Dispatch HH = Huntington Herald HA = Huntington Advertiser WCN = Wayne County News DND = Daily News Digest INDEX TO MISCELLANEOUS ARTICLES FOUND IN LOCAL NEWSPAPERS SUBJECT CAPTION DATE REEL ACCIDENTS - BIG SANDY BRIDGE COLLAPSE SIX PERISH AS BIG SANDY BRIDGE FALLS : BIG SANDY RIVER BRIDGE AT KENOVA AFTER FLOOD WATERS CARRY SPAN AWAY p. 1 December 22, 1926 HA ACCIDENTS - BIG SANDY BRIDGE COLLAPSE HIGH WATER STOPS HUNT FOR 5 BODIES LOST IN BIG SANDY p. 1 December 23, 1926 HA ACCIDENTS - CHESAPEAKE & OHIO BRIDGE COLLAPSE DUPLICATES WRECK OF 20 YEARS AGO January 2, 1913 ENGINE CRASHING THROUGH BRIDGE CARRIES SEVEN MEN TO DEATH; TO BEGIN SEARCH FOR BODIES: THINK HIGH WATER WEAKENED ACCIDENTS - CHESAPEAKE & OHIO BRIDGE COLLAPSE January 2, 1913 HD PIERS CAUSING BREAK p. 1 & 3 ACCIDENTS - CHESAPEAKE & OHIO BRIDGE COLLAPSE NEW YEARS DAY OF 1913 BRING TRAGEDY TO HUNTINGTON January 2, 1913 DIVERS ARRIVE TO SEARCH RIVER FOR VICTIMS OF WRECK: STEEL GIRDERS JAMMED TOGETHER, HINDER WORK OF RECOVERING ACCIDENTS - CHESAPEAKE & OHIO BRIDGE COLLAPSE January 3, 1913 HD BODIES p.1 & 2 THREE DIVERS TO HELP IN SEARCH OF GUYAN RIVER: WORK OF RECOVERING BODIES IS HAMPERED BY MUDDY WATER [C&O FREIGHT ACCIDENTS - CHESAPEAKE & OHIO BRIDGE COLLAPSE January 4, 1913 HD TRAIN NO. 99] p.1 ACCIDENTS - CHESAPEAKE & OHIO BRIDGE COLLAPSE FIRST PICTURES OF WRECKED BRIDGE THROUGH WHICH SEVEN WENT TO DEATH p.6 (pic) January 5, 1913 HD ACCIDENTS - CHESAPEAKE & OHIO BRIDGE COLLAPSE HELD BY DEBRIS SEVEN BODIES ARE IN GUYAN RIVER...DIVERS FAIL TO FIND MEN WHO WERE