The Hot Hand and Its Effect on The
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Probable Starters
UTAH JAZZ (35-30) at MEMPHIS GRIZZLIES (18-46) Game #66 • ROAD Game #34 • FedExForum • MEMPHIS March 9, 2018 • 6 p.m. (MT) • TV: AT&T SportsNet RADIO: 1280 AM/97.5 FM DATE OPP. TIME (MT) RECORD/TV 10/18 DEN W, 106-96 1-0 10/20 @MIN L, 97-100 1-1 LAST GAME’S STARTERS (2017-18 averages) 10/21 OKC W, 96-87 2-1 10/24 @LAC L, 84-102 2-2 • Notched first career double-double (11 points, 10/25 @PHX L, 88-97 2-3 career-high 10 assists) at IND on 3/7 10/28 LAL W, 96-81 3-3 PPG • 10.9 10/30 DAL W, 104-89 4-3 2 • Second in the league in three-point 11/1 POR W, 112-103 (OT) 5-3 RPG • 4.1 percentage (.445) 11/3 TOR L, 100-109 5-4 JOE INGLES • Has eight games this season with 5+ 3FG 11/5 @HOU L, 110-137 5-5 11/7 PHI L, 97-104 5-6 F • 6-8 • 226 • Australia APG • 4.3 • Appeared in his 200th straight game on 2/24 11/10 MIA L, 74-84 5-7 vs. DAL 11/11 BKN W, 114-106 6-7 11/13 MIN L, 98-109 6-8 • Has made a three-pointer in consecutive 11/15 @NYK L, 101-106 6-9 PPG • 12.2 games for just the second time in his career 11/17 @BKN L, 107-118 6-10 15 11/18 @ORL W, 125-85 7-10 RPG • 7.4 • Ranks seventh in Jazz history in blocked shots 11/20 @PHI L, 86-107 7-11 DERRICK FAVORS (641) 11/22 CHI W, 110-80 8-11 Jazz are 11-3 when he records a double- 11/25 MIL W, 121-108 9-11 • APG • 1.3 11/28 DEN W, 106-77 10-11 F • 6-10 • 265 • Georgia Tech double 11/30 @LAC W, 126-107 11-11 st 12/1 NOP W, 114-108 12-11 • Posted his 21 double-double of the season 12/4 WAS W, 116-69 13-11 27 PPG • 13.6 (23 points and 14 rebounds) at IND (3/7) 12/5 @OKC L, 94-100 13-12 • Made a career-high 12 free throws and scored 12/7 HOU L, 101-112 13-13 RPG • 10.5 12/9 @MIL L, 100-117 13-14 RUDY GOBERT a season-high 26 points vs. -

Chuckers: Measuring Lineup Shot Distribution Optimality Using Spatial Allocative Efficiency Models
Chuckers: Measuring Lineup Shot Distribution Optimality Using Spatial Allocative Efficiency Models Nathan Sandholtz1 Jacob Mortensen1 Luke Bornn1,2 [email protected] [email protected] [email protected] 1. Introduction In the 2017-18 NBA playoffs, Russell Westbrook scored 46 points on 43 shot attempts in a 96-91 loss to the Utah Jazz, ending the Oklahoma City Thunder's season. At the time, many popular media figures conjectured that having one player dominate field goal attempts in this way would limit the Thunder's success. While scoring 46 points in a playoff basketball game is an impressive feat for any one player, its impact on the win column is moderated by the fact that it required 43 attempts. At its core, this critique is about efficiency. Modern discussion around efficiency in the NBA typically focuses on either individual player efficiency or shot selection. Conceptually, the foundation for shot selection efficiency is simple: shots at the rim and 3-point shots have the highest eXpected points per shot, so teams should prioritize these high-value shots. The idea underlying individual player efficiency is also straightforward; scoring more points on the same number of shot attempts increases a team’s chances of winning. However, implicit in any discussion of player efficiency is the idea that inefficient players have a negative impact because basketball is a team sport. We are concerned with efficiency not just because a given player is inefficient, but because inefficient players take shot opportunities away from teammates that may have higher value. In other words, if Westbrook was surrounded by dismal shooters his 43 shot attempts might appear more defensible, but if his inordinate number of attempts prevented highly efficient shots from other players, then he has caused shots to be inefficiently distributed among the players on the team and decreased their winning potential. -

Hawks' Trio Headlines Reserves for 2015 Nba All
HAWKS’ TRIO HEADLINES RESERVES FOR 2015 NBA ALL-STAR GAME -- Duncan Earns 15 th Selection, Tied for Third Most in All-Star History -- NEW YORK, Jan. 29, 2015 – Three members of the Eastern Conference-leading Atlanta Hawks -- Al Horford , Paul Millsap and Jeff Teague -- headline the list of 14 players selected by the coaches as reserves for the 2015 NBA All-Star Game, the NBA announced today. Klay Thompson of the Golden State Warriors earned his first All-Star selection, joining teammate and starter Stephen Curry to give the Western Conference-leading Warriors two All-Stars for the first time since Chris Mullin and Tim Hardaway in 1993. The 64 th NBA All-Star Game will tip off Sunday, Feb. 15, at Madison Square Garden in New York City. The game will be seen by fans in 215 countries and territories and will be heard in 47 languages. TNT will televise the All-Star Game for the 13th consecutive year, marking Turner Sports' 30 th year of NBA All- Star coverage. The Hawks’ trio is joined in the East by Dwyane Wade and Chris Bosh of the Miami Heat, the Chicago Bulls’ Jimmy Butler and the Cleveland Cavaliers’ Kyrie Irving . This is the 11 th consecutive All-Star selection for Wade and the 10 th straight nod for Bosh, who becomes only the third player in NBA history to earn five trips to the All-Star Game with two different teams (Kareem Abdul-Jabbar, Kevin Garnett). Butler, who leads the NBA in minutes (39.5 per game) and has raised his scoring average from 13.1 points in 2013-14 to 20.1 points this season, makes his first All-Star appearance. -

NBA Feature Story
2018-19 NBA Season Already a Wild One By: Isaac Tomoletz On Tuesday, October 16, 2018, the NBA regular season officially started. Before the season started, there were some big moves by players and teams in this past offseason. Starting with the back-to-back Champions, the Golden State Warriors added a big time player to their already stacked team, Demarcus Cousins, who missed the majority of the season with a torn achilles. Another big shocking move was made by two teams, the Toronto Raptors traded star player Demar Derozan for San Antonio Spurs’ Kawhi Leonard. There were also players such as Jimmy Butler of the Minnesota Timberwolves, who wasn’t happy with his current relationship with his team. So many rumors spread about where he’s going. All of these plus other deals and trades such as Carmelo Anthony signing to the Houston Rockets, one of the biggest deals over the summer was former Cavs forward LeBron James signing to the Los Angeles Lakers have fans wondering about the coming season. All of these changes in teams were months ago, but the NBA season is now underway and we have already seen some interesting things. One of the big talks lately has been about the game played on this past Saturday between the Houston Rockets and the Los Angeles Lakers. During the fourth quarter between the two, a foul occured on Brandon Ingram, a player on the Lakers. After the foul, Ingram pushed Rockets guard, James Harden, which resulted in him getting a technical foul. As the situation was being handled, Rajon Rondo of the Lakers and Chris Paul of the Rockets started arguing and then all hell broke loose in the Staples Center in Los Angeles when Rondo threw a punch at Chris Paul and then Ingram hopped in and threw a punch as well. -
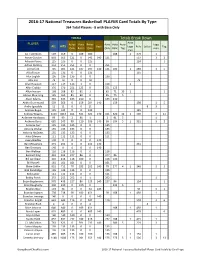
2016-17 National Treasures Basketball PLAYER Card Totals by Type 364 Total Players - 8 with Base Only
2016-17 National Treasures Basketball PLAYER Card Totals By Type 364 Total Players - 8 with Base Only TOTALS Totals Break Down Auto PLAYER Autos Auto Relics Auto Auto Auto Logo ALL HITS Base Logo Relic Letter Tag Only Relics Only Only Relic Tag man man A.J. Hammons 569 569 0 189 380 188 1 379 1 Aaron Gordon 803 663 121 0 542 140 121 537 3 2 Adreian Payne 125 125 0 0 125 124 1 Adrian Dantley 251 251 251 0 0 251 Al Horford 745 605 121 187 297 140 121 186 1 289 3 5 Al Jefferson 135 135 0 0 135 135 Alex English 136 136 136 0 0 136 Alex Len 79 79 0 0 79 79 Allan Houston 117 117 116 1 0 116 1 Allen Crabbe 376 376 251 125 0 251 125 Allen Iverson 168 168 85 82 1 85 71 10 1 1 Alonzo Mourning 165 165 85 80 0 85 75 5 Alvan Adams 345 345 135 210 0 135 210 Andre Drummond 503 363 0 159 204 140 159 198 1 5 Andre Iguodala 11 11 0 0 11 8 3 Andrew Bogut 135 135 0 0 135 135 Andrew Wiggins 1153 1013 161 331 521 140 161 320 10 1 507 3 11 Anfernee Hardaway 99 99 2 96 1 2 91 5 1 Anthony Davis 685 545 99 110 336 140 99 104 5 1 331 3 2 Antoine Carr 135 135 135 0 0 135 Antoine Walker 135 135 135 0 0 135 Antonio McDyess 135 135 135 0 0 135 Artis Gilmore 111 111 111 0 0 111 Avery Bradley 140 0 0 0 0 140 Ben McLemore 371 231 0 0 231 140 231 Ben Simmons 140 0 0 0 0 140 Ben Wallace 116 116 116 0 0 116 Bernard King 333 333 247 86 0 247 86 Bill Laimbeer 216 216 116 100 0 116 100 Bill Russell 161 161 161 0 0 161 Blake Griffin 852 712 78 282 352 140 78 277 4 1 346 3 3 Bob Dandridge 135 135 135 0 0 135 Bob Lanier 111 111 111 0 0 111 Bobby Portis 253 253 252 0 1 252 1 Bojan Bogdanovic 578 438 227 86 125 140 227 86 124 1 Brad Daugherty 230 230 0 230 0 225 5 Bradley Beal 174 34 0 0 34 140 30 3 1 Brandon Ingram 738 738 98 189 451 98 188 1 450 1 Brandon Jennings 140 0 0 0 0 140 Brandon Knight 643 643 116 0 527 116 518 3 6 Brandon Rush 4 4 0 0 4 4 Brice Johnson 640 640 0 189 451 188 1 450 1 Brook Lopez 625 485 0 0 485 140 479 6 Bryn Forbes 140 140 140 0 0 140 Buddy Hield 837 837 232 189 416 232 188 1 415 1 C.J. -

NBA Players Word Search
Name: Date: Class: Teacher: NBA Players Word Search CRMONT A ELLISIS A I A HTHOM A S XTGQDWIGHTHOW A RDIBZWLMVG VKEVINDUR A NTBL A KEGRIFFIN YQMJVURVDE A NDREJORD A NNTX CEQBMRRGBHPK A WHILEON A RDB TFJGOUTO A I A SDIRKNOWITZKI IGPOUSBIIYUDPKEVINLOVEXC MKHVSSTDOKL A YTHOMPSONXJF DMDDEESWLEMMP A ULGEORGEEK U A E A MLBYEMIISTEPHENCURRY NNRVJLW A BYL A ODLVIWJVHLER CUOI A WLNRKLNO A LHORFORDMI A GNDMEWEOESLVUBPZK A LSUYE NIWWESNWNG A IKTIMDUNC A NLI KNIESTR A JEPLU A QZPHESRJIR GOLSHBQD A K A LFKYLELOWRYNV HBLT A RDEMWR A ZSERGEIB A K A I DIIYROGDEM A RDEROZ A NGSJBN ZL A HDOKUSLGDCHRISP A ULUXG OIMSEKL A M A RCUS A LDRIDGEDZ VKSWNQXIDR A YMONDGREENYFZ TONYP A RKER A LECHRISBOSH A P AL HORFORD DWYANE WADE ISAIAH THOMAS DEMAR DEROZAN RUSSELL WESTBROOK TIM DUNCAN DAMIAN LILLARD PAUL GEORGE DRAYMOND GREEN LEBRON JAMES KLAY THOMPSON BLAKE GRIFFIN KYLE LOWRY LAMARCUS ALDRIDGE SERGE IBAKA KYRIE IRVING STEPHEN CURRY KEVIN LOVE DWIGHT HOWARD CHRIS BOSH TONY PARKER DEANDRE JORDAN DERON WILLIAMS JOSE BAREA MONTA ELLIS TIM DUNCAN KEVIN DURANT JAMES HARDEN JEREMY LIN KAWHI LEONARD DAVID WEST CHRIS PAUL MANU GINOBILI PAUL MILLSAP DIRK NOWITZKI Free Printable Word Seach www.AllFreePrintable.com Name: Date: Class: Teacher: NBA Players Word Search CRMONT A ELLISIS A I A HTHOM A S XTGQDWIGHTHOW A RDIBZWLMVG VKEVINDUR A NTBL A KEGRIFFIN YQMJVURVDE A NDREJORD A NNTX CEQBMRRGBHPK A WHILEON A RDB TFJGOUTO A I A SDIRKNOWITZKI IGPOUSBIIYUDPKEVINLOVEXC MKHVSSTDOKL A YTHOMPSONXJF DMDDEESWLEMMP A ULGEORGEEK U A E A MLBYEMIISTEPHENCURRY NNRVJLW A BYL A ODLVIWJVHLER -

Chimezie Metu Demar Derozan Taj Gibson Nikola Vucevic
DeMar Chimezie DeRozan Metu Nikola Taj Vucevic Gibson Photo courtesy of Fernando Medina/Orlando Magic 2019-2020 • 179 • USC BASKETBALL USC • In The Pros All-Time The list below includes all former USC players who had careers in the National Basketball League (1937-49), the American Basketball Associa- tion (1966-76) and the National Basketball Association (1950-present). Dewayne Dedmon PLAYER PROFESSIONAL TEAMS SEASONS Dan Anderson Portland .............................................1975-76 Dwight Anderson New York ................................................1983 San Diego ..............................................1984 John Block Los Angeles Lakers ................................1967 San Diego .........................................1968-71 Milwaukee ..............................................1972 Philadelphia ............................................1973 Kansas City-Omaha ..........................1973-74 New Orleans ..........................................1975 Chicago .............................................1975-76 David Bluthenthal Sacramento Kings ..................................2005 Mack Calvin Los Angeles (ABA) .................................1970 Florida (ABA) ....................................1971-72 Carolina (ABA) ..................................1973-74 Denver (ABA) .........................................1975 Virginia (ABA) .........................................1976 Los Angeles Lakers ................................1977 San Antonio ............................................1977 Denver ...............................................1977-78 -

Charlotte Bobcats
__________________________________________________________________________ __________________________________________________________________________ ALEX STEFANESCU TABLE OF CONTENTS • Awards & Certificates o SIFE Service Leadership Award o PRSSA Certificate of Membership • Charlotte Bobcats o News releases o Other items • CarolinaNightlife.com o News releases o Blog entries • Student Niner Media o Articles & Blog entries • Miscellaneous Items o SIFE Recruitment Flyer AWARDS & CERTIFICATES BOBCATS SPORTS & ENTERTAINMENT, MOBILITIE ANNOUNCE PARTNERSHIP December 21, 2011 – Bobcats Sports & Entertainment President & COO Fred Whitfield announced today the organization has started a partnership with telecommunications infrastructure company, Mobilitie. “We are delighted about our new partnership with Mobilitie,” said Whitfield. “We continually strive to make the fan experience at Time Warner Cable Arena the best in the business and Mobilitie will help us achieve that.” Under the terms of the partnership Mobilitie will provide Distributed Antenna Systems (DAS) that will enhance cellular coverage inside Time Warner Cable Arena. Visitors will have stronger signal, better cell phone reception and fewer dropped calls. The distributed architecture of indoor DAS ensures that customers get wireless coverage inside buildings, in underground train stations and in all other types of indoor environments that traditionally have poor wireless coverage. About Mobilitie: Mobilitie vision is to be the premier owner/investor and lessor of capital assets to -
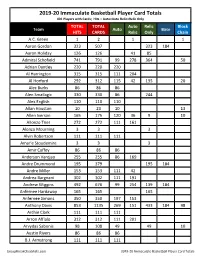
2019-20 Immaculate Basketball Checklist
2019-20 Immaculate Basketball Player Card Totals 401 Players with Cards; Hits = Auto+Auto Relic+Relic Only TOTAL TOTAL Auto Relic Block Team Auto Base HITS CARDS Relic Only Chain A.C. Green 1 2 1 1 Aaron Gordon 323 507 323 184 Aaron Holiday 126 126 41 85 Admiral Schofield 741 791 99 278 364 50 Adrian Dantley 220 220 220 Al Harrington 315 315 111 204 Al Horford 292 312 115 42 135 20 Alec Burks 86 86 86 Alen Smailagic 330 330 86 244 Alex English 110 110 110 Allan Houston 10 23 10 13 Allen Iverson 165 175 120 36 9 10 Allonzo Trier 272 272 111 161 Alonzo Mourning 3 3 3 Alvin Robertson 111 111 111 Amar'e Stoudemire 3 3 3 Amir Coffey 86 86 86 Anderson Varejao 255 255 86 169 Andre Drummond 195 379 195 184 Andre Miller 153 153 111 42 Andrea Bargnani 302 302 111 191 Andrew Wiggins 492 676 99 254 139 184 Anfernee Hardaway 165 165 165 Anfernee Simons 350 350 197 153 Anthony Davis 853 1135 269 151 433 184 98 Archie Clark 111 111 111 Arron Afflalo 312 312 111 201 Arvydas Sabonis 98 108 49 49 10 Austin Rivers 86 86 86 B.J. Armstrong 111 111 111 GroupBreakChecklists.com 2019-20 Immaculate Basketball Player Card Totals TOTAL TOTAL Auto Relic Block Team Auto Base HITS CARDS Relic Only Chain Bam Adebayo 163 347 163 184 Baron Davis 98 118 98 20 Ben Simmons 206 390 5 201 184 Bernard King 230 233 230 3 Bill Laimbeer 4 4 4 Bill Russell 104 117 104 13 Bill Walton 35 48 35 13 Blake Griffin 318 502 5 313 184 Bob McAdoo 49 59 49 10 Boban Marjanovic 264 264 111 153 Bogdan Bogdanovic 184 190 141 42 1 6 Bojan Bogdanovic 247 431 247 184 Bol Bol 719 768 99 287 333 -

Chick-Fil-A Classic Individual Game Tournament Records
Chick-fil-A Classic Individual Game Tournament Records 30 Point Performances Rebounds* 43 Tevin Mack, Dreher 12.19.14 20 Alandre Davis, Wilson 12.22.11 40 Sam Perry, Woodmont 12.19.03 20 Thon Maker, Carlisle 12.23.13 40 Rysheed Jordan, Roberts Vaux 12.22.12 19 Victor Enoh, Greenforest Christian 12.22.14 39 Braxton Ogbueze, United Faith 12.21.11 18 Vernon Macklin, I.C. Norcom 12.20.04 38 Mike Jones, Lower Richland 12.20.04 18 Therrell Gosier, Blanche Ely 12.23.13 37 Richard Hendrix, Athens 12.20.03 17 Lucas Hargrove, Richland Northeast 12.20.05 36 Ahmed Hill, Aquinas 12.21.13 16 Mason Plumlee, Christ School 12.22.08 36 Antwan Holmes, Keenan 12.22.14 16 Isaiah Austin, Grace Prep 12.23.10 35 Randolph Morris, Landmark Christian 12.21.02 16 Donovan Gilmore, Wesleyan Christian 12.23.13 34 Richard Hendrix, Athens 12.22.03 16 Tulio Da Silva, Arlington Country Day 12.20.14 33 Sam Perry, Woodmont 12.22.03 15 Mike Jones, Lower Richland 12.20.04 33 Mike Jones, Lower Richland 12.22.05 15 Benjamin Finney, I.C. Norcom 12.21.04 33 Will Weeks, Christ School 12.22.11 15 Mario Thomas, Lancaster 12.22.05 33 Jared Richardson, Lower Richland 12.23.14 15 Naqui Darby, C.A. Johnson 12.22.08 32 Zam Fredrick, Jr., Calhoun County 12.21.02 15 Keith Clanton, Orlando Christian 12.22.08 32 Devan Downey, Chester 12.21.04 15 Keith Clanton, Orlando Christian 12.20.08 32 Ryan Steed, Pinewood Prep 12.22.06 15 Odell Turner, Myers Park 12.22.08 32 Terrico White, Craigmont 12.21.07 15 Anthony Gill, Charlotte Christian 12.21.09 32 Ryan Kelly, Ravenscroft 12.22.08 15 Grant Jerrett, La Verne Lutheran 12.20.11 32 Jordan Price, Southwest DeKalb 12.20.11 15 Donovan Gilmore, Wesleyan Christian 12.21.13 32 Tevin Mack, Dreher 12.23.14 Jerell Jamison, Brookland-Cayce 12.19.02 31 Blocked Shots* 31 Sam Perry, Woodmont 12.20.03 11 Isaiah Austin, Grace Prep 12.22.10 31 Aaron Branham, East Ridge 12.21.04 10 Ty Walker, New Hanover 12.21.07 31 Daniel Bailey, Hammond 12.22.06 9 Jeff Withey, Horizon 12.21.06 31 Tre Smith, Hillcrest 12.19.12 8 Francis Aihe, Winter Park 12.22.05 31 Rion Davis, A.C. -

PDF Numbers and Names
CeLoMiManca Checklist NBA 2018/2019 - Sticker & Card Collection 1 Oct. 28, 2017 - 17 - Jersey Away Jefferson 70 Jeremy Lamb Russell Westbrook 18 - 36 Kyrie Irving 54 Spencer Dinwiddie 71 Frank Kaminsky 2 Dec. 18, 2017 - Kobe 19 - 37 Jaylen Brown 55 Caris LeVert 72 James Borrego (head Bryant 20 - 38 Al Horford 56 Rondae Hollis- coach) 3 Lauri Markkanen Jefferson 21 - 39 Team Logo 73 Nicolas Batum 4 Jan. 30, 2018 - James 57 Shabazz Napier 22 a - Jersey Home / b - 40 Jason Tatum 74 a - Jersey Home / b - Harden Jersey Away 41 Gordon Hayward 58 Allen Crabbe Jersey Away 5 Feb. 15, 2018 - Nikola 23 Kent Bazemore 42 Marcus Morris 59 Kenny Atkinson 75 Robin Lopez Jokic (head coach) 24 Jeremy Lin 43 Jason Tatum 76 Bobby Portis 6 Feb. 28, 2018 - Dirk 60 D'Angelo Russell 77 Justin Holiday Nowitzki 25 Dewayne Dedmon 44 Terry Rozier 61 a - Jersey Home / b - 26 Team Logo 45 Marcus Smart 78 Team Logo 7 - Jersey Away 27 Taurean Prince 46 Brad Stevens (head 79 Lauri Markkanen 8 - 62 Nicolas Batum 28 De Andrè Bembry coach) 80 Kris Dunn 9 - 63 Tony Parker 29 John Collins 47 Kyrie Irving 81 Denzel Valentine 10 - 64 Cody Zeller 30 Kent Bazemore 48 a - Jersey Home / b - 82 Lauri Markkanen 11 - 65 Team Logo Jersey Away 83 Zach LaVine 12 - 31 Miles Plumlee 49 Jarrett Allen 66 Marvin Williams 32 Tyler Dorsey 84 Jabari Parker 13 - 67 Michael Kidd- 50 DeMarre Carroll 85 Fred Hoiberg (head 14 - 33 Lloyd Pierce (head Gilchrist coach) 51 D'Angelo Russell coach) 15 - 68 Kemba Walker 34 John Collins 52 Team Logo 86 Zach LaVine 16 - 69 Kemba Walker 35 a - Jersey Home -

Player Set Card # Team Print Run Al Horford Top-Notch Autographs
2013-14 Innovation Basketball Player Set Card # Team Print Run Al Horford Top-Notch Autographs 60 Atlanta Hawks 10 Al Horford Top-Notch Autographs Gold 60 Atlanta Hawks 5 DeMarre Carroll Top-Notch Autographs 88 Atlanta Hawks 325 DeMarre Carroll Top-Notch Autographs Gold 88 Atlanta Hawks 25 Dennis Schroder Main Exhibit Signatures Rookies 23 Atlanta Hawks 199 Dennis Schroder Rookie Jumbo Jerseys 25 Atlanta Hawks 199 Dennis Schroder Rookie Jumbo Jerseys Prime 25 Atlanta Hawks 25 Jeff Teague Digs and Sigs 4 Atlanta Hawks 15 Jeff Teague Digs and Sigs Prime 4 Atlanta Hawks 10 Jeff Teague Foundations Ink 56 Atlanta Hawks 10 Jeff Teague Foundations Ink Gold 56 Atlanta Hawks 5 Kevin Willis Game Jerseys Autographs 1 Atlanta Hawks 35 Kevin Willis Game Jerseys Autographs Prime 1 Atlanta Hawks 10 Kevin Willis Top-Notch Autographs 4 Atlanta Hawks 25 Kevin Willis Top-Notch Autographs Gold 4 Atlanta Hawks 10 Kyle Korver Digs and Sigs 10 Atlanta Hawks 15 Kyle Korver Digs and Sigs Prime 10 Atlanta Hawks 10 Kyle Korver Foundations Ink 23 Atlanta Hawks 10 Kyle Korver Foundations Ink Gold 23 Atlanta Hawks 5 Pero Antic Main Exhibit Signatures Rookies 43 Atlanta Hawks 299 Spud Webb Main Exhibit Signatures 2 Atlanta Hawks 75 Steve Smith Game Jerseys Autographs 3 Atlanta Hawks 199 Steve Smith Game Jerseys Autographs Prime 3 Atlanta Hawks 25 Steve Smith Top-Notch Autographs 31 Atlanta Hawks 325 Steve Smith Top-Notch Autographs Gold 31 Atlanta Hawks 25 groupbreakchecklists.com 13/14 Innovation Basketball Player Set Card # Team Print Run Bill Sharman Top-Notch Autographs