The Insignificant Evolution of the Richness-Mass Relation of Galaxy
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The X-Ray Universe 2011
THE X-RAY UNIVERSE 2011 27 - 30 June 2011 Berlin, Germany A conference organised by the XMM-Newton Science Operations Centre, European Space Astronomy Centre (ESAC), European Space Agency (ESA) ABSTRACT BOOK Oral Communications and Posters Edited by Andy Pollock with the help of Matthias Ehle, Cristina Hernandez, Jan-Uwe Ness, Norbert Schartel and Martin Stuhlinger Organising Committees Scientific Organising Committee Giorgio Matt (Universit`adegli Studi Roma Tre, Italy) Chair Norbert Schartel (XMM-Newton SOC, Madrid, ESA) Co-Chair M. Ali Alpar (Sabanci University, Istanbul, Turkey) Didier Barret (Centre d’Etude Spatiale des Rayonnements, Toulouse, France) Ehud Behar (Technion Israel Institute of Technology, Haifa, Israel) Hans B¨ohringer (MPE, Garching, Germany) Graziella Branduardi-Raymont (University College London-MSSL, Dorking, UK) Francisco J. Carrera (Instituto de F´ısicade Cantabria, Santander, Spain) Finn E. Christensen (Danmarks Tekniske Universitet, Copenhagen, Denmark) Anne Decourchelle (Commissariat `al’´energie atomique et aux ´energies alternatives, Saclay, France) Jan-Willem den Herder (SRON, Utrecht, The Netherlands) Rosario Gonzalez-Riestra (XMM-Newton SOC, Madrid, ESA) Coel Hellier (Keele University, UK) Stefanie Komossa (MPE, Garching, Germany) Chryssa Kouveliotou (NASA/Marshall Space Flight Center, Huntsville, Alabama, USA) Kazuo Makishima (University of Tokyo, Japan) Sera Markoff (University of Amsterdam, The Netherlands) Brian McBreen (University College Dublin, Ireland) Brian McNamara (University of Waterloo, Canada) -

Weak Lensing Galaxy Cluster Field Reconstruction
Mon. Not. R. Astron. Soc. 000, 1–12 (2012) Printed 14 October 2018 (MN LATEX style file v2.2) Weak Lensing Galaxy Cluster Field Reconstruction E. Jullo1, S. Pires2, M. Jauzac3 & J.-P. Kneib4;1 1Aix Marseille Université, CNRS, LAM (Laboratoire d’Astrophysique de Marseille) UMR 7326, 13388, Marseille, France 2Laboratoire AIM, CEA/DSM-CNRS, Université Paris 7 Diderot, IRFU/SAp-SEDI, Service d’Astrophysique, CEA Saclay, Orme des Merisiers, 91191 Gif-sur-Yvette, France 3Astrophysics and Cosmology Research Unit, School of Mathematical Sciences, University of KwaZulu-Natal, Durban 4041, South Africa 4LASTRO, Ecole polytechnique fédérale de Lausanne, Suisse Released 2013 Xxxxx XX ABSTRACT In this paper, we compare three methods to reconstruct galaxy cluster density fields with weak lensing data. The first method called FLens integrates an inpainting concept to invert the shear field with possible gaps, and a multi-scale entropy denoising proce- dure to remove the noise contained in the final reconstruction, that arises mostly from the random intrinsic shape of the galaxies. The second and third methods are based on a model of the density field made of a multi-scale grid of radial basis functions. In one case, the model parameters are computed with a linear inversion involving a singular value decomposition. In the other case, the model parameters are estimated using a Bayesian MCMC optimization implemented in the lensing software Lenstool. Methods are compared on simulated data with varying galaxy density fields. We pay particular attention to the errors estimated with resampling. We find the multi-scale grid model optimized with MCMC to provide the best results, but at high computational cost, especially when considering resampling. -

Is the Butcher-Oemler Effect a Function of the Cluster Redshift? S. Andreon
THE ASTROPHYSICAL JOURNAL, 516:647È659, 1999 May 10 ( 1999. The American Astronomical Society. All rights reserved. Printed in U.S.A. IS THE BUTCHER-OEMLER EFFECT A FUNCTION OF THE CLUSTER REDSHIFT? S. ANDREON Osservatorio Astronomico di Capodimonte, via Moiariello 16, 80131 Napoli, Italy; andreon=na.astro.it AND S. ETTORI Institute of Astronomy, Madingley Road, Cambridge CB3 0HA, England, UK; settori=ast.cam.ac.uk Received 1998 May 29; accepted 1998 December 18 ABSTRACT Using PSPC ROSAT data, we measure the X-ray surface brightness proÐles, size, and luminosity of the Butcher-Oemler (BO) sample of clusters of galaxies. The cluster X-ray size, as measured by the Pet- rosianrg/2 radius, does not change with redshift and is independent of X-ray luminosity. On the other hand, the X-ray luminosity increases with redshift. Considering that fair samples show no evolution, or negative luminosity evolution, we conclude that the BO sample is not formed from the same class of objects observed at di†erent look-back times. This is in conÑict with the usual interpretation of the Butcher-Oemler as an evolutionary (or redshift dependent) e†ect, based on the assumption that we are comparing the same class of objects at di†erent redshifts. Other trends present in the BO sample reÑect selection criteria rather than di†erences in look-back time, as independently conÐrmed by the fact that trends lose strength when we enlarge the sample with an X-rayÈselected sample of clusters. The variety of optical sizes and shapes of the clusters in the Butcher-Oemler sample and the Malmquist-like bias are the reasons for these selection e†ects that mimic the trends usually interpreted as changes due to evolu- tion. -

GMRT 610 Mhz Observations of Galaxy Clusters in the ACT Equatorial Sample
MNRAS 000,1{26 (2018) Preprint 20 March 2019 Compiled using MNRAS LATEX style file v3.0 GMRT 610 MHz observations of galaxy clusters in the ACT equatorial sample Kenda Knowles,1? Andrew J. Baker,2 J. Richard Bond,3 Patricio A. Gallardo,4 Neeraj Gupta,5 Matt Hilton,1 John P. Hughes,2 Huib Intema,6 Carlos H. L´opez- Caraballo,7;8 Kavilan Moodley,1 Benjamin L. Schmitt,9 Jonathan Sievers,10 Crist´obal Sif´on,4;11 Edward Wollack,12 1Astrophysics & Cosmology Research Unit, School of Mathematics, Statistics & Computer Science, University of KwaZulu-Natal, Durban, 3690, South Africa 2Department of Physics and Astronomy, Rutgers, The State University of New Jersey, 136 Frelinghuysen Road, Piscataway, NJ 08854-8019, USA 3Canadian Institute for Theoretical Astrophysics, 60 St. George Street, University of Toronto, Toronto, ON, M5S 3H8, Canada 4Department of Physics, Cornell University, Ithaca, NY USA 5IUCAA, Post Bag 4, Ganeshkhind, Pune 411007, India 6Leiden Observatory, Leiden University, PO Box 9513, NL2300 RA Leiden, Netherlands 7Instituto de Astrof´ısica and Centro de Astro-Ingenier´ıa, Facultad de F´ısica, Pontificia Universidad Cat´olica de Chile, Av. Vicu~na Mackenna 4860, 7820436 Macul, Santiago, Chile 8Departamento de Matem´aticas, Universidad de La Serena, Av. Juan Cisternas 1200, La Serena, Chile 9Department of Physics and Astronomy, University of Pennsylvania, 209 South 33rd Street, Philadelphia, PA 19104, USA 10Astrophysics & Cosmology Research Unit, School of Chemistry & Physics, University of KwaZulu-Natal, Durban, 3690, South Africa 11Department of Astrophysical Sciences, Peyton Hall, Princeton University, Princeton, NJ 08544, USA 12NASA/Goddard Space Flight Center, 8800 Greenbelt Rd, Greenbelt, MD 20771, USA Accepted XXX. -

Bibliography of Refereed Papers: Roger L
Bibliography of refereed papers: Roger L. Davies 203 refereed papers, >24,000 citations, h=75 62 papers >100 citations; 13 papers >500 citations and one has more than 1000 citations. [203] Francesco D'Eugenio, Matthew Colless, Nicholas Scott, Arjen van der Wel, Roger L. Davies, Jesse van de Sande, Sarah M. Sweet, Sree Oh, Brent Groves, Rob Sharp, Matt S. Owers, Joss Bland-Hawthorn, Scott M. Croom, Sarah Brough, Julia J. Bryant, Michael Goodwin, Jon S. Lawrence, Nuria P. F. Lorente, and Samuel N. Richards. The SAMI Galaxy Survey: stellar population and structural trends across the Fundamental Plane. MNRAS, April 2021. [202] Scott M. Croom, Matt S. Owers, Nicholas Scott, Henry Poetrodjojo, Brent Groves, Jesse van de Sande, Tania M. Barone, Luca Cortese, Francesco D'Eugenio, Joss Bland-Hawthorn, Julia Bryant, Sree Oh, Sarah Brough, James Agostino, Sarah Casura, Barbara Catinella, Matthew Colless, Gerald Cecil, Roger L. Davies, Michael J. Drinkwater, Simon P. Driver, Ignacio Ferreras, Caroline Foster, Amelia Fraser-McKelvie, Jon Lawrence, Sarah K. Leslie, Jochen Liske, Angel´ R. L´opez-S´anchez, Nuria P. F. Lorente, Rebecca McElroy, Anne M. Medling, Danail Obreschkow, Samuel N. Richards, Rob Sharp, Sarah M. Sweet, Dan S. Taranu, Edward N. Taylor, Edoardo Tescari, Adam D. Thomas, James Tocknell, and Sam P. Vaughan. The SAMI Galaxy Survey: the third and final data release. MNRAS, February 2021. [201] Romina Ahumada and others. The 16th Data Release of the Sloan Digital Sky Surveys: First Release from the APOGEE-2 Southern Survey and Full Release of eBOSS Spectra. ApJS, 249(1):3, July 2020. [200] S. -

16Th HEAD Meeting Session Table of Contents
16th HEAD Meeting Sun Valley, Idaho – August, 2017 Meeting Abstracts Session Table of Contents 99 – Public Talk - Revealing the Hidden, High Energy Sun, 204 – Mid-Career Prize Talk - X-ray Winds from Black Rachel Osten Holes, Jon Miller 100 – Solar/Stellar Compact I 205 – ISM & Galaxies 101 – AGN in Dwarf Galaxies 206 – First Results from NICER: X-ray Astrophysics from 102 – High-Energy and Multiwavelength Polarimetry: the International Space Station Current Status and New Frontiers 300 – Black Holes Across the Mass Spectrum 103 – Missions & Instruments Poster Session 301 – The Future of Spectral-Timing of Compact Objects 104 – First Results from NICER: X-ray Astrophysics from 302 – Synergies with the Millihertz Gravitational Wave the International Space Station Poster Session Universe 105 – Galaxy Clusters and Cosmology Poster Session 303 – Dissertation Prize Talk - Stellar Death by Black 106 – AGN Poster Session Hole: How Tidal Disruption Events Unveil the High 107 – ISM & Galaxies Poster Session Energy Universe, Eric Coughlin 108 – Stellar Compact Poster Session 304 – Missions & Instruments 109 – Black Holes, Neutron Stars and ULX Sources Poster 305 – SNR/GRB/Gravitational Waves Session 306 – Cosmic Ray Feedback: From Supernova Remnants 110 – Supernovae and Particle Acceleration Poster Session to Galaxy Clusters 111 – Electromagnetic & Gravitational Transients Poster 307 – Diagnosing Astrophysics of Collisional Plasmas - A Session Joint HEAD/LAD Session 112 – Physics of Hot Plasmas Poster Session 400 – Solar/Stellar Compact II 113 -

Where Are the Missing Baryons in Clusters?
1 Where Are the Missing Baryons in Clusters? Bilhuda Rasheed Adviser: Dr. Neta Bahcall Submitted in partial fulfillment of the requirements for the degree of Bachelor of Arts Department of Astrophysical Sciences Princeton University May 2010 I hereby declare that I am the sole author of this thesis. I authorize Princeton University to lend this thesis to other institutions or individuals for the purpose of scholarly research. Bilhuda Rasheed I further authorize Princeton University to reproduce this thesis by photocopying or by other means, in total or in part, at the request of other institutions or individuals for the purpose of scholarly research. Bilhuda Rasheed Abstract We address previous claims that the baryon fraction in clusters is significantly below the cosmic value of the baryon fraction as determined from WMAP 7-year results. We use X-ray and SZ observations to determine the slope of the gas density profile to R200. This is shallower than the slope of total mass density (NFW) profile. We use the gas density slope to extrapolate the X-ray observations of gas fraction at R500 to the virial radius (R100). The gas fraction increases beyond R500 for all cluster masses. We add the stellar fraction as determined from COSMOS and 2MASS samples, with ICL contributing 10% to the stellar fraction. For massive clusters 14 (M500 ∼ 7 × 10 M ), the baryon fraction reaches the cosmic baryon fraction at Rvir± 20%. Poorer clusters and groups typically reach 75–85% of the cosmic baryon fraction at the virial radius. We compare these results with simulations which take into account gravitational shock-heating, star formation, heating from SNe and AGN, and energy transfer from dark matter. -

MASS and LIGHT of ABELL 370: a STRONG and WEAK LENSING ANALYSIS ABSTRACT We Present a New Gravitational Lens Model of the Hubble
Draft version October 15, 2018 Preprint typeset using LATEX style emulateapj v. 01/23/15 MASS AND LIGHT OF ABELL 370: A STRONG AND WEAK LENSING ANALYSIS V. Strait1, M. Bradacˇ1, A. Hoag1, K.-H. Huang1, T. Treu2, X. Wang2,4, R. Amorin6,7, M. Castellano5, A. Fontana5, B.-C. Lemaux1, E. Merlin5, K.B. Schmidt3, T. Schrabback8, A. Tomczack1, M. Trenti9,10, and B. Vulcani9,11 1Physics Department, University of California, Davis, CA 95616, USA 2Department of Physics and Astronomy, UCLA, Los Angeles, CA, 90095-1547, USA 3Leibniz-Institut f¨urAstrophysik Postdam (AIP), An der Sternwarte 16, 14482 Potsdam, Germany 4Department of Physics, University of California, Santa Barbara, CA, 93106-9530, USA 5INAF - Osservatorio Astronomico di Roma Via Frascati 33 - 00040 Monte Porzio Catone, 00040 Rome, Italy 6Cavendish Laboratory, University of Cambridge, 19 JJ Thomson Avenue, CB3 0HE, Cambridge, UK 7Kavli Institute for Cosmology, University of Cambridge, Madingley Rd., CB3 0HA, Cambridge, UK 8Argelander-Institut f¨urAstronomie, Auf dem H¨ugel71, D-53121 Bonn, Germany 9School of Physics, University of Melbourne, Parkville, Victoria, Australia 10ARC Centre of Excellence fot All Sky Astrophysics in 3 Dimensions (ASTRO 3D) and 11INAF - Astronomical Observatory of Padora, 35122 Padova, Italy Draft version October 15, 2018 ABSTRACT We present a new gravitational lens model of the Hubble Frontier Fields cluster Abell 370 (z = 0:375) using imaging and spectroscopy from Hubble Space Telescope and ground-based spectroscopy. We combine constraints from a catalog of 909 weakly lensed galaxies and 39 multiply-imaged sources comprised of 114 multiple images, including a system of multiply-imaged candidates at z = 7:84 ± 0:02, to obtain a best-fit mass distribution using the cluster lens modeling code Strong and Weak Lensing United. -

List of Reserved Targets Sent to GRANTECAN for the Exploitation of the MEGARA Guaranteed Time at GTC
List of Reserved Targets sent to GRANTECAN for the exploitation of the MEGARA Guaranteed Time at GTC List of Reserved Targets sent to GRANTECAN for the exploitation of the MEGARA Guaranteed Time at GTC List of Reserved Targets sent to GRANTECAN for the exploitation of the MEGARA Guaranteed Time at GTC INDEX 1. MEGADES – MEGARA GALAXY DISKS EVOLUTION SURVEY: S4G .................. 3 2. MEGADES – MEGARA GALAXY DISKS EVOLUTION SURVEY: M33 ............... 11 3. SPECTROSCOPIC STUDY OF COMPACT STELLAR CLUSTERS AND THEIR SURROUNDINGS IN NEARBY GALAXIES ........................................................................ 12 4. THE CHEMICAL COMPOSITION OF PHOTOIONIZED NEBULAE¡ERROR! MARCADOR NO DEFINIDO. 5. CHROMOSPHERIC ACTIVITY AND AGE OF SOLAR ANALOGS IN OPEN CLUSTERS ................................................................ ¡ERROR! MARCADOR NO DEFINIDO. 6. STUDY OF STELLAR POPULATIONS AND GAS PROPERTIES IN STAR FORMING GALAXIES ............................................................................................................ 14 7. DISSECTING Z∼2-3 HEII-EMITTERS: SPECTRAL TEMPLATES FOR THE SOURCES OF THE COSMIC DAWN ................................................................................... 16 8. CHEMODYNAMICS OF METAL-POOR EXTREME EMISSION LINE GALAXIES AT INTERMEDIATE Z ...................................................................................... 18 9. CONSTRAINING WOLF-RAYET STARS IN EXTREMELY METAL-POOR GALAXIES ................................................................................................................................ -
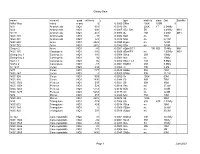
Galaxy Data Name Constell
Galaxy Data name constell. quadvel km/s z type width ly starsDist. Satellite Milky Way many many 0 0.0000 SBbc 106K 200M 0 M31 Andromeda NQ1 -301 -0.0010 SA 220K 1T 2.54Mly M32 Andromeda NQ1 -200 -0.0007 cE2 Sat. 5K 2.49Mly M31 M110 Andromeda NQ1 -241 -0.0008 dE 15K 2.69M M31 NGC 404 Andromeda NQ1 -48 -0.0002 SA0 no 10M NGC 891 Andromeda NQ1 528 0.0018 SAb no 27.3M NGC 680 Aries NQ1 2928 0.0098 E pec no 123M NGC 772 Aries NQ1 2472 0.0082 SAb no 130M Segue 2 Aries NQ1 -40 -0.0001 dSph/GC?. 100 5E5 114Kly MW NGC 185 Cassiopeia NQ1 -185 -0.0006dSph/E3 no 2.05Mly M31 Dwingeloo 1 Cassiopeia NQ1 110 0.0004 SBcd 25K 10Mly Dwingeloo 2 Cassiopeia NQ1 94 0.0003Iam no 10Mly Maffei 1 Cassiopeia NQ1 66 0.0002 S0pec E3 75K 9.8Mly Maffei 2 Cassiopeia NQ1 -17 -0.0001 SABbc 25K 9.8Mly IC 1613 Cetus NQ1 -234 -0.0008Irr 10K 2.4M M77 Cetus NQ1 1177 0.0039 SABd 95K 40M NGC 247 Cetus NQ1 0 0.0000SABd 50K 11.1M NGC 908 Cetus NQ1 1509 0.0050Sc 105K 60M NGC 936 Cetus NQ1 1430 0.0048S0 90K 75M NGC 1023 Perseus NQ1 637 0.0021 S0 90K 36M NGC 1058 Perseus NQ1 529 0.0018 SAc no 27.4M NGC 1263 Perseus NQ1 5753 0.0192SB0 no 250M NGC 1275 Perseus NQ1 5264 0.0175cD no 222M M74 Pisces NQ1 857 0.0029 SAc 75K 30M NGC 488 Pisces NQ1 2272 0.0076Sb 145K 95M M33 Triangulum NQ1 -179 -0.0006 SA 60K 40B 2.73Mly NGC 672 Triangulum NQ1 429 0.0014 SBcd no 16M NGC 784 Triangulum NQ1 0 0.0000 SBdm no 26.6M NGC 925 Triangulum NQ1 553 0.0018 SBdm no 30.3M IC 342 Camelopardalis NQ2 31 0.0001 SABcd 50K 10.7Mly NGC 1560 Camelopardalis NQ2 -36 -0.0001Sacd 35K 10Mly NGC 1569 Camelopardalis NQ2 -104 -0.0003Ibm 5K 11Mly NGC 2366 Camelopardalis NQ2 80 0.0003Ibm 30K 10M NGC 2403 Camelopardalis NQ2 131 0.0004Ibm no 8M NGC 2655 Camelopardalis NQ2 1400 0.0047 SABa no 63M Page 1 2/28/2020 Galaxy Data name constell. -

An ISOCAM Survey Through Gravitationally Lensing Galaxy Clusters
A&A 431, 433–449 (2005) Astronomy DOI: 10.1051/0004-6361:20041782 & c ESO 2005 Astrophysics An ISOCAM survey through gravitationally lensing galaxy clusters IV. Luminous infrared galaxies in Cl 0024+1654 and the dynamical status of clusters D. Coia1, B. McBreen1,L.Metcalfe2,3,A.Biviano4, B. Altieri2,S.Ott5,B.Fort6,J.-P.Kneib7,8, Y. Mellier6,9, M.-A. Miville-Deschênes10 , B. O’Halloran1,11, and C. Sanchez-Fernandez2 1 Department of Experimental Physics, University College, Belfield, Dublin 4, Ireland e-mail: [email protected] 2 XMM-Newton Science Operations Centre, European Space Agency, Villafranca del Castillo, PO Box 50727, 28080 Madrid, Spain 3 ISO Data Centre, European Space Agency, Villafranca del Castillo, PO Box 50727, 28080 Madrid, Spain 4 INAF/Osservatorio Astronomico di Trieste, via G.B. Tiepolo 11, 34131, Trieste, Italy 5 Science Operations and Data Systems Division of ESA, ESTEC, Keplerlaan 1, 2200 AG Noordwijk, The Netherlands 6 Institut d’Astrophysique de Paris, 98 bis boulevard Arago, 75014 Paris, France 7 Observatoire Midi-Pyrénées, 14 avenue Edouard Belin, 31400 Toulouse, France 8 California Institute of Technology, Pasadena, CA 91125, USA 9 Observatoire de Paris, 61 avenue de l’Observatoire, 75014 Paris, France 10 Canadian Institute for Theoretical Astrophysics, 60 St-George Street, Toronto, Ontario M5S 3H8, Canada 11 Dunsink Observatory, Castleknock, Dublin 15, Ireland Received 3 August 2004 / Accepted 26 October 2004 Abstract. Observations of the core of the massive cluster Cl 0024+1654, at a redshift z ∼ 0.39, were obtained with the Infrared Space Observatory using ISOCAM at 6.7 µm (hereafter 7 µm) and 14.3 µm (hereafter 15 µm). -

Epps Seth.Pdf (4.042Mb)
Large-Scale Filaments From Weak Lensing by Seth Epps A thesis presented to the University of Waterloo in fulfillment of the thesis requirement for the degree of Master of Science in Physics Waterloo, Ontario, Canada, 2015 c Seth Epps 2015 I hereby declare that I am the sole author of this thesis. This is a true copy of the thesis, including any required final revisions, as accepted by my examiners. I understand that my thesis may be made electronically available to the public. ii Abstract In the context of non-linear structure formation, a web of dark filaments are expected to intersect the high density regions of the universe, where groups and clusters of galaxies will be forming. In this work we have developed a method for stacking the weak lensing signal of an ensemble of filaments between groups and clusters of galaxies. We detect a the weak lensing signal from stacked filaments between SDSS BOSS luminous red galaxies 13 with the CFHTLenS data at the 5σ level, finding a mass of (1:6 ± 0:3) × 10 M . Two methods of isolating the filament signal are presented: the method of non-physical pair subtraction, and the method of outside region subtraction. This signal is compared with the three-point galaxy-galaxy-convergence correlation function, as developed in Clampitt et al.(2014), yielding reasonably good agreement. iii Acknowledgements I would like to thank my adviser Mike Hudson for his guidance, patience, and contributions. iv Table of Contents List of Figures vii 1 Introduction1 1.1 Structure Formation..............................2 1.1.1 Linear Structure Formation......................2 1.1.2 Non-Linear Structure Formation....................4 1.2 Weak Gravitational Lensing..........................8 1.2.1 Galaxy-Galaxy Lensing........................