Behaviour of Soldier Piles and Timber Lagging Support Systems
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

FITTING-OUT MANUAL for Commercial Occupiers
FITTING-OUT MANUAL for Commercial Occupiers SMRT PROPERTIES SMRT Investments Pte Ltd 251 North Bridge Road Singapore 179102 Tel : 65 6331 1000 Fax : 65 6337 5110 www.smrt.com.sg While every reasonable care has been taken to provide the information in this Fitting-Out Manual, we make no representation whatsoever on the accuracy of the information contained which is subject to change without prior notice. We reserve the right to make amendments to this Fitting-Out Manual from time to time as necessary. We accept no responsibility and/or liability whatsoever for any reliance on the information herein and/or damage howsoever occasioned. 09/2013 (Ver 3.9) Fitting Out Manual SMRT Properties To our Valued Customer, a warm welcome to you! This Fitting-Out Manual is specially prepared for you, our Valued Customer, to provide general guidelines for you, your appointed consultants and contractors when fitting-out your premises at any of our Mass Rapid Transit (MRT) or Light Rail Transit (LRT) stations. This Fitting-Out Manual serves as a guide only. Your proposed plans and works will be subjected to the approval of SMRT and the relevant authorities. We strongly encourage you to read this document before you plan your fitting-out works. Do share this document with your consultants and contractors. While reasonable care has been taken to prepare this Fitting-Out Manual, we reserve the right to amend its contents from time to time without prior notice. If you have any questions, please feel free to approach any of our Management staff. We will be pleased to assist you. -
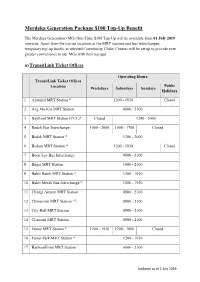
Merdeka Generation Package $100 Top-Up Benefit
Merdeka Generation Package $100 Top-Up Benefit The Merdeka Generation (MG) One-Time $100 Top-Up will be available from 01 July 2019 onwards. Apart from the top-up locations at the MRT stations and bus interchanges, temporary top-up booths at selected Community Clubs/ Centres will be set up to provide even greater convenience to our MGs with their top ups. a) TransitLink Ticket Offices Operating Hours TransitLink Ticket Offices Public Location Weekdays Saturdays Sundays Holidays 1 Aljunied MRT Station * 1200 - 1930 Closed 2 Ang Mo Kio MRT Station 0800 - 2100 3 Bayfront MRT Station (CCL)* Closed 1200 - 2000 4 Bedok Bus Interchange 1000 - 2000 1000 - 1700 Closed 5 Bedok MRT Station * 1200 - 2000 6 Bishan MRT Station * 1200 - 1930 Closed 7 Boon Lay Bus Interchange 0800 - 2100 8 Bugis MRT Station 1000 - 2100 9 Bukit Batok MRT Station * 1200 - 1930 10 Bukit Merah Bus Interchange * 1200 - 1930 11 Changi Airport MRT Station ~ 0800 - 2100 12 Chinatown MRT Station ~@ 0800 - 2100 13 City Hall MRT Station 0900 - 2100 14 Clementi MRT Station 0800 - 2100 15 Eunos MRT Station * 1200 - 1930 1200 - 1800 Closed 16 Farrer Park MRT Station * 1200 - 1930 17 HarbourFront MRT Station ~ 0800 - 2100 Updated as of 2 July 2019 Operating Hours TransitLink Ticket Offices Public Location Weekdays Saturdays Sundays Holidays 18 Hougang MRT Station * 1200 - 1930 19 Jurong East MRT Station * 1200 - 1930 20 Kranji MRT Station * 1230 - 1930 # 1230 - 1930 ## Closed## 21 Lakeside MRT Station * 1200 - 1930 22 Lavender MRT Station * 1200 - 1930 Closed 23 Novena MRT Station -

2014 Student Handbook a Guidebook for Students and Parents
! ! 2014 Student Handbook A guidebook for students and parents ! SSTC_SS_STUDENT_HANDBOOK_20140101_V8.0!©!SSTC!SCHOOL!FOR!FURTHER!EDUCATION!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!0"" ! ! ! 1!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!SSTC_SS_STUDENT_HANDBOOK_20140101_V8.0!©!SSTC!SCHOOL!FOR!FURTHER!EDUCATION" ! CONTENTS INTRODUCTION • A Message from the CEO 3 • A Message from the Principal 4 • Our Vision, Mission, Values and Culture 5 – 6 • School Organisation Chart 7 • Floor Map & Fire Evacuation 8 • Facilities 9 RULES & REGULATIONS • School Rules and Regulations 11 • ICA’s Terms and Conditions of Students’ Pass 12 • Admission/Termination Policy 13 POLICIES & PROCEDURES • Feedback & Complaints 14 – 15 • Transfer/Withdrawal/Deferment Policy & Procedure 16 – 17 • Refund Policy & Procedure 18 – 19 • Academic Honesty Policy 20 • Appeal Policy & Procedure 21 STUDENT SUPPORT & SERVICES • Fee Protection Scheme 22 • Student Support Services 23 – 25 • Reference to CPE’s official website 26 USEFUL INFORMATION • Information for Language Courses 27 • Accounting for Absenteeism 28 • Academic Calendar 2014 29 • Location, Getting there, Amenities & Facilities 30 LIFE IN SINGAPORE • Singapore Laws & Regulations / Singapore Food & Culture 31 • Getting Around in Singapore 32 • Singapore MRT Map 33 • Important / Useful Contacts 34 ! SSTC_SS_STUDENT_HANDBOOK_20140101_V8.0!©!SSTC!SCHOOL!FOR!FURTHER!EDUCATION!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!2"" INTRODUCTION A Message from the CEO We welcome you to SSTC School for Further Education and trust that you will find satisfaction in achieving what you have come to us for; be it preparation for embarking on higher studies, acquiring higher qualifications or learning a new language. We thank you, parents, for choosing us to prepare your children for further education, be it here in Singapore or in other countries abroad. We thank you, mature students, for choosing SSTC to help equip you with Diploma or Degree credentials for a better future. -

Auction & Sales Private Treaty
Auction & Sales Private Treaty. DECEMBER 2019: RESIDENTIAL Salespersons to contact: Tricia Tan, CEA R021904I, 6228 7349 / 9387 9668 Gwen Lim, CEA R027862B, 6228 7331 / 9199 2377 Noelle Tan, CEA R047713G, 6228 7380 / 9766 7797 Teddy Ng, CEA R006630G, 6228 7326 / 9030 4603 Lock Sau Lai, CEA R002919C, 6228 6814 / 9181 1819 Sharon Lee (Head of Auction), CEA R027845B, 6228 6891 / 9686 4449 Ong HuiQi (Admin Support) 6228 7302 Website: http://www.knightfrank.com.sg/auction Email: [email protected] LANDED PROPERTIES FOR SALE * Owner's ** Public Trustee's *** Estate's @ Liquidator's @@ Bailiff's % Receiver's # Mortgagee's ## Developer's ### MCST's Approx. Land / Guide Contact S/no District Street Name Tenure Property Type Room Remarks Floor Area (sqft) Price Person MORTGAGEE SALE One of the best location in Sentosa Cove with a picturesque waterway view. Leasehold 99 2½-Storey Bungalow Noelle / Upside potential. Foreigners are eligible to purchase landed properties only in # 1 D04 PARADISE ISLAND years wef. with Private Pool and 5- 5 7,045 / 8,170 $11.59M Sau Lai / Sentosa Cove. 5 ensuite bedrooms. Efficient layout. Private pool & yacht 07/11/2005 Bedrooms Sharon berth. Vacant possession. More Info MORTGAGEE SALE Leasehold 99 2½-Storey Detached Noelle / Scenic waterway view. Unique façade. Internal lift serving all levels. With # 2 D04 SANDY ISLAND years wef. House with Basement 7 7,307 / 6,727 $11.57M Sau Lai private pool and yacht berth. Basement parking with mechanized parking. 13/06/2007 Parking More Info MORTGAGEE SALE Leasehold 2½-Storey Detached Noelle / Lifestyle living with an enchanting waterway view! 4 ensuite bedrooms. -

Information Memorandum for Mercatus' Multi-Currency Medium
IMPORTANT NOTICE NOT FOR DISTRIBUTION IN THE UNITED STATES OR TO U.S. PERSONS IMPORTANT: You must read the following disclaimer before continuing. The following disclaimer applies to the attached information memorandum. You are advised to read this disclaimer carefully before accessing, reading or making any other use of the attached information memorandum. In accessing the attached information memorandum, you agree to be bound by the following terms and conditions, including any modifications to them from time to time, each time you receive any information from us as a result of such access. Confirmation of Your Representation: In order to be eligible to view the attached information memorandum or make an investment decision with respect to the securities, investors must not be a U.S. person (within the meaning of Regulation S under the Securities Act (as defined below)). The attached information memorandum is being sent at your request and by accepting the e-mail and accessing the attached information memorandum, you shall be deemed to have represented to us (1) that you are not resident in the United States (“U.S.”) nor a U.S. Person, as defined in Regulation S under the U.S. Securities Act of 1933, as amended (the “Securities Act”), nor are you acting on behalf of a U.S. Person, the electronic mail address that you gave us and to which this e-mail has been delivered is not located in the U.S. and, to the extent you purchase the securities described in the attached information memorandum, you will be doing so pursuant to Regulation S under the Securities Act, and (2) that you consent to delivery of the attached information memorandum and any amendments or supplements thereto by electronic transmission. -

Important Notice
IMPORTANT NOTICE NOT FOR DISTRIBUTION IN THE UNITED STATES OR TO U.S. PERSONS IMPORTANT: You must read the following disclaimer before continuing. The following disclaimer applies to the attached information memorandum. You are advised to read this disclaimer carefully before accessing, reading or making any other use of the attached information memorandum. In accessing the attached information memorandum, you agree to be bound by the following terms and conditions, including any modifications to them from time to time, each time you receive any information from us as a result of such access. Confirmation of Your Representation: In order to be eligible to view the attached information memorandum or make an investment decision with respect to the securities, investors must not be a U.S. person (within the meaning of Regulation S under the Securities Act (as defined below)). The attached information memorandum is being sent at your request and by accepting the e-mail and accessing the attached information memorandum, you shall be deemed to have represented to us (1) that you are not resident in the United States (“U.S.”) nor a U.S. Person, as defined in Regulation S under the U.S. Securities Act of 1933, as amended (the “Securities Act”), nor are you acting on behalf of a U.S. Person, the electronic mail address that you gave us and to which this e-mail has been delivered is not located in the U.S. and, to the extent you purchase the securities described in the attached information memorandum, you will be doing so pursuant to Regulation S under the Securities Act, and (2) that you consent to delivery of the attached information memorandum and any amendments or supplements thereto by electronic transmission. -

AFFINITY Floorplanbrochure FA2
H o m e C o m m u n i t y L i fe COME HOME T O ALL THA T Y OU CHERISH A F F I N I T Y Draw nearer to all that matters Located mere minutes across from Serangoon Gardens, AFFINITY is so much more than just a home — it is your key to a charmed life. As neighbour to this beloved heritage estate, soak in its laidback atmosphere reminiscent of times past while never missing out on all of the modern conveniences. From famed hawker fare to hipster eats, old-school provisions to 24-hour groceries, and an international selection of cuisines and schools, Serangoon Gardens has got it all. Welcome to the neighbourhood! Location: Kensington Park Road 01 A F F I N I T Y TAMPINES EXPRESSWAY (TPE) Future Sengkang West S H O P P I N G & D I N I N G E D U C A T I O N Industrial Park P R I M A R Y S C H O O L W I T H I N 1 K M Chomp Chomp Food Centre Seletar Aerospace Park Future Punggol Serangoon Garden Rosyth School Digital District Market & Food Centre Zhonghua Primary School myVillage P R I M A R Y S C H O O L B E T W E E N 1 – 2 K M NEX Mall CHIJ Our Lady of Good Counsel W Serangoon Central Sengkang Xinmin Primary School Upper Serangoon Shopping Centre MRT Station Heartland Mall Hougang Primary School Yio Chu Kang Primary School Kovan Market & Food Centre GO Montfort Junior School* Future Hainanese Village Centre Lorong Halus Xinghua Primary School* ( Ci Yuan Hawker Centre Industrial Park * Hougang Mall Yangzheng Primary School ESSWAY ESSWAY AMK Hub S E C O N D A R Y S C H O O L Jubilee Square Park Connector Network Serangoon Garden Secondary School North East Riverine Loop Access Point Buangkok Bowen Secondary School Yio Chu Kang MRT Station Xinmin Secondary School MRT Station BUANG Montfort Secondary School R EE S P O R T S & R E C R E A T I O N G Paya Lebar Methodist Girls’ Hougang Yio Chu Kang Serangoon Sports & Secondary School Serangoon North Primary School Primary School Punggol Park Recreation Centre Yuying Secondary School Industrial Estate Serangoon Stadium Ci Yuan Hawker Centre Zhonghua Secondary School C Serangoon Public Library St. -

BUS ROUTES in SINGAPORE Route No
BUS ROUTES IN SINGAPORE Route No. Origin Destination 1N Marina Centre Bus Terminal Yishun Ring Road 2♿ Changi Village Bus Terminal New Bridge Road Bus Terminal 2N Marina Centre Bus Terminal Tampines Avenue 3 3♿ Tampines Bus Interchange !unggol Bus Interchange 3A♿ Tampines Bus Interchange !asir Ris Drive 12 3B♿ !asir Ris Drive 1 !asir Ris Bus Interchange 3N Marina Centre Bus Terminal Choa Chu Kang North $ %N Marina Centre Bus Terminal !asir Ris Drive 1 $♿ Bu&it Merah Bus Interchange !asir Ris Bus Interchange $N Marina Centre Bus Terminal 'urong West Street 92 + !asir Ris Bus Interchange ,o-ang Crescent +N Marina Centre Bus Terminal !unggol Field /♿ Bedok Bus Interchange Clementi Bus Interchange 0 Tampines Bus Interchange Toa Payoh Bus Interchange * Bedok Bus Interchange Changi Airport Cargo Comple1 *A Bedok Bus Interchange ,o-ang Avenue 12♿ Tampines Bus Interchange #ent Ridge Bus Terminal 12e Bedok Road )henton Way 11 3e-lang Lorong 1 Bus Terminal National Stadium 12♿ !asir Ris Bus Interchange New Bridge Road Bus Terminal 13♿ 4pper East Coast Bus Terminal Yio Chu Kang Bus Terminal 13A♿ Ang Mo Kio Avenue 6 Bishan Road 1%♿ Clementi Bus Interchange Bedok Bus Interchange 1%A♿ Bedok Bus Interchange 3range Road 1%e Bedok North Avenue 3 6rchard Road Route No. Origin Destination 1$♿ !asir Ris Bus Interchange Marine Parade Road 1$A♿ !asir Ris Bus Interchange 'alan Eunos 1+♿ Bu&it Merah Bus Interchange Bedok Bus Interchange 1/♿ !asir Ris Bus Interchange Bedok Bus Interchange 1/A Bedok Bus Interchange Bedok North Avenue 4 10♿ Tampines Bus Interchange -

Private Treaty List
PRIVATE TREATY LIST SEPTEMBER 2020 RESIDENTIAL LANDED Guide Property Details Contact Person Price 17 CORAL ISLAND, D04 Mortgagee sale: Detached, 2 ½-storey, 4 + 1-bedrooms. Leasehold 99 years wef 2005. VP. $10.x m 1. Joy: 9151 9009 Land / floor area: approx. 7,557 sq ft / 8,697 sq ft, respectively VTO Orientated towards on the waterway, with private yacht berth and swimming pool. 2 PARADISE ISLAND, D04 Mortgagee sale: Detached, 2 ½-storey, 5 + 1-bedrooms. Leasehold 99 years wef 2005. VP. $9.x m 2. Joy: 9151 9009 Land / floor area: approx. 7,045 sq ft / 8,170 sq ft, respectively VTO Orientated towards on the waterway, with private yacht berth and swimming pool. 10 SANDY ISLAND, D04 Mortgagee sale: Detached, 2 ½-storey with basement. Leasehold 99 years wef 2007. VP. 3. $11.x m Joy: 9151 9009 Land / floor area: approx. 7,307 sq ft / 6,727 sq ft, respectively Orientated towards on the waterway, with private yacht berth and swimming pool. LOTUS AVENUE (OFF SIXTH AVENUE), D10 Mortgagee sale: Detached, 2 ½-storey + basement, 5 + 3-bedrooms. Freehold. VP. 4. $9.x m Joy: 9151 9009 Land / floor area: approx. 4,647 sq ft / 8,036 sq ft, respectively Located off prime Sixth Avenue. With swimming pool and internal passenger lift. Huge, spacious layout. LILY AVENUE (OFF SIXTH AVENUE), D10 Owner sale: Detached, 2 ½-storey, 5 + 1-bedrooms. Freehold, sale with existing tenancy. 5. 25 March $8.x m Joy: 9151 9009 Land / floor area: approx. 4,786 sq ft / 5,000 sq ft, respectively Located off prime Sixth Avenue. -

2016 Annual Report and Appendix
Annual Reports and Related Documents:: Page 1 of 1 Annual Reports and Related Documents:: Issuer & Securities Issuer/ Manager CITY DEVELOPMENTS LIMITED Securities CITY DEVELOPMENTS LIMITED - SG1R89002252 - C09 Stapled Security No Announcement Details Announcement Title Annual Reports and Related Documents Date & Time of Broadcast 27-Mar-2017 17:13:33 Status New Report Type Annual Report Announcement Reference SG170327OTHREHNK Submitted By (Co./ Ind. Name) Enid Ling Peek Fong Designation Company Secretary Description (Please provide a detailed description of the event in the box below - Please see attached. Refer to the Online help for the format) Additional Details Period Ended 31/12/2016 Attachments CDL_Annual_Report_2016_.PDF CDL-Appendix.pdf Total size =3393K http://infopub.sgx.com/Apps?A=COW_CorpAnnouncement_Content&B=Announcem... 3/27/2017 CITY DEVELOPMENTS LIMITED ANNUAL REPORT 2016 Building Value Targeting Growth Building Value Targeting Growth Driven by a passion and purpose to ‘Build Value’, we define our success by the value we have created for our stakeholders. Against the backdrop of a rapidly evolving business landscape, we continue to transform our organisational frameworks and develop our growth platforms. Our multi-dimensional focus on innovation and collaboration will be the key drivers of our business success in the new economy. By leveraging our enterprise agility, we will accelerate our strategic diversification objectives for sustained growth – and deliver enhanced value for our stakeholders. OVERVIEW 01 Corporate -

List of Locations Where No Installation of Banners Is Allowed.Xlsx
List of locations where no installation of banners is allowed (Please note that the list is non-exhaustive) S/No. Locations 1 Adam Flyover near Dunearn Close LP49F 2 Adam Flyover near Jln Kembang Melati LP69F 3 Adam Rd aft Adam Park LP34/9 4 Adam Rd bf Adam Dr (exit PIE Changi) LP16 5 Adam Rd bf Sime Rd LP6 6 Adam Rd near Japanese Association LP35 7 Adam Road approaching Dunearn Road LP 37/2 8 Airport Road approaching Eunos Link LP 63 9 Alexandra Rd (Near Malan Rd) LP179 10 Alexandra Rd (Near NOL Building) LP200 11 Alexandra Rd / Depot Rd LP162 12 Alexandra Rd approaching Commonwealth Ave/Leng Kee Bf LP69 13 Alexandra Rd bef Dawson Rd (Centre Median) SP opp LP84 14 Alexandra Rd bet Malan Rd and Hyderabad Rd LP 186 15 Alexandra Rd opp Anchorpoint Shopping Centre LP112-1 16 Alexandra Rd opp Blk101 Henderson Cresent LP21 17 Alexandra Rd opp Cycle & Carriage SP 18 Alexandra Rd opp Pat's School House LP32 19 Alexandra Rd opp Queensway Shopping Centre LP128 20 Alexandra Rd opp Volvo LP77 21 Alexandra Rd/Tanglin Rd/Tiong Bahru Rd (Centre Median) TL8 22 Alexandra Road approaching Pasir Panjang Road / Telok Blangah Road LP 187 23 Aljunied Rd between Sims Ave and Sims Dr LP 8 24 AMK Ave 1 (After AMK St 32) SP 25 AMK Ave 1 (After Marymount Rd) LP70 26 AMK Ave 1 (Outside SPC Petrol Station) LP93 27 AMK Ave 1 / AMK Ave 10 Junction LP136 28 AMK Ave 1 / AMK Ave 2 TL2 29 AMK Ave 1 / AMK Ave 3 TL7 30 AMK Ave 3 / AMK Ave 10 TL5 31 AMK Ave 3 / AMK Ave 4 TL6 32 AMK Ave 3 / AMK St 11 LP17 33 AMK Ave 3 / AMK St 12 TL1 34 AMK Ave 3 / AMK St 42 TL7 35 AMK Ave -

MORTGAGEE SALE Leasehold 99 2½-Storey Detached Scenic Waterway View
Auction & Sales Private Treaty. SEP 2020: RESIDENTIAL Salespersons to contact: Tricia Tan, CEA R021904I, 6228 7349 / 9387 9668 James Wong, CEA R017407Z, 6228 7345 / 9113 3113 Gwen Lim, CEA R027862B, 6228 7331 / 9199 2377 Teddy Ng, CEA R006630G, 6228 7326 / 9030 4603 Noelle Tan, CEA R047713G, 6228 7380 / 9766 7797 Lock Sau Lai, CEA R002919C, 6228 6814 / 9181 1819 Sharon Lee (Head of Auction), CEA R027845B, 6228 6891 / 9686 4449 Ong HuiQi (Admin Support) 6228 7302 LANDED PROPERTIES FOR SALE * Owner's ** Public / Private Trustee's *** Estate's @ Liquidator's @@ Bailiff's % Receiver's # Mortgagee's ## Developer's Approx. Land / Contact S/no District Street Name Tenure Property Type Room Guide Price Remarks Floor Area (sqft) Person MORTGAGEE SALE Leasehold 99 2½-Storey Detached Scenic waterway view. Unique façade. Internal lift serving all Noelle / # 1 D04 SANDY ISLAND years wef. House with Basement 7 7,307 / 6,727 $11.3M levels. With private pool and yacht berth. Basement parking with Sau Lai 13/06/2007 Parking mechanized parking. More Info 3-Storey Cluster 6 bedrooms (all ensuite). Bus services to Sentosa Island and BUKIT TERESA ROAD * 2 D04 Freehold Bungalow with Roof 6 7,567 $3.9M Sau Lai SGH. Near Tiong Bahru and Harbourfront MRT. TERESA VILLAS Garden & Basement More Info Leasehold Ideal for rebuild. Wide frontage of 16.5m. Walking distance to Cold 999 years Land with Single James / * 3 D10 JALAN ISTIMEWA 3,548 $5.5M Storage Jelita, Henry Park Primary School. wef. Storey Semi-Detached Sharon 21/06/1877 Click here for Video Tour 4 Bedrooms (ensuites).