DOCSLIB.ORG

Metric Learning with Rank and Sparsity Constraints

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Metric Learning with Rank and Sparsity Constraints METRIC LEARNING WITH RANK AND SPARSITY CONSTRAINTS Bubacarr Bahy Stephen Becker? Volkan Cevhery Baran Gozc¨ u¨y y Laboratory for Information and Inference Systems, EPFL, Switzerland ? IBM Research, Yorktown Heights, USA ABSTRACT Even though (1) is a convex program, its numerical solution Choosing a distance preserving measure or metric is fun- proves to be challenging since it does not fit into the stan- damental to many signal processing algorithms, such as k- dard convex optimization formulations, such as semidefinite means, nearest neighbor searches, hashing, and compressive or quadratic programming. Moreover, as the number of vari- sensing. In virtually all these applications, the efficiency ables is quadratic with the number of features, even the most of the signal processing algorithm depends on how fast we basic gradient-only approaches do not scale well [1, 4]. can evaluate the learned metric. Moreover, storing the chosen In general, the solution of (1) results in metrics that are metric can create space bottlenecks in high dimensional signal full rank. Hence, the learned metric creates storage as well processing problems. As a result, we consider data dependent as computational bottlenecks. As a result, several works [2, metric learning with rank as well as sparsity constraints. We 3, 5, 6] consider learning rank-constrained metrics. Unfortu- propose a new non-convex algorithm and empirically demon- nately, enforcing rank constraints on the already computation- strate its performance on various datasets; a side benefit is ally challenging MLP (1) makes it non-convex. Surprisingly, that it is also much faster than existing approaches. The under certain conditions, it is possible to prove approxima- added sparsity constraints significantly improve the speed of tion quality and the generalization of solution algorithms in multiplying with the learned metrics without sacrificing their the high-dimensional limit [3, 5]. quality. In this paper, we reformulate the standard MLP (1) into Index Terms— Metric learning, Nesterov acceleration, a non-convex optimization framework that can incorporate sparsity, low-rank, proximal gradient methods sparsity constraints in addition to the rank. That is, we learn distance metrics B = AAT such that A 2 RN×r for a 1. INTRODUCTION given r N and A is sparse. A sparse A has computa- tional benefits like low storage and computational complex- Learning “good distance” metrics for signals is key in real- ity. Consequently, this work could be useful in sparse low- world applications, such as data classification and retrieval. rank matrix factorization which has numerous applications in For instance, in the k-nearest-neighbor (KNN) classifier, we machine learning including learning [7] and deep neural net- identify the k-nearest labeled images given a test image in the works (deep learning) [8] and autoencoding. This work is also space of visual features. Hence, it is important to learn met- related to optimizing projection matrices introduced in [9]. rics that capture the similarity as well as the dissimilarity of Our approach can also incorporate additional convex con- datasets. Interestingly, several works have shown that prop- straints on A. To illustrate our algorithm, we use a symmet- erly chosen distance metrics can significantly benefit KNN ric and non-smooth version of the MLP (1) in the manner accuracy as compared to the usual Euclidean metric [1–3]. of [4, 5]. We then use the Nesterov smoothing approach to In the standard metricp learning problem (MLP) we learn obtain a smooth cost that has approximation guarantees to the T N a (semi-) norm kxkB = x Bx that respects data x 2 R original problem, followed by Burer-Monteiro splitting [10] dissimilarity constraints on a set D while obtaining the best with quasi-Newton enhancements. Even without the sparsity similarity on a set S: constraints, our algorithmic approach is novel and leads to X 2 improved results over the previous state-of-the-art. min kxi − xjkB B0 (xi;xj )2S The paper is organized as follows. Section 2 sets up the X (1) notation used in the paper and introduces the needed defini- subject to kx − x k2 ≥ 1: i j B tions; while Section 3 describes the problem and its reformu- (xi;xj )2D lation into an appropriate optimization framework. Section This work was supported in part by the European Commission un- 4 states the algorithm and its theoretical background; and its der Grant MIRG-268398, ERC Future Proof, SNF 200021-132548, SNF followed by Section 5 which showcases the experimental re- 200021-146750 and SNF CRSII2-147633. The author names are in alpha- betical order. sults. Section 6 concludes the paper. N×N M 2. PRELIMINARIES Let us define a linear transform A : S+ ! R as T Notation: We denote integer scalars by lowercase letters A (B) := diag V BV , where diag(H) denotes a vector (e.g., i; k; r; p), real scalars by lowercase Greek letters (e.g., of the entries of the principal diagonal of the matrix H. α; δ; λ), sets by uppercase calligraphic letters (e.g., S), vec- Learning the B that minimizes δ for our symmetric MLP tors by lowercase boldface letter (e.g., x) and matrices by (1) therefore becomes the following non-convex problem: N×N uppercase boldface letter (e.g., X). We denote S+ as the min kA (B) − 1M k1 set of positive semidefinite (PSD) matrices. The usual `1 B (6) norm and `0 pseudo-norm (number of non-zero entries) are subject to B 0; rank(B) = r: extended to matrices by reshaping the matrix to a vector. In Section 3, we reformulate (1) into a problem that is Instead of learning B directly, we instead opt to learn tightly connected with learning Johnson-Lindenstrauss (JL) its factors, i.e., B = AAT , which is also known as Burer- embeddings or restricted isometry property (RIP) dimension- Monteiro splitting [10]: Φ 2 r×N p ality reduction. A matrix R is a JL embedding of T p min kA AA − 1M k1 (7) points, X := fxig , if r = O (log p) and there exists a pos- N×r i=1 A2R itive constant δ > 0 such that the following relations holds: The advantages of the non-convex formulation (7) is two fold: 2 2 2 (1−δ)kxi−xjk2 ≤ kΦ(xi−xj)k2 ≤ (1+δ)kxi−xjk2; (2) (i) it reduces storage space since the optimization variable lives in a much lower dimensional space (i.e., N × r N × for every x ; x 2 X , x 6= x [11, 12]. Using the definition i j i j N), and (ii) it enables us to add additional constraints and of the metric in Section 1, we can rewrite (2) as follows: regularizers on the factors A directly. 2 2 2 (1 − δ)kxi − xjk2 ≤ kxi − xjkB ≤ (1 + δ)kxi − xjk2; (3) For instance, while the rank constraints can be achieved by constraining that the dimension of A be N × r, we can where B = ΦT Φ. Without loss of generality, to simplify the also consider adding an ` -norm constraint as well as an ` - algebra, we are going to enforce the similarity or dissimilarity 0 1 regularizer term (as in [15]) to have the following more gen- constraints on normalized differences of data points: eral formulation. Definition 1. Given X ⊂ N we define the set of secants R T min kA AA − 1M k1 + λkAk1 vectors of points xi; xj 2 X with xi 6= xj as: N×r A2R (8) xi − xj subject to: kAk0 ≤ σ: S(X ) := vij = : (4) kxi − xjk2 The `0-norm constraint enables us to specify a priori the spar- sity of the output of our algorithm. It is also possible to add a 3. PROBLEM DESCRIPTION constraint on the Frobenius norm of A directly. In this section, we set up the basic optimization problem that Note that the approach in [4] solves a convex relaxation reveals the computational difficulty of (1). In general, the of (6), where the rank constraint is replaced by a nuclear norm MLP (1) considers relationships between points based on constraint. That solution works in the N × N space and their pairwise distances. Hence, we would require that the requires eigendecompositions. In contrast, we do not do a metric B preserves the pairwise distances of the points in D eigendecomposition in our approach to recover A. Moreover, up to a distortion parameter δ as in (3) to yield a more strin- we can strictly enforce rank constraints while minimizing δ. gent constraint for (1) while ignoring this requirement for Unfortunately, our problem (8) is not smooth and hence points in S. However, we set up a symmetric problem which we only have access to a subgradient of the objective. Instead, then uses RIP in the manner of [4, 5] that can be adjusted we consider the following smoothed version: depending on the individual application. T min f(A AA − 1M ) + λkAk1 N×r In this symmetric formulation, using secant vectors, (3) A2R (9) simplifies to jvT Bv − 1j ≤ δ for x ; x 2 X with x 6= x . ij ij i j i j subject to: kAk0 ≤ σ: p Re-indexing the vij to vl for l = 1;:::;M, where M = 2 , 2 we form the set of M secant vectors S(X ) = fv1;:::; vM g The simplest choice of a smoothing function is f(z) = kzk2 into an N × M matrix V = [v1;:::; vM ]. Then we learn a which can be interpreted as penalizing the average δ for all se- T B that minimizes jvl Bvl − 1j (for a slight abuse of notation cant vectors. In this paper, we focus on the smoothing func- PM zi/µ −zi/µ we will refer to this quantity as δ) over all vl 2 S(X ).
Load more

Recommended publications
  • Anastasios Kyrillidis
    Anastasios Kyrillidis CONTACT 3119 Duncan Hall INFORMATION 6100 Main Street, 77005 Tel: (+1) 713-348-4741 Houston, United States E-mail: [email protected] Website: akyrillidis.github.io RESEARCH Optimization for machine learning, convex and non-convex analysis and optimization, structured low dimensional INTERESTS models, large-scale computing, quantum computing. CADEMIC Rice University, Houston, USAA APPOINTMENTS Noah Harding Assistant Professor at Computer Science Dept. July 2018 - now University of Texas at Austin, Austin, USA Simons Foundation Postdoctoral Researcher November 2014 - August 2017 Member of WNCG PROFESSIONAL IBM T.J. Watson Research Center, New York (USA) APPOINTMENTS Goldstine PostDoctoral Fellow September 2017 - July 2018 EDUCATION Ecole´ Polytechnique F´ed´eralede Lausanne (EPFL), Lausanne, Switzerland Ph.D., School of Computer and Communication Sciences, September 2010 - October 2014. TEACHING AND Instructor SUPERVISING Rice University EXPERIENCE • COMP 414/514 — Optimization: Algorithms, complexity & approximations — Fall ‘19 • Students enrolled: 30 (28 G/2 UG) • Class evaluation — Overall quality: 1.54 (Rice mean: 1.76); Organization: 1.57 (Rice mean: 1.75); Chal- lenge: 1.5 (Rice 1.73) • Instructor evaluation — Effectiveness: 1.43 (Rice mean: 1.67); Presentation: 1.39 (Rice mean: 1.73); Knowledge: 1.29 (Rice mean: 1.56). — Fall ‘20 • Students enrolled: 30 (8 G/22 UG) • Class evaluation — Overall quality: 1.29 (Rice mean: 1.69); Organization: 1.28 (Rice mean: 1.69); Chal- lenge: 1.31 (Rice 1.68) • Instructor evaluation — Effectiveness: 1.21 (Rice mean: 1.58); Presentation: 1.17 (Rice mean: 1.63); Knowledge: 1.14 (Rice mean: 1.49). • COMP 545 — Advanced topics in optimization: From simple to complex ML systems — Spring ‘19 • Students enrolled: 10 • Class evaluation — Overall quality: 1.31 (Rice mean: 1.78); Organization: 1.23 (Rice mean: 1.79); Chal- lenge: 1.46 (Rice mean: 1.75).
    [Show full text]
  • University of California San Diego
    UNIVERSITY OF CALIFORNIA SAN DIEGO Sparse Recovery and Representation Learning A dissertation submitted in partial satisfaction of the requirements for the degree Doctor of Philosophy in Mathematics by Jingwen Liang Committee in charge: Professor Rayan Saab, Chair Professor Jelena Bradic Professor Massimo Franceschetti Professor Philip E. Gill Professor Tara Javidi 2020 Copyright Jingwen Liang, 2020 All rights reserved. The dissertation of Jingwen Liang is approved, and it is ac- ceptable in quality and form for publication on microfilm and electronically: Chair University of California San Diego 2020 iii DEDICATION To my loving family, friends and my advisor. iv TABLE OF CONTENTS Signature Page . iii Dedication . iv Table of Contents . .v List of Figures . vii Acknowledgements . viii Vita .............................................x Abstract of the Dissertation . xi Chapter 1 Introduction and Background . .1 1.1 Compressed Sensing and low-rank matrix recovery with prior infor- mations . .1 1.2 Learning Dictionary with Fast Transforms . .3 1.3 Deep Generative Model Using Representation Learning Techniques5 1.4 Contributions . .6 Chapter 2 Signal Recovery with Prior Information . .8 2.1 Introduction . .8 2.1.1 Compressive Sensing . .9 2.1.2 Low-rank matrix recovery . 10 2.1.3 Prior Information for Compressive Sensing and Low-rank matrix recovery . 12 2.1.4 Related Work . 13 2.1.5 Contributions . 21 2.1.6 Overview . 22 2.2 Low-rank Matrices Recovery . 22 2.2.1 Problem Setting and Notation . 22 2.2.2 Null Space Property of Low-rank Matrix Recovery . 23 2.3 Low-rank Matrix Recovery with Prior Information . 31 2.3.1 Support of low rank matrices .
    [Show full text]
  • This Booklet
    Applied Mathematics Department of Mathematical Sciences Research Projects 2018-2019 2 Forecasting solar and wind power outputs using deep learning approaches Research Team: Dr Bubacarr Bah In collaboration with University of Pretoria Highlights Identification of suitable locations of wind and solar farms in South Africa. Prediction of wind (solar) power from historical wind (solar) data, and other environmental factors, of South Africa using recurrent neural networks. Kalle Pihlajasaari / Wikimedia Commons / CC-BY-SA-3.0 Figure. Wind turbines at Darling, Western Cape. Applications Informed decision making by power producer in terms of integra- tion of renewable energies into existing electricity grids. Forecasting of energy prices. 3 Machine learning outcome prediction for coma patients Research Team: Dr Bubacarr Bah In collaboration with University of Cape Town Highlights Outcome prediction with Serial Neuron-Specific Enolase (SNSE) measurements from coma patients. The use of k-nearest neighbors (k-NN) for imputation of missing data shows promising results. Outcome prediction with EEG signals from coma patients. Using machine learning to determine the prognostic power of SNSE and EEG Figure. EEG and the determination of level of consciousness in coma patients. Applications Potential application in medical and health systems to improve diag- nosis (and treatment) of coma. 4 Data-driven river flow routing using deep learning Research Team: Dr Willie Brink and Prof Francois Smit MSc Student: Jaco Briers Highlights Predicting flow along the lower Orange River in South Africa, for improved release scheduling at the Vanderkloof Dam, using recur- rent neural networks as well as feedforward convolutional neural networks trained on historical time series records.
    [Show full text]
  • Tuesday July 9, 1.45-8.00 Pm
    Tuesday July 9, 1.45-8.00 pm 1.45-2.45 Combinatorial compressed sensing with expanders Bubacarr Bah Wegener Chair: Ana Gilbert Deep learning (invited session) Chair: Misha Belkin & Mahdi Soltanolkotabi 2:55-3:20 Reconciling modern machine learning practice and the classical bias-variance trade-off Mikhail Belkin, Daniel Hsu, Siyuan Ma & Soumik Mandal 3.20-3.45 Overparameterized Nonlinear Optimization with Applications to Neural Nets Samet Oymak 3.45-4.10 General Bounds for 1-Layer ReLU approximation Bolton R. Bailey & Matus Telgarsky 4.10-4.20 Short Break A9 Amphi 1 4.20-4.45 Generalization in deep nets: an empirical perspective Tom Goldstein 4.45-5.10 Neuron birth-death dynamics accelerates gradient descent and converges asymptotically Joan Bruna 5.45-8.00 Poster simposio Domaine du Haut-Carr´e Tuesday July 9, 1.45-8.00 pm 1.45-2.45 Combinatorial compressed sensing with expanders Bubacarr Bah Wegener Chair: Anna Gilbert Frame Theory Chair: Ole Christensen 2.55-3.20 Banach frames and atomic decompositions in the space of bounded operators on Hilbert spaces Peter Balazs 3.20-3.45 Frames by Iterations in Shift-invariant Spaces Alejandra Aguilera, Carlos Cabrelli, Diana Carbajal & Victoria Paternostro 3.45-4.10 Frame representations via suborbits of bounded operators Ole Christensen & Marzieh Hasannasabjaldehbakhani 4.10-4.20 Short Break 4.20-4.45 Sum-of-Squares Optimization and the Sparsity Structure A29 Amphi 2 of Equiangular Tight Frames Dmitriy Kunisky & Afonso Bandeira 4.45-5.10 Frame Potentials and Orthogonal Vectors Josiah Park 5.10-5.35
    [Show full text]
  • DIFFUSION MAPS 43 5.1 Clustering
    Di®usion Maps: Analysis and Applications Bubacarr Bah Wolfson College University of Oxford A dissertation submitted for the degree of MSc in Mathematical Modelling and Scienti¯c Computing September 2008 This thesis is dedicated to my family, my friends and my country for the unflinching moral support and encouragement. Acknowledgements I wish to express my deepest gratitude to my supervisor Dr Radek Erban for his constant support and valuable supervision. I consider myself very lucky to be supervised by a person of such a wonderful personality and enthusiasm. Special thanks to Prof I. Kevrekidis for showing interest in my work and for motivating me to do Section 4.3 and also for sending me some material on PCA. I am grateful to the Commonwealth Scholarship Council for funding this MSc and the Scholarship Advisory Board (Gambia) for nominating me for the Commonwealth Scholarship award. Special thanks to the President Alh. Yahya A.J.J. Jammeh, the SOS and the Permanent Secretary of the DOSPSE for being very instrumental in my nomination for this award. My gratitude also goes to my employer and former university, University of The Gambia, for giving me study leave. I appreciate the understanding and support given to me by my wife during these trying days of my studies and research. Contents 1 INTRODUCTION 2 1.1 The dimensionality reduction problem . 2 1.1.1 Algorithm . 4 1.2 Illustrative Examples . 5 1.2.1 A linear example . 5 1.2.2 A nonlinear example . 8 1.3 Discussion . 9 2 THE CHOICE OF WEIGHTS 13 2.1 Optimal Embedding .
    [Show full text]
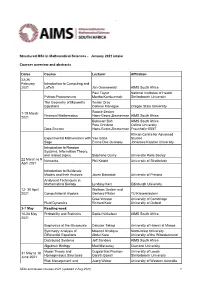
  • Structured Msc in Mathematical Sciences - January 2021 Intake
    ` Structured MSc in Mathematical Sciences - January 2021 intake Courses overview and abstracts Dates Course Lecturer Affiliation 22-26 February Introduction to Computing and 2021 LaTeX Jan Groenewald AIMS South Africa Paul Taylor National Institutes of Health Python Programming Martha Kamkuemah Stellenbosch University The Geometry of Maxwell’s Tevian Dray Equations Corinne Manogue Oregon State University 1-19 March Ronnie Becker Financial Mathematics Hans-Georg Zimmerman AIMS South Africa 2021 Bubacarr Bah AIMS South Africa Pete Grindrod Oxford University Data Science Hans-Georg Zimmerman Fraunhofer IBMT African Centre for Advanced Experimental Mathematics with Yae Gaba Studies Sage Evans Doe Ocansey Johannes Keppler University Introduction to Random Systems, Information Theory, and related topics Stéphane Ouvry Université Paris Saclay 22 March to 9 Networks Phil Knight University of Strathclyde April 2021 Introduction to Multiscale Models and their Analysis Jacek Banasiak University of Pretoria Analytical Techniques in Mathematical Biology Lyndsay Kerr Edinburgh University 12- 30 April Wolfram Decker and 2021 Computational Algebra Gerhard Pfister TU Kaiserslautern Grae Worster University of Cambridge Fluid Dynamics Richard Katz University of Oxford 3-7 May Reading week 10-28 May Probability and Statistics Daniel Nickelsen AIMS South Africa 2021 Biophysics at the Microscale Daisuke Takagi University of Hawaii at Manoa Symmetry Analysis of Masood Khalique North-West University Differential Equations Abdul Kara University of the Witwatersrand
    [Show full text]
  • Bubacarr Bah CV
    Curriculum Vitae of Bubacarr Bah Address African Institute for Mathematical Sciences (AIMS) South Africa 6 Melrose Road Muizenberg 7945 South Africa Recent Employment History Oct 2016 { present German Research Chair (Senior Researcher) in Mathematics of Data Science, AIMS South Africa, & Senior Lecturer (Asst. Prof.), Stellenbosch University Sep 2014 { Sep 2016 Postdoctoral Fellow, Mathematics Department, & Institute for Computational Engineering & Sciences, University of Texas in Austin Sep 2012 { Aug 2014 Research Scientist (postdoc), Laboratory for Information and Inference Systems, Ecole Polytechnique Federale de Lausanne (EPFL) Education Sep 2008 { Aug 2012 PhD in Applied and Computational Mathematics, University of Edinburgh, UK Sep 2007 { Sep 2008 MSc in Mathematical Modelling & Scientific Computing, University of Oxford, UK Jan 2000 { Aug 2004 BSc in Mathematics and Physics, (summa cum laude), University of The Gambia Honours 2020 Alexander von Humboldt Award of German Research Chair Mathematics at AIMS South Africa 2016 Alexander von Humboldt Award of German Research Chair Mathematics at AIMS South Africa 2015 NSF-funded SIAM ICIAM15 Travel Award 2013 Travel Grant for Matheon Workshop 2013 on Compressed Sensing & its Applications 2011 SIAM Certificate of Recognition 2010 SIAM Best Student Paper Prize 2008 Edinburgh University Principal's Scholarship for PhD studies 2007 Commonwealth Scholarship for MSc studies 2005 Overall Best Student (valedictorian) Award 2005 Best Student of the Faculty of Science & Agriculture Award 2005 Vice Chancellor's Award Journal Publications 1. Improved restricted isometry constant bounds for Gaussian matrices; SIAM Journal on Matrix Analysis, Vol. 31(5) (2010) 2882{2898 (with J. Tanner). 2. Bounds of restricted isometry constants in extreme asymptotics: formulae for Gaussian matrices; Linear Algebra and its Applications, Vol.
    [Show full text]
  • Full Report (Pdf)
    Recognising African Excellence in Machine Learning The Inaugural Kambule and Maathai Awards August 2018 The Deep Learning Indaba 7/31/2018 Awards-Report-2018-markup - Google Docs Recognising African Excellence in Machine Learning: The Inaugural Kambule and Maathai Awards 2018 Issued August 2018. 2018. The Deep Learning Indaba. Typeset in Maven Pro. Corresponding Authors: Daniela Massiceti and Shakir Mohamed Contact: [email protected] This report can be viewed online at deeplearningindaba.com/reports Indaba Abantu Shakir Mohamed, DeepMind Ulrich Paquet, DeepMind Vukosi Marivate, University of Pretoria Willie Brink, Stellenbosch University Nyalleng Moorosi, Google AI Ghana Stephan Gouws, DeepMind Benjamin Rosman, Council for Scientific and Industrial research (CSIR), and University of the Witwatersrand Richard Klein, University of the Witwatersrand Avishkar Bhoopchand, DeepMind Kathleen Siminyu, Africa’s Talking Muthoni Wanyoike, InstaDeep, Kenya. Daniela Massiceti, University of Oxford Herman Kamper, Stellenbosch University 1 https://docs.google.com/document/d/1cD_XexDztnNAAKBa91d5l1CT16NGF5BUynL98RoaUMM/edit#heading=h.j5ghgepwl09f 2/17 7/31/2018 Awards-Report-2018-markup - Google Docs A Personal Message Reflecting on the outcomes of each of our programmes gives us the welcome and needed opportunity to examine our work with fresh eyes, to review how our programmes work together, and to think about what our programmes mean to us personally. For us, the creation of the Kambule and Maathai awards have been an instrument with which
    [Show full text]
  • AIMS Annual Report TEXT.Indd
    ANNUAL REPORT 2019 ABOUT US The African Institute for Mathematical Sciences (AIMS) is a pan-African network of centres of excellence for postgraduate education, research and public engagement in mathematical sciences. Its mission is to enable Africa’s brightest students to flourish as independent thinkers, problem solvers and innovators capable of driving Africa’s future scientific, educational and economic self-sufficiency. AIMS was founded in Cape Town, South Africa, in 2003. Since then AIMS centres have opened in Senegal (2011), Ghana (2012), Cameroon (2013) and Rwanda (2016). The pan-African network of AIMS centres is coordinated by the AIMS Next Einstein Initiative (AIMS-NEI).* This is the annual report of AIMS South Africa for the period 1 August 2018 to 31 July 2019. It includes an overview of all activities of AIMS South Africa and its associated projects, as well as the financial statements for the 2018 calendar year. Since AIMS South Africa opened in 2003, 812 students, of which 34% are women, from 38 different African countries have graduated from its core academic programme. AIMS South Africa has local association with the Universities of Cape Town (UCT), Stellenbosch (SU) and the Western Cape (UWC) and international association with the Universities of Cambridge, Oxford and Paris-Sud. AIMS South Africa offers: • An intensive one-year structured Master’s in Mathematical Sciences with intakes in August and January. • Specialised courses as part of regular postgraduate programmes at South African universities. • A well-established research centre which hosts regular workshops and conferences. • Professional development programmes for teachers. • Public engagement activities. * AIMS Next Einstein Initiative, Kigali, Rwanda, Email: [email protected].
    [Show full text]
  • Restricted Isometry Constants in Compressed Sensing
    Restricted Isometry Constants in Compressed Sensing Bubacarr Bah Doctor of Philosophy University of Edinburgh 2012 Declaration I declare that this thesis was composed by myself and that the work contained therein is my own, except where explicitly stated otherwise in the text. (Bubacarr Bah) 3 To my grandmother, Mama Juma Sowe. 4 Acknowledgement I wish to express my deepest gratitude to my supervisor, Professor Jared Tanner, for his guid- ance and support during the course of my PhD. I would follow this with special thanks to my second supervisor, Dr. Coralia Cartis, for her regular monitoring of my progress and her encouragement. Further special thanks to my sponsor the University of Edinburgh through the MTEM Scholarships created in 2007 by the Principal, Professor Sir Timothy O’Shea. My sincere gratitude goes to Professor Endre Suli of Oxford University who informed me of, and recommended me for, this PhD opening with Professor Jared Tanner and also to my MSc dissertation supervisor, Dr. Radek Erban of Oxford University, for recommending me for this PhD programme. Many thanks to both the admin and support staff of the School of Mathematics, University of Edinburgh, that contributed to making my PhD programme proceed smoothly. Similar thanks go to members of the Mathematics Teaching Organisation of the school. I would like to thank the following people for contributing to my research either by responding to a question I posed, discussing an issue pertaining to my research or giving me feedback on my research: Dennis Amelunxen, Jeff Blanchard, Burak Burke, Prof. David Donoho, Martin Lotz, Andrew Thompson, Ke Wei, Pavel Zhlobich.
    [Show full text]
  • Artificial Intelligence and Data Science for Society Special Track
    Artificial Intelligence and Data Science for Society Special Track International Conference on Intelligent Systems Design and Applications (ISDA 2019), Dec 2019 Session Information The use of Artificial Intelligence (AI) and Data Science (DS) approaches to tackle social challenges has been receiving attention over the last few years. This entails using Machine Learning, Statistics, Mathematics, and other related tools to tackle challenges that lead to Social Impact. This is exemplified by organisations that work with government, NGOs, private entities with the sole purpose of affecting some process that is a public good or at least has externalities that are public good. Overall this encompasses more than just using Data Science in social good settings; it involves understanding society, factors that contribute to or impede progress, building skill for public servants, creating receptive environments, sharing experiences within the sector with other and more. Covering all these factors is in the pursuit of having lasting impact. There are different paradigms being used to tackle problems in different areas and there is value in learning the insights gained in all these areas. We aim to provide a session where practitioners, industrial representatives and researchers in this field can share their experiences, present current research results and discuss the modelling or analysis in various problem areas. Goal 1: Research papers This session invites full research papers covering AI/DS Research, Practice & Capacity building in: ● Food, water, and utilities ● Public safety and disaster relief ● Inclusiveness ● Ethical issues, fairness in Machine Learning or Artificial Intelligence ● Efficiency and sustainability ● Government transparency ● Economic, social, and personal development ● Transportation ● Energy ● Smart cities ● Education ● Social services, unemployment and homelessness ● Healthcare ● Policymaking ● Environment ● And more….
    [Show full text]
  • Sparse Matrices for Weighted Sparse Recovery
    Sparse matrices for weighted sparse recovery Bubacarr Bah ∗ August 13, 2018 Abstract We derived the first sparse recovery guarantees for weighted ℓ1 minimization with sparse random matrices and the class of weighted sparse signals, using a weighted versions of the null space property to derive these guarantees. These sparse matrices from expender graphs can be applied very fast and have other better computational complexities than their dense counterparts. In addition we show that, using such sparse matrices, weighted sparse recovery with weighted ℓ1 minimization leads to sample complexities that are linear in the weighted sparsity of the signal and these sampling rates can be smaller than those of standard sparse recovery. Moreover, these results reduce to known results in standard sparse recovery and sparse recovery with prior information and the results are supported by numerical experiments. Keywords: Compressed sensing, sparse recovery, weighted ℓ1-minimization, weighted sparsity, sparse matrix, expander graph, sample complexity, nullspace property 1 Introduction Weighted sparse recovery was introduced by [26] for application to function interpolation but there has been a steady growth in interest in the area, [1, 2, 5, 7, 15, 25], since then. In particular [5] showed its equivalence to standard sparse recovery using weighted ℓ1 minimization. The setting considered here is as follows: for a signal of interest x RN ∈ which is k-sparse and a given measurement matrix A Rn×N , we perform measurements arXiv:1604.01067v2 [math.NA] 9 May 2016 ∈ y = Ax + e for a noise vector e with e η (this being the main difference with the k k1 ≤ previously mentioned works).
    [Show full text]