University of California San Diego
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

IAMG Newsletter IAMG Newsletter
No. 101 December 2020 IAMGIAMG NewsletterNewsletter Official Newsletter of the International Association for Mathematical Geosciences Contents ow, what a strange year! WYet with international Submit nominationS for 2021 GeorGeS matheron Lectur- travel stopped, conferences er and 2022 iamG diStinGuiShed Lecturer ................. 1 postponed, and campuses diStinGuiShed Lecturer updateS ....................................... 1 closed we’ve adapted. As can preSident’S forum .............................................................. 3 be expected, we’re a little light on news. Hopefully 2021 is a much better year worldwide! In member newS ...................................................................... 4 the meantime, hopefully you enjoy the cartoons below. paSt preSident prof Jenny mcKinLey eLection to the iuGS I’d like to welcome Peter Dowd and our new IAMG council and executive counciL ......................................................... 4 thank Jenny McKinley and a our outgoing council for all their SprinGer encycLopedia of mathematicaL GeoScienceS .. 4 hard work over the last four years. prince SuLtan bin abduLaziz internationaL Katie Silversides water prize .................................................................... 4 <> ieee GeoScience and remote SenSinG Society (GrSS) diS- tinGuiShed Lecturer (dL) ............................................. 4 diverSity and incLuSion in GeoScience ............................. 4 Student newS ...................................................................... 5 nancy Student -

Anastasios Kyrillidis
Anastasios Kyrillidis CONTACT 3119 Duncan Hall INFORMATION 6100 Main Street, 77005 Tel: (+1) 713-348-4741 Houston, United States E-mail: [email protected] Website: akyrillidis.github.io RESEARCH Optimization for machine learning, convex and non-convex analysis and optimization, structured low dimensional INTERESTS models, large-scale computing, quantum computing. CADEMIC Rice University, Houston, USAA APPOINTMENTS Noah Harding Assistant Professor at Computer Science Dept. July 2018 - now University of Texas at Austin, Austin, USA Simons Foundation Postdoctoral Researcher November 2014 - August 2017 Member of WNCG PROFESSIONAL IBM T.J. Watson Research Center, New York (USA) APPOINTMENTS Goldstine PostDoctoral Fellow September 2017 - July 2018 EDUCATION Ecole´ Polytechnique F´ed´eralede Lausanne (EPFL), Lausanne, Switzerland Ph.D., School of Computer and Communication Sciences, September 2010 - October 2014. TEACHING AND Instructor SUPERVISING Rice University EXPERIENCE • COMP 414/514 — Optimization: Algorithms, complexity & approximations — Fall ‘19 • Students enrolled: 30 (28 G/2 UG) • Class evaluation — Overall quality: 1.54 (Rice mean: 1.76); Organization: 1.57 (Rice mean: 1.75); Chal- lenge: 1.5 (Rice 1.73) • Instructor evaluation — Effectiveness: 1.43 (Rice mean: 1.67); Presentation: 1.39 (Rice mean: 1.73); Knowledge: 1.29 (Rice mean: 1.56). — Fall ‘20 • Students enrolled: 30 (8 G/22 UG) • Class evaluation — Overall quality: 1.29 (Rice mean: 1.69); Organization: 1.28 (Rice mean: 1.69); Chal- lenge: 1.31 (Rice 1.68) • Instructor evaluation — Effectiveness: 1.21 (Rice mean: 1.58); Presentation: 1.17 (Rice mean: 1.63); Knowledge: 1.14 (Rice mean: 1.49). • COMP 545 — Advanced topics in optimization: From simple to complex ML systems — Spring ‘19 • Students enrolled: 10 • Class evaluation — Overall quality: 1.31 (Rice mean: 1.78); Organization: 1.23 (Rice mean: 1.79); Chal- lenge: 1.46 (Rice mean: 1.75). -

25Th International Joint Conference on Artif Icial Intelligence New York
25th International Joint Conference on Artificial Intelligence New York City, July 9–15, 2016 www.ijcai-16.org Organizing Institutions IJCAI AAAI The International Joint Conferences on Artificial Intelligence The Association for the Advancement of Artificial Intelligence IJCAI-16 Welcome to IJCAI 2016 Welcome to the Twenty-fifth International The conference includes workshops, tuto- Joint Conference on Artificial Intelligence! rials, exhibitions, demonstrations, invited talks, and paper/poster presentations. On We are delighted to welcome you to New Friday there will be an Industry Day, with York, one of the most exciting cities of presentations from the top AI companies; the world, to take part in IJCAI, the leading and there will be an AI Festival, open to conference on the thrilling field of Artificial the public, consisting of the IJCAI award Intelligence. AI today has a tremendous winner’s talks. You will not want to miss out impact. It is in all the media and makes a on this highlight, so plan to stay at IJCAI-16 real difference. At IJCAI-16, you will have the until the very end. opportunity to meet some of the world’s leading AI researchers, to learn first-hand The conference (including workshops about their newest research results and and tutorials) takes place at the Hilton in developments, and to catch up with current midtown Manhattan. The Hilton is just a AI trends in science and industry. And, of ten-minute walk from Central Park, where course, IJCAI-16 will be the perfect forum the conference banquet will be held, for presenting your own achievements, and half a block from the world-famous both to specialists in your field, and to the Museum of Modern Art, where we will have AI world in general. -

Vanderbiltuniversitymedicalcenter
VanderbiltUniversityMedicalCenter Medical Center Medical Center School of Medicine Hospital and Clinic Vanderbilt University 2008/2009 Containing general information and courses of study for the 2008/2009 session corrected to 30 June 2008 Nashville The university reserves the right, through its established procedures, to modify the require- ments for admission and graduation and to change other rules, regulations, and provisions, including those stated in this bulletin and other publications, and to refuse admission to any student, or to require the withdrawal of a student if it is determined to be in the interest of the student or the university. All students, full- or part-time, who are enrolled in Vanderbilt courses are subject to the same policies. Policies concerning noncurricular matters and concerning withdrawal for medical or emo- tional reasons can be found in the Student Handbook, which is on the Vanderbilt Web site at www.vanderbilt.edu/student_handbook. NONDISCRIMINATION STATEMENT In compliance with federal law, including the provisions of Title IX of the Education Amend- ments of 1972, Title VI of the Civil Rights Act of 1964, Sections 503 and 504 of the Reha- bilitation Act of 1973, and the Americans with Disabilities Act of 1990, Vanderbilt University does not discriminate on the basis of race, sex, religion, color, national or ethnic origin, age, disability, or military service in its administration of educational policies, programs, or activ- ities; its admissions policies; scholarship and loan programs; athletic or other university- administered programs; or employment. In addition, the university does not discriminate on the basis of sexual orientation consistent with university non-discrimination policy. -

2017 Medford/Somerville Massachusetts
161ST Commencement Tufts University Sunday, May 21, 2017 Medford/Somerville Massachusetts Commencement 2017 Commencement 2017 School of Arts and Sciences School of Engineering School of Medicine and Sackler School of Graduate Biomedical Sciences School of Dental Medicine The Fletcher School of Law and Diplomacy Cummings School of Veterinary Medicine The Gerald J. and Dorothy R. Friedman School of Nutrition Science and Policy Jonathan M. Tisch College of Civic Life #Tufts2017 commencement.tufts.edu Produced by Tufts Communications and Marketing 17-653. Printed on recycled paper. Table of Contents Welcome from the President 5 Overview of the Day 7 Graduation Ceremony Times and Locations 8 University Commencement 11 Dear Alma Mater 14 Tuftonia’s Day Academic Mace Academic Regalia Recipients of Honorary Degrees 15 School of Arts and Sciences 21 Graduate School of Arts and Sciences School of Engineering School of Medicine and Sackler School 65 of Graduate Biomedical Sciences Public Health and Professional 78 Degree Programs School of Dental Medicine 89 The Fletcher School of Law 101 and Diplomacy Cummings School of Veterinary Medicine 115 The Gerald J. and Dorothy R. Friedman 123 School of Nutrition Science and Policy COMMENCEMENT 2017 3 Welcome from the President This year marks the 161st Commencement exercises held at Tufts University. This is always the high point of the academic year, and we welcome all of you from around the world to campus for this joyous occasion—the culmination of our students’ intellectual and personal journeys. Today’s more than 2,500 graduates arrived at Tufts with diverse backgrounds and perspectives. They have followed rigorous courses of study on our four Massachusetts campuses while enriching the life of our academic community. -

This Booklet
Applied Mathematics Department of Mathematical Sciences Research Projects 2018-2019 2 Forecasting solar and wind power outputs using deep learning approaches Research Team: Dr Bubacarr Bah In collaboration with University of Pretoria Highlights Identification of suitable locations of wind and solar farms in South Africa. Prediction of wind (solar) power from historical wind (solar) data, and other environmental factors, of South Africa using recurrent neural networks. Kalle Pihlajasaari / Wikimedia Commons / CC-BY-SA-3.0 Figure. Wind turbines at Darling, Western Cape. Applications Informed decision making by power producer in terms of integra- tion of renewable energies into existing electricity grids. Forecasting of energy prices. 3 Machine learning outcome prediction for coma patients Research Team: Dr Bubacarr Bah In collaboration with University of Cape Town Highlights Outcome prediction with Serial Neuron-Specific Enolase (SNSE) measurements from coma patients. The use of k-nearest neighbors (k-NN) for imputation of missing data shows promising results. Outcome prediction with EEG signals from coma patients. Using machine learning to determine the prognostic power of SNSE and EEG Figure. EEG and the determination of level of consciousness in coma patients. Applications Potential application in medical and health systems to improve diag- nosis (and treatment) of coma. 4 Data-driven river flow routing using deep learning Research Team: Dr Willie Brink and Prof Francois Smit MSc Student: Jaco Briers Highlights Predicting flow along the lower Orange River in South Africa, for improved release scheduling at the Vanderkloof Dam, using recur- rent neural networks as well as feedforward convolutional neural networks trained on historical time series records. -

Tuesday July 9, 1.45-8.00 Pm
Tuesday July 9, 1.45-8.00 pm 1.45-2.45 Combinatorial compressed sensing with expanders Bubacarr Bah Wegener Chair: Ana Gilbert Deep learning (invited session) Chair: Misha Belkin & Mahdi Soltanolkotabi 2:55-3:20 Reconciling modern machine learning practice and the classical bias-variance trade-off Mikhail Belkin, Daniel Hsu, Siyuan Ma & Soumik Mandal 3.20-3.45 Overparameterized Nonlinear Optimization with Applications to Neural Nets Samet Oymak 3.45-4.10 General Bounds for 1-Layer ReLU approximation Bolton R. Bailey & Matus Telgarsky 4.10-4.20 Short Break A9 Amphi 1 4.20-4.45 Generalization in deep nets: an empirical perspective Tom Goldstein 4.45-5.10 Neuron birth-death dynamics accelerates gradient descent and converges asymptotically Joan Bruna 5.45-8.00 Poster simposio Domaine du Haut-Carr´e Tuesday July 9, 1.45-8.00 pm 1.45-2.45 Combinatorial compressed sensing with expanders Bubacarr Bah Wegener Chair: Anna Gilbert Frame Theory Chair: Ole Christensen 2.55-3.20 Banach frames and atomic decompositions in the space of bounded operators on Hilbert spaces Peter Balazs 3.20-3.45 Frames by Iterations in Shift-invariant Spaces Alejandra Aguilera, Carlos Cabrelli, Diana Carbajal & Victoria Paternostro 3.45-4.10 Frame representations via suborbits of bounded operators Ole Christensen & Marzieh Hasannasabjaldehbakhani 4.10-4.20 Short Break 4.20-4.45 Sum-of-Squares Optimization and the Sparsity Structure A29 Amphi 2 of Equiangular Tight Frames Dmitriy Kunisky & Afonso Bandeira 4.45-5.10 Frame Potentials and Orthogonal Vectors Josiah Park 5.10-5.35 -

DIFFUSION MAPS 43 5.1 Clustering
Di®usion Maps: Analysis and Applications Bubacarr Bah Wolfson College University of Oxford A dissertation submitted for the degree of MSc in Mathematical Modelling and Scienti¯c Computing September 2008 This thesis is dedicated to my family, my friends and my country for the unflinching moral support and encouragement. Acknowledgements I wish to express my deepest gratitude to my supervisor Dr Radek Erban for his constant support and valuable supervision. I consider myself very lucky to be supervised by a person of such a wonderful personality and enthusiasm. Special thanks to Prof I. Kevrekidis for showing interest in my work and for motivating me to do Section 4.3 and also for sending me some material on PCA. I am grateful to the Commonwealth Scholarship Council for funding this MSc and the Scholarship Advisory Board (Gambia) for nominating me for the Commonwealth Scholarship award. Special thanks to the President Alh. Yahya A.J.J. Jammeh, the SOS and the Permanent Secretary of the DOSPSE for being very instrumental in my nomination for this award. My gratitude also goes to my employer and former university, University of The Gambia, for giving me study leave. I appreciate the understanding and support given to me by my wife during these trying days of my studies and research. Contents 1 INTRODUCTION 2 1.1 The dimensionality reduction problem . 2 1.1.1 Algorithm . 4 1.2 Illustrative Examples . 5 1.2.1 A linear example . 5 1.2.2 A nonlinear example . 8 1.3 Discussion . 9 2 THE CHOICE OF WEIGHTS 13 2.1 Optimal Embedding . -
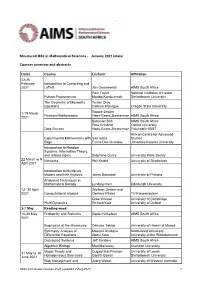
Structured Msc in Mathematical Sciences - January 2021 Intake
` Structured MSc in Mathematical Sciences - January 2021 intake Courses overview and abstracts Dates Course Lecturer Affiliation 22-26 February Introduction to Computing and 2021 LaTeX Jan Groenewald AIMS South Africa Paul Taylor National Institutes of Health Python Programming Martha Kamkuemah Stellenbosch University The Geometry of Maxwell’s Tevian Dray Equations Corinne Manogue Oregon State University 1-19 March Ronnie Becker Financial Mathematics Hans-Georg Zimmerman AIMS South Africa 2021 Bubacarr Bah AIMS South Africa Pete Grindrod Oxford University Data Science Hans-Georg Zimmerman Fraunhofer IBMT African Centre for Advanced Experimental Mathematics with Yae Gaba Studies Sage Evans Doe Ocansey Johannes Keppler University Introduction to Random Systems, Information Theory, and related topics Stéphane Ouvry Université Paris Saclay 22 March to 9 Networks Phil Knight University of Strathclyde April 2021 Introduction to Multiscale Models and their Analysis Jacek Banasiak University of Pretoria Analytical Techniques in Mathematical Biology Lyndsay Kerr Edinburgh University 12- 30 April Wolfram Decker and 2021 Computational Algebra Gerhard Pfister TU Kaiserslautern Grae Worster University of Cambridge Fluid Dynamics Richard Katz University of Oxford 3-7 May Reading week 10-28 May Probability and Statistics Daniel Nickelsen AIMS South Africa 2021 Biophysics at the Microscale Daisuke Takagi University of Hawaii at Manoa Symmetry Analysis of Masood Khalique North-West University Differential Equations Abdul Kara University of the Witwatersrand -

2019 International Joint Conference on Neural Networks (IJCNN 2019)
2019 International Joint Conference on Neural Networks (IJCNN 2019) Budapest, Hungary 14-19 July 2019 Pages 1-774 IEEE Catalog Number: CFP19IJS-POD ISBN: 978-1-7281-1986-1 1/8 Copyright © 2019 by the Institute of Electrical and Electronics Engineers, Inc. All Rights Reserved Copyright and Reprint Permissions: Abstracting is permitted with credit to the source. Libraries are permitted to photocopy beyond the limit of U.S. copyright law for private use of patrons those articles in this volume that carry a code at the bottom of the first page, provided the per-copy fee indicated in the code is paid through Copyright Clearance Center, 222 Rosewood Drive, Danvers, MA 01923. For other copying, reprint or republication permission, write to IEEE Copyrights Manager, IEEE Service Center, 445 Hoes Lane, Piscataway, NJ 08854. All rights reserved. *** This is a print representation of what appears in the IEEE Digital Library. Some format issues inherent in the e-media version may also appear in this print version. IEEE Catalog Number: CFP19IJS-POD ISBN (Print-On-Demand): 978-1-7281-1986-1 ISBN (Online): 978-1-7281-1985-4 ISSN: 2161-4393 Additional Copies of This Publication Are Available From: Curran Associates, Inc 57 Morehouse Lane Red Hook, NY 12571 USA Phone: (845) 758-0400 Fax: (845) 758-2633 E-mail: [email protected] Web: www.proceedings.com TABLE OF CONTENTS COMPARISON OF PROBABILISTIC MODELS AND NEURAL NETWORKS ON PREDICTION OF HOME SENSOR EVENTS ............................................................................................................................................1 Flávia Dias Casagrande ; Jim Tørresen ; Evi Zouganeli CYSTOID FLUID COLOR MAP GENERATION IN OPTICAL COHERENCE TOMOGRAPHY IMAGES USING A DENSELY CONNECTED CONVOLUTIONAL NEURAL NETWORK .....................................9 Plácido L. -

Multi-Instance Pose Networks: Rethinking Top-Down Pose Estimation
Multi-Instance Pose Networks: Rethinking Top-Down Pose Estimation Rawal Khirodkar1∗ Visesh Chari2 Amit Agrawal2 Ambrish Tyagi2 1Carnegie Mellon University 2Amazon Lab 126 [email protected] fviseshc, aaagrawa, [email protected] Abstract A key assumption of top-down human pose estimation approaches is their expectation of having a single per- son/instance present in the input bounding box. This often leads to failures in crowded scenes with occlusions. We propose a novel solution to overcome the limitations of this fundamental assumption. Our Multi-Instance Pose Network (MIPNet) allows for predicting multiple 2D pose instances within a given bounding box. We introduce a Multi-Instance Modulation Block (MIMB) that can adaptively modulate channel-wise feature responses for each instance and is parameter efficient. We demonstrate the efficacy of our ap- proach by evaluating on COCO, CrowdPose, and OCHuman datasets. Specifically, we achieve 70:0 AP on CrowdPose and 42:5 AP on OCHuman test sets, a significant improve- ment of 2:4 AP and 6:5 AP over the prior art, respectively. When using ground truth bounding boxes for inference, MIP- Net achieves an improvement of 0:7 AP on COCO, 0:9 AP on CrowdPose, and 9:1 AP on OCHuman validation sets com- Figure 1: 2D pose estimation networks often fail in presence of pared to HRNet. Interestingly, when fewer, high confidence heavy occlusion. (Left) Bounding boxes corresponding to two per- bounding boxes are used, HRNet’s performance degrades sons. (Middle) For both bounding boxes, HRNet predicts the pose (by 5 AP) on OCHuman, whereas MIPNet maintains a rela- for the front person and misses the occluded person. -

Embodied Question Answering
2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR 2018) Salt Lake City, Utah, USA 18-22 June 2018 Pages 1-731 IEEE Catalog Number: CFP18003-POD ISBN: 978-1-5386-6421-6 1/13 Copyright © 2018 by the Institute of Electrical and Electronics Engineers, Inc. All Rights Reserved Copyright and Reprint Permissions: Abstracting is permitted with credit to the source. Libraries are permitted to photocopy beyond the limit of U.S. copyright law for private use of patrons those articles in this volume that carry a code at the bottom of the first page, provided the per-copy fee indicated in the code is paid through Copyright Clearance Center, 222 Rosewood Drive, Danvers, MA 01923. For other copying, reprint or republication permission, write to IEEE Copyrights Manager, IEEE Service Center, 445 Hoes Lane, Piscataway, NJ 08854. All rights reserved. *** This is a print representation of what appears in the IEEE Digital Library. Some format issues inherent in the e-media version may also appear in this print version. IEEE Catalog Number: CFP18003-POD ISBN (Print-On-Demand): 978-1-5386-6421-6 ISBN (Online): 978-1-5386-6420-9 ISSN: 1063-6919 Additional Copies of This Publication Are Available From: Curran Associates, Inc 57 Morehouse Lane Red Hook, NY 12571 USA Phone: (845) 758-0400 Fax: (845) 758-2633 E-mail: [email protected] Web: www.proceedings.com 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition CVPR 2018 Table of Contents Message from the General and Program Chairs cxviii Organizing Committee and Area