CS 352 Compilers: Principles and Practice
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

SJC – Small Java Compiler
SJC – Small Java Compiler User Manual Stefan Frenz Translation: Jonathan Brase original version: 2011/06/08 latest document update: 2011/08/24 Compiler Version: 182 Java is a registered trademark of Oracle/Sun Table of Contents 1 Quick introduction.............................................................................................................................4 1.1 Windows...........................................................................................................................................4 1.2 Linux.................................................................................................................................................5 1.3 JVM Environment.............................................................................................................................5 1.4 QEmu................................................................................................................................................5 2 Hello World.......................................................................................................................................6 2.1 Source Code......................................................................................................................................6 2.2 Compilation and Emulation...............................................................................................................8 2.3 Details...............................................................................................................................................9 -

Java (Programming Langua a (Programming Language)
Java (programming language) From Wikipedia, the free encyclopedialopedia "Java language" redirects here. For the natural language from the Indonesian island of Java, see Javanese language. Not to be confused with JavaScript. Java multi-paradigm: object-oriented, structured, imperative, Paradigm(s) functional, generic, reflective, concurrent James Gosling and Designed by Sun Microsystems Developer Oracle Corporation Appeared in 1995[1] Java Standard Edition 8 Update Stable release 5 (1.8.0_5) / April 15, 2014; 2 months ago Static, strong, safe, nominative, Typing discipline manifest Major OpenJDK, many others implementations Dialects Generic Java, Pizza Ada 83, C++, C#,[2] Eiffel,[3] Generic Java, Mesa,[4] Modula- Influenced by 3,[5] Oberon,[6] Objective-C,[7] UCSD Pascal,[8][9] Smalltalk Ada 2005, BeanShell, C#, Clojure, D, ECMAScript, Influenced Groovy, J#, JavaScript, Kotlin, PHP, Python, Scala, Seed7, Vala Implementation C and C++ language OS Cross-platform (multi-platform) GNU General Public License, License Java CommuniCommunity Process Filename .java , .class, .jar extension(s) Website For Java Developers Java Programming at Wikibooks Java is a computer programming language that is concurrent, class-based, object-oriented, and specifically designed to have as few impimplementation dependencies as possible.ble. It is intended to let application developers "write once, run ananywhere" (WORA), meaning that code that runs on one platform does not need to be recompiled to rurun on another. Java applications ns are typically compiled to bytecode (class file) that can run on anany Java virtual machine (JVM)) regardless of computer architecture. Java is, as of 2014, one of tthe most popular programming ng languages in use, particularly for client-server web applications, witwith a reported 9 million developers.[10][11] Java was originallyy developed by James Gosling at Sun Microsystems (which has since merged into Oracle Corporation) and released in 1995 as a core component of Sun Microsystems'Micros Java platform. -

The Java® Language Specification Java SE 8 Edition
The Java® Language Specification Java SE 8 Edition James Gosling Bill Joy Guy Steele Gilad Bracha Alex Buckley 2015-02-13 Specification: JSR-337 Java® SE 8 Release Contents ("Specification") Version: 8 Status: Maintenance Release Release: March 2015 Copyright © 1997, 2015, Oracle America, Inc. and/or its affiliates. 500 Oracle Parkway, Redwood City, California 94065, U.S.A. All rights reserved. Oracle and Java are registered trademarks of Oracle and/or its affiliates. Other names may be trademarks of their respective owners. The Specification provided herein is provided to you only under the Limited License Grant included herein as Appendix A. Please see Appendix A, Limited License Grant. To Maurizio, with deepest thanks. Table of Contents Preface to the Java SE 8 Edition xix 1 Introduction 1 1.1 Organization of the Specification 2 1.2 Example Programs 6 1.3 Notation 6 1.4 Relationship to Predefined Classes and Interfaces 7 1.5 Feedback 7 1.6 References 7 2 Grammars 9 2.1 Context-Free Grammars 9 2.2 The Lexical Grammar 9 2.3 The Syntactic Grammar 10 2.4 Grammar Notation 10 3 Lexical Structure 15 3.1 Unicode 15 3.2 Lexical Translations 16 3.3 Unicode Escapes 17 3.4 Line Terminators 19 3.5 Input Elements and Tokens 19 3.6 White Space 20 3.7 Comments 21 3.8 Identifiers 22 3.9 Keywords 24 3.10 Literals 24 3.10.1 Integer Literals 25 3.10.2 Floating-Point Literals 31 3.10.3 Boolean Literals 34 3.10.4 Character Literals 34 3.10.5 String Literals 35 3.10.6 Escape Sequences for Character and String Literals 37 3.10.7 The Null Literal 38 3.11 Separators -

Building Useful Program Analysis Tools Using an Extensible Java Compiler
Building Useful Program Analysis Tools Using an Extensible Java Compiler Edward Aftandilian, Raluca Sauciuc Siddharth Priya, Sundaresan Krishnan Google, Inc. Google, Inc. Mountain View, CA, USA Hyderabad, India feaftan, [email protected] fsiddharth, [email protected] Abstract—Large software companies need customized tools a specific task, but they fail for several reasons. First, ad- to manage their source code. These tools are often built in hoc program analysis tools are often brittle and break on an ad-hoc fashion, using brittle technologies such as regular uncommon-but-valid code patterns. Second, simple ad-hoc expressions and home-grown parsers. Changes in the language cause the tools to break. More importantly, these ad-hoc tools tools don’t provide sufficient information to perform many often do not support uncommon-but-valid code code patterns. non-trivial analyses, including refactorings. Type and symbol We report our experiences building source-code analysis information is especially useful, but amounts to writing a tools at Google on top of a third-party, open-source, extensible type-checker. Finally, more sophisticated program analysis compiler. We describe three tools in use on our Java codebase. tools are expensive to create and maintain, especially as the The first, Strict Java Dependencies, enforces our dependency target language evolves. policy in order to reduce JAR file sizes and testing load. The second, error-prone, adds new error checks to the compilation In this paper, we present our experience building special- process and automates repair of those errors at a whole- purpose tools on top of the the piece of software in our codebase scale. -

SUBJECT-COMPUTER CLASS-12 CHAPTER 9 – Compiling and Running Java Programs
SUBJECT-COMPUTER CLASS-12 CHAPTER 9 – Compiling and Running Java Programs Introduction to Java programming JAVA was developed by Sun Microsystems Inc in 1991, later acquired by Oracle Corporation. It was developed by James Gosling and Patrick Naughton. It is a simple programming language. Writing, compiling and debugging a program is easy in java. It helps to create modular programs and reusable code. Bytecode javac compiler of JDK compiles the java source code into bytecode so that it can be executed by JVM. The bytecode is saved in a .class file by compiler. Java Virtual Machine (JVM) This is generally referred as JVM. Before, we discuss about JVM lets see the phases of program execution. Phases are as follows: we write the program, then we compile the program and at last we run the program. 1) Writing of the program is of course done by java programmer. 2) Compilation of program is done by javac compiler, javac is the primary java compiler included in java development kit (JDK). It takes java program as input and generates java bytecode as output. 3) In third phase, JVM executes the bytecode generated by compiler. This is called program run phase. So, now that we understood that the primary function of JVM is to execute the bytecode produced by compiler. Characteristics of Java Simple Java is very easy to learn, and its syntax is simple, clean and easy to understand. Multi-threaded Multithreading capabilities come built right into the Java language. This means it is possible to build highly interactive and responsive apps with a number of concurrent threads of activity. -

Coqjvm: an Executable Specification of the Java Virtual Machine Using
CoqJVM: An Executable Specification of the Java Virtual Machine using Dependent Types Robert Atkey LFCS, School of Informatics, University of Edinburgh Mayfield Rd, Edinburgh EH9 3JZ, UK [email protected] Abstract. We describe an executable specification of the Java Virtual Machine (JVM) within the Coq proof assistant. The principal features of the development are that it is executable, meaning that it can be tested against a real JVM to gain confidence in the correctness of the specification; and that it has been written with heavy use of dependent types, this is both to structure the model in a useful way, and to constrain the model to prevent spurious partiality. We describe the structure of the formalisation and the way in which we have used dependent types. 1 Introduction Large scale formalisations of programming languages and systems in mechanised theorem provers have recently become popular [4–6, 9]. In this paper, we describe a formalisation of the Java virtual machine (JVM) [8] in the Coq proof assistant [11]. The principal features of this formalisation are that it is executable, meaning that a purely functional JVM can be extracted from the Coq development and – with some O’Caml glue code – executed on real Java bytecode output from the Java compiler; and that it is structured using dependent types. The motivation for this development is to act as a basis for certified consumer- side Proof-Carrying Code (PCC) [12]. We aim to prove the soundness of program logics and correctness of proof checkers against the model, and extract the proof checkers to produce certified stand-alone tools. -

Chapter 9: Java
,ch09.6595 Page 159 Friday, March 25, 2005 2:47 PM Chapter 9 CHAPTER 9 Java Many Java developers like Integrated Development Environments (IDEs) such as Eclipse. Given such well-known alternatives as Java IDEs and Ant, readers could well ask why they should even think of using make on Java projects. This chapter explores the value of make in these situations; in particular, it presents a generalized makefile that can be dropped into just about any Java project with minimal modification and carry out all the standard rebuilding tasks. Using make with Java raises several issues and introduces some opportunities. This is primarily due to three factors: the Java compiler, javac, is extremely fast; the stan- dard Java compiler supports the @filename syntax for reading “command-line param- eters” from a file; and if a Java package is specified, the Java language specifies a path to the .class file. Standard Java compilers are very fast. This is primarily due to the way the import directive works. Similar to a #include in C, this directive is used to allow access to externally defined symbols. However, rather than rereading source code, which then needs to be reparsed and analyzed, Java reads the class files directly. Because the symbols in a class file cannot change during the compilation process, the class files are cached by the compiler. In even medium-sized projects, this means the Java com- piler can avoid rereading, parsing, and analyzing literally millions of lines of code compared with C. A more modest performance improvement is due to the bare mini- mum of optimization performed by most Java compilers. -

Lecture 1: Introduction to Java®
Lecture 1: Introduction to Java MIT-AITI Kenya 2005 1 Lecture Outline • What a computer program is • How to write a computer program • The disadvantages and advantages of using Java • How a program that you write in Java is changed into a form that your computer can understand • Sample Java code and comments MIT-Africa Internet Technology Initiative ©2005 2 Computer Program vs. Food Recipe Food Recipe Computer Program A chef writes a set of A programmer writes a set of instructions called a recipe instructions called a program The recipe requires specific The program requires specific ingredients inputs The cook follows the The computer follows the instructions step-by-step instructions step-by-step The food will vary depending on The output will vary depending the amount of ingredients and on the values of the inputs and the cook the computer MIT-Africa Internet Technology Initiative ©2005 3 Recipe and Program Examples Student’s Student’s Ingredient # 1 Ingredient # 2 Name Grade Recipe Program Dinner “Bilha got an A on the exam!” MIT-Africa Internet Technology Initiative ©2005 4 What is a computer program? • For a computer to be able to perform specific tasks (i.e. print what grade a student got on an exam), it must be given instructions to do the task • The set of instructions that tells the computer to perform specific tasks is known as a computer program MIT-Africa Internet Technology Initiative ©2005 5 Writing Computer Programs • We write computer programs (i.e. a set of instructions) in programming languages such as C, Pascal, and -
Metaprogramming: Interpretaaon Interpreters
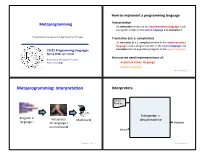
How to implement a programming language Metaprogramming InterpretaAon An interpreter wriDen in the implementaAon language reads a program wriDen in the source language and evaluates it. These slides borrow heavily from Ben Wood’s Fall ‘15 slides. TranslaAon (a.k.a. compilaAon) An translator (a.k.a. compiler) wriDen in the implementaAon language reads a program wriDen in the source language and CS251 Programming Languages translates it to an equivalent program in the target language. Spring 2018, Lyn Turbak But now we need implementaAons of: Department of Computer Science Wellesley College implementaAon language target language Metaprogramming 2 Metaprogramming: InterpretaAon Interpreters Source Program Interpreter = Program in Interpreter Machine M virtual machine language L for language L Output on machine M Data Metaprogramming 3 Metaprogramming 4 Metaprogramming: TranslaAon Compiler C Source x86 Target Program C Compiler Program if (x == 0) { cmp (1000), $0 Program in Program in x = x + 1; bne L language A } add (1000), $1 A to B translator language B ... L: ... x86 Target Program x86 computer Output Interpreter Machine M Thanks to Ben Wood for these for language B Data and following pictures on machine M Metaprogramming 5 Metaprogramming 6 Interpreters vs Compilers Java Compiler Interpreters No work ahead of Lme Source Target Incremental Program Java Compiler Program maybe inefficient if (x == 0) { load 0 Compilers x = x + 1; ifne L } load 0 All work ahead of Lme ... inc See whole program (or more of program) store 0 Time and resources for analysis and opLmizaLon L: ... (compare compiled C to compiled Java) Metaprogramming 7 Metaprogramming 8 Compilers... whose output is interpreted Interpreters.. -

1 Compiling Java Programs
CS 61B P. N. Hilfinger Basic Compilation: javac, gcc, g++ 1 Compiling Java Programs [The discussion in this section applies to Java 1.2 tools from Sun Microsystems. Tools from other manufac- turers and earlier tools from Sun differ in various details.] Programming languages do not exist in a vacuum; any actual programming done in any language one does within a programming environment that comprises the various programs, libraries, editors, debuggers, and other tools needed to actually convert program text into action. The Scheme environment that you used in CS61A was particularly simple. It provided a component called the reader, which read in Scheme-program text from files or command lines and converted it into internal Scheme data structures. Then a component called the interpreter operated on these translated pro- grams or statements, performing the actions they denoted. You probably weren’t much aware of the reader; it doesn’t amount to much because of Scheme’s very simple syntax. Java’s more complex syntax and its static type structure (as discussed in lecture) require that you be a bit more aware of the reader—or compiler, as it is called in the context of Java and most other “production” programming languages. The Java compiler supplied by Sun Microsystems is a program called javac on our systems. You first prepare programs in files (called source files) using any appropriate text editor (Emacs, for example), giving them names that end in ‘.java’. Next you compile them with the java compiler to create new, translated files, called class files, one for each class, with names ending in ‘.class’. -

Java Virtual Machine Guide
Java Platform, Standard Edition Java Virtual Machine Guide Release 14 F23572-02 May 2021 Java Platform, Standard Edition Java Virtual Machine Guide, Release 14 F23572-02 Copyright © 1993, 2021, Oracle and/or its affiliates. This software and related documentation are provided under a license agreement containing restrictions on use and disclosure and are protected by intellectual property laws. Except as expressly permitted in your license agreement or allowed by law, you may not use, copy, reproduce, translate, broadcast, modify, license, transmit, distribute, exhibit, perform, publish, or display any part, in any form, or by any means. Reverse engineering, disassembly, or decompilation of this software, unless required by law for interoperability, is prohibited. The information contained herein is subject to change without notice and is not warranted to be error-free. If you find any errors, please report them to us in writing. If this is software or related documentation that is delivered to the U.S. Government or anyone licensing it on behalf of the U.S. Government, then the following notice is applicable: U.S. GOVERNMENT END USERS: Oracle programs (including any operating system, integrated software, any programs embedded, installed or activated on delivered hardware, and modifications of such programs) and Oracle computer documentation or other Oracle data delivered to or accessed by U.S. Government end users are "commercial computer software" or "commercial computer software documentation" pursuant to the applicable Federal Acquisition -

Java (Software Platform) from Wikipedia, the Free Encyclopedia Not to Be Confused with Javascript
Java (software platform) From Wikipedia, the free encyclopedia Not to be confused with JavaScript. This article may require copy editing for grammar, style, cohesion, tone , or spelling. You can assist by editing it. (February 2016) Java (software platform) Dukesource125.gif The Java technology logo Original author(s) James Gosling, Sun Microsystems Developer(s) Oracle Corporation Initial release 23 January 1996; 20 years ago[1][2] Stable release 8 Update 73 (1.8.0_73) (February 5, 2016; 34 days ago) [±][3] Preview release 9 Build b90 (November 2, 2015; 4 months ago) [±][4] Written in Java, C++[5] Operating system Windows, Solaris, Linux, OS X[6] Platform Cross-platform Available in 30+ languages List of languages [show] Type Software platform License Freeware, mostly open-source,[8] with a few proprietary[9] compo nents[10] Website www.java.com Java is a set of computer software and specifications developed by Sun Microsyst ems, later acquired by Oracle Corporation, that provides a system for developing application software and deploying it in a cross-platform computing environment . Java is used in a wide variety of computing platforms from embedded devices an d mobile phones to enterprise servers and supercomputers. While less common, Jav a applets run in secure, sandboxed environments to provide many features of nati ve applications and can be embedded in HTML pages. Writing in the Java programming language is the primary way to produce code that will be deployed as byte code in a Java Virtual Machine (JVM); byte code compil ers are also available for other languages, including Ada, JavaScript, Python, a nd Ruby.