Finite Element Modelling of Sound Transmission Loss in Reflective Pipe
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Definition and Measurement of Sound Energy Level of a Transient Sound Source
J. Acoust. Soc. Jpn. (E) 8, 6 (1987) Definition and measurement of sound energy level of a transient sound source Hideki Tachibana,* Hiroo Yano,* and Koichi Yoshihisa** *Institute of Industrial Science , University of Tokyo, 7-22-1, Roppongi, Minato-ku, Tokyo, 106 Japan **Faculty of Science and Technology, Meijo University, 1-501, Shiogamaguti, Tenpaku-ku, Nagoya, 468 Japan (Received 1 May 1987) Concerning stationary sound sources, sound power level which describes the sound power radiated by a sound source is clearly defined. For its measuring methods, the sound pressure methods using free field, hemi-free field and diffuse field have been established, and they have been standardized in the international and national stan- dards. Further, the method of sound power measurement using the sound intensity technique has become popular. On the other hand, concerning transient sound sources such as impulsive and intermittent sound sources, the way of describing and measuring their acoustic outputs has not been established. In this paper, therefore, "sound energy level" which represents the total sound energy radiated by a single event of a transient sound source is first defined as contrasted with the sound power level. Subsequently, its measuring methods by two kinds of sound pressure method and sound intensity method are investigated theoretically and experimentally on referring to the methods of sound power level measurement. PACS number : 43. 50. Cb, 43. 50. Pn, 43. 50. Yw sources, the way of describing and measuring their 1. INTRODUCTION acoustic outputs has not been established. In noise control problems, it is essential to obtain In this paper, "sound energy level" which repre- the information regarding the noise sources. -

Sound Power Measurement What Is Sound, Sound Pressure and Sound Pressure Level?
www.dewesoft.com - Copyright © 2000 - 2021 Dewesoft d.o.o., all rights reserved. Sound power measurement What is Sound, Sound Pressure and Sound Pressure Level? Sound is actually a pressure wave - a vibration that propagates as a mechanical wave of pressure and displacement. Sound propagates through compressible media such as air, water, and solids as longitudinal waves and also as transverse waves in solids. The sound waves are generated by a sound source (vibrating diaphragm or a stereo speaker). The sound source creates vibrations in the surrounding medium. As the source continues to vibrate the medium, the vibrations propagate away from the source at the speed of sound and are forming the sound wave. At a fixed distance from the sound source, the pressure, velocity, and displacement of the medium vary in time. Compression Refraction Direction of travel Wavelength, λ Movement of air molecules Sound pressure Sound pressure or acoustic pressure is the local pressure deviation from the ambient (average, or equilibrium) atmospheric pressure, caused by a sound wave. In air the sound pressure can be measured using a microphone, and in water with a hydrophone. The SI unit for sound pressure p is the pascal (symbol: Pa). 1 Sound pressure level Sound pressure level (SPL) or sound level is a logarithmic measure of the effective sound pressure of a sound relative to a reference value. It is measured in decibels (dB) above a standard reference level. The standard reference sound pressure in the air or other gases is 20 µPa, which is usually considered the threshold of human hearing (at 1 kHz). -

Analytical, Numerical and Experimental Calculation of Sound Transmission Loss Characteristics of Single Walled Muffler Shells
1 Analytical, Numerical and Experimental calculation of sound transmission loss characteristics of single walled muffler shells A thesis submitted to the Division of Graduate Studies and Research of the University of Cincinnati in partial fulfillment of the requirements for the degree of MASTER OF SCIENCE In the Department of Mechanical Engineering of the College of Engineering May 2007 by John George B. E., Regional Engineering College, Surat, India, 1995 M. E., Regional Engineering College, Trichy, India, 1997 Committee Chair: Dr. Jay Kim 2 Abstract Accurate prediction of sound radiation characteristics from muffler shells is of significant importance in automotive exhaust system design. The most commonly used parameter to evaluate the sound radiation characteristic of a structure is transmission loss (TL). Many tools are available to simulate the transmission loss characteristic of structures and they vary in terms of complexity and inherent assumptions. MATLAB based analytical models are very valuable in the early part of the design cycle to estimate design alternatives quickly, as they are very simple to use and could be used by the design engineers themselves. However the analytical models are generally limited to simple shapes and cannot handle more complex contours as the geometry evolves during the design process. Numerical models based on Finite Element Method (FEM) and Boundary Element Method (BEM) requires expert knowledge and is more suited to handle complex muffler configurations in the latter part of the design phase. The subject of this study is to simulate TL characteristics from muffler shells utilizing commercially available FEM/BEM tools (NASTRAN and SYSNOISE, in this study) and MATLAB based analytical model. -

Sound Transmission Loss Test AS-TL1765
Acoustical Surfaces, Inc. Acoustical Surfaces, Inc. We identify and SOUNDPROOFING, ACOUSTICS, NOISE & VIBRATION CONTROL SPECIALISTS 123 Columbia Court North = Suite 201 = Chaska, MN 55318 (952) 448-5300 = Fax (952) 448-2613 = (800) 448-0121 Email: [email protected] Your Noise Problems Visit our Website: www.acousticalsurfaces.com Sound Transmission Obscuring Products Soundproofing, Acoustics, Noise & Vibration Control Specialists ™ We Identify and S.T.O.P. Your Noise Problems ACOUSTIC SYSTEMS ACOUSTICAL RESEARCH FACILITY OFFICIAL LABORATORY REPORT AS-TL1765 Subject: Sound Transmission Loss Test Date: December 26, 2000 Contents: Transmission Loss Data, One-third Octave Bands Transmission Loss Data, Octave Bands Sound Transmission Class Rating Outdoor /Indoor Transmission Class Rating on Asymmetrical Staggered Metal Stud Wall Assembly w/Two Layers 5/8” FIRECODE Gypsum (Source Side), One Layer 5/8” FIRECODE Gypsum on RC-1 Channels (Receive Side), and R-19 UltraTouch Blue Insulation for Rendered by Manufacturer and released to Acoustical Surfaces 123 Columbia Court North Chaska, MN 55318 ACOUSTIC SYSTEMS ACOUSTICAL RESEARCH FACILITY is NVLAP-Accredited for this and other test procedures National Institute of Standards National Voluntary and Technology Laboratory Accreditation Program Certified copies of the Report carry a Raised Seal on every page. Reports may be reproduced freely if in full and without alteration. Results apply only to the unit tested and do not extend to other same or similar items. The NVLAP logo does not denote -

Sound Waves Sound Waves • Speed of Sound • Acoustic Pressure • Acoustic Impedance • Decibel Scale • Reflection of Sound Waves • Doppler Effect
In this lecture • Sound waves Sound Waves • Speed of sound • Acoustic Pressure • Acoustic Impedance • Decibel Scale • Reflection of sound waves • Doppler effect Sound Waves (Longitudinal Waves) Sound Range Frequency Source, Direction of propagation Vibrating surface Audible Range 15 – 20,000Hz Propagation Child’’s hearing 15 – 40,000Hz of zones of Male voice 100 – 1500Hz alternating ------+ + + + + compression Female voice 150 – 2500Hz and Middle C 262Hz rarefaction Concert A 440Hz Pressure Bat sounds 50,000 – 200,000Hz Wavelength, λ Medical US 2.5 - 40 MHz Propagation Speed = number of cycles per second X wavelength Max sound freq. 600 MHz c = f λ B Speed of Sound c = Sound Particle Velocity ρ • Speed at which longitudinal displacement of • Velocity, v, of the particles in the particles propagates through medium material as they oscillate to and fro • Speed governed by mechanical properties of c medium v • Stiffer materials have a greater Bulk modulus and therefore a higher speed of sound • Typically several tens of mms-1 1 Acoustic Pressure Acoustic Impedance • Pressure, p, caused by the pressure changes • Pressure, p, is applied to a molecule it induced in the material by the sound energy will exert pressure the adjacent molecule, which exerts pressure on its c adjacent molecule. P0 P • It is this sequence that causes pressure to propagate through medium. • p= P-P0 , (where P0 is normal pressure) • Typically several tens of kPa Acoustic Impedance Acoustic Impedance • Acoustic pressure increases with particle velocity, v, but also depends -

Aircraft Noise (Excerpt from the Oakland International Airport Master Plan Update – 2006)
Aircraft Noise (Excerpt from the Oakland International Airport Master Plan Update – 2006) Background This report presents background information on the characteristics of noise. Noise analyses involve the use of technical terms that are used to describe aviation noise. This section provides an overview of the metrics and methodologies used to assess the effects of noise. Characteristics of Sound Sound Level and Frequency — Sound can be technically described in terms of the sound pressure (amplitude) and frequency (similar to pitch). Sound pressure is a direct measure of the magnitude of a sound without consideration for other factors that may influence its perception. The range of sound pressures that occur in the environment is so large that it is convenient to express these pressures as sound pressure levels on a logarithmic scale that compresses the wide range of sound pressures to a more usable range of numbers. The standard unit of measurement of sound is the Decibel (dB) that describes the pressure of a sound relative to a reference pressure. The frequency (pitch) of a sound is expressed as Hertz (Hz) or cycles per second. The normal audible frequency for young adults is 20 Hz to 20,000 Hz. Community noise, including aircraft and motor vehicles, typically ranges between 50 Hz and 5,000 Hz. The human ear is not equally sensitive to all frequencies, with some frequencies judged to be louder for a given signal than others. See Figure 6.2. As a result of this, various methods of frequency weighting have been developed. The most common weighting is the A-weighted noise curve (dBA). -
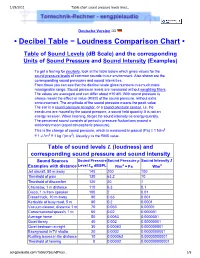
Table Chart Sound Pressure Levels Level Sound Pressure
1/29/2011 Table chart sound pressure levels level… Deutsche Version • Decibel Table − Loudness Comparison Chart • Table of Sound Levels (dB Scale) and the corresponding Units of Sound Pressure and Sound Intensity (Examples) To get a feeling for decibels, look at the table below which gives values for the sound pressure levels of common sounds in our environment. Also shown are the corresponding sound pressures and sound intensities. From these you can see that the decibel scale gives numbers in a much more manageable range. Sound pressure levels are measured without weighting filters. The values are averaged and can differ about ±10 dB. With sound pressure is always meant the effective value (RMS) of the sound pressure, without extra announcement. The amplitude of the sound pressure means the peak value. The ear is a sound pressure receptor, or a sound pressure sensor, i.e. the ear-drums are moved by the sound pressure, a sound field quantity. It is not an energy receiver. When listening, forget the sound intensity as energy quantity. The perceived sound consists of periodic pressure fluctuations around a stationary mean (equal atmospheric pressure). This is the change of sound pressure, which is measured in pascal (Pa) ≡ 1 N/m2 ≡ 1 J / m3 ≡ 1 kg / (m·s2). Usually p is the RMS value. Table of sound levels L (loudness) and corresponding sound pressure and sound intensity Sound Sources Sound PressureSound Pressure p Sound Intensity I Examples with distance Level Lp dBSPL N/m2 = Pa W/m2 Jet aircraft, 50 m away 140 200 100 Threshold of pain -

Echo Time Spreading and the Definition of Transmission Loss for Broadband Active Sonar
Paper Number 97, Proceedings of ACOUSTICS 2011 2-4 November 2011, Gold Coast, Australia Echo time spreading and the definition of transmission loss for broadband active sonar Z. Y. Zhang Defence Science and Technology Organisation P.O. Box 1500, Edinburgh, SA 5111, Australia ABSTRACT In active sonar, the echo from a target is the convolution of the source waveform with the impulse responses of the target and the propagation channel. The transmitted source waveform is generally known and replica-correlation is used to increase the signal gain. This process is also called pulse compression because for broadband pulses the re- sulting correlation functions are impulse-like. The echo after replica-correlation may be regarded as equivalent to that received by transmitting the impulsive auto-correlation function of the source waveform. The echo energy is spread out in time due to different time-delays of the multipath propagation and from the scattering process from the target. Time spreading leads to a reduction in the peak power of the echo in comparison with that which would be obtained had all multipaths overlapped in time-delay. Therefore, in contrast to passive sonar where all energies from all sig- nificant multipaths are included, the concept of transmission losses in the active sonar equation needs to be handled with care when performing sonar performance modelling. We show modelled examples of echo time spreading for a baseline case from an international benchmarking workshop. INTRODUCTION ECHO MODELLING ISSUES The performance of an active sonar system is often illustrated In a sound channel, the transmitted pulse generally splits into by the power (or energy) budget afforded by a separable form multipath arrivals with different propagation angles and of the sonar equation, such as the following, travel times that ensonify the target, which scatters and re- radiates each arrival to more multipath arrivals at the re- SE = EL – [(NL – AGN) ⊕ RL] + MG – DT (1) ceiver. -

SOUND ATTENUATION in DUCTS
SOUND ATTENUATION in DUCTS 14.1 SOUND PROPAGATION THROUGH DUCTS When sound propagates through a duct system it encounters various elements that provide sound attenuation. These are lumped into general categories, including ducts, elbows, plenums, branches, silencers, end effects, and so forth. Other elements such as tuned stubs and Helmholtz resonators can also produce losses; however, they rarely are encountered in practice. Each of these elements attenuates sound by a quantifiable amount, through mechanisms that are relatively well understood and lead to a predictable result. Theory of Propagation in Ducts with Losses Noise generated by fans and other devices is transmitted, often without appreciable loss, from the source down an unlined duct and into an occupied space. Since ducts confine the naturally expanding acoustical wave, little attenuation occurs due to geometric spreading. So efficient are pipes and ducts in delivering a sound signal in its original form, that they are still used on board ships as a conduit for communications. To obtain appreciable attenuation, we must apply materials such as a fiberglass liner to the duct’s inner surfaces to create a loss mechanism by absorbing sound incident upon it. In Chapt. 8, we examined the propagation of sound waves in ducts without resistance and the phenomenon of cutoff. Recall that cutoff does not imply that all sound energy is prevented from being transmitted along a duct. Rather, it means that only particular waveforms propagate at certain frequencies. Below the cutoff frequency only plane waves are allowed, and above that frequency, only multimodal waves propagate. In analyzing sound propagation in ducts it is customary to simplify the problem into one having only two dimensions. -

2015 Standard for Sound Rating and Sound Transmission Loss of Packaged Terminal Equipment
ANSI/AHRI Standard 300 2015 Standard for Sound Rating and Sound Transmission Loss of Packaged Terminal Equipment Approved by ANSI on July 8, 2016 IMPORTANT SAFETY DISCLAIMER AHRI does not set safety standards and does not certify or guarantee the safety of any products, components or systems designed, tested, rated, installed or operated in accordance with this standard/guideline. It is strongly recommended that products be designed, constructed, assembled, installed and operated in accordance with nationally recognized safety standards and code requirements appropriate for products covered by this standard/guideline. AHRI uses its best efforts to develop standards/guidelines employing state-of-the-art and accepted industry practices. AHRI does not certify or guarantee that any tests conducted under its standards/guidelines will be non-hazardous or free from risk. Note: This standard supersedes AHRI Standard 300-2008. Note: This version of the standard differs from the 2008 version of the standard in the following: This standard references the sound intensity test method defined in ANSI/AHRI Standard 230, as an alternate method of test to the reverberation room test method defined in ANSI/AHRI Standard 220 for determination of sound power ratings. Price $10.00 (M) $20.00 (NM) ©Copyright 2015, by Air-Conditioning, Heating, and Refrigeration Institute Printed in U.S.A. Registered United States Patent and Trademark Office TABLE OF CONTENTS SECTION PAGE Section 1. Purpose .......................................................................................................................................... -

M-046 Fundamentals of Acoustics and Vibrations
M‐046 Fundamentals of Acoustics and Vibrations Instructor: J. Paul Guyer, P.E., R.A. Course ID: M‐046 PDH Hours: 2 PDH PDH Star | T / F: (833) PDH‐STAR (734‐7827) | E: [email protected] An Introduction to the Fundamentals of Acoustics and Vibrations nd 2 Edition J. Paul Guyer, P.E., R.A. Editor Paul Guyer is a registered civil engineer, mechanical engineer, fire protection engineer, and architect with over 35 years of experience in the design of buildings and related infrastructure. For an additional 9 years he was a principal staff advisor to the California Legislature. He is a graduate of Stanford University and has held numerous national, state and local offices with the American Society of Civil Engineers, Architectural Engineering Institute and National Society of Professional Engineers. He is a Fellow of ASCE, AEI and CABE (U.K.). An Introduction to the Fundamentals of Acoustics and Vibrations 2nd Edition J. Paul Guyer, P.E., R.A. Editor The Clubhouse Press El Macero, California CONTENTS 1. INTRODUCTION 2. DECIBELS 3. SOUND PRESSURE LEVEL 4. SOUND POWER LEVEL 5. SOUND INTENSITY LEVEL 6. VIBRATION LEVELS 7. FREQUENCY 8. TEMPORAL VARIATIONS 9. SPEED OF SOUND AND WAVELENGTH 10. LOUDNESS 11. VIBRATION TRANSMISSIBILITY 12. VIBRATION ISOLATION EFFECTIVENESS (This publication is adapted from the Unified Facilities Criteria of the United States government which are in the public domain, have been authorized for unlimited distribution, and are not copyrighted.) 1. INTRODUCTION 1.1 THIS DISCUSSION presents the basic quantities used to describe acoustical properties. For the purposes of the material contained in this document perceptible acoustical sensations can be generally classified into two broad categories, these are: Sound. -

Sound Intensity Measurement
This booklet sets out to explain the fundamentals of sound intensity measurement. Both theory and applica- tions will be covered. Although the booklet is intended as a basic introduction, some knowledge of sound pres- sure measurement is assumed. If you are unfamiliar with this subject, you may wish to consult our companion booklet "Measuring Sound". See page See page Introduction ........................................................................ 2 Spatial Averaging ...…......................................................... 15 Sound Pressure and Sound Power................................... 3 What about Background Noise? ....................................... 16 What is Sound Intensity? .................................................. 4 Noise Source Ranking ........................................................ 17 Why Measure Sound Intensity? ........................................ 5 Intensity Mapping .............................................…......... 18-19 Sound Fields ................................................................... 6-7 Applications in Building Acoustics .................................. 20 Pressure and Particle Velocity .......................................... 8 Instrumentation .................................................................. 21 How is Sound Intensity Measured? …......................... 9-10 Making Measurements ......................................…........ 22-23 The Sound Intensity Probe .............................................. 11 Further Applications and Advanced