DOCSLIB.ORG

Chapter 4: Solar Resource SOLUTIONS Gmasters

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Chapter 4: Solar Resource SOLUTIONS Gmasters Chapter 4: Solar Resource SOLUTIONS Chapter 4: Problems ________________________________________________________ 4.1 Consider the design of a “light shelf” for the south side of an office building locateD at a site with latitude 30o. The idea is that the light shelf should help Keep Direct sunlight from entering the office. It also bounces light up onto the ceiling to Distribute natural Daylight more uniformly into the office. o Upper LATITUDE 21.5 window 2 ft Light shelf 4 ft X1 X2 Lower window Not allowed S Figure P4.X As shown, the winDow Directly above the light shelf is 2-feet high and the window directly below is 4-ft. What shoulD the Dimensions X1 and X2 be to be sure that no direct sunlight ever enters the space at solar noon? SOLN: The worst day will be at the winter solstice when the sun is lowest in the sky, at which point the declination is -23.45o. From (4.7) the noon altituDe angle of the sun is o βΝ = 90 – L + δ = 90 - 30 - 23.45 = 36.55 36.55o o! 2 ft 45 2 X1 = o = 2.7 ft X2! tan 36.55 X21 !ft 4 ft 4 ft 4 X = = 5.4 ft 2 tan 36.55o S 4.2 Rows of buildings with photovoltaics covering vertical south-facing walls need to have adequate spacing to assure one building doesn't shade the collectors on another. gmasters Pg.4. 1 2/7/13 Chapter 4: Solar Resource SOLUTIONS !"#$%"$&'()*%+$,-./--%$01$(2$(%)$3$425$For$no$shading$between$8$am$and$4$pm,$d/H$≥$?$)67$8$9$ PVs$ H S d a. Using the shadow diagram for 30oN in AppenDix F, roughly what ratio of separation distance (d) to building height (H) would assure no shading anytime between 8 am anD 4 pm? b. If the spacing is such that d = H, During what months will the rear builDing receive full solar exposure. a. SOLN: 8 am anD 4 pm are just about 3 squares back, so with the peg being H, that means the separation D is about 3 H… D/H ≥ 3. (or, more accurately, d/H ≥ 2.8) b. SOLN: Looks like full sun for all of spring anD summer, but shaDing begins in October and runs into February . 4.3 Consider the challenge of designing an overhang to help shade a south-facing, sliding-glass patio Door. You woulD liKe to shaDe the glass in the summer to help control air-conditioning loads, and you woulD also like the glass to get full sun in the winter to help proviDe passive solar heating of the home. Suppose the slider has a height of 6.5 ft, the interior ceiling height is 8 ft, and the local latitude is 40o. a. What should be the overhang projection P to shade the entire window at solar noon during the solstice in June? gmasters Pg.4. 2 2/7/13 Chapter 4: Solar Resource SOLUTIONS b. With that overhang, where would the shade line, Y, be at solar noon on the winter solstice? P" βN" Y" 8)*"""6.5"*" South" Figure P4.X a. SOLN: To shade the window in June o Summer solstice βN = 90 − L + δ = 90 − 40 + 23.45 = 73.45 Y 8 P = = o = 2.377 ft tanβN tan 73.45 b. SOLN: In winter, when you want the sun, the shade line will be at Winter solstice β = 90 − 40 − 23.45 = 26.55o N o Y = P tanβN = 2.377 tan26.55 = 1.188 ft So, the shade line is 8 ft - 1.188 ft = 6.8 ft above the floor, so the entire window is in the sun. c. The shadow distance Y for a south-facing window when it is not solar noon is given by P tanβ Y = cosφS Will the bottom of the shadow line designed for solar noon still shade the window at 10 am? SOLN: 10:00 am is 2 h before solar noon, so H = 2h x 15o/h = 30o. From (4.8) sinβ = cos L cosδ cos H + sin L sinδ = cos 40 ⋅cos23.45 ⋅cos 30 + sin 40 ⋅sin23.45 β = 59.82o From (4.9) cosδ sin H cos23.45 ⋅sin 30 sinφ = = = 0.912 S cosβ cos59.82 o φS = 65.846 From the above equation gmasters Pg.4. 3 2/7/13 Chapter 4: Solar Resource SOLUTIONS P tanβ 2.377 tan59.82 Y = = = 9.99 ft cosφS cos65.846 So, the shadow still covers the window (ignoring edge effects). In fact, it will be shadeD all day long so designing for solar noon is a gooD strategy. 4.4 Suppose you are concerneD about how much shaDing a tree will cause for a proposeD photovoltaic system. StanDing at the site with your compass and plumb bob, you estimate the altituDe angle of the top of the tree to be about 30o anD the wiDth of the tree to have azimuth angles that range from about 30o to 45o west of south. Your site is at latitude 32o. Using a sun path diagram (AppenDix C), describe the shaDing problem the tree will pose (approximate shaDeD times each month). SOLN: The tree shaDes the site from roughly 2 pm to 3 pm from roughly miD-November through miD-January. 4.5 Suppose you are concerned about a tall thin tree located 100 ft from a proposeD PV site. You Don’t have a compass or protractor anD plumb bob, but you do notice that an hour before solar noon on June 21 it casts a 30 ft shadow directly toward your site. Your latitude is 32o N. a. How tall is the tree? b. What is its azimuth angle with respect to your site? c. Using an appropriate sun path Diagram from AppenDix C, roughly what are the first and last days in the year when the shadow will land on the site? SOLN: a. It is the summer solstice so δ = 23.45o and it is an hour before solar noon so the hour angle is 15o. From (4.8) the altitude angle of the sun is gmasters Pg.4. 4 2/7/13 Chapter 4: Solar Resource SOLUTIONS sinβ = cos L cosδ cos H + sin L sinδ = cos 32cos23.45cos15 + sin 32sin23.45 = 0.962 β = 74.23o From h/30 = tan 74.23o the tree height is h = 30 tan 74.23o = 106 ft b. From (4.9) the azimuth angle of the tree is ⎛ cosδ sin H ⎞ ⎛ cos23.45sin15⎞ o φS = Asin = Asin⎜ ⎟ = 60.9 ⎝⎜ cosβ ⎠⎟ ⎝ cos 74.23 ⎠ c. The altitude angle of the tree relative to the site is β = Atan(106/100) = 46.7o From the sun path Diagram for 32o and using the altitude of the tree as 46.7o anD the azimuth 60.6o it looKs liKe the site is shaDeD briefly each Day from early September to early April. S! 61o! PV! 106’! PV! o 74.2o! 46.7 ! !0!!!!!!!!!!!!30’!!!!!!!!!!!!!!!!!100’! 4.6 Using Figure 4.18, what is the greatest Difference between local stanDarD time and solar time for the following locations? At approximately what Date woulD that occur? a. San Francisco, CA (longituDe 122o, Pacific Time Zone) b. Boston, MA (longituDe 71.1o, Eastern Time Zone) c. Boulder, CO (longitude 105.3o, Mountain Time Zone) d. Greenwich, England (longitude 0o, Local time meriDian 0o) SOLN: Using (4.14) ST – CT = 4(Local Meridian – Local Long) + E The extremes of the equation of time Emax ≈ +16.5 min arounD n = 303, or about October 30, anD Emin ≈ - 14.6 min arounD n = 44, or about February 13. Using time zones from Table 4.3: a. San Francisco: MAX = 4(120 – 122) + E = -8 –14.6 = -22.6 minutes arounD February 13 b. Boston: MAX = 4(75 – 71.1) + E = 15.6 + 16.5 = 32.1 minutes arounD October 30 c. Boulder: 4(105 – 105.3) + E = - 1.2 - 14.6 = -15.8 minutes arounD February 13 gmasters Pg.4. 5 2/7/13 Chapter 4: Solar Resource SOLUTIONS (check -1.2 + 16.5 = 15.3 arounD October 30… not quite as baD) d. Greenwich: MAX = 4(0 – 0) + E = 16.5 minutes arounD October 30 4.7 Calculate the following for (geometric) sunrise in Seattle, latitude 47.63o, longitude 122.33o W (in the Pacific Time Zone), on the summer solstice (June 21st). a. Find the azimuth angle of sunrise relative to due south. b. Find the time of sunrise expressed in solar time. c. Find the local time of sunrise. Compare it to the website http://aa.usno.navy.mil/data/docs/RS_OneDay.html. Why do they differ? SOLN: a. From (4.16) and (4.9) realizing β = 0 at sunrise: (4.16) cos H = − tan L tanδ = − tan 47.63tan23.45 = −0.4755 so H = 118.39o cosδ sin H cos23.45sin118.39 (4.9) sinφ = = = 0.807 S cosβ cos0 o o so φS could be either 53.81 or 180-53.81 = 126.19 Test this using (4.11) tanδ tan23.45 cos H = cos118.39 = −0.475 and = = 0.396 tan L tan 47.63 tanδ since cos H < then φ > 90 tan L S So the azimuth angle at sunrise is 126.19o toward the north-east (which is obvious from any sun path diagram). b. Sunrise can be found from the hour angle H 118.39o Sunrise = o = o = 7.893h = 7h 53.56min before solar noon 15 / h 15 / h That is, in solar time, Sunrise = 4:06.44 am.
Load more

Recommended publications
  • Capricious Suntime
    [Physics in daily life] I L.J.F. (Jo) Hermans - Leiden University, e Netherlands - [email protected] - DOI: 10.1051/epn/2011202 Capricious suntime t what time of the day does the sun reach its is that the solar time will gradually deviate from the time highest point, or culmination point, when on our watch. We expect this‘eccentricity effect’ to show a its position is exactly in the South? e ans - sine-like behaviour with a period of a year. A wer to this question is not so trivial. For ere is a second, even more important complication. It is one thing, it depends on our location within our time due to the fact that the rotational axis of the earth is not zone. For Berlin, which is near the Eastern end of the perpendicular to the ecliptic, but is tilted by about 23.5 Central European time zone, it may happen around degrees. is is, aer all, the cause of our seasons. To noon, whereas in Paris it may be close to 1 p.m. (we understand this ‘tilt effect’ we must realise that what mat - ignore the daylight saving ters for the deviation in time time which adds an extra is the variation of the sun’s hour in the summer). horizontal motion against But even for a fixed loca - the stellar background tion, the time at which the during the year. In mid- sun reaches its culmination summer and mid-winter, point varies throughout the when the sun reaches its year in a surprising way.
    [Show full text]
  • Solar Engineering Basics
    Solar Energy Fundamentals Course No: M04-018 Credit: 4 PDH Harlan H. Bengtson, PhD, P.E. Continuing Education and Development, Inc. 22 Stonewall Court Woodcliff Lake, NJ 07677 P: (877) 322-5800 [email protected] Solar Energy Fundamentals Harlan H. Bengtson, PhD, P.E. COURSE CONTENT 1. Introduction Solar energy travels from the sun to the earth in the form of electromagnetic radiation. In this course properties of electromagnetic radiation will be discussed and basic calculations for electromagnetic radiation will be described. Several solar position parameters will be discussed along with means of calculating values for them. The major methods by which solar radiation is converted into other useable forms of energy will be discussed briefly. Extraterrestrial solar radiation (that striking the earth’s outer atmosphere) will be discussed and means of estimating its value at a given location and time will be presented. Finally there will be a presentation of how to obtain values for the average monthly rate of solar radiation striking the surface of a typical solar collector, at a specified location in the United States for a given month. Numerous examples are included to illustrate the calculations and data retrieval methods presented. Image Credit: NOAA, Earth System Research Laboratory 1 • Be able to calculate wavelength if given frequency for specified electromagnetic radiation. • Be able to calculate frequency if given wavelength for specified electromagnetic radiation. • Know the meaning of absorbance, reflectance and transmittance as applied to a surface receiving electromagnetic radiation and be able to make calculations with those parameters. • Be able to obtain or calculate values for solar declination, solar hour angle, solar altitude angle, sunrise angle, and sunset angle.
    [Show full text]
  • Chapter Outline Thinking Ahead 4 EARTH, MOON, AND
    Chapter 4 Earth, Moon, and Sky 103 4 EARTH, MOON, AND SKY Figure 4.1 Southern Summer. As captured with a fish-eye lens aboard the Atlantis Space Shuttle on December 9, 1993, Earth hangs above the Hubble Space Telescope as it is repaired. The reddish continent is Australia, its size and shape distorted by the special lens. Because the seasons in the Southern Hemisphere are opposite those in the Northern Hemisphere, it is summer in Australia on this December day. (credit: modification of work by NASA) Chapter Outline 4.1 Earth and Sky 4.2 The Seasons 4.3 Keeping Time 4.4 The Calendar 4.5 Phases and Motions of the Moon 4.6 Ocean Tides and the Moon 4.7 Eclipses of the Sun and Moon Thinking Ahead If Earth’s orbit is nearly a perfect circle (as we saw in earlier chapters), why is it hotter in summer and colder in winter in many places around the globe? And why are the seasons in Australia or Peru the opposite of those in the United States or Europe? The story is told that Galileo, as he left the Hall of the Inquisition following his retraction of the doctrine that Earth rotates and revolves about the Sun, said under his breath, “But nevertheless it moves.” Historians are not sure whether the story is true, but certainly Galileo knew that Earth was in motion, whatever church authorities said. It is the motions of Earth that produce the seasons and give us our measures of time and date. The Moon’s motions around us provide the concept of the month and the cycle of lunar phases.
    [Show full text]
  • Sidereal Time Distribution in Large-Scale of Orbits by Usingastronomical Algorithm Method
    International Journal of Science and Research (IJSR) ISSN (Online): 2319-7064 Index Copernicus Value (2013): 6.14 | Impact Factor (2013): 4.438 Sidereal Time Distribution in Large-Scale of Orbits by usingAstronomical Algorithm Method Kutaiba Sabah Nimma 1UniversitiTenagaNasional,Electrical Engineering Department, Selangor, Malaysia Abstract: Sidereal Time literally means star time. The time we are used to using in our everyday lives is Solar Time.Astronomy, time based upon the rotation of the earth with respect to the distant stars, the sidereal day being the unit of measurement.Traditionally, the sidereal day is described as the time it takes for the Earth to complete one rotation relative to the stars, and help astronomers to keep them telescops directions on a given star in a night sky. In other words, earth’s rate of rotation determine according to fixed stars which is controlling the time scale of sidereal time. Many reserachers are concerned about how long the earth takes to spin based on fixed stars since the earth does not actually spin around 360 degrees in one solar day.Furthermore, the computations of the sidereal time needs to take a long time to calculate the number of the Julian centuries. This paper shows a new method of calculating the Sidereal Time, which is very important to determine the stars location at any given time. In addition, this method provdes high accuracy results with short time of calculation. Keywords: Sidereal time; Orbit allocation;Geostationary Orbit;SolarDays;Sidereal Day 1. Introduction (the upper meridian) in the sky[6]. Solar time is what the time we all use where a day is defined as 24 hours, which is The word "sidereal" comes from the Latin word sider, the average time that it takes for the sun to return to its meaning star.
    [Show full text]
  • Sidereal Time 1 Sidereal Time
    Sidereal time 1 Sidereal time Sidereal time (pronounced /saɪˈdɪəri.əl/) is a time-keeping system astronomers use to keep track of the direction to point their telescopes to view a given star in the night sky. Just as the Sun and Moon appear to rise in the east and set in the west, so do the stars. A sidereal day is approximately 23 hours, 56 minutes, 4.091 seconds (23.93447 hours or 0.99726957 SI days), corresponding to the time it takes for the Earth to complete one rotation relative to the vernal equinox. The vernal equinox itself precesses very slowly in a westward direction relative to the fixed stars, completing one revolution every 26,000 years approximately. As a consequence, the misnamed sidereal day, as "sidereal" is derived from the Latin sidus meaning "star", is some 0.008 seconds shorter than the earth's period of rotation relative to the fixed stars. The longer true sidereal period is called a stellar day by the International Earth Rotation and Reference Systems Service (IERS). It is also referred to as the sidereal period of rotation. The direction from the Earth to the Sun is constantly changing (because the Earth revolves around the Sun over the course of a year), but the directions from the Earth to the distant stars do not change nearly as much. Therefore the cycle of the apparent motion of the stars around the Earth has a period that is not quite the same as the 24-hour average length of the solar day. Maps of the stars in the night sky usually make use of declination and right ascension as coordinates.
    [Show full text]
  • Equation of Time — Problem in Astronomy M
    This paper was awarded in the II International Competition (1993/94) "First Step to Nobel Prize in Physics" and published in the competition proceedings (Acta Phys. Pol. A 88 Supplement, S-49 (1995)). The paper is reproduced here due to kind agreement of the Editorial Board of "Acta Physica Polonica A". EQUATION OF TIME | PROBLEM IN ASTRONOMY M. Muller¨ Gymnasium M¨unchenstein, Grellingerstrasse 5, 4142 M¨unchenstein, Switzerland Abstract The apparent solar motion is not uniform and the length of a solar day is not constant throughout a year. The difference between apparent solar time and mean (regular) solar time is called the equation of time. Two well-known features of our solar system lie at the basis of the periodic irregularities in the solar motion. The angular velocity of the earth relative to the sun varies periodically in the course of a year. The plane of the orbit of the earth is inclined with respect to the equatorial plane. Therefore, the angular velocity of the relative motion has to be projected from the ecliptic onto the equatorial plane before incorporating it into the measurement of time. The math- ematical expression of the projection factor for ecliptic angular velocities yields an oscillating function with two periods per year. The difference between the extreme values of the equation of time is about half an hour. The response of the equation of time to a variation of its key parameters is analyzed. In order to visualize factors contributing to the equation of time a model has been constructed which accounts for the elliptical orbit of the earth, the periodically changing angular velocity, and the inclined axis of the earth.
    [Show full text]
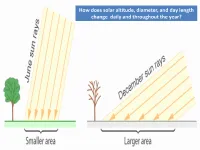
  • How Does Solar Altitude, Diameter, and Day Length Change Daily and Throughout the Year?
    How does solar altitude, diameter, and day length change daily and throughout the year? Let’s prove distance doesn’t matter in seasons by investigating SOLAR ALTITUDE, DAY LENGTH and SOLAR DISTANCE… Would the sun have the same appearance if you observed it from other planets? Why do we see the sun at different altitudes throughout the day? We use the altitude of the sun at a time called solar “noon” because of daily solar altitude changes from the horizon at sunrise and sunset to it’s maximum daily altitude at noon. If you think solar noon is at 12:00:00, you’re mistaken! Solar “noon” doesn’t usually happen at clock-noon at your longitude for lots of reasons! SOLAR INTENSITY and ALTITUDE - Maybe a FLASHLIGHT will help us see this relationship! Draw the beam shape for 3 solar altitudes in your notebooks! How would knowing solar altitude daily and seasonally help make solar panels (collectors)work best? Where would the sun have to be located to capture the maximum amount of sunlight energy? Draw the sun in the right position to maximize the light it receives on panel For the northern hemisphere, in which general direction would they be pointed? For the southern hemisphere, in which direction would they be pointed? SOLAR PANELS at different ANGLES ON GROUND How do shadows show us solar altitude? You used a FLASHLIGHT and MODELING CLAY to show you how SOLAR INTENSITY, ALTITUDE, and SHADOW LENGTH are related! Using at least three solar altitudes and locations, draw your conceptual model of this relationship in your notebooks… Label: Sun compass direction Shadow compass direction Solar altitude Shadow length (long/short) Sun intensity What did the lab show us about how SOLAR ALTITUDE, DIAMETER, & DAY LENGTH relate to each other? YOUR GRAPHS are PROBABLY the easiest way to SEE the RELATIONSHIPS.
    [Show full text]
  • Lecture 6: Where Is the Sun?
    4.430 Daylighting Massachusetts Institute of Technology Christoph Reinhart Department of Architecture 4.430 Where is the sun? Building Technology Program Goals for This Week Where is the sun? Designing Static Shading Systems MIT 4.430 Daylighting, Instructor C Reinhart 1 1 MISC Meeting on group projects Reduce HDR image size via pfilt –x 800 –y 550 filne_name_large.pic > filename_small>.pic Note: pfilt is a Radiance program. You can find further info on pfilt by googeling: “pfilt Radiance” MIT 4.430 Daylighting, Instructor C Reinhart 2 2 Daylight Factor Hand Calculation Mean Daylight Factor according to Lynes Reinhart & LoVerso, Lighting Research & Technology (2010) Move into the building, design the facade openings, room dimensions and depth of the daylit area. Determine the required glazing area using the Lynes formula. A glazing = required glazing area A total = overall interior surface area (not floor area!) R mean = area-weighted mean surface reflectance vis = visual transmittance of glazing units = sun angle 3 ‘Validation’ of Daylight Factor Formula Reinhart & LoVerso, Lighting Research & Technology (2010) Graph of mean daylighting factor according to Lynes formula v. Radiance removed due to copyright restrictions. Source: Figure 5 in Reinhart, C. F., and V. R. M. LoVerso. "A Rules of Thumb Based Design Sequence for Diffuse Daylight." Lighting Research and Technology 42, no. 1 (2010): 7-32. Comparison to Radiance simulations for 2304 spaces. Quality control for simulations. LEED 2.2 Glazing Factor Formula Graph of mean daylighting factor according to LEED 2.2 v. Radiance removed due to copyright restrictions. Source: Figure 11 in Reinhart, C. F., and V.
    [Show full text]
  • The Solar Resource
    CHAPTER 7 THE SOLAR RESOURCE To design and analyze solar systems, we need to know how much sunlight is available. A fairly straightforward, though complicated-looking, set of equations can be used to predict where the sun is in the sky at any time of day for any location on earth, as well as the solar intensity (or insolation: incident solar Radiation) on a clear day. To determine average daily insolation under the com- bination of clear and cloudy conditions that exist at any site we need to start with long-term measurements of sunlight hitting a horizontal surface. Another set of equations can then be used to estimate the insolation on collector surfaces that are not flat on the ground. 7.1 THE SOLAR SPECTRUM The source of insolation is, of course, the sun—that gigantic, 1.4 million kilo- meter diameter, thermonuclear furnace fusing hydrogen atoms into helium. The resulting loss of mass is converted into about 3.8 × 1020 MW of electromagnetic energy that radiates outward from the surface into space. Every object emits radiant energy in an amount that is a function of its tem- perature. The usual way to describe how much radiation an object emits is to compare it to a theoretical abstraction called a blackbody. A blackbody is defined to be a perfect emitter as well as a perfect absorber. As a perfect emitter, it radiates more energy per unit of surface area than any real object at the same temperature. As a perfect absorber, it absorbs all radiation that impinges upon it; that is, none Renewable and Efficient Electric Power Systems.
    [Show full text]
  • Solar Time, Legal Time, Time in Use
    Home Search Collections Journals About Contact us My IOPscience Solar time, legal time, time in use This article has been downloaded from IOPscience. Please scroll down to see the full text article. 2011 Metrologia 48 S181 (http://iopscience.iop.org/0026-1394/48/4/S08) View the table of contents for this issue, or go to the journal homepage for more Download details: IP Address: 193.2.92.136 The article was downloaded on 30/09/2011 at 13:28 Please note that terms and conditions apply. IOP PUBLISHING METROLOGIA Metrologia 48 (2011) S181–S185 doi:10.1088/0026-1394/48/4/S08 Solar time, legal time, time in use Bernard Guinot Observatoire de Paris, 61 avenue de l’Observatoire, F-75014 Paris, France Received 21 February 2011, in final form 22 March 2011 Published 20 July 2011 Online at stacks.iop.org/Met/48/S181 Abstract The International Conference held in 1884 at Washington defined a universal time as the mean solar time at the Greenwich meridian (GMT). Now, the Universal Time, version UT1, is strictly defined as proportional to the angle of rotation of the Earth in space. In this evolution, the departure of UT1 from GMT does not exceed one or two seconds. This is quite negligible when compared with the departure between the solar time and the legal time of citizens, which may exceed two hours without raising protests. 1. Introduction However, sterile discussions motivated by national pride delayed the conclusions of the conference by one month. These The time that governs biological processes at the surface of the conclusions were finally in conformity with those of the Rome Earth follows the apparent motion of the Sun at the location conference.
    [Show full text]
  • What Causes the Seasons? These Images of the Sun Were Taken 6 Months Apart
    2/11/09 We can recognize solstices and equinoxes by If you are located in the continental U.S. on the first Sun’s path across sky: day of October, how will the position of the Sun at noon be different two weeks later? Summer solstice: Highest path, rise and set at most A. It will have moved toward the north. extreme north of due east. B. It will have moved to a position higher in the sky. C. It will stay in the same position. Winter solstice: Lowest D. It will have moved to a position closer to the path, rise and set at most extreme south of due horizon. east. E. It will have moved toward the west. Equinoxes: Sun rises precisely due east and sets precisely due west. NORTH For an observer in the Shadow Under which of the following circumstances will plot A continental U.S., which of Shadow plot B a vertical flagpole not cast a shadow as seen WEST from the continental United States? the three shadow plots, EAST shown at right, correctly Shadow plot C depicts the Sun’s motion for SOUTH A. every day at noon one day? B. every day at the time when the sun is highest in the sky C. when the sun is highest in the sky on the summer A. Shadow plot A solstice B. Shadow plot B C. Shadow plot C D. when the sun is highest in the sky on the winter solstice D. More than one of the plots are possible, on different days of E.
    [Show full text]
  • Sunearthtools.Com Tools for Consumers and Designers of Solar Home Tools Solar Sun Position Photovoltaic Payback Photovoltaic FAQ Sunrise Sunset Calendar
    Sun position chart, solar path diagram, solar angle declination zenith, hour sunrise sunset ... Page 1 of 6 SunEarthTools.com Tools for consumers and designers of solar Home Tools Solar Sun Position Photovoltaic payback Photovoltaic FAQ SunRise SunSet Calendar Home > Solar > Sun Position 19:41 | Thursday 14 February 2013 select your points search 34.393751, -118.585747 34° 23' 37.504" N 118° 35' 8.689" W SunRise: 06:40:11 * 105.02° | SunSet: 17:37:16 * 255.17° | 26039 Sandburg Place, Stevenson Ranch, CA 91381, USA Home Name execute Solar Disk Analemma Solstice Photovoltaic payback year month day hour minute See Todays Mortgage Rates Sun Position www.MortgageRates.LowerMyBills.com 2013 02 14 10 41 Time CO2 Emissions Rates Hit New Lows at 2.5%(2.9%APR) FHA Cuts Mortgage Requirement! GMT-8 DST Default zone Unit of measure converter Mode: sun path Full interactive map Interactive Map Distance Coordinates conversion SunRise SunSet Calendar Photovoltaic FAQ Insert this map tool in your site This work is licenced under a Creative Commons Licence Back to top Content | Data + Map | Chart Polar | Chart Cartesian | Table | You can copy some of the articles linking always the source. Visits: on Line: p:1 http://www.sunearthtools.com/dp/tools/pos_sun.php 2/14/2013 Sun position chart, solar path diagram, solar angle declination zenith, hour sunrise sunset ... Page 2 of 6 Back to top Content | Data + Map | Chart Polar | Chart Cartesian | Table | Back to top Content | Data + Map | Chart Polar | Chart Cartesian | Table | sun position Elevation Azimuth latitude longitude 34.393751° 118.585747° 14/02/2013 10:41 38.46° 152.35° N W Azimuth Azimuth Sunrise Sunset twilight Sunrise Sunset twilight -0.833° 06:40:11 17:37:16 105.02° 255.17° Civil twilight -6° 06:14:27 18:02:58 101.46° 258.74° http://www.sunearthtools.com/dp/tools/pos_sun.php 2/14/2013 Sun position chart, solar path diagram, solar angle declination zenith, hour sunrise sunset ..
    [Show full text]