Efficiently Computing Vortex Lattices in Rapid Rotating Bose–Einstein
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

International Naming Conventions NAFSA TX State Mtg
1 2 3 4 1. Transcription is a more phonetic interpretation, while transliteration represents the letters exactly 2. Why transcription instead of transliteration? • Some English vowel sounds don’t exist in the other language and vice‐versa • Some English consonant sounds don’t exist in the other language and vice‐versa • Some languages are not written with letters 3. What issues are related to transcription and transliteration? • Lack of consistent rules from some languages or varying sets of rules • Country variation in choice of rules • Country/regional variations in pronunciation • Same name may be transcribed differently even within the same family • More confusing when common or religious names cross over several countries with different scripts (i.e., Mohammad et al) 5 Dark green countries represent those countries where Arabic is the official language. Lighter green represents those countries in which Arabic is either one of several official languages or is a language of everyday usage. Middle East and Central Asia: • Kurdish and Turkmen in Iraq • Farsi (Persian) and Baluchi in Iran • Dari, Pashto and Uzbek in Afghanistan • Uyghur, Kazakh and Kyrgyz in northwest China South Asia: • Urdu, Punjabi, Sindhi, Kashmiri, and Baluchi in Pakistan • Urdu and Kashmiri in India Southeast Asia: • Malay in Burma • Used for religious purposes in Malaysia, Indonesia, southern Thailand, Singapore, and the Philippines Africa: • Bedawi or Beja in Sudan • Hausa in Nigeria • Tamazight and other Berber languages 6 The name Mohamed is an excellent example. The name is literally written as M‐H‐M‐D. However, vowels and pronunciation depend on the region. D and T are interchangeable depending on the region, and the middle “M” is sometimes repeated when transcribed. -

Is Shuma the Chinese Analog of Soma/Haoma? a Study of Early Contacts Between Indo-Iranians and Chinese
SINO-PLATONIC PAPERS Number 216 October, 2011 Is Shuma the Chinese Analog of Soma/Haoma? A Study of Early Contacts between Indo-Iranians and Chinese by ZHANG He Victor H. Mair, Editor Sino-Platonic Papers Department of East Asian Languages and Civilizations University of Pennsylvania Philadelphia, PA 19104-6305 USA [email protected] www.sino-platonic.org SINO-PLATONIC PAPERS FOUNDED 1986 Editor-in-Chief VICTOR H. MAIR Associate Editors PAULA ROBERTS MARK SWOFFORD ISSN 2157-9679 (print) 2157-9687 (online) SINO-PLATONIC PAPERS is an occasional series dedicated to making available to specialists and the interested public the results of research that, because of its unconventional or controversial nature, might otherwise go unpublished. The editor-in-chief actively encourages younger, not yet well established, scholars and independent authors to submit manuscripts for consideration. Contributions in any of the major scholarly languages of the world, including romanized modern standard Mandarin (MSM) and Japanese, are acceptable. In special circumstances, papers written in one of the Sinitic topolects (fangyan) may be considered for publication. Although the chief focus of Sino-Platonic Papers is on the intercultural relations of China with other peoples, challenging and creative studies on a wide variety of philological subjects will be entertained. This series is not the place for safe, sober, and stodgy presentations. Sino- Platonic Papers prefers lively work that, while taking reasonable risks to advance the field, capitalizes on brilliant new insights into the development of civilization. Submissions are regularly sent out to be refereed, and extensive editorial suggestions for revision may be offered. Sino-Platonic Papers emphasizes substance over form. -

Cha Zhang, Chang−Shui Zhang, Chengcui Zhang, Dengsheng Zhang, Dong Zhang, Dongming Zhang, Hong−Jiang Zhang, Jiang Zhang, Jianning Zhang, Keqi Zhang, Lei Zhang, Li
Z Zeng, Wenjun Zeng, Zhihong Zhai, Yun Zhang, Benyu Zhang, Cha Zhang, Chang−Shui Zhang, Chengcui Zhang, Dengsheng Zhang, Dong Zhang, Dongming Zhang, Hong−Jiang Zhang, Jiang Zhang, Jianning Zhang, Keqi Zhang, Lei Zhang, Li Menu Next Z Zhang, Like Zhang, Meng Zhang, Mingju Zhang, Rong Zhang, Ruofei Zhang, Weigang Zhang, Yongdong Zhang, Yun−Gang Zhang, Zhengyou Zhang, Zhenping Zhang, Zhenqiu Zhang, Zhishou Zhang, Zhongfei (Mark) Zhao, Frank Zhao, Li Zhao, Na Prev Menu Next Z Zheng, Changxi Zheng, Yizhan Zhi, Yang Zhong, Yuzhuo Zhou, Jin Zhu, Jiajun Zhu, Xiaoqing Zhu, Yongwei Zhuang, Yueting Zimmerman, John Zoric, Goranka Zou, Dekun Prev Menu Wenjun Zeng Organization : University of Missouri−Columbia, United States of America Paper(s) : ON THE RATE−DISTORTION PERFORMANCE OF DYNAMIC BITSTREAM SWITCHING MECHANISMS (Abstract) Letter−Z Menu Zhihong Zeng Organization : University of Illinois at Urbana−Champaign, United States of America Paper(s) : AUDIO−VISUAL AFFECT RECOGNITION IN ACTIVATION−EVALUATION SPACE (Abstract) Letter−Z Menu Yun Zhai Organization : University of Central Florida, United States of America Paper(s) : AUTOMATIC SEGMENTATION OF HOME VIDEOS (Abstract) Letter−Z Menu Benyu Zhang Organization : Microsoft Research Asia, China Paper(s) : SUPERVISED SEMI−DEFINITE EMBEDING FOR IMAGE MANIFOLDS (Abstract) Letter−Z Menu Cha Zhang Organization : Microsoft Research, United States of America Paper(s) : HYBRID SPEAKER TRACKING IN AN AUTOMATED LECTURE ROOM (Abstract) Letter−Z Menu Chang−Shui Zhang Organization : Tsinghua University, China -

中国人的姓名 王海敏 Wang Hai Min
中国人的姓名 王海敏 Wang Hai min last name first name Haimin Wang 王海敏 Chinese People’s Names Two parts Last name First name 姚明 Yao Ming Last First name name Jackie Chan 成龙 cheng long Last First name name Bruce Lee 李小龙 li xiao long Last First name name The surname has roughly several origins as follows: 1. the creatures worshipped in remote antiquity . 龙long, 马ma, 牛niu, 羊yang, 2. ancient states’ names 赵zhao, 宋song, 秦qin, 吴wu, 周zhou 韩han,郑zheng, 陈chen 3. an ancient official titles 司马sima, 司徒situ 4. the profession. 陶tao,钱qian, 张zhang 5. the location and scene in residential places 江jiang,柳 liu 6.the rank or title of nobility 王wang,李li • Most are one-character surnames, but some are compound surname made up of two of more characters. • 3500Chinese surnames • 100 commonly used surnames • The three most common are 张zhang, 王wang and 李li What does my name mean? first name strong beautiful lively courageous pure gentle intelligent 1.A person has an infant name and an official one. 2.In the past,the given names were arranged in the order of the seniority in the family hierarchy. 3.It’s the Chinese people’s wish to give their children a name which sounds good and meaningful. Project:Search on-Line www.Mandarinintools.com/chinesename.html Find Chinese Names for yourself, your brother, sisters, mom and dad, or even your grandparents. Find meanings of these names. ----What is your name? 你叫什么名字? ni jiao shen me ming zi? ------ 我叫王海敏 wo jiao Wang Hai min ------ What is your last name? 你姓什么? ni xing shen me? (你贵姓?)ni gui xing? ------ 我姓 王,王海敏。 wo xing wang, Wang Hai min ----- What is your nationality? 你是哪国人? ni shi na guo ren? ----- I am chinese/American 我是中国人/美国人 Wo shi zhong guo ren/mei guo ren 百家 姓 bai jia xing 赵(zhào) 钱(qián) 孙(sūn) 李(lǐ) 周(zhōu) 吴(wú) 郑(zhèng) 王(wán 冯(féng) 陈(chén) 褚(chǔ) 卫(wèi) 蒋(jiǎng) 沈(shěn) 韩(hán) 杨(yáng) 朱(zhū) 秦(qín) 尤(yóu) 许(xǔ) 何(hé) 吕(lǚ) 施(shī) 张(zhāng). -

Lǎoshī Hé Xuéshēng (Teacher and Students)
© Copyright, Princeton University Press. No part of this book may be distributed, posted, or reproduced in any form by digital or mechanical means without prior written permission of the publisher. CHAPTER Lǎoshī hé Xuéshēng 1 (Teacher and Students) Pinyin Text English Translation (A—Dīng Yī, B—Wáng Èr, C—Zhāng Sān) (A—Ding Yi, B—Wang Er, C—Zhang San) A: Nínhǎo, nín guìxìng? A: Hello, what is your honorable surname? B: Wǒ xìng Wáng, jiào Wáng Èr. Wǒ shì B: My surname is Wang. I am called Wang Er. lǎoshī. Nǐ xìng shénme? I am a teacher. What is your last name? A: Wǒ xìng Dīng, wǒde míngzi jiào Dīng Yī. A: My last name is Ding and my full name is Wǒ shì xuéshēng. Ding Yi. I am a student. 老师 老師 lǎoshī n. teacher 和 hé conj. and 学生 學生 xuéshēng n. student 您 nín pron. honorific form of singular you 好 hǎo adj. good 你(您)好 nǐ(nín)hǎo greeting hello 贵 貴 guì adj. honorable 贵姓 貴姓 guìxìng n./v. honorable surname (is) 我 wǒ pron. I; me 姓 xìng n./v. last name; have the last name of … 王 Wáng n. last name Wang 叫 jiào v. to be called 二 èr num. two (used when counting; here used as a name) 是 shì v. to be (any form of “to be”) 10 © Copyright, Princeton University Press. No part of this book may be distributed, posted, or reproduced in any form by digital or mechanical means without prior written permission of the publisher. -

Ideophones in Middle Chinese
KU LEUVEN FACULTY OF ARTS BLIJDE INKOMSTSTRAAT 21 BOX 3301 3000 LEUVEN, BELGIË ! Ideophones in Middle Chinese: A Typological Study of a Tang Dynasty Poetic Corpus Thomas'Van'Hoey' ' Presented(in(fulfilment(of(the(requirements(for(the(degree(of(( Master(of(Arts(in(Linguistics( ( Supervisor:(prof.(dr.(Jean=Christophe(Verstraete((promotor)( ( ( Academic(year(2014=2015 149(431(characters Abstract (English) Ideophones in Middle Chinese: A Typological Study of a Tang Dynasty Poetic Corpus Thomas Van Hoey This M.A. thesis investigates ideophones in Tang dynasty (618-907 AD) Middle Chinese (Sinitic, Sino- Tibetan) from a typological perspective. Ideophones are defined as a set of words that are phonologically and morphologically marked and depict some form of sensory image (Dingemanse 2011b). Middle Chinese has a large body of ideophones, whose domains range from the depiction of sound, movement, visual and other external senses to the depiction of internal senses (cf. Dingemanse 2012a). There is some work on modern variants of Sinitic languages (cf. Mok 2001; Bodomo 2006; de Sousa 2008; de Sousa 2011; Meng 2012; Wu 2014), but so far, there is no encompassing study of ideophones of a stage in the historical development of Sinitic languages. The purpose of this study is to develop a descriptive model for ideophones in Middle Chinese, which is compatible with what we know about them cross-linguistically. The main research question of this study is “what are the phonological, morphological, semantic and syntactic features of ideophones in Middle Chinese?” This question is studied in terms of three parameters, viz. the parameters of form, of meaning and of use. -
![Arxiv:2104.04497V1 [Cs.CL] 9 Apr 2021](https://docslib.b-cdn.net/cover/6530/arxiv-2104-04497v1-cs-cl-9-apr-2021-1186530.webp)
Arxiv:2104.04497V1 [Cs.CL] 9 Apr 2021
Chinese Character Decomposition for Neural MT with Multi-Word Expressions Lifeng Han1, Gareth J. F. Jones1, Alan F. Smeaton2 and Paolo Bolzoni 1 ADAPT Research Centre 2 Insight Centre for Data Analytics School of Computing, Dublin City University, Dublin, Ireland [email protected], [email protected] Abstract porating sub-word knowledge using Byte Pair En- coding (BPE) (Sennrich et al., 2016). However, Chinese character decomposition has been such methods cannot be directly applied to Chi- used as a feature to enhance Machine nese, Japanese and other ideographic languages. Translation (MT) models, combining rad- Integrating sub-character level information, icals into character and word level mod- such as Chinese ideograph and radicals as learning els. Recent work has investigated ideo- knowledge has been used to enhance features in graph or stroke level embedding. How- NMT systems (Han and Kuang, 2018; Zhang and ever, questions remain about different de- Matsumoto, 2018; Zhang and Komachi, 2018). composition levels of Chinese character Han and Kuang (2018), for example, explain that representations, radical and strokes, best the meaning of some unseen or low frequency Chi- suited for MT. To investigate the impact nese characters can be estimated and translated us- of Chinese decomposition embedding in ing radicals decomposed from the Chinese char- detail, i.e., radical, stroke, and intermedi- acters, as long as the learning model can acquire ate levels, and how well these decomposi- knowledge of these radicals within the training tions represent the meaning of the original corpus. character sequences, we carry out analy- Chinese characters often include two pieces of sis with both automated and human evalu- information, with semantics encoded within radi- ation of MT. -

Yubin Zeng Resume 1
CURRICULUM VITAE Yubin Zeng Department of Water Quality Engineering, Wuhan University No.8 East Lake Road South, Wuchang District, 430072, Wuhan, China PERSONAL Position: Associate professor, vice director of Water Quality Engineering E-mail: [email protected]; [email protected] Personal webpage: http://pmc.whu.edu.cn/teachers/185.html EDUCATION B. Eng. – Department of Chemical Engineering, East China University of Science and Technology, China (1991). M. Sc. – Department of Applied Chemistry, Huazhong University of Science and Technology, China (2000). Ph. D. – Department of Environmental Science and Engineering, Huazhong University of Science and Technology, China (2007). Post-doctor fellowship – Department of Civil and Environmental Engineering, Seoul National University, Korea (2009). TEACHING 1. Separation Processes of Chemical Engineering (to graduate students) 2. Theory and Technology of Water Treatment (to undergraduate students) 3. Water Treatment Experiment (to undergraduate students) 4. Wastewater Reuse Technology (to undergraduate students) RESEARCH 1 Research interests 1. Water and wastewater treatment for reuse. 2. Environmental nanomaterials and technology. 3. Remediation of ground and underground water. Research in progress 1. Funds supported from industry. “Treatment and reuse of high salt wastewater with high temperature from oil field”, Project Leader. 2. Funds supported from industry. “Biologic treatment and discharge of wastewater from heavy oil’ process and production”, Project Leader. 3. Open Funds for State Key Lab of Biogeology and Environmental Geology, China (GBL21311): “Study on remediation of chlorinated hydrocarbons by nano composite materials/microorganism”, Project Leader. 4. National planning project on innovation and entrepreneurship training of China University (201410486051): “Research on mechanism and application on organic molecule modification of nano core-shell magnetic composite”, Project Leader. -

WEI ZHENG, Ph.D., ATS
Dr. Zheng: 1 of 38 CURRICULUM VITAE WEI ZHENG, Ph.D., ATS BUSINESS ADDRESS School of Health Sciences College of Health and Human Sciences Purdue University 550 Stadium Mall Drive, HAMP-1169 West Lafayette, IN 47907 Phone: (765) 496-6447; Fax: (765) 496-1377; Email: [email protected] PERSONAL DATA Citizenship: American Citizen Marital Status: Married with two children PART I: TRANING AND PROFESSIONAL EXPERIENCE PROFESSIONAL TRAINING 1977-1981 Bachelor of Science in Pharmacy College of Pharmacy, Zhejiang University, Hangzhou, PRC 1981-1984 Master of Science in Pharmacology Department of Pharmacology, Zhejiang University College of Pharmacy 1986-1991 Doctor of Philosophy in Pharmacology and Toxicology Department of Pharmacology and Toxicology, University of Arizona College of Pharmacy, Tucson, Arizona 1991-1992 Postdoctoral/Research Fellow Mentor: Dr. I. Glenn Sipes, Head, Department of Pharmacology, School of Medicine, University of Arizona. President of the Society of Toxicology (1991-1992) 2009 Feb Leadership Training Camp CIC (Committee on Institutional Cooperation) Dept. Chairs/Heads Forum, Chicago. ACADEMIC AND PROFESSIONAL APPOINTMENT 1975-1977 Research Technician (Analyst Assistant) Experimental Pharmaceutical Factory of Zhejiang University, Hangzhou, PRC 1984-1986 Lecturer of Pharmacology Department of Pharmacology, Zhejiang University College of Pharmacy, Hangzhou, PRC 1986-1991 Graduate Research Assistant Department of Pharmacology and Toxicology, University of Arizona, Tucson, AZ 1992-1993 University of Arizona, Tucson, Arizona Research Assistant Scientist (non-tenure faculty position). Dept. of Pharmacology and Toxicology, College of Pharmacy, University of Arizona, Tucson, AZ. 1993-2003 Columbia University, New York, New York • Assistant Professor of Public Health and Pharmacology (1993-1999) and • Associate Professor (tenured, 2000-2003), a joint faculty position in Dept. -

Huawei Zeng, Ph.D. Research Interests: Obesity Related Colon
Huawei Zeng, Ph.D. Research Interests: Obesity related colon cancer is a significant global health concern and the impact of specific dietary components on colon cancer risk has been well recognized. Dr. Zeng's main area of research is to determine the molecular mechanisms of cancer-preventive nutrients in foods. This focus presently centers on dietary fiber / diet timing and gut microbiome, and the development of new molecular biomarkers for obesity related colon cancer prevention. Currently, Dr. Zeng is studying the effects of secondary bile acids and short chain fatty acids in the colon: a focus on colonic microbiome, cell proliferation, inflammation, and cancer. Dr. Zeng is also investigating the impact of human genetic variation on optimal nutritional intake. Single nucleotide polymorphisms (SNPs) are a primary component of human genetic variation. To determine the diet that best fits certain SNPs, He examines the effects of hemochromatosis, selenoproteins and vitamin D receptor genotypes on the absorption and utilization of iron, selenium, calcium and other nutrients. Education: B.Sc.,Biology, Xiamen University, Xiamen, China, 1984 M.Sc., Biology, Xiamen University, Xiamen, China, 1987 Ph.D., Molecular Biology, University of Wyoming, Laramie, WY, USA, 1996 Professional Experience: 1987-1989 Researcher, Xiamen Fishery Research Institute, Xiamen, China 1989-1991 Visiting Scholar, Dept. Biological Sci., SUNY-Buffalo, Buffalo, NY. 1991-1996 Research Assistant, Dept. Molecular Biology, Univ. Wyoming, Laramie, WY. 1996-1999 Intramural Research Training Fellow, Laboratory of Molecular & Cellular Biology, NIDDK, NIH, Bethesda, MD. 1999-present Research Molecular Biologist, USDA ARS Grand Forks Human Nutrition Research Center, Grand Forks, ND. 2000-present Adjunct Professor, Dept. -
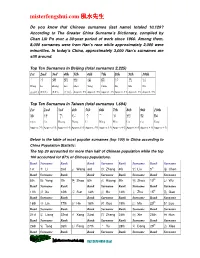
Misterfengshui.Com 風水先生
misterfengshui.com 風水先生 Do you know that Chinese surnames (last name) totaled 10,129? According to The Greater China Surname’s Dictionary, compiled by Chan Lik Pu over a 30-year period of work since 1960. Among them, 8,000 surnames were from Han’s race while approximately 2,000 were minorities. In today’s China, approximately 3,000 Han’s surnames are still around. Top Ten Surnames In Beijing (total surnames 2,225) 1st 2nd 3rd 4th 5th 6th 7th 8th 9th 10th 王 李 張 劉 趙 楊 陳 徐 馬 吳 Wang Li Zhang Liu Zhao Yang Chen Xu Ma Wu (10.6% ) (9.6%) (9.6%) (7.7% ) Approx. 5% Approx. 5% Approx. 4% Approx. 4% Approx. 4% Approx. 3% Top Ten Surnames In Taiwan (total surnames 1,694) 1st 2nd 3rd 4th 5th 6th 7th 8th 9th 10th 陳 林 黃 張 李 王 吳 劉 蔡 楊 Chen Lin Huang Zhang Li Wang Wux. Liu Cai Yang Approx .7% Approx 6 % Approx 6 % Approx 6 % Approx. 5% Approx 5 % Approx 4 % Approx 4 % Approx 4 % Approx 4 % Below is the table of most popular surnames (top 100) in China according to China Population Statistic: The top 20 accounted for more than half of Chinese population while the top 100 accounted for 87% of Chinese populations. Rank Surname Rank Rank Surname Rank Surname Rank Surname 1st 李 Li 2nd 王 Wang 3rd 張 Zhang 4th 劉 Liu 5th 陳 Chen Rank Surname Rank Rank Surname Rank Surname Rank Surname 6th 楊 Yang 7th 趙 Zhao 8th 黃 Huang 9th 周 Zhou 10 th 吳 Wu Rank Surname Rank Rank Surname Rank Surname Rank Surname 11th 徐 Xu 12th 孫 Sun 13th 胡 Hu 14th 朱 Zhu 15 th 高 Gao Rank Surname Rank Rank Surname Rank Surname Rank Surname 16th 林 Lin 17th 何 He 18th 郭 Guo 19th 馬 Ma 20 th 羅 Luo Rank -

Representing Talented Women in Eighteenth-Century Chinese Painting: Thirteen Female Disciples Seeking Instruction at the Lake Pavilion
REPRESENTING TALENTED WOMEN IN EIGHTEENTH-CENTURY CHINESE PAINTING: THIRTEEN FEMALE DISCIPLES SEEKING INSTRUCTION AT THE LAKE PAVILION By Copyright 2016 Janet C. Chen Submitted to the graduate degree program in Art History and the Graduate Faculty of the University of Kansas in partial fulfillment of the requirements for the degree of Doctor of Philosophy. ________________________________ Chairperson Marsha Haufler ________________________________ Amy McNair ________________________________ Sherry Fowler ________________________________ Jungsil Jenny Lee ________________________________ Keith McMahon Date Defended: May 13, 2016 The Dissertation Committee for Janet C. Chen certifies that this is the approved version of the following dissertation: REPRESENTING TALENTED WOMEN IN EIGHTEENTH-CENTURY CHINESE PAINTING: THIRTEEN FEMALE DISCIPLES SEEKING INSTRUCTION AT THE LAKE PAVILION ________________________________ Chairperson Marsha Haufler Date approved: May 13, 2016 ii Abstract As the first comprehensive art-historical study of the Qing poet Yuan Mei (1716–97) and the female intellectuals in his circle, this dissertation examines the depictions of these women in an eighteenth-century handscroll, Thirteen Female Disciples Seeking Instructions at the Lake Pavilion, related paintings, and the accompanying inscriptions. Created when an increasing number of women turned to the scholarly arts, in particular painting and poetry, these paintings documented the more receptive attitude of literati toward talented women and their support in the social and artistic lives of female intellectuals. These pictures show the women cultivating themselves through literati activities and poetic meditation in nature or gardens, common tropes in portraits of male scholars. The predominantly male patrons, painters, and colophon authors all took part in the formation of the women’s public identities as poets and artists; the first two determined the visual representations, and the third, through writings, confirmed and elaborated on the designated identities.