On a Theorem of Pelc and Prikry on the Nonexistence of Invariant
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
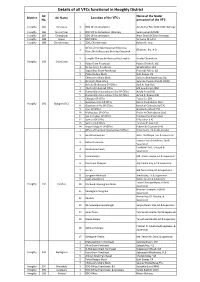
Details of All Vfcs Functional in Hooghly District AC Name of the Nodal District AC Name Location of the Vfcs No
Details of all VFCs functional in Hooghly District AC Name of the Nodal District AC Name Location of the VFCs No. personnel of the VFC Hooghly 185 Uttarpara 1 SDO Office,serampore Asit Kumar Paul (UDC),Roll-Incharge Hooghly 186 Sreerampur 1 BDO Office,Serampore-Uttarpara Samir sarkar (EOME) Hooghly 187 Champdani 1 SDO Office,serampore Amal Dey (UDC),Roll-Incharge Hooghly 188 Singur 1 BDO Office Sumanta Ghoshal Hooghly 189 Chandannagar 1 SDO, Chandannagar Kalyan Kr. Jana Office of the Sub Divisional Officer,1st 1 Bikash Kr. Jha, A.O. Floor,Old Collectorate Building,Chinsurah 2 Hooghly Chinsurah Municipality,Hooghly Sandip Chowdhury, Hooghly 190 Chunchura 3 Polba Gram Panchayat Palash Ch Malik, VLE 4 Rajhat Gram Panchayat Sk Sahajahan, VLE 5 Sugandhya Gram Panchayat Prasenjit Pakira, VLE 6 Polba-Dadpur Block Udit Biswas, PA 7 Chinsurah-Mogra Block Santanu Bandopadhyay,Opt 1 Balagarh Block office Subrata Chandra Pandit (OCM) 2 Bakulia Dhobapara GP Office Sujit Kr Nag (Sec) 3 Charkrishnabati GP Office Md Azizul Islam (NS) 4 Dumurdaha Nityandapur 1 No GP Office Arnab Panja (NS) 5 Dumurdaha Nityandapur 2 No GP Office Ashok Kr Biswas (EA) 6 Ektarpur GP Office Tapas Das (EA) 7 Guptipara I No GP Office Kanak Chakroborty (Sec) Hooghly 191 Balagarh (SC) 8 Guptipara II No GP Office Kanchan Chakroborty (EA) 9 Jirat GP Office Gopikanta Ghosh (EA) 10 Mohipalpur GP Office Prabir Kr Chakroborty (Sec) 11 Sija Kamalpur GP Office Dinabandhu Ghosh (Sec) 12 Somra I GP Office Dilip Lohar (EA) 13 Somra II GP Office Tanmoy Kr Sow (EA) 14 Sripur Balagarh GP Office Dibyendu Goswami (EA) 1 Office of the Block Development Officer Priya Gupta, PA & AO, Pandua 2 Bantika-Boinchee Ashis Chatterjee, Sec & Supervisor Jayanta Roy Chowdhury, Opt& 3 Belun-Dhamasin Supervisor SHANKAR DAS, Sahayak & 4 Berela-konchmali Supervisor 5 Haral-Daspur Md. -

Duare Sarkar & Paray Samadhan,2021
DUARE SARKAR & PARAY SAMADHAN,2021 CAMP SCHEDULE OF DISTRICT HOOGHLY Camp Sl No District BLock/Local Body GP/Ward Venue Date 1 16-08-2021 HOOGHLY Tarakeswar (M) Ward - 008,Ward - 009,Ward - SAHAPUR PRY. SCHOOL 2 16-08-2021 HOOGHLY Champdany (M) Ward - 005 UPHC II HEALTH CENTER 3 16-08-2021 HOOGHLY Chandannagar MC (M) Ward - 003 Goswami Ghat Community Hall Ward - 018,Ward - 019,Ward - NAGENDRANATH KUNDU 4 16-08-2021 HOOGHLY Konnagar (M) 020 VIDYAMANDIR CHAMPDANY BISS FREE PRIMARY 5 16-08-2021 HOOGHLY Champdany (M) Ward - 002 SCHOOL 6 16-08-2021 HOOGHLY SINGUR SINGUR-II Gopalnagar K.R. Dey High School 7 16-08-2021 HOOGHLY GOGHAT-1 BALI BALI HIGH SCHOOL 8 16-08-2021 HOOGHLY BALAGARH MOHIPALPUR Mohipalpur Primary School 9 16-08-2021 HOOGHLY MOGRA-CHUNCHURA MOGRA-I Mogra Uttam Chandra High School 10 16-08-2021 HOOGHLY BALAGARH EKTARPUR Ekterpur U HS 11 16-08-2021 HOOGHLY TARAKESWAR SANTOSHPUR Gouribati Radharani Das High School 12 16-08-2021 HOOGHLY HARIPAL JEJUR Jejur High School Bankagacha Nanilal Ghosh Nimno 13 16-08-2021 HOOGHLY CHANDITALA-2 NAITI Buniadi Vidyalaya 14 16-08-2021 HOOGHLY PURSHURA SHYAMPUR Shyampur High School 15 16-08-2021 HOOGHLY POLBA-DADPUR SATITHAN Nabagram Pry School 16 16-08-2021 HOOGHLY JANGIPARA ANTPUR Antpur High School 17 16-08-2021 HOOGHLY PANDUA SIMLAGARHVITASIN Talbona Radharani Girls High School 18 16-08-2021 HOOGHLY PANDUA SIMLAGARHVITASIN Ranagarh High School SRI RAMKRISHNA SARADA VIDYA 19 16-08-2021 HOOGHLY GOGHAT-2 KAMARPUKUR MAHAPITHA Ward - 017,Ward - 018,Ward - PALBAGAN DURGA MANDIR ARABINDA 20 16-08-2021 HOOGHLY Bhadreswar (M) 019,Ward - 020 SARANI PARUL RAMKRISHNA SARADA HIGH 21 16-08-2021 HOOGHLY Arambagh (M) Ward - 001,Ward - 002 SCHOOL 22 16-08-2021 HOOGHLY CHANDITALA-1 AINYA Akuni B.G. -

Women's Empowerment and Micro-Finance Programmesapproaches, Evidence and Ways Forward
..........._....___......_.................LIBRARY 1 JULoitik 1 ,.i41 FOUNDATiON OF AGRICULTURAl. ECONOM!C' Women's Empowerment and Micro-Finance ProgrammesApproaches, Evidence and Ways Forward Linda Mayoux DPP Working Paper No 41 Development Policy and Practice Research Group Faculty of Technology The Open University July 1998 Women's Empowerment and Micro-Finance ProgrammesApproaches, Evidence and Ways Forward by Linda Mayoux DPP Working Paper No 41 1 PREFACE This paper is based on workshop discussions and material collated during a pilot research project entitled 'Micro-Finance Programmes and Women's Empowerment: Strategies for Increasing Impact'. The project was funded by the Small Enterprise Development Fund, ODA UK(now DfID) and sponsored by a steering committee of UK-based NGOs headed by Action Aid and including ACORD,CAFOD, CARE -International, Christian Aid, Friends of ASSEFA, Oxfam, Opportunity Trust, Save the Children, WOMANKIND and World Vision. Workshops were hosted by Action Aid in Ethiopia (January 13th-15th 1997) for East Africa region, India (April 9th to 11th 1997)for South Asia region and Ghana (April 28th to 30th 1997) for West Africa region. A grant from HIVOS enabled substantial revision of the original draft as Background paper to a fourth workshop in Harare March 1998 funded by HIVOS and participating organizations and hosted by Opportunity Trust. I would like to thank all the organizations who took part in the pilot study for their enthusiasm and generous sharing of information. I am particularly grateful to Susan Johnson of Action Aid for co- ordinating the project so professionally and her continual support and guidance through the literature, to Mary Locke of Opportunity Trust, Kate Young of WOMANKIND, Mavis Owusu-Gyamfi and Orlanda Ruthven of SEDF/DfID for their comments on earlier papers and to the many other NGO and staff who assisted the project in various ways. -

And the Liminality of Foreign Merchants
‘Tribute Exchange’ and the Liminality of Foreign Merchants in Mukunda’s Candimangal* Introduction. This essay is about the way merchants and their activities have been imagined in a Bengali poem of the sixteenth century, Candimangal by Mukunda, probably written in the second half of the sixteenth century.1 The author was a Brahman. Mukunda wrote with the patronage of the Brahman ruler of Brahmanbhum, in what now was undivided Midnapur * An earlier version of this paper was presented to a panel on mediaeval Bengali literature at the 34th International Congress of Asian and North African Studies, Hong Kong, on August 28, 1993. I would like to thank the organiser of the panel, Rahul Peter Das, and a participant, William L. Smith, for their comments and questions. I also would like to thank the American Institute of Indian Studies for a Senior Fellowship which supported this work at its inception in 1982/83. (Medinipur) District, West Bengal, and then was a frontier region in the northernmost marches of Orissa. The poet himself, however, came to Brahmanbhum from a village near the town of Burdwan (Barddhaman), some 30 miles west of the Hugli River, in the heart of the long-settled country of the Rarh.2 Mukunda's poem became well known throughout Bengal. For three centuries it was recited, and in the process added to and revised, in the courts of ‘little kingdoms’3 and in the courtyards of important families on the occasion of the annual celebration of Durga- puja. Merchants play a central role in Mukunda’s poem, especially in its final narrative. -

ELECTION COMMISSION of INDIA Nirvachan Sad An, Ashoka Road, New Dolhi-T Loom
URGENT " HEADQUARTERS EMPLOYEES' STATE INSURANCE CORPORATION PANCHDEEP BHAVAN: C.I.G. ROAD:NEW DELHI-ll0002. http://esic.nic.in No. Z-17/12/2/2007-(Misc-3)-E.I Dated: 30.03.2011 MEMORANDUM Sub:- Schedule for General Election to State Legislative Assemblies of Assam, Kerala, Tamil Nadu, West Bengal and Puducherry- Enforcement of model code of conduct. Pleasefind enclosed the copy of letter bearing No. Z-11020/1/2011-Coord. dated 16.03.2011 received from Govt. of India, Ministry of Labour & Employment, Shram Shakti Bhawan, New Delhi alongwith its enclosures on the above cited subject for information & compliance and circulate to all subordinate offices. Encl.: As above Copy to:- 1. All Regional Directors/Joint Director -I/cs/ Director -I/cs, Assam, Kerala, Tamil Nadu, West Bengal and Puducherry. 2. All the Medical Superintendent of ESICHospitals/Model Hospitals, Assam, Kerala, Tamil Nadu, West Bengal and Puducherry. 3. All the SMC/SSMCof ESIC,Assam, Kerala, Tamil Nadu, West Bengal and Puducherry. 4. Joint Director-V for information. 5. Guard File/ Spare Copies. ~ Sh. Pranava Kumar, Assistant Director, Hqrs. with the request to upload a . copy of Memo. in our website. No.Z-11020/1/2011-Coord. Government of India/ Bharat Sarkar Ministry of Labour and Employment ( Shram aur Rozgar Mantralaya) ( Coordination Section) ********* Shram Shakti Bhavan, Rafi Marg, New Delhi, the 16th March, 2011 NOTE Subject: Schedule for General Election to State Legislative Assemblies of Assam, Kerala, Tamil Nadu, West _I'-.@;ngar'andPudducherry - Enforcement of model code of conduct - Circulation regarding. A copy of O.M. No.IV/ 14015/2/2011-CSR-II dated 09th March, 2011 received from Ministry of Home Affairs (C.S.Division) on the above subject is enclosed for information, guidance and appropriate action. -

193-Saptagram Assembly Constituency
FORM 77A See rule 10(1)] LIST OF CONTESTING CANDIDATES Election to the 193-Saptagram Assembly constituency. S. Symbol Name of candidate Address of candidates @Party No. affiliation Allotted 1 4 ()Candidates of recognised National and State Political Parties 1/2, PURBASHA FLAT PHULPUKUR ALL INDIA 1 TAPAN DASGUPTA TRINAMOOL ROAD, P.O.-CHINSURAH, DIST. FLOWERS & HOOGHLY, PIN-712101 CONGRES GRASS CHOTO KHEJURIYA, DEBABRATTA ADCONAGAR, P.S-MOGRA, BHARATIYA 2 BISWAS DIST- HOOGHLY, PIN- 712121 JANATA LOTUS PARTY CHANDRAHATI MADHUSUDANPUR, P.O- PABITRA DEB CHANDRAHATI, P.S- MoGRA, DIST- INDIAN HAND HOOGHLY, PIN-712504 NATIONAL CONGRESS i) Candidates of registered political parties (other than recognised National and State Political Parties). NIL NIL NIL NIL NIL NING Cenerai Eeciion VVBIA Returning Officer 2021 193, Saptagram A. C. 93C2nt DGO 1 f er candidates @Party Name of candidate Address of candidates affiliation 3 4 5 ADISAPTAGRAM SARASATIPARA, AJOY DAS P.O&P.S.-MAGRA, DIST. 4. INDEPENDENT HAT HOOGHLY, PIN-712148 SUBHASHPALLY, PARITOSH P.O.-BANSBERIA, P.S.-MAGRA, INDEPENDENT BUCKET 5. KARMAKAR DIST HOGHLY, PIN-712502 HAZRA PARA,20, BANSBERIA, BISHNU PEN NIB WITH MAGRA, HOOGHLY, 712503 INDEPENDENT 6. CHOWDHURI SEVEN RAYS CHOTO KHEJURIYA, ADCONAGAR, P.S-MOGRA, DIST- HOOGHLY, PIN- MILAN DAS INDEPENDENT FOOTBALL 7. 712121 PALPARA, ADISAPTAGRAM, P.O &P.S.- MAGRA, DIST. SUBIR ROOY HOOGHLY, INDEPENDENT DIESEL PUMP 8. PIN-712148 Ceneral Returning Officer 201 Eection C. Officer A A. Returning Place Chinsurah WBLA 193, Saptagram 2021 193-Saptagram Assembly Constituency Date 26.03.2021 and above. in the case of candidates mentioned under categories (i) (ii) Applicable the three categories shall be given N.B.-Under Col.1 above, the serial numbers of candidates of all consecutively and not separately for each category. -

Influence of the River Ganga on the Urban Process in Kolkata Metropolitan Area
IOSR Journal Of Humanities And Social Science (IOSR-JHSS) Volume 19, Issue 9, Ver. VI (Sep. 2014), PP 60-67 e-ISSN: 2279-0837, p-ISSN: 2279-0845. www.iosrjournals.org Influence of the River Ganga on the Urban Process in Kolkata Metropolitan Area Dr. Sarbendu Bikash Dhar Hindu School, Kolkata, India Abstract : From the dawn of human civilization, rivers have been playing a significant role for the development of human settlement worldwide. The Kolkata Metropolitan Area (KMA) is no exception to this. It is located on the bank of river Hugli, the distributory of river Ganga at its lower course in India. In the medieval and early modern period it was the most important riverine trade route in eastern India when market based economy was started to develop. In the later phase Kolkata (erstwhile Calcutta) port and adjoining town was established. Afterwards, this port town expanded rapidly to become the metropolitan city of Kolkata, which was the national capital of British India till 1911and became the main center of economic, cultural and political activities in the country. Following the partition and independence of India, a phenomenal change in the population distribution took place as a result of huge refugee influx from erstwhile East Pakistan, now Bangladesh. At that time river Hugli acted as a major barrier of migration flow between the eastern and western districts of KMA. Even today, effects of such immigration are reflected through population pressure differential on both the banks within KMA. Apart from that, the land use and morphology of this metropolis is also profoundly affected by the existence of river Hugli. -
The Adi Ganga
ISSN (Online) - 2349-8846 The Adi Ganga A Forgotten River in Bengal JENIA MUKHERJEE Vol. 51, Issue No. 8, 20 Feb, 2016 Jenia Mukherjee ([email protected]) teaches at the Institute of Development Studies, Kolkata. The article sheds light on the Adi Ganga, one of the most significant streams of the Ganges in its lower course, and narrates how the stream (later Tolly’s Canal) which was once the life line of Kolkata transformed into a mere sewer and was ruthlessly slaughtered with the changing politico-economic interests of the state. Introduction Cities and civilisations flourished on the banks of rivers, rivulets, canals and creeks—popularly known as “riverine ecology.” The relationship between wo(man) and nature was that of mutual interdependence. This continued till capitalism commodified labour and transformed the sustainable relationship between the social and ecological to “metabolic rift” in Marxist terms (Foster 2000). This economic system ensured that nature was commodified in keeping with the politico-economic interests of the state. Within this framework, the article studies the Adi Ganga, one of the significant streams of the Hooghly River across historical trajectories since the pre-colonial to the present times. Using a political ecology approach it traces the shift in development perspectives that determined the fate of the stream in colonial and postcolonial Kolkata. The Present Situation of the Canal One cannot miss the sight and foul smell of a polluted water tract beneath Alipur bridge on the way to the National Library or while travelling from Naktala to Garia in the southern part of Kolkata. This water tract is none other than the Tolly’s Canal which was part of the old route of the Adi Ganga revived by William Tolly between 1772 and 1777. -

West Bengal Act XIII of 1966 •
• West Bengal Act XIII of 1966 THE CALCUTTA METROPOLItat AND SANITATION AUTHORITY ACT, 1966. [Passed by the West Bengal Legislature.] [Assent of the President was first published in the Calcutta. Gazette, Extraordinary, of the 26th May, 1966.] [26th May, 1966.] An Act to provide for the establishment of an Authority for the maintenance, development and regulation of water-supply, sewerage and drainage services and for the collection and disposal of garbage in the Calcutta Metropolitan District with a view to the promotion of public health and for matters connected therewith. WHEREAS it is expedient to provide for the establishment of an Authority for the maintenance, development and regulation cif water-supply, sewerage and drainage services and for the collection and disposal of garbage in the Calcutta Metropolitan. District with a view to the promotion of public health and for matters connected therewith; It is hereby enacted. in the Sixteenth Year of the Republic of India, by the Legislature of West Bengal, as follows:— CHAPTER I. • - PRELIMINARY. _ (1) This Act-may be called the Calcutta Metropolitan Short title, Water and Sanitation Authority Act, 1966, extent and Commence. (2) It extends to the Calcutta Metropolitan District exclud- ment. ing any cantonment or part of a cantonment within the said District. It shall come is force at: oco. Z. (1) In 'this Act unless there is anything repugnant in befini thniNect ar context,- - Hone. (a) Authority' means the Calcutta Metropolitan Water and Sanitation Authority established under section _ 3; • (b) "Board" means the Board of Directors mentioned in section 4; • or "District" means the area estoribed in. -

List of Polling Station- WBLA-2021
List of Polling Station- WBLA-2021 AC Name Serial No Locality of polling station Building in which it will be located Polling Areas Najrul Shatabarshiki Prathamik 185 1 Vill- Basai 1) Basai Colony Vidyalaya- Room-1 Najrul Shatabarshiki Prathamik 185 2 Vill- Basai Basai Colony Vidyalaya- Room-2 185 3 Vill- Basai Gaspel Home Bidyalaya-Room-1 Basai Colony 185 4 Vill- Basai Gaspel Home Bidyalaya-Room-2 Basai Colony Bipin Behari Smriti Prathamik 185 5 Vill- Basai 1)Basai (West) Bidyalaya-Room-1 Bipin Behari Smriti Prathamik 185 6 Vill- Basai 1)Basai (North) (01 - 787) Bidyalaya-Room-2 Bipin Behari Smriti Prathamik 185 6A Vill- Basai 1)Basai (North) (788 - 1418) Bidyalaya -Room-2A 185 7 Vill- Kanaipur, Kanaipur High School, Room-1 Kanaipur East 185 8 Vill- Kanaipur, Kanaipur High School, Room-2 Kanaipur East 185 9 Vill- Kanaipur, Kanaipur High School, Room-3 (1) Naity Road, 2) Harisabha(388-660) 185 9A Vill- Kanaipur, Kanaipur High School, Room-3A 2) Harisabha (661-1326) (1) Ganganagar ( 2) Harisabha (496- 185 10 Vill- Kanaipur, Kanaipur High School, Room-4 598) 185 10A Vill- Kanaipur, Kanaipur High School, Room-4A ( 2) Harisabha (599-1153) Page 1 of 508 AC Name Serial No Locality of polling station Building in which it will be located Polling Areas (1) Kanaipur (2) Kanaipur Colony (3) 185 11 Vill- Kanaipur, Nanilal Pry. Vidyalaya, Room-1 Kanaipur Noyapara Abaitanik Pry. Vidyalaya, 185 12 Vill -Noapara Noyapara ( East ) (1 - 614) Room-1 Noyapara Abaitanik Pry. Vidyalaya, 185 12A Vill -Noapara Noyapara ( East ) (615 - 1210) Room-1A Noyapara Abaitanik Pry. -

2017-18 Government of West Bengal Office of The
2017-18 GOVERNMENT OF WEST BENGAL OFFICE OF THE DISTRICT MAGISTRATE AND COLLECTOR HOOGHLY DEPARTMENT OF DISASTER MANAGEMENT 1 INDEX DISASTER MANAGEMENT PLAN, HOOGHLY 2017-18 CONTENTS PAGE NO. 1) Foreword 3 2) Disaster Management Map of Hooghly Dist. 4 3) Map of Flood Prone areas 4 4) Flood Shelter Map 4 5) District Profile 6) Resolution of Disaster Management Preparedness 7 Meeting 7) Photographs of Review Meeting 10 8) Disaster Management and Overview 13 9) Important Contact Number and District Profile 15 10) Identification of Vulnerable Areas 28 11) List of Embankments 31 12) Status report of Relief Godown 31 13) Status report of Flood Shelter 34 14) Line Department I) P.H.E. Department 36 II) Animal Resources Department 40 III) Food Supply Department 44 iv) Health & Family Welfare Department 52 V) Civil Defence 54 VI) Agriculture Department 56 VII) Fisharies Department 61 VIII) Fire Brigade. 64 IX) WBSEDCL 65 15) Sub-Divisional Planning I) Arambag Sub-Division 66 II) Chandernagore Sub-Divison 162 III) Serampore Sub-Division 189 124 IV) Sadar Sub Division 228 2 F O R E W O R D The district of Hooghly has been identified as the plan district in view to its vulnerability to major natural and man-made disasters such as flood, draught, cyclone, fire etc. The natural disasters especially cyclones and floods affect this district every year. This distsrict experienced flood in the month of July, -August, 2015. The incessant and heavy rainfall and the consequent copious discharge of water from different barrage/dam hugely disturb the normal life in the catchment areas resulting in huge loss of life and property. -

DECAY of SARASWATI RIVER with SPECIAL EMPHASIS on ITS ENVIRONMENTAL ISSUES HOOGHLY & HOWRAH DISTRICT, WEST BENGAL Basanta Mandal M.Sc
|| Volume 2 || Issue 5 || 2017 || ISSN (Online) 2456-3293 DECAY OF SARASWATI RIVER WITH SPECIAL EMPHASIS ON ITS ENVIRONMENTAL ISSUES HOOGHLY & HOWRAH DISTRICT, WEST BENGAL Basanta Mandal M.Sc. in Department of Geography, Presidency University, Kolakata [email protected] ------------------------------------------------------------------------------------------------------------ Abstract: These days each study is giving emphasis in its applied aspect. In this respect the application of fluvial geomorphology in resource management is essential. Dying river and flood prone areas are common features present in deltaic tracts of river; the changing nature of decaying rivers has important effect upon the cultural landscape. Land utilization changes and population dynamics accompany. Changes happen in floodplains and in deltas. Such areas have greater concentration of population. Therefore, any change in the natural aspect will have important effects on human activities. Rivers, which were once large and navigable, undergo silting up and decay. With time, they degenerate into insignificant streams. Ports may have developed along them in the past. River water may have been utilized for agriculture. Hence population may have concentrated along them. But, with the decay of such rivers, ports disappeared, agriculture declined in importance and the tendency to attract population decrease. The inter riverine tracts are not build up. So they decay to form low-lying flood prone tracts. Water logging becomes constant problem. Considering all these facts the present research has been organized on Sara Swati River, West Bengal Keywords: River system, Micro level analysis of Devanandapur mouza, change in river morphology, Problem aspect, Management aspect. -------------------------------------------------------------------------------------------------------- I INTRODUCTION Pollution from various sources is entering the river. The research has tried to identify these problems, along selected Saraswati River was a distributary of the Bhagirathi.