Chaos and Providence
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Title: Fractals Topics: Symmetry, Patterns in Nature, Biomimicry Related Disciplines: Mathematics, Biology Objectives: A. Learn
Title: Fractals Topics: symmetry, patterns in nature, biomimicry Related Disciplines: mathematics, biology Objectives: A. Learn about how fractals are made. B. Think about the mathematical processes that play out in nature. C. Create a hands-on art project. Lesson: A. Introduction (20 minutes) Fractals are sets in mathematics based on repeated processes at different scales. Why do we care? Fractals are a part of nature, geometry, algebra, and science and are beautiful in their complexity. Fractals come in many types: branching, spiral, algebraic, and geometric. Branching and spiral fractals can be found in nature in many different forms. Branching is seen in trees, lungs, snowflakes, lightning, and rivers. Spirals are visible in natural forms such as hurricanes, shells, liquid motion, galaxies, and most easily visible in plants like flowers, cacti, and Romanesco Figure 1: Romanesco (Figure 1). Branching fractals emerge in a linear fashion. Spirals begin at a point and expand out in a circular motion. A cool demonstration of branching fractals can be found at: http://fractalfoundation.org/resources/what-are-fractals/. Algebraic fractals are based on surprisingly simple equations. Most famous of these equations is the Mandelbrot Set (Figure 2), a plot made from the equation: The most famous of the geometric fractals is the Sierpinski Triangle: As seen in the diagram above, this complex fractal is created by starting with a single triangle, then forming another inside one quarter the size, then three more, each one quarter the size, then 9, 27, 81, all just one quarter the size of the triangle drawn in the previous step. -

Complexity” Makes a Difference: Lessons from Critical Systems Thinking and the Covid-19 Pandemic in the UK
systems Article How We Understand “Complexity” Makes a Difference: Lessons from Critical Systems Thinking and the Covid-19 Pandemic in the UK Michael C. Jackson Centre for Systems Studies, University of Hull, Hull HU6 7TS, UK; [email protected]; Tel.: +44-7527-196400 Received: 11 November 2020; Accepted: 4 December 2020; Published: 7 December 2020 Abstract: Many authors have sought to summarize what they regard as the key features of “complexity”. Some concentrate on the complexity they see as existing in the world—on “ontological complexity”. Others highlight “cognitive complexity”—the complexity they see arising from the different interpretations of the world held by observers. Others recognize the added difficulties flowing from the interactions between “ontological” and “cognitive” complexity. Using the example of the Covid-19 pandemic in the UK, and the responses to it, the purpose of this paper is to show that the way we understand complexity makes a huge difference to how we respond to crises of this type. Inadequate conceptualizations of complexity lead to poor responses that can make matters worse. Different understandings of complexity are discussed and related to strategies proposed for combatting the pandemic. It is argued that a “critical systems thinking” approach to complexity provides the most appropriate understanding of the phenomenon and, at the same time, suggests which systems methodologies are best employed by decision makers in preparing for, and responding to, such crises. Keywords: complexity; Covid-19; critical systems thinking; systems methodologies 1. Introduction No one doubts that we are, in today’s world, entangled in complexity. At the global level, economic, social, technological, health and ecological factors have become interconnected in unprecedented ways, and the consequences are immense. -

Branching in Nature Jennifer Welborn Amherst Regional Middle School, [email protected]
University of Massachusetts Amherst ScholarWorks@UMass Amherst Patterns Around Us STEM Education Institute 2017 Branching in Nature Jennifer Welborn Amherst Regional Middle School, [email protected] Wayne Kermenski Hawlemont Regional School, [email protected] Follow this and additional works at: https://scholarworks.umass.edu/stem_patterns Part of the Biology Commons, Physics Commons, Science and Mathematics Education Commons, and the Teacher Education and Professional Development Commons Welborn, Jennifer and Kermenski, Wayne, "Branching in Nature" (2017). Patterns Around Us. 2. Retrieved from https://scholarworks.umass.edu/stem_patterns/2 This Article is brought to you for free and open access by the STEM Education Institute at ScholarWorks@UMass Amherst. It has been accepted for inclusion in Patterns Around Us by an authorized administrator of ScholarWorks@UMass Amherst. For more information, please contact [email protected]. Patterns Around Us: Branching in Nature Teacher Resource Page Part A: Introduction to Branching Massachusetts Frameworks Alignment—The Nature of Science • Overall, the key criterion of science is that it provide a clear, rational, and succinct account of a pattern in nature. This account must be based on data gathering and analysis and other evidence obtained through direct observations or experiments, reflect inferences that are broadly shared and communicated, and be accompanied by a model that offers a naturalistic explanation expressed in conceptual, mathematical, and/or mechanical terms. Materials: -

Art on a Cellular Level Art and Science Educational Resource
Art on a Cellular Level Art and Science Educational Resource Phoenix Airport Museum Educators and Parents, With foundations in art, geometry and plant biology, the objective of this lesson is to recognize patterns and make connections between the inexhaustible variety of life on our planet. This educational resource is geared for interaction with students of all ages to support the understanding between art and science. It has been designed based on our current exhibition, Art on a Cellular Level, on display at Sky Harbor. The questions and activities below were created to promote observation and curiosity. There are no wrong answers. You may print this PDF to use as a workbook or have your student refer to the material online. We encourage educators to expand on this art and science course to create a lesson plan. If you enjoy these activities and would like to investigate further, check back for new projects each week (three projects total). We hope your student will have fun with this and make an art project to share with us. Please send an image of your student’s artwork to [email protected] or hashtag #SkyHarborArts for an opportunity to be featured on Phoenix Sky Harbor International Airport’s social media. Art on a Cellular Level exhibition Sky Harbor, Terminal 4, level 3 Gallery Art is a lens through which we view the world. It can be a tool for storytelling, expressing cultural values and teaching fundamentals of math, technology and science in a visual way. The Terminal 4 gallery exhibition, Art on a Cellular Level, examines the intersections between art and science. -

Role of Nonlinear Dynamics and Chaos in Applied Sciences
v.;.;.:.:.:.;.;.^ ROLE OF NONLINEAR DYNAMICS AND CHAOS IN APPLIED SCIENCES by Quissan V. Lawande and Nirupam Maiti Theoretical Physics Oivisipn 2000 Please be aware that all of the Missing Pages in this document were originally blank pages BARC/2OOO/E/OO3 GOVERNMENT OF INDIA ATOMIC ENERGY COMMISSION ROLE OF NONLINEAR DYNAMICS AND CHAOS IN APPLIED SCIENCES by Quissan V. Lawande and Nirupam Maiti Theoretical Physics Division BHABHA ATOMIC RESEARCH CENTRE MUMBAI, INDIA 2000 BARC/2000/E/003 BIBLIOGRAPHIC DESCRIPTION SHEET FOR TECHNICAL REPORT (as per IS : 9400 - 1980) 01 Security classification: Unclassified • 02 Distribution: External 03 Report status: New 04 Series: BARC External • 05 Report type: Technical Report 06 Report No. : BARC/2000/E/003 07 Part No. or Volume No. : 08 Contract No.: 10 Title and subtitle: Role of nonlinear dynamics and chaos in applied sciences 11 Collation: 111 p., figs., ills. 13 Project No. : 20 Personal authors): Quissan V. Lawande; Nirupam Maiti 21 Affiliation ofauthor(s): Theoretical Physics Division, Bhabha Atomic Research Centre, Mumbai 22 Corporate authoifs): Bhabha Atomic Research Centre, Mumbai - 400 085 23 Originating unit : Theoretical Physics Division, BARC, Mumbai 24 Sponsors) Name: Department of Atomic Energy Type: Government Contd...(ii) -l- 30 Date of submission: January 2000 31 Publication/Issue date: February 2000 40 Publisher/Distributor: Head, Library and Information Services Division, Bhabha Atomic Research Centre, Mumbai 42 Form of distribution: Hard copy 50 Language of text: English 51 Language of summary: English 52 No. of references: 40 refs. 53 Gives data on: Abstract: Nonlinear dynamics manifests itself in a number of phenomena in both laboratory and day to day dealings. -
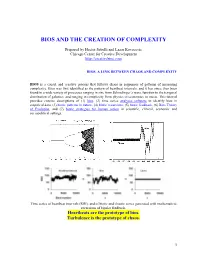
Bios and the Creation of Complexity
BIOS AND THE CREATION OF COMPLEXITY Prepared by Hector Sabelli and Lazar Kovacevic Chicago Center for Creative Development http://creativebios.com BIOS, A LINK BETWEEN CHAOS AND COMPLEXITY BIOS is a causal and creative process that follows chaos in sequences of patterns of increasing complexity. Bios was first identified as the pattern of heartbeat intervals, and it has since then been found in a wide variety of processes ranging in size from Schrodinger’s wave function to the temporal distribution of galaxies, and ranging in complexity from physics to economics to music. This tutorial provides concise descriptions of (1) bios, (2) time series analyses software to identify bios in empirical data, (3) biotic patterns in nature, (4) biotic recursions, (5) biotic feedback, (6) Bios Theory of Evolution, and (7) biotic strategies for human action in scientific, clinical, economic and sociopolitical settings. Time series of heartbeat intervals (RRI), and of biotic and chaotic series generated with mathematical recursions of bipolar feedback. Heartbeats are the prototype of bios. Turbulence is the prototype of chaos. 1 1. BIOS BIOS is an expansive process with chaotic features generated by feedback and characterized by features of creativity. Process: Biotic patterns are sequences of actions or states. Expansive: Biotic patterns continually expand in their diversity and often in their range. This is significant, as natural processes expand, in contrast to convergence to equilibrium, periodic, or chaotic attractors. Expanding processes range from the universe to viruses, and include human populations, empires, ideas and cultures. Chaotic: Biotic series are aperiodic and generated causally; mathematically generated bios is extremely sensitive to initial conditions. -

Annotated List of References Tobias Keip, I7801986 Presentation Method: Poster
Personal Inquiry – Annotated list of references Tobias Keip, i7801986 Presentation Method: Poster Poster Section 1: What is Chaos? In this section I am introducing the topic. I am describing different types of chaos and how individual perception affects our sense for chaos or chaotic systems. I am also going to define the terminology. I support my ideas with a lot of examples, like chaos in our daily life, then I am going to do a transition to simple mathematical chaotic systems. Larry Bradley. (2010). Chaos and Fractals. Available: www.stsci.edu/~lbradley/seminar/. Last accessed 13 May 2010. This website delivered me with a very good introduction into the topic as there are a lot of books and interesting web-pages in the “References”-Sektion. Gleick, James. Chaos: Making a New Science. Penguin Books, 1987. The book gave me a very general introduction into the topic. Harald Lesch. (2003-2007). alpha-Centauri . Available: www.br-online.de/br- alpha/alpha-centauri/alpha-centauri-harald-lesch-videothek-ID1207836664586.xml. Last accessed 13. May 2010. A web-page with German video-documentations delivered a lot of vivid examples about chaos for my poster. Poster Section 2: Laplace's Demon and the Butterfly Effect In this part I describe the idea of the so called Laplace's Demon and the theory of cause-and-effect chains. I work with a lot of examples, especially the famous weather forecast example. Also too I introduce the mathematical concept of a dynamic system. Jeremy S. Heyl (August 11, 2008). The Double Pendulum Fractal. British Columbia, Canada. -

Chaos Theory and Its Application to Education: Mehmet Akif Ersoy University Case*
Educational Sciences: Theory & Practice • 14(2) • 510-518 ©2014 Educational Consultancy and Research Center www.edam.com.tr/estp DOI: 10.12738/estp.2014.2.1928 Chaos Theory and its Application to Education: Mehmet Akif Ersoy University Case* Vesile AKMANSOYa Sadık KARTALb Burdur Provincial Education Department Mehmet Akif Ersoy University Abstract Discussions have arisen regarding the application of the new paradigms of chaos theory to social sciences as compared to physical sciences. This study examines what role chaos theory has within the education process and what effect it has by describing the views of university faculty regarding chaos and education. The partici- pants in this study consisted of 30 faculty members with teaching experience in the Faculty of Education, the Faculty of Science and Literature, and the School of Veterinary Sciences at Mehmet Akif Ersoy University in Burdur, Turkey. The sample for this study included voluntary participants. As part of the study, the acquired qualitative data has been tested using both the descriptive analysis method and content analysis. Themes have been organized under each discourse question after checking and defining the processes. To test the data, fre- quency and percentage, statistical techniques were used. The views of the attendees were stated verbatim in the Turkish version, then translated into English by the researchers. The findings of this study indicate the presence of a “butterfly effect” within educational organizations, whereby a small failure in the education process causes a bigger failure later on. Key Words Chaos, Chaos and Education, Chaos in Social Sciences, Chaos Theory. The term chaos continues to become more and that can be called “united science,” characterized by more prominent within the various fields of its interdisciplinary approach (Yeşilorman, 2006). -

The Edge of Chaos – an Alternative to the Random Walk Hypothesis
THE EDGE OF CHAOS – AN ALTERNATIVE TO THE RANDOM WALK HYPOTHESIS CIARÁN DORNAN O‟FATHAIGH Junior Sophister The Random Walk Hypothesis claims that stock price movements are random and cannot be predicted from past events. A random system may be unpredictable but an unpredictable system need not be random. The alternative is that it could be described by chaos theory and although seem random, not actually be so. Chaos theory can describe the overall order of a non-linear system; it is not about the absence of order but the search for it. In this essay Ciarán Doran O’Fathaigh explains these ideas in greater detail and also looks at empirical work that has concluded in a rejection of the Random Walk Hypothesis. Introduction This essay intends to put forward an alternative to the Random Walk Hypothesis. This alternative will be that systems that appear to be random are in fact chaotic. Firstly, both the Random Walk Hypothesis and Chaos Theory will be outlined. Following that, some empirical cases will be examined where Chaos Theory is applicable, including real exchange rates with the US Dollar, a chaotic attractor for the S&P 500 and the returns on T-bills. The Random Walk Hypothesis The Random Walk Hypothesis states that stock market prices evolve according to a random walk and that endeavours to predict future movements will be fruitless. There is both a narrow version and a broad version of the Random Walk Hypothesis. Narrow Version: The narrow version of the Random Walk Hypothesis asserts that the movements of a stock or the market as a whole cannot be predicted from past behaviour (Wallich, 1968). -

Strategies and Rubrics for Teaching Chaos and Complex Systems Theories As Elaborating, Self-Organizing, and Fractionating Evolutionary Systems Lynn S
Strategies and Rubrics for Teaching Chaos and Complex Systems Theories as Elaborating, Self-Organizing, and Fractionating Evolutionary Systems Lynn S. Fichter1,2, E.J. Pyle1,3, S.J. Whitmeyer1,4 ABSTRACT To say Earth systems are complex, is not the same as saying they are a complex system. A complex system, in the technical sense, is a group of ―agents‖ (individual interacting units, like birds in a flock, sand grains in a ripple, or individual units of friction along a fault zone), existing far from equilibrium, interacting through positive and negative feedbacks, forming interdependent, dynamic, evolutionary networks, that possess universality properties common to all complex systems (bifurcations, sensitive dependence, fractal organization, and avalanche behaviour that follows power- law distributions.) Chaos/complex systems theory behaviors are explicit, with their own assumptions, approaches, cognitive tools, and models that must be taught as deliberately and systematically as the equilibrium principles normally taught to students. We present a learning progression of concept building from chaos theory, through a variety of complex systems, and ending with how such systems result in increases in complexity, diversity, order, and/or interconnectedness with time—that is, evolve. Quantitative and qualitative course-end assessment data indicate that students who have gone through the rubrics are receptive to the ideas, and willing to continue to learn about, apply, and be influenced by them. The reliability/validity is strongly supported by open, written student comments. INTRODUCTION divided into fractions through the addition of sufficient Two interrelated subjects are poised for rapid energy because of differences in the size, weight, valence, development in the Earth sciences. -

Pattern Formation in Nature: Physical Constraints and Self-Organising Characteristics
Pattern formation in nature: Physical constraints and self-organising characteristics Philip Ball ________________________________________________________________ Abstract The formation of patterns is apparent in natural systems ranging from clouds to animal markings, and from sand dunes to the intricate shells of microscopic marine organisms. Despite the astonishing range and variety of such structures, many seem to have analogous features: the zebra’s stripes put us in mind of the ripples of blown sand, for example. In this article I review some of the common patterns found in nature and explain how they are typically formed through simple, local interactions between many components of a system – a form of physical computation that gives rise to self- organisation and emergent structures and behaviours. ________________________________________________________________ Introduction When the naturalist Joseph Banks first encountered Fingal’s Cave on the Scottish island of Staffa, he was astonished by the quasi-geometric, prismatic pillars of rock that flank the entrance. As Banks put it, Compared to this what are the cathedrals or palaces built by men! Mere models or playthings, as diminutive as his works will always be when compared with those of nature. What now is the boast of the architect! Regularity, the only part in which he fancied himself to exceed his mistress, Nature, is here found in her possession, and here it has been for ages undescribed. This structure has a counterpart on the coast of Ireland: the Giant’s Causeway in County Antrim, where again one can see the extraordinarily regular and geometric honeycomb structure of the fractured igneous rock (Figure 1). When we make an architectural pattern like this, it is through careful planning and construction, with each individual element cut to shape and laid in place. -

Complex Adaptive Systems
Evidence scan: Complex adaptive systems August 2010 Identify Innovate Demonstrate Encourage Contents Key messages 3 1. Scope 4 2. Concepts 6 3. Sectors outside of healthcare 10 4. Healthcare 13 5. Practical examples 18 6. Usefulness and lessons learnt 24 References 28 Health Foundation evidence scans provide information to help those involved in improving the quality of healthcare understand what research is available on particular topics. Evidence scans provide a rapid collation of empirical research about a topic relevant to the Health Foundation's work. Although all of the evidence is sourced and compiled systematically, they are not systematic reviews. They do not seek to summarise theoretical literature or to explore in any depth the concepts covered by the scan or those arising from it. This evidence scan was prepared by The Evidence Centre on behalf of the Health Foundation. © 2010 The Health Foundation Previously published as Research scan: Complex adaptive systems Key messages Complex adaptive systems thinking is an approach that challenges simple cause and effect assumptions, and instead sees healthcare and other systems as a dynamic process. One where the interactions and relationships of different components simultaneously affect and are shaped by the system. This research scan collates more than 100 articles The scan suggests that a complex adaptive systems about complex adaptive systems thinking in approach has something to offer when thinking healthcare and other sectors. The purpose is to about leadership and organisational development provide a synopsis of evidence to help inform in healthcare, not least of which because it may discussions and to help identify if there is need for challenge taken for granted assumptions and further research or development in this area.