A Check for Rational Inattention
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Download the Booklet of Chessbase Magazine #199
THE Magazine for Professional Chess JANUARY / FEBRUARY 2021 | NO. 199 | 19,95 Euro S R V ON U I O D H E O 4 R N U A N DVD H N I T NG RE TIME: MO 17 years old, second place at the Altibox Norway Chess: Alireza Firouzja is already among the Top 20 TOP GRANDmasTERS ANNOTATE: ALL IN ONE: SEMI-TaRRasCH Duda, Edouard, Firouzja, Igor Stohl condenses a Giri, Nielsen, et al. trendy opening AVRO TOURNAMENT 1938 – LONDON SYSTEM – no reST FOR THE Bf4 CLash OF THE GENERATIONS Alexey Kuzmin hits with the Retrospective + 18 newly annotated active 5...Nh5!? Keres games THE MODERN BENONI UNDER FIRE! Patrick Zelbel presents a pointed repertoire with 6.Nf3/7.Bg5 THE MAGAZINE FOR PROFESSIONAL CHESS JANU 17 years old, secondARY / placeFEB at the RU Altibox Norway Chess: AlirezaAR FirouzjaY 2021 is already among the Top 20 NO . 199 1 2 0 2 G R U B M A H , H B M G E S DVD with first class training material for A B S S E club players and professionals! H C © EDITORIAL The new chess stars: Alireza Firouzja and Moscow in order to measure herself against Beth Harmon the world champion in a tournament. She is accompanied by a US official who warns Now the world and also the world of chess her about the Soviets and advises her not to has been hit by the long-feared “second speak with anyone. And what happens? She wave” of the Covid-19 pandemic. Many is welcomed with enthusiasm by the popu- tournaments have been cancelled. -

(2021), 2814-2819 Research Article Can Chess Ever Be Solved Na
Turkish Journal of Computer and Mathematics Education Vol.12 No.2 (2021), 2814-2819 Research Article Can Chess Ever Be Solved Naveen Kumar1, Bhayaa Sharma2 1,2Department of Mathematics, University Institute of Sciences, Chandigarh University, Gharuan, Mohali, Punjab-140413, India [email protected], [email protected] Article History: Received: 11 January 2021; Accepted: 27 February 2021; Published online: 5 April 2021 Abstract: Data Science and Artificial Intelligence have been all over the world lately,in almost every possible field be it finance,education,entertainment,healthcare,astronomy, astrology, and many more sports is no exception. With so much data, statistics, and analysis available in this particular field, when everything is being recorded it has become easier for team selectors, broadcasters, audience, sponsors, most importantly for players themselves to prepare against various opponents. Even the analysis has improved over the period of time with the evolvement of AI, not only analysis one can even predict the things with the insights available. This is not even restricted to this,nowadays players are trained in such a manner that they are capable of taking the most feasible and rational decisions in any given situation. Chess is one of those sports that depend on calculations, algorithms, analysis, decisions etc. Being said that whenever the analysis is involved, we have always improvised on the techniques. Algorithms are somethingwhich can be solved with the help of various software, does that imply that chess can be fully solved,in simple words does that mean that if both the players play the best moves respectively then the game must end in a draw or does that mean that white wins having the first move advantage. -
Draft – Not for Circulation
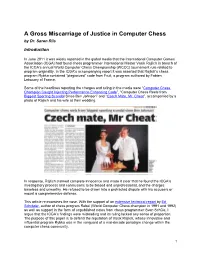
A Gross Miscarriage of Justice in Computer Chess by Dr. Søren Riis Introduction In June 2011 it was widely reported in the global media that the International Computer Games Association (ICGA) had found chess programmer International Master Vasik Rajlich in breach of the ICGA‟s annual World Computer Chess Championship (WCCC) tournament rule related to program originality. In the ICGA‟s accompanying report it was asserted that Rajlich‟s chess program Rybka contained “plagiarized” code from Fruit, a program authored by Fabien Letouzey of France. Some of the headlines reporting the charges and ruling in the media were “Computer Chess Champion Caught Injecting Performance-Enhancing Code”, “Computer Chess Reels from Biggest Sporting Scandal Since Ben Johnson” and “Czech Mate, Mr. Cheat”, accompanied by a photo of Rajlich and his wife at their wedding. In response, Rajlich claimed complete innocence and made it clear that he found the ICGA‟s investigatory process and conclusions to be biased and unprofessional, and the charges baseless and unworthy. He refused to be drawn into a protracted dispute with his accusers or mount a comprehensive defense. This article re-examines the case. With the support of an extensive technical report by Ed Schröder, author of chess program Rebel (World Computer Chess champion in 1991 and 1992) as well as support in the form of unpublished notes from chess programmer Sven Schüle, I argue that the ICGA‟s findings were misleading and its ruling lacked any sense of proportion. The purpose of this paper is to defend the reputation of Vasik Rajlich, whose innovative and influential program Rybka was in the vanguard of a mid-decade paradigm change within the computer chess community. -

Chessbase.Com - Chess News - Grandmasters and Global Growth
ChessBase.com - Chess News - Grandmasters and Global Growth Grandmasters and Global Growth 07.01.2010 Professor Kenneth Rogoff is a strong chess grandmaster, who also happens to be one of the world's leading economists. In a Project Syndicate article that appeared this week Ken sees the new decade as one in which "artificial intelligence hits escape velocity," with an economic impact on par with the emergence of India and China. He uses computer chess to illustrated the point. Grandmasters and Global Growth By Kenneth Rogoff As the global economy limps out of the last decade and enters a new one in 2010, what will be the next big driver of global growth? Here’s betting that the “teens” is a decade in which artificial intelligence hits escape velocity, and starts to have an economic impact on par with the emergence of India and China. Admittedly, my perspective is heavily colored by events in the world of chess, a game I once played at a professional level and still follow from a distance. Though special, computer chess nevertheless offers both a window into silicon evolution and a barometer of how people might adapt to it. A little bit of history might help. In 1996 and 1997, World Chess Champion Gary Kasparov played a pair of matches against an IBM computer named “Deep Blue.” At the time, Kasparov dominated world chess, in the same way that Tiger Woods – at least until recently – has dominated golf. In the 1996 match, Deep Blue stunned the champion by beating him in the first game. -

Determining If You Should Use Fritz, Chessbase, Or Both Author: Mark Kaprielian Revised: 2015-04-06
Determining if you should use Fritz, ChessBase, or both Author: Mark Kaprielian Revised: 2015-04-06 Table of Contents I. Overview .................................................................................................................................................. 1 II. Not Discussed .......................................................................................................................................... 1 III. New information since previous versions of this document .................................................................... 1 IV. Chess Engines .......................................................................................................................................... 1 V. Why most ChessBase owners will want to purchase Fritz as well. ......................................................... 2 VI. Comparing the features ............................................................................................................................ 3 VII. Recommendations .................................................................................................................................... 4 VIII. Additional resources ................................................................................................................................ 4 End of Table of Contents I. Overview Fritz and ChessBase are software programs from the same company. Each has a specific focus, but overlap in some functionality. Both programs can be considered specialized interfaces that sit on top a -

Move Similarity Analysis in Chess Programs
Move similarity analysis in chess programs D. Dailey, A. Hair, M. Watkins Abstract In June 2011, the International Computer Games Association (ICGA) disqual- ified Vasik Rajlich and his Rybka chess program for plagiarism and breaking their rules on originality in their events from 2006-10. One primary basis for this came from a painstaking code comparison, using the source code of Fruit and the object code of Rybka, which found the selection of evaluation features in the programs to be almost the same, much more than expected by chance. In his brief defense, Rajlich indicated his opinion that move similarity testing was a superior method of detecting misappropriated entries. Later commentary by both Rajlich and his defenders reiterated the same, and indeed the ICGA Rules themselves specify move similarity as an example reason for why the tournament director would have warrant to request a source code examination. We report on data obtained from move-similarity testing. The principal dataset here consists of over 8000 positions and nearly 100 independent engines. We comment on such issues as: the robustness of the methods (upon modifying the experimental conditions), whether strong engines tend to play more similarly than weak ones, and the observed Fruit/Rybka move-similarity data. 1. History and background on derivative programs in computer chess Computer chess has seen a number of derivative programs over the years. One of the first was the incident in the 1989 World Microcomputer Chess Cham- pionship (WMCCC), in which Quickstep was disqualified due to the program being \a copy of the program Mephisto Almeria" in all important areas. -

Teaching AI to Play Chess Like People
Teaching AI to Play Chess Like People Austin A. Robinson Division of Science and Mathematics University of Minnesota, Morris Morris, Minnesota, USA 56267 [email protected] ABSTRACT Current chess engines have far exceeded the skill of human players. Though chess is far from being considered a\solved" game, like tic-tac-toe or checkers, a new goal is to create a chess engine that plays chess like humans, making moves that a person in a specific skill range would make and making the same types of mistakes a player would make. In 2020 a new chess engine called Maia was released where through training on thousand of online chess games, Maia was able to capture the specific play styles of players in certain skill ranges. Maia was also able to outperform two of the top chess engines available in human-move prediction, showing that Maia can play more like a human than other chess engines. Figure 1: An example of a blunder made by black when they Keywords moved their queen from the top row to the bottom row indi- Chess, Maia, Human-AI Interaction, Monte Carlo Tree Search, cated by the blue tinted square. This move that allows white Neural Network, Deep Learning to win in one move. If white moves their queen to the top row, than that is checkmate and black loses the game [2]. 1. INTRODUCTION Chess is a problem that computer scientists have been ing chess and concepts related to Deep Learning that will attempting to solve for nearly 70 years now. The first goal be necessary to understand for this paper. -

A Higher Creative Species in the Game of Chess
Articles Deus Ex Machina— A Higher Creative Species in the Game of Chess Shay Bushinsky n Computers and human beings play chess differently. The basic paradigm that computer C programs employ is known as “search and eval- omputers and human beings play chess differently. The uate.” Their static evaluation is arguably more basic paradigm that computer programs employ is known as primitive than the perceptual one of humans. “search and evaluate.” Their static evaluation is arguably more Yet the intelligence emerging from them is phe- primitive than the perceptual one of humans. Yet the intelli- nomenal. A human spectator is not able to tell the difference between a brilliant computer gence emerging from them is phenomenal. A human spectator game and one played by Kasparov. Chess cannot tell the difference between a brilliant computer game played by today’s machines looks extraordinary, and one played by Kasparov. Chess played by today’s machines full of imagination and creativity. Such ele- looks extraordinary, full of imagination and creativity. Such ele- ments may be the reason that computers are ments may be the reason that computers are superior to humans superior to humans in the sport of kings, at in the sport of kings, at least for the moment. least for the moment. This article is about how Not surprisingly, the superiority of computers over humans in roles have changed: humans play chess like chess provokes antagonism. The frustrated critics often revert to machines, and machines play chess the way humans used to play. the analogy of a competition between a racing car and a human being, which by now has become a cliché. -

FIDE Chess Network 1 Introduction
AUSTRIAN JOURNAL OF STATISTICS Volume 40 (2011), Number 4, 225–239 FIDE Chess Network Kristijan Breznik1 and Vladimir Batagelj2 1 International School for Social and Business Studies, Celje, Slovenia 2 Faculty of Mathematics and Physics, Ljubljana, Slovenia Abstract: The game of chess has a long and rich history. In the last century it has been closely connected to the world chess federation FIDE1. This paper analyses all of the rated chess games published on the FIDE website from January 2008 to September 2010 with network analytic methods. We discuss some players and game properties, above all the portion of games played between the world’s best chess players and the frequency of games among countries. Additionally, our analysis confirms the already known advantage of white pieces in the game of chess. We conclude that some modifications in the current system should appear in the near future. Zusammenfassung: Das Schachspiel hat als Spiel eine lange, abwechslungs- reiche Geschichte, die im letzten Jahrhundert mit dem Weltschachbund FIDE eng verbunden ist. In diesem Artikel analysieren wir alle bewerteten und veroffentlichten¨ Spiele der FIDE Webseite von Januar 2008 bis September 2010 unter Verwendung von Netzwerkanalysen. Wir diskutieren einige Spie- ler und die Eigenschaften der Spiele, vor allem den Anteil der Schachspiele zwischen den besten Schachspielern der Welt und die Haufigkeit¨ der Spiele zwischen verschiedenen Landern.¨ Unsere Analyse bestatigt¨ den bekannten Vorteil im Spiel fur¨ denjenigen, der die weißen Figuren besitzt. Schließlich kommen wir zur Feststellung, dass in naher Zukunft einige Veranderungen¨ am aktuellen System verlangt werden sollten. Keywords: Chess, FIDE, Network Analysis, Elo Rating System. -

Learning to Play the Chess Variant Crazyhouse Above World Champion Level with Deep Neural Networks and Human Data Czech, Johannes; Willig, Moritz; Beyer, Alena Et Al
Learning to Play the Chess Variant Crazyhouse Above World Champion Level With Deep Neural Networks and Human Data Czech, Johannes; Willig, Moritz; Beyer, Alena et al. (2020) DOI (TUprints): https://doi.org/10.25534/tuprints-00013370 Lizenz: CC-BY 4.0 International - Creative Commons, Attribution Publikationstyp: Article Fachbereich: 20 Department of Computer Science Quelle des Originals: https://tuprints.ulb.tu-darmstadt.de/13370 ORIGINAL RESEARCH published: 28 April 2020 doi: 10.3389/frai.2020.00024 Learning to Play the Chess Variant Crazyhouse Above World Champion Level With Deep Neural Networks and Human Data Johannes Czech 1*, Moritz Willig 1, Alena Beyer 1, Kristian Kersting 1,2 and Johannes Fürnkranz 3 1 Department of Computer Science, TU Darmstadt, Darmstadt, Germany, 2 Centre for Cognitive Science, TU Darmstadt, Darmstadt, Germany, 3 Department of Computer Science, JKU Linz, Linz, Austria Deep neural networks have been successfully applied in learning the board games Go, chess, and shogi without prior knowledge by making use of reinforcement learning. Although starting from zero knowledge has been shown to yield impressive results, it is associated with high computationally costs especially for complex games. With this Edited by: Balaraman Ravindran, paper, we present CrazyAra which is a neural network based engine solely trained Indian Institute of Technology in supervised manner for the chess variant crazyhouse. Crazyhouse is a game with Madras, India a higher branching factor than chess and there is only limited data of lower quality Reviewed by: Michelangelo Ceci, available compared to AlphaGo. Therefore, we focus on improving efficiency in multiple University of Bari Aldo Moro, Italy aspects while relying on low computational resources. -

The Superstar Effect: Evidence from Chess
The Queen’s Gambit: Explaining the Superstar Effect Using Evidence from Chess * Eren Bilen† Alexander Matros‡ September 24, 2021 Abstract. Superstars exist in classrooms and workplaces. Superstars can either intimidate others by making their peers put in less effort, or they can encourage others by inspiring everybody to “step up” their game. In this study, we analyze direct and indirect effects of a superstar on their peers using evidence from chess. We find that the direct superstar effect is always negative. The indirect superstar effect depends on the intensity of the superstar: if the skill gap between the superstar and the rest is small (large), there is a positive (negative) peer effect. JEL classification: M52, J3, J44, D3 Keywords: superstar, tournament, effort, chess *We would like to thank seminar participants at Dickinson College, Laboratory Innovation Science at Harvard, Lan- caster University, Murray State University, Sabanci University, Southern Illinois University Edwardsville, University of Nebraska Omaha, and University of South Carolina, as well as, participants in the 6th Contests Theory and Evidence conference at the University of East Anglia and the 90th Southern Economic Association Meeting for their questions and suggestions. We thank the Darla Moore School of Business Research Grant Program for the financial support. †Department of Data Analytics, Dickinson College, Carlisle, PA 17013. Email: [email protected] ‡Department of Economics, University of South Carolina, Columbia, SC, 29208. Email: alexan- [email protected] and Department of Economics, Lancaster University, Lancaster, LA1 4YX, United Kingdom. Email: [email protected] 1. Introduction "When you play against Bobby [Fischer], it is not a question of whether you win or lose. -

ECF Enewsletter April 2020
A message from Chessable, sponsors of the ECF eNewsletter --- Must have classic, now available as 19 hours of video, and it's on sale! They are the 100 Endgames You Must Know and there is no quicker, easier and more efficient way to learn them than with this ... the ultimate endgame package on the ultimate chess learning platform. Find out more by following this link April 2020 ECF Newsletter Stay Safe – Play Chess at Home CONTENTS 1 - Play Chess at Home: an update from the ECF 2 - 4NCL Online: All the action from Round 1 3 - ECF Online Events 4 - Join the Club: Where to find your local online chess club 5 - ECF Online Ratings & OTB Monthly Grading 6 - Inside the Chess Bunker: Interview with chess journalist Leon Watson 7 - Tune In, Check Out: Chess podcasts you might like 8 - Chess on YouTube: 8 highly recommended channels 9 - We’ll Meet Again: What you need to know about postponed events 10 - Magnus Carlsen Invitational: $250,000 online rapidplay starts April 18 11 - In Czech: England’s teams at the World Senior Championships in Prague 12 - School’s Out, But Not Chess: CSC online resources for students & tutors 13 - Delancey UK Chess Challenge 14 - ECF Academy Goes Online 15 - ECF Finance Council update 16 – FIDE Veterans Award for Gerry Walsh 17 - Chess Magazine: April 2020 18 – ‘Checkmate Covid-19’ Red Cross Fundraiser 19 - ‘The Chess Pit’ Quiz: 10 brainteasers from the UK’s new chess podcast 1 - Play Chess at Home: An update from the ECF Dear chess friends, Welcome to this unusual April 2020 edition of the ECF Newsletter.