Angular Measure (Degrees, Radians), Arc Length, Π, Angular Speed
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Calculating Growing Degree Days by Jim Nugent District Horticulturist Michigan State University
Calculating Growing Degree Days By Jim Nugent District Horticulturist Michigan State University Are you calculating degree day accumulations and finding your values don't match the values being reported by MSU or your neighbor's electronic data collection unit? There is a logical reason! Three different methods are used to calculate degree days; i.e., 1) Averaging Method; 2) Baskerville-Emin (BE) Method; and 3) Electronic Real-time Data Collection. All methods attempt to calculate the heat accumulation above a minimum threshold temperature, often referred to the base temperature. Once both the daily maximum and minimum temperatures get above the minimum threshold temperature, (i.e., base temperature of 42degrees, 50degrees or whatever other base temperature of interest) then all methods are fairly comparable. However, differences do occur and these are accentuated in an exceptionally long period of cool spring temperatures, such as we experienced this year. Let me briefly explain: 1. Averaging Method: Easy to calculate Degree Days(DD) = Average daily temp. - Base Temp. = (max. + min.) / 2 - Base temp. If answer is negative, assume 0. Example: Calculate DD Base 50 given 65 degrees max. and 40 degrees min. Avg. = (65 + 40) / 2 = 52.5 degrees DD base 50 = 52.5 - 50 = 2.5 degrees. But look what happens given a maximum of 60 degrees and a minimum of 35 degrees: Avg. = (60 + 35) / 2 = 47.5 DD base 50 = 47.5 - 50 = -2.5 = 0 degrees. The maximum temperature was higher than the base of 50° , but no degree days were accumulated. A grower called about the first of June reporting only about 40% of the DD50 that we have recorded. -
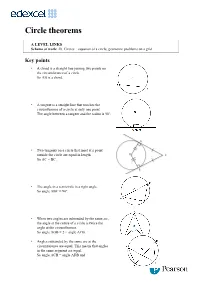
Circle Theorems
Circle theorems A LEVEL LINKS Scheme of work: 2b. Circles – equation of a circle, geometric problems on a grid Key points • A chord is a straight line joining two points on the circumference of a circle. So AB is a chord. • A tangent is a straight line that touches the circumference of a circle at only one point. The angle between a tangent and the radius is 90°. • Two tangents on a circle that meet at a point outside the circle are equal in length. So AC = BC. • The angle in a semicircle is a right angle. So angle ABC = 90°. • When two angles are subtended by the same arc, the angle at the centre of a circle is twice the angle at the circumference. So angle AOB = 2 × angle ACB. • Angles subtended by the same arc at the circumference are equal. This means that angles in the same segment are equal. So angle ACB = angle ADB and angle CAD = angle CBD. • A cyclic quadrilateral is a quadrilateral with all four vertices on the circumference of a circle. Opposite angles in a cyclic quadrilateral total 180°. So x + y = 180° and p + q = 180°. • The angle between a tangent and chord is equal to the angle in the alternate segment, this is known as the alternate segment theorem. So angle BAT = angle ACB. Examples Example 1 Work out the size of each angle marked with a letter. Give reasons for your answers. Angle a = 360° − 92° 1 The angles in a full turn total 360°. = 268° as the angles in a full turn total 360°. -

Angles ANGLE Topics • Coterminal Angles • Defintion of an Angle
Angles ANGLE Topics • Coterminal Angles • Defintion of an angle • Decimal degrees to degrees, minutes, seconds by hand using the TI-82 or TI-83 Plus • Degrees, seconds, minutes changed to decimal degree by hand using the TI-82 or TI-83 Plus • Standard position of an angle • Positive and Negative angles ___________________________________________________________________________ Definition: Angle An angle is created when a half-ray (the initial side of the angle) is drawn out of a single point (the vertex of the angle) and the ray is rotated around the point to another location (becoming the terminal side of the angle). An angle is created when a half-ray (initial side of angle) A: vertex point of angle is drawn out of a single point (vertex) AB: Initial side of angle. and the ray is rotated around the point to AC: Terminal side of angle another location (becoming the terminal side of the angle). Hence angle A is created (also called angle BAC) STANDARD POSITION An angle is in "standard position" when the vertex is at the origin and the initial side of the angle is along the positive x-axis. Recall: polynomials in algebra have a standard form (all the terms have to be listed with the term having the highest exponent first). In trigonometry, there is a standard position for angles. In this way, we are all talking about the same thing and are not trying to guess if your math solution and my math solution are the same. Not standard position. Not standard position. This IS standard position. Initial side not along Initial side along negative Initial side IS along the positive x-axis. -

Guide for the Use of the International System of Units (SI)
Guide for the Use of the International System of Units (SI) m kg s cd SI mol K A NIST Special Publication 811 2008 Edition Ambler Thompson and Barry N. Taylor NIST Special Publication 811 2008 Edition Guide for the Use of the International System of Units (SI) Ambler Thompson Technology Services and Barry N. Taylor Physics Laboratory National Institute of Standards and Technology Gaithersburg, MD 20899 (Supersedes NIST Special Publication 811, 1995 Edition, April 1995) March 2008 U.S. Department of Commerce Carlos M. Gutierrez, Secretary National Institute of Standards and Technology James M. Turner, Acting Director National Institute of Standards and Technology Special Publication 811, 2008 Edition (Supersedes NIST Special Publication 811, April 1995 Edition) Natl. Inst. Stand. Technol. Spec. Publ. 811, 2008 Ed., 85 pages (March 2008; 2nd printing November 2008) CODEN: NSPUE3 Note on 2nd printing: This 2nd printing dated November 2008 of NIST SP811 corrects a number of minor typographical errors present in the 1st printing dated March 2008. Guide for the Use of the International System of Units (SI) Preface The International System of Units, universally abbreviated SI (from the French Le Système International d’Unités), is the modern metric system of measurement. Long the dominant measurement system used in science, the SI is becoming the dominant measurement system used in international commerce. The Omnibus Trade and Competitiveness Act of August 1988 [Public Law (PL) 100-418] changed the name of the National Bureau of Standards (NBS) to the National Institute of Standards and Technology (NIST) and gave to NIST the added task of helping U.S. -

Calculus Terminology
AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential -

Applications of Geometry and Trigonometry
P1: FXS/ABE P2: FXS 9780521740517c14.xml CUAU031-EVANS September 6, 2008 13:36 CHAPTER 14 MODULE 2 Applications of geometry and trigonometry How do we apply trigonometric techniques to problems involving angles of depression and elevation? How do we apply trigonometric techniques to problems involving bearings? How do we apply trigonometric techniques to three-dimensional problems? How do we draw and interpret contour maps? How do we draw and interpret scale drawings? 14.1 Angles of elevation and depression, bearings, and triangulation Angles of elevation and depression The angle of elevation is the angle The angle of depression is the angle between the horizontal and a between the horizontal and a direction below direction above the horizontal. the horizontal. eye level line of sight angle of depression line of sight eye level cliff angle of elevation SAMPLEboat Cambridge University Press • Uncorrected Sample pages • 978-0-521-61328-6 • 2008 © Jones, Evans, Lipson TI-Nspire & Casio ClassPad material in collaboration with Brown410 and McMenamin P1: FXS/ABE P2: FXS 9780521740517c14.xml CUAU031-EVANS September 6, 2008 13:36 Chapter 14 — Applications of geometry and trigonometry 411 Bearings The three-figure bearing (or compass bearing) is the direction measured clockwise from north. The bearing of A from O is 030◦. The bearing of C from O is 210◦. The bearing of B from O is 120◦. The bearing of D from O is 330◦. N D N A 30° 330° E 120° E W O 210° W O B C S S Example 1 Angle of depression The pilot of a helicopter flying at 400 m observes a small boat at an angle of depression of 1.2◦. -

1. What Is the Radian Measure of an Angle Whose Degree Measure Is 72◦ 180◦ 72◦ = Πradians Xradians Solving for X 72Π X = Radians 180 2Π X = Radians 5 Answer: B
1. What is the radian measure of an angle whose degree measure is 72◦ 180◦ 72◦ = πradians xradians Solving for x 72π x = radians 180 2π x = radians 5 Answer: B 2. What is the length of AC? Using Pythagorean Theorem: 162 + b2 = 202 256 + b2 = 400 b2 = 144 b = 12 Answer: E 3. one solution to z2 + 64 = 0 is z2 + 64 = 0 z2 = −64 p p z2 = −64 Since there is a negative under the radical, we get imaginary roots. Thus z = −8i or z = +8i Answer: A 4. Simplifying: p 36x10y12 − 36y12 = p36y12 (x10 − 1) p = 36y12p(x10 − 1) p = 6y6 x10 − 1 Answer: C 1 5. Simplifying: 1 1 1 1 1 −3 9 6 3 −3 9 6 27a b c = 27 3 a 3 b 3 c 3 = 3a−1b3c2 3b3c2 = a Answer: C 6. Solving for x: p 8 + x + 14 = 12 p x + 14 = 12 − 8 p x + 14 = 4 p 2 x + 14 = 42 x + 14 = 16 x = 16 − 14 x = 2 Answer: C 7. Simplify x2 − 9 (x + 1)2 2x − 6 × ÷ x2 − 1 (2x + 3)(x + 3) 1 − x Rewrite as a multiplication. x2 − 9 (x + 1)2 1 − x × x2 − 1 (2x + 3)(x + 3) 2x − 6 Simplify each polynomial (x − 3)(x + 3) (x + 1)(x + 1) 1 − x × (x − 1)(x + 1) (2x + 3)(x + 3) 2(x − 3) Canceling like terms (x + 1) − 2(2x + 3) Answer: C 2 8. Simplifying: 1 11 x−5 11 + 2 2 + 2 x−5 (x−5) = (x−5) (x−5) x + 1 x + 1 x−5+11 2 = (x−5) x + 1 x+6 2 = (x−5) x + 1 x + 6 = (x − 5)2(x + 1) Answer: B 9. -

4.1 – Radian and Degree Measure
4.1 { Radian and Degree Measure Accelerated Pre-Calculus Mr. Niedert Accelerated Pre-Calculus 4.1 { Radian and Degree Measure Mr. Niedert 1 / 27 2 Radian Measure 3 Degree Measure 4 Applications 4.1 { Radian and Degree Measure 1 Angles Accelerated Pre-Calculus 4.1 { Radian and Degree Measure Mr. Niedert 2 / 27 3 Degree Measure 4 Applications 4.1 { Radian and Degree Measure 1 Angles 2 Radian Measure Accelerated Pre-Calculus 4.1 { Radian and Degree Measure Mr. Niedert 2 / 27 4 Applications 4.1 { Radian and Degree Measure 1 Angles 2 Radian Measure 3 Degree Measure Accelerated Pre-Calculus 4.1 { Radian and Degree Measure Mr. Niedert 2 / 27 4.1 { Radian and Degree Measure 1 Angles 2 Radian Measure 3 Degree Measure 4 Applications Accelerated Pre-Calculus 4.1 { Radian and Degree Measure Mr. Niedert 2 / 27 The starting position of the ray is the initial side of the angle. The position after the rotation is the terminal side of the angle. The vertex of the angle is the endpoint of the ray. Angles An angle is determine by rotating a ray about it endpoint. Accelerated Pre-Calculus 4.1 { Radian and Degree Measure Mr. Niedert 3 / 27 The position after the rotation is the terminal side of the angle. The vertex of the angle is the endpoint of the ray. Angles An angle is determine by rotating a ray about it endpoint. The starting position of the ray is the initial side of the angle. Accelerated Pre-Calculus 4.1 { Radian and Degree Measure Mr. Niedert 3 / 27 The vertex of the angle is the endpoint of the ray. -

Relationships of the SI Derived Units with Special Names and Symbols and the SI Base Units
Relationships of the SI derived units with special names and symbols and the SI base units Derived units SI BASE UNITS without special SI DERIVED UNITS WITH SPECIAL NAMES AND SYMBOLS names Solid lines indicate multiplication, broken lines indicate division kilogram kg newton (kg·m/s2) pascal (N/m2) gray (J/kg) sievert (J/kg) 3 N Pa Gy Sv MASS m FORCE PRESSURE, ABSORBED DOSE VOLUME STRESS DOSE EQUIVALENT meter m 2 m joule (N·m) watt (J/s) becquerel (1/s) hertz (1/s) LENGTH J W Bq Hz AREA ENERGY, WORK, POWER, ACTIVITY FREQUENCY second QUANTITY OF HEAT HEAT FLOW RATE (OF A RADIONUCLIDE) s m/s TIME VELOCITY katal (mol/s) weber (V·s) henry (Wb/A) tesla (Wb/m2) kat Wb H T 2 mole m/s CATALYTIC MAGNETIC INDUCTANCE MAGNETIC mol ACTIVITY FLUX FLUX DENSITY ACCELERATION AMOUNT OF SUBSTANCE coulomb (A·s) volt (W/A) C V ampere A ELECTRIC POTENTIAL, CHARGE ELECTROMOTIVE ELECTRIC CURRENT FORCE degree (K) farad (C/V) ohm (V/A) siemens (1/W) kelvin Celsius °C F W S K CELSIUS CAPACITANCE RESISTANCE CONDUCTANCE THERMODYNAMIC TEMPERATURE TEMPERATURE t/°C = T /K – 273.15 candela 2 steradian radian cd lux (lm/m ) lumen (cd·sr) 2 2 (m/m = 1) lx lm sr (m /m = 1) rad LUMINOUS INTENSITY ILLUMINANCE LUMINOUS SOLID ANGLE PLANE ANGLE FLUX The diagram above shows graphically how the 22 SI derived units with special names and symbols are related to the seven SI base units. In the first column, the symbols of the SI base units are shown in rectangles, with the name of the unit shown toward the upper left of the rectangle and the name of the associated base quantity shown in italic type below the rectangle. -

The International System of Units (SI)
NAT'L INST. OF STAND & TECH NIST National Institute of Standards and Technology Technology Administration, U.S. Department of Commerce NIST Special Publication 330 2001 Edition The International System of Units (SI) 4. Barry N. Taylor, Editor r A o o L57 330 2oOI rhe National Institute of Standards and Technology was established in 1988 by Congress to "assist industry in the development of technology . needed to improve product quality, to modernize manufacturing processes, to ensure product reliability . and to facilitate rapid commercialization ... of products based on new scientific discoveries." NIST, originally founded as the National Bureau of Standards in 1901, works to strengthen U.S. industry's competitiveness; advance science and engineering; and improve public health, safety, and the environment. One of the agency's basic functions is to develop, maintain, and retain custody of the national standards of measurement, and provide the means and methods for comparing standards used in science, engineering, manufacturing, commerce, industry, and education with the standards adopted or recognized by the Federal Government. As an agency of the U.S. Commerce Department's Technology Administration, NIST conducts basic and applied research in the physical sciences and engineering, and develops measurement techniques, test methods, standards, and related services. The Institute does generic and precompetitive work on new and advanced technologies. NIST's research facilities are located at Gaithersburg, MD 20899, and at Boulder, CO 80303. -

Classify Each Triangle by Its Side Lengths and Angle Measurements
GRADE 4 | MODULE 4 | TOPIC D | LESSONS 12–16 KEY CONCEPT OVERVIEW In Lessons 12 through 16, students explore lines of symmetry and characteristics of triangles and quadrilaterals. You can expect to see homework that asks your child to do the following: ▪ Find and draw lines of symmetry. ▪ Given half of a figure and the line of symmetry, draw the other half of the figure. ▪ Classify triangles by side lengths (e.g., equilateral, isosceles, scalene) and by angle measurements (e.g., acute, right, obtuse). ▪ Draw triangles that fit different classifications (e.g., acute and scalene). ▪ Name quadrilaterals, identify attributes (i.e., characteristics) that define them, and construct them based on given attributes. SAMPLE PROBLEM (From Lesson 13) Classify each triangle by its side lengths and angle measurements. Circle the correct names. Additional sample problems with detailed answer steps are found in the Eureka Math Homework Helpers books. Learn more at GreatMinds.org. For more resources, visit » Eureka.support GRADE 4 | MODULE 4 | TOPIC D | LESSONS 12–16 HOW YOU CAN HELP AT HOME ▪ Ask your child to look around the house for objects that have lines of symmetry. Examples include the headboard of a bed, dressers, chairs, couches, and place mats. Ask him to show where the line of symmetry would be and what makes it a line of symmetry. Be careful of objects such as doors and windows. They could have a line of symmetry, but if there’s a knob or crank on just one side, then they are not symmetrical. ▪ Ask your child to name and draw all the quadrilaterals she can think of (e.g., square, rectangle, parallelogram, trapezoid, and rhombus). -
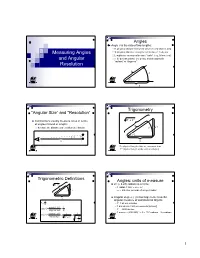
Measuring Angles and Angular Resolution
Angles Angle θ is the ratio of two lengths: R: physical distance between observer and objects [km] Measuring Angles S: physical distance along the arc between 2 objects Lengths are measured in same “units” (e.g., kilometers) and Angular θ is “dimensionless” (no units), and measured in “radians” or “degrees” Resolution R S θ R Trigonometry “Angular Size” and “Resolution” 22 Astronomers usually measure sizes in terms R +Y of angles instead of lengths R because the distances are seldom well known S Y θ θ S R R S = physical length of the arc, measured in m Y = physical length of the vertical side [m] Trigonometric Definitions Angles: units of measure R22+Y 2π (≈ 6.28) radians in a circle R 1 radian = 360˚ ÷ 2π≈57 ˚ S Y ⇒≈206,265 seconds of arc per radian θ Angular degree (˚) is too large to be a useful R S angular measure of astronomical objects θ ≡ R 1º = 60 arc minutes opposite side Y 1 arc minute = 60 arc seconds [arcsec] tan[]θ ≡= adjacent side R 1º = 3600 arcsec -1 -6 opposite sideY 1 1 arcsec ≈ (206,265) ≈ 5 × 10 radians = 5 µradians sin[]θ ≡== hypotenuse RY22+ R 2 1+ Y 2 1 Number of Degrees per Radian Trigonometry in Astronomy Y 2π radians per circle θ S R 360° Usually R >> S (particularly in astronomy), so Y ≈ S 1 radian = ≈ 57.296° 2π SY Y 1 θ ≡≈≈ ≈ ≈ 57° 17'45" RR RY22+ R 2 1+ Y 2 θ ≈≈tan[θθ] sin[ ] Relationship of Trigonometric sin[θ ] ≈ tan[θ ] ≈ θ for θ ≈ 0 Functions for Small Angles 1 sin(πx) Check it! tan(πx) 0.5 18˚ = 18˚ × (2π radians per circle) ÷ (360˚ per πx circle) = 0.1π radians ≈ 0.314 radians 0 Calculated Results