DOCSLIB.ORG

Trigonometric Functions (Memorandum № 3)

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Trigonometric Functions (Memorandum № 3) M.Eng. René Schwarz Master of Engineering in Computer Science and Communication Systems (M.Eng.) Bachelor of Engineering in Mechatronics, Industrial and Physics Technology (B.Eng.) Memorandum № 3 Trigonometric Functions Note: All angles in this paper are given in radians, unless otherwise stated. 1 Trigonometric functions and their definitions . Other (Image Credit: [3]) Function Abbreviation Geometric Description Identities ( ) opposite a π https://creativecommons.org/licenses/by-nc/4.0/ − Sine sin(α) sin α = hypothenuse = c sin α = cos α 2 ), unless otherwise stated. ( ) (α) α = adjacent = b α = α + π Cosine cos cos hypothenuse c cos sin 2 ( ) (α) α = opposite = a α = sin α = π − α = 1 Tangent tan tan adjacent b tan cos α cot ( 2 ) cot α (α) α = adjacent = b α = cos α = π − α = 1 Cotangent cot cot opposite a cot sin α( tan) 2 tan α (α) α = hypothenuse = c α = π − α = 1 Secant sec sec adjacent b sec csc ( 2 ) cos α rene-schwarz.com ( hypothenuse c π − 1 Cosecant csc(α) csc α = opposite = a csc α = sec 2 α = sin α René Schwarz 2 Shorthands Name Shorthand Name Shorthand This document is subjectLicense to (CC the conditions BY-NC 4.0), whichof the can Creative be Commons Attribution-NonCommercial examined at 4.0 International ©2017 M.Eng. licenses may apply for particular contents or supplemental documents/files. − half coversed sine (hacoversine) hacoversin α = 1 sin α versed sine (versine) versin α = 2 sin2 α = 1 − cos α 2 2 half coversed cosine (hacovercosine) hacovercosin α = 1+sin α versed cosine (vercosine) vercosin α = 2 cos2 α = 1 + cos α 2 2 exterior secant (exsecant) exsec α = sec α − 1 coversed sine (coversine) coversin α = 1 − sin α exterior cosecant (excosecant) excsc α = csc α − 1 coversed cosine (covercosine) covercosin α = 1 + sin α α 1−cos α chord crd α = 2 sin 2 half versed sine (haversine) haversin α = 2 sin(πα) cbn 1−sin α sinus cardinalis (cardinal sine) sinc α = πα (normalized) half versed cosine (havercosine) havercosin α = 2 sin α sinc α = α (unnormalized) 3 Important values of the basic trigonometric functions 1 1 1 1 2 3 5 7 5 4 3 5 7 11 0 6 π 4 π 3 π 2 π 3 π 4 π 6 π π 6 π 4 π 3 π 2 π 3 π 4 π 6 π 2π 0◦ 30◦ 45◦ 60◦ 90◦ 120◦ 135◦ 150◦ 180◦ 210◦ 225◦ 240◦ 270◦ 300◦ 315◦ 330◦ 360◦ p p p p p p p p sin α 0 1 2 3 1 3 2 1 0 − 1 − 2 − 3 −1 − 3 − 2 − 1 0 p2 p2 2 2 2p 2p p2 p2 2 2 p2 p2 cos α 1 3 2 1 0 − 1 − 2 − 3 −1 − 3 − 2 − 1 0 1 2 3 1 p2 2 p2 p2 2 p2 p2 2 p2 p2 2 2p tan α 0 3 1 3 ∞ − 3 −1 − 3 0 3 1 3 ∞ − 3 −1 − 3 0 p3 p p p3 p3 p p p3 ∞ 3 − 3 − − ∞ 3 − 3 − − ∞ cot α 3 1 3 0 3 1 3 3 1 3 0 3 1 3 Mnemonics for sine and cosine: 1 1 1 1 2 3 5 7 5 4 3 5 7 11 https://goo.gl/XB85LZ 0 6 π 4 π 3 π 2 π 3 π 4 π 6 π π 6 π 4 π 3 π 2 π 3 π 4 π 6 π 2π Errors, comments or ideas regarding! this paper? 0◦ 30◦ 45◦ 60◦ 90◦ 120◦ 135◦ 150◦ 180◦ 210◦ 225◦ 240◦ 270◦ 300◦ 315◦ 330◦ 360◦ p p p p p p p p p p p p p p p p p sin α 0 1 2 3 4 3 2 1 0 − 1 − 2 − 3 − 4 − 3 − 2 − 1 0 p2 p2 p2 p2 p2 2p 2p 2p 2p p2 p2 p2 p2 p2 p2 p2 p2 4 3 2 1 0 − 1 − 2 − 3 − 4 − 3 − 2 − 1 0 1 2 3 4 cos α 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 (Image Credit: [4]) Page 1 of 4 version: 2017/10/05 14:56 M.Eng. René Schwarz (rene-schwarz.com): Memorandum Series Trigonometric Functions (Memorandum № 3) 4 Pythagorean and related trigonometric identities cos2 α + sin2 α = 1 in terms of sin α cos α tan α cot α sec α csc α p (Pythagorean Identity, p tan α 1 sec2 α − 1 1 sin α = sin α 1 − cos2 α p p named after 1 + tan2 α 1 + cot2 α sec α p csc α Pythagoras of Samos p 1 cot α 1 csc2 α − 1 cos α = 1 − sin2 α cos α p p Ὁ Πυθαγόρας ὁ Σάμιος) 2 2 p 1 + tan α 1 + cot α sec α csc α sin α 1 − cos2 α 1 p 1 2 1 tan α = p tan α sec2 α − 1 p 1 + tan α = − 2 α α 2 − cos2 α p1 sin α cos cot csc α 1 1 − sin2 α cos α 1 1 p = sec2 α cot α = p cot α p csc2 α − 1 sin α 1 − cos2 α tan α p sec2 α − 1 1 1 1 p 1 + cot2 α csc α 1 + cot2 α = sec α = p 1 + tan2 α sec α p sin2 α 1 − sin2 α cos α p cot α csc2 α − 1 p 2 1 1 1 + tan2 α sec α = csc α csc α = p 1 + cot2 α p csc α sin α 1 − cos2 α tan α sec2 α − 1 5 Symmetry, shifts and periodicity Symmetry Shifts Periodicity (k 2 Z) − − π − − π · sin( α) = sin α x = 2 α π α α + 2 α + π α + 2π sin(α + k 2π) = sin α − cos(−α) = cos α sin x = cos α sin α cos α sin α sin α cos(α + k · 2π) = cos α cos x = sin α − cos α − sin α − cos α cos α tan(−α) = − tan α tan(α + k · π) = tan α tan x = cot α − tan α − cot α tan α tan α (−α) = − α · cot cot cot x = tan α − cot α − tan α cot α cot α cot(α + k π) = cot α sec(−α) = sec α sec x = csc α − sec α − csc α − sec α sec α sec(α + k · 2π) = sec α csc(−α) = − csc α csc x = sec α csc α sec α − csc α csc α csc(α + k · 2π) = csc α 6 Addition theorems, sum and difference identities of two functions α+β α−β sin(αβ) sin(α β) = sin α cos β cos α sin β sin α + sin β = 2 sin 2 cos 2 tan α tan β = cos α cos β ∓ − α+β α−β sin(αβ) cos(α β) = cos α cos β sin α sin β sin α sin β = 2 cos 2 sin 2 cot α cot β = sin α sin β tan αtan β α+β α−β cos(α−β) tan(α β) = 1∓tan α tan β cos α + cos β = 2 cos 2 cos 2 tan α + cot β = cos α sin β cot α cot β∓1 − − α+β α−β − cos(α+β) cot(α β) = cot βcot α cos α sin β = 2 sin 2 sin 2 cot α tan β = sin α cos β 7 Products of two functions 1 − − 1 − sin α sin β = 2 (cos(α β) cos(α + β)) sin α cos β = 2 (sin(α β) + sin(α + β)) 1 − − 1 − cos α sin β = 2 (sin(α β) sin(α + β)) cos α cos β = 2 (cos(α β) + cos(α + β)) 8 Power reduction formula Sine Cosine n−1 ( ) n−1 X2 − ( ) X2 ( ) 2 n 1 −k n 2 n n odd sinn α = (−1) 2 sin ((n − 2k)α) cosn α = cos ((n − 2k)α) 2n k 2n k k=0 k=0 n −1 n −1 ( ) 2X ( ) ( ) 2X ( ) n 1 n 2 n −k n n 1 n 2 n n even sin α = + (−1)( 2 ) cos ((n − 2k)α) cos α = + cos ((n − 2k)α) 2n n 2n k 2n n 2n k 2 k=0 2 k=0 1 − cos(2α) 3 sin α − sin(3α) cos(4α) − 4 cos(2α) + 3 sin2 α = sin3 α = sin4 α = 2 4 8 1 + cos(2α) cos(3α) + 3 cos α cos(4α) + 4 cos(2α) + 3 cos2 α = cos3 α = cos4 α = 2 4 8 Page 2 of 4 version: 2017/10/05 14:56 M.Eng. René Schwarz (rene-schwarz.com): Memorandum Series Trigonometric Functions (Memorandum № 3) 9 Multiple-angle formulæ Pn ( ) n k n−k π(n−k) tan(nθ)+tan θ sin(nθ) = k cos θ sin θ sin 2 tan((n + 1)θ) = 1−tan(nθ) tan θ k=0 Pn ( ) n k n−k π(n−k) cot(nθ) cot θ−1 cos(nθ) = k cos θ sin θ cos 2 cot((n + 1)θ) = cot(nθ)+cot θ k=0 sin x cos x tan x cot x 2 tan α 2 − 2 1−tan2 α 2 tan α cot2 α−1 x = 2α 2 sin α cos α = 1+tan2 α cos α sin α = 1+tan2 α 1−tan2 α 2 cot α − 3 3 − 3 tan α−tan3 α cot3 α−3 cot α x = 3α 3 sin α 4 sin α 4 cos α 3 cos α 1−3 tan2 α 3 cot2 α−1 3 − 4 − 2 4 tan α−4 tan3 α cot4 α−6 cot2 α+1 x = 4α 8 cos α sin α 4 cos α sin α 8 cos α 8 cos α + 1 1−6 tan2 α+tan4 α 4 cot3 α−4 cot α 10 Half-angle formulæ q q α 1 − α 1−cos α 1−cos α sin α − sin 2 = 2 (1 cos α) tan 2 = 1+cos α = sin α = 1+cos α = csc α cot α q q α 1 α 1+cos α 1+cos α sin α cos 2 = 2 (1 + cos α) cot 2 = 1−cos α = sin α = 1−cos α = csc α + cot α 11 Inverse trigonometric functions 11.1 Definition of the inverse trigonometric functions Trig.
Load more

Recommended publications
  • Refresher Course Content
    Calculus I Refresher Course Content 4. Exponential and Logarithmic Functions Section 4.1: Exponential Functions Section 4.2: Logarithmic Functions Section 4.3: Properties of Logarithms Section 4.4: Exponential and Logarithmic Equations Section 4.5: Exponential Growth and Decay; Modeling Data 5. Trigonometric Functions Section 5.1: Angles and Radian Measure Section 5.2: Right Triangle Trigonometry Section 5.3: Trigonometric Functions of Any Angle Section 5.4: Trigonometric Functions of Real Numbers; Periodic Functions Section 5.5: Graphs of Sine and Cosine Functions Section 5.6: Graphs of Other Trigonometric Functions Section 5.7: Inverse Trigonometric Functions Section 5.8: Applications of Trigonometric Functions 6. Analytic Trigonometry Section 6.1: Verifying Trigonometric Identities Section 6.2: Sum and Difference Formulas Section 6.3: Double-Angle, Power-Reducing, and Half-Angle Formulas Section 6.4: Product-to-Sum and Sum-to-Product Formulas Section 6.5: Trigonometric Equations 7. Additional Topics in Trigonometry Section 7.1: The Law of Sines Section 7.2: The Law of Cosines Section 7.3: Polar Coordinates Section 7.4: Graphs of Polar Equations Section 7.5: Complex Numbers in Polar Form; DeMoivre’s Theorem Section 7.6: Vectors Section 7.7: The Dot Product 8. Systems of Equations and Inequalities (partially included) Section 8.1: Systems of Linear Equations in Two Variables Section 8.2: Systems of Linear Equations in Three Variables Section 8.3: Partial Fractions Section 8.4: Systems of Nonlinear Equations in Two Variables Section 8.5: Systems of Inequalities Section 8.6: Linear Programming 10. Conic Sections and Analytic Geometry (partially included) Section 10.1: The Ellipse Section 10.2: The Hyperbola Section 10.3: The Parabola Section 10.4: Rotation of Axes Section 10.5: Parametric Equations Section 10.6: Conic Sections in Polar Coordinates 11.
    [Show full text]
  • Trigonometric Functions
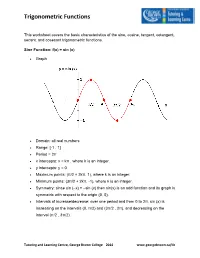
    Trigonometric Functions This worksheet covers the basic characteristics of the sine, cosine, tangent, cotangent, secant, and cosecant trigonometric functions. Sine Function: f(x) = sin (x) • Graph • Domain: all real numbers • Range: [-1 , 1] • Period = 2π • x intercepts: x = kπ , where k is an integer. • y intercepts: y = 0 • Maximum points: (π/2 + 2kπ, 1), where k is an integer. • Minimum points: (3π/2 + 2kπ, -1), where k is an integer. • Symmetry: since sin (–x) = –sin (x) then sin(x) is an odd function and its graph is symmetric with respect to the origin (0, 0). • Intervals of increase/decrease: over one period and from 0 to 2π, sin (x) is increasing on the intervals (0, π/2) and (3π/2 , 2π), and decreasing on the interval (π/2 , 3π/2). Tutoring and Learning Centre, George Brown College 2014 www.georgebrown.ca/tlc Trigonometric Functions Cosine Function: f(x) = cos (x) • Graph • Domain: all real numbers • Range: [–1 , 1] • Period = 2π • x intercepts: x = π/2 + k π , where k is an integer. • y intercepts: y = 1 • Maximum points: (2 k π , 1) , where k is an integer. • Minimum points: (π + 2 k π , –1) , where k is an integer. • Symmetry: since cos(–x) = cos(x) then cos (x) is an even function and its graph is symmetric with respect to the y axis. • Intervals of increase/decrease: over one period and from 0 to 2π, cos (x) is decreasing on (0 , π) increasing on (π , 2π). Tutoring and Learning Centre, George Brown College 2014 www.georgebrown.ca/tlc Trigonometric Functions Tangent Function : f(x) = tan (x) • Graph • Domain: all real numbers except π/2 + k π, k is an integer.
    [Show full text]
  • Lecture 5: Complex Logarithm and Trigonometric Functions
    LECTURE 5: COMPLEX LOGARITHM AND TRIGONOMETRIC FUNCTIONS Let C∗ = C \{0}. Recall that exp : C → C∗ is surjective (onto), that is, given w ∈ C∗ with w = ρ(cos φ + i sin φ), ρ = |w|, φ = Arg w we have ez = w where z = ln ρ + iφ (ln stands for the real log) Since exponential is not injective (one one) it does not make sense to talk about the inverse of this function. However, we also know that exp : H → C∗ is bijective. So, what is the inverse of this function? Well, that is the logarithm. We start with a general definition Definition 1. For z ∈ C∗ we define log z = ln |z| + i argz. Here ln |z| stands for the real logarithm of |z|. Since argz = Argz + 2kπ, k ∈ Z it follows that log z is not well defined as a function (it is multivalued), which is something we find difficult to handle. It is time for another definition. Definition 2. For z ∈ C∗ the principal value of the logarithm is defined as Log z = ln |z| + i Argz. Thus the connection between the two definitions is Log z + 2kπ = log z for some k ∈ Z. Also note that Log : C∗ → H is well defined (now it is single valued). Remark: We have the following observations to make, (1) If z 6= 0 then eLog z = eln |z|+i Argz = z (What about Log (ez)?). (2) Suppose x is a positive real number then Log x = ln x + i Argx = ln x (for positive real numbers we do not get anything new).
    [Show full text]
  • Unit Circle Trigonometry
    UNIT CIRCLE TRIGONOMETRY The Unit Circle is the circle centered at the origin with radius 1 unit (hence, the “unit” circle). The equation of this circle is xy22+ =1. A diagram of the unit circle is shown below: y xy22+ = 1 1 x -2 -1 1 2 -1 -2 We have previously applied trigonometry to triangles that were drawn with no reference to any coordinate system. Because the radius of the unit circle is 1, we will see that it provides a convenient framework within which we can apply trigonometry to the coordinate plane. Drawing Angles in Standard Position We will first learn how angles are drawn within the coordinate plane. An angle is said to be in standard position if the vertex of the angle is at (0, 0) and the initial side of the angle lies along the positive x-axis. If the angle measure is positive, then the angle has been created by a counterclockwise rotation from the initial to the terminal side. If the angle measure is negative, then the angle has been created by a clockwise rotation from the initial to the terminal side. θ in standard position, where θ is positive: θ in standard position, where θ is negative: y y Terminal side θ Initial side x x Initial side θ Terminal side Unit Circle Trigonometry Drawing Angles in Standard Position Examples The following angles are drawn in standard position: y y 1. θ = 40D 2. θ =160D θ θ x x y 3. θ =−320D Notice that the terminal sides in examples 1 and 3 are in the same position, but they do not represent the same angle (because x the amount and direction of the rotation θ in each is different).
    [Show full text]
  • Construction Surveying Curves
    Construction Surveying Curves Three(3) Continuing Education Hours Course #LS1003 Approved Continuing Education for Licensed Professional Engineers EZ-pdh.com Ezekiel Enterprises, LLC 301 Mission Dr. Unit 571 New Smyrna Beach, FL 32170 800-433-1487 [email protected] Construction Surveying Curves Ezekiel Enterprises, LLC Course Description: The Construction Surveying Curves course satisfies three (3) hours of professional development. The course is designed as a distance learning course focused on the process required for a surveyor to establish curves. Objectives: The primary objective of this course is enable the student to understand practical methods to locate points along curves using variety of methods. Grading: Students must achieve a minimum score of 70% on the online quiz to pass this course. The quiz may be taken as many times as necessary to successful pass and complete the course. Ezekiel Enterprises, LLC Section I. Simple Horizontal Curves CURVE POINTS Simple The simple curve is an arc of a circle. It is the most By studying this course the surveyor learns to locate commonly used. The radius of the circle determines points using angles and distances. In construction the “sharpness” or “flatness” of the curve. The larger surveying, the surveyor must often establish the line of the radius, the “flatter” the curve. a curve for road layout or some other construction. The surveyor can establish curves of short radius, Compound usually less than one tape length, by holding one end Surveyors often have to use a compound curve because of the tape at the center of the circle and swinging the of the terrain.
    [Show full text]
  • Lesson 6: Trigonometric Identities
    1. Introduction An identity is an equality relationship between two mathematical expressions. For example, in basic algebra students are expected to master various algbriac factoring identities such as a2 − b2 =(a − b)(a + b)or a3 + b3 =(a + b)(a2 − ab + b2): Identities such as these are used to simplifly algebriac expressions and to solve alge- a3 + b3 briac equations. For example, using the third identity above, the expression a + b simpliflies to a2 − ab + b2: The first identiy verifies that the equation (a2 − b2)=0is true precisely when a = b: The formulas or trigonometric identities introduced in this lesson constitute an integral part of the study and applications of trigonometry. Such identities can be used to simplifly complicated trigonometric expressions. This lesson contains several examples and exercises to demonstrate this type of procedure. Trigonometric identities can also used solve trigonometric equations. Equations of this type are introduced in this lesson and examined in more detail in Lesson 7. For student’s convenience, the identities presented in this lesson are sumarized in Appendix A 2. The Elementary Identities Let (x; y) be the point on the unit circle centered at (0; 0) that determines the angle t rad : Recall that the definitions of the trigonometric functions for this angle are sin t = y tan t = y sec t = 1 x y : cos t = x cot t = x csc t = 1 y x These definitions readily establish the first of the elementary or fundamental identities given in the table below. For obvious reasons these are often referred to as the reciprocal and quotient identities.
    [Show full text]
  • And Are Congruent Chords, So the Corresponding Arcs RS and ST Are Congruent
    9-3 Arcs and Chords ALGEBRA Find the value of x. 3. SOLUTION: 1. In the same circle or in congruent circles, two minor SOLUTION: arcs are congruent if and only if their corresponding Arc ST is a minor arc, so m(arc ST) is equal to the chords are congruent. Since m(arc AB) = m(arc CD) measure of its related central angle or 93. = 127, arc AB arc CD and . and are congruent chords, so the corresponding arcs RS and ST are congruent. m(arc RS) = m(arc ST) and by substitution, x = 93. ANSWER: 93 ANSWER: 3 In , JK = 10 and . Find each measure. Round to the nearest hundredth. 2. SOLUTION: Since HG = 4 and FG = 4, and are 4. congruent chords and the corresponding arcs HG and FG are congruent. SOLUTION: m(arc HG) = m(arc FG) = x Radius is perpendicular to chord . So, by Arc HG, arc GF, and arc FH are adjacent arcs that Theorem 10.3, bisects arc JKL. Therefore, m(arc form the circle, so the sum of their measures is 360. JL) = m(arc LK). By substitution, m(arc JL) = or 67. ANSWER: 67 ANSWER: 70 eSolutions Manual - Powered by Cognero Page 1 9-3 Arcs and Chords 5. PQ ALGEBRA Find the value of x. SOLUTION: Draw radius and create right triangle PJQ. PM = 6 and since all radii of a circle are congruent, PJ = 6. Since the radius is perpendicular to , bisects by Theorem 10.3. So, JQ = (10) or 5. 7. Use the Pythagorean Theorem to find PQ.
    [Show full text]
  • Trigonometry and Spherical Astronomy 1. Sines and Chords
    CHAPTER TWO TRIGONOMETRY AND SPHERICAL ASTRONOMY 1. Sines and Chords In Almagest I.11 Ptolemy displayed a table of chords, the construction of which is explained in the previous chapter. The chord of a central angle α in a circle is the segment subtended by that angle α. If the radius of the circle (the “norm” of the table) is taken as 60 units, the chord can be expressed by means of the modern sine function: crd α = 120 · sin (α/2). In Ptolemy’s table (Toomer 1984, pp. 57–60), the argument, α, is given at intervals of ½° from ½° to 180°. Columns II and III display the chord, in units, minutes, and seconds of a unit, and the increase, in the same units, in crd α corresponding to an increase of one minute in α, computed by taking 1/30 of the difference between successive entries in column II (Aaboe 1964, pp. 101–125). For an insightful account on Ptolemy’s chord table, see Van Brummelen 2009, where many issues underlying the tables for trigonometry and spherical astronomy are addressed. By contrast, al-Khwārizmī’s zij originally had a table of sines for integer degrees with a norm of 150 (Neugebauer 1962a, p. 104) that has uniquely survived in manuscripts associated with the Toledan Tables (Toomer 1968, p. 27; F. S. Pedersen 2002, pp. 946–952). The corresponding table in al-Battānī’s zij displays the sine of the argu- ment at intervals of ½° with a norm of 60 (Nallino 1903–1907, 2:55– 56). This table is reproduced, essentially unchanged, in the Toledan Tables (Toomer 1968, p.
    [Show full text]
  • Notes on Curves for Railways
    NOTES ON CURVES FOR RAILWAYS BY V B SOOD PROFESSOR BRIDGES INDIAN RAILWAYS INSTITUTE OF CIVIL ENGINEERING PUNE- 411001 Notes on —Curves“ Dated 040809 1 COMMONLY USED TERMS IN THE BOOK BG Broad Gauge track, 1676 mm gauge MG Meter Gauge track, 1000 mm gauge NG Narrow Gauge track, 762 mm or 610 mm gauge G Dynamic Gauge or center to center of the running rails, 1750 mm for BG and 1080 mm for MG g Acceleration due to gravity, 9.81 m/sec2 KMPH Speed in Kilometers Per Hour m/sec Speed in metres per second m/sec2 Acceleration in metre per second square m Length or distance in metres cm Length or distance in centimetres mm Length or distance in millimetres D Degree of curve R Radius of curve Ca Actual Cant or superelevation provided Cd Cant Deficiency Cex Cant Excess Camax Maximum actual Cant or superelevation permissible Cdmax Maximum Cant Deficiency permissible Cexmax Maximum Cant Excess permissible Veq Equilibrium Speed Vg Booked speed of goods trains Vmax Maximum speed permissible on the curve BG SOD Indian Railways Schedule of Dimensions 1676 mm Gauge, Revised 2004 IR Indian Railways IRPWM Indian Railways Permanent Way Manual second reprint 2004 IRTMM Indian railways Track Machines Manual , March 2000 LWR Manual Manual of Instructions on Long Welded Rails, 1996 Notes on —Curves“ Dated 040809 2 PWI Permanent Way Inspector, Refers to Senior Section Engineer, Section Engineer or Junior Engineer looking after the Permanent Way or Track on Indian railways. The term may also include the Permanent Way Supervisor/ Gang Mate etc who might look after the maintenance work in the track.
    [Show full text]
  • 20. Geometry of the Circle (SC)
    20. GEOMETRY OF THE CIRCLE PARTS OF THE CIRCLE Segments When we speak of a circle we may be referring to the plane figure itself or the boundary of the shape, called the circumference. In solving problems involving the circle, we must be familiar with several theorems. In order to understand these theorems, we review the names given to parts of a circle. Diameter and chord The region that is encompassed between an arc and a chord is called a segment. The region between the chord and the minor arc is called the minor segment. The region between the chord and the major arc is called the major segment. If the chord is a diameter, then both segments are equal and are called semi-circles. The straight line joining any two points on the circle is called a chord. Sectors A diameter is a chord that passes through the center of the circle. It is, therefore, the longest possible chord of a circle. In the diagram, O is the center of the circle, AB is a diameter and PQ is also a chord. Arcs The region that is enclosed by any two radii and an arc is called a sector. If the region is bounded by the two radii and a minor arc, then it is called the minor sector. www.faspassmaths.comIf the region is bounded by two radii and the major arc, it is called the major sector. An arc of a circle is the part of the circumference of the circle that is cut off by a chord.
    [Show full text]
  • Calculus Terminology
    AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential
    [Show full text]
  • Trigonometric Functions
    Hy po e te t n C i u s se o b a p p O θ A c B Adjacent Math 1060 ~ Trigonometry 4 The Six Trigonometric Functions Learning Objectives In this section you will: • Determine the values of the six trigonometric functions from the coordinates of a point on the Unit Circle. • Learn and apply the reciprocal and quotient identities. • Learn and apply the Generalized Reference Angle Theorem. • Find angles that satisfy trigonometric function equations. The Trigonometric Functions In addition to the sine and cosine functions, there are four more. Trigonometric Functions: y Ex 1: Assume � is in this picture. P(cos(�), sin(�)) Find the six trigonometric functions of �. x 1 1 Ex 2: Determine the tangent values for the first quadrant and each of the quadrant angles on this Unit Circle. Reciprocal and Quotient Identities Ex 3: Find the indicated value, if it exists. a) sec 30º b) csc c) cot (2) d) tan �, where � is any angle coterminal with 270 º. e) cos �, where csc � = -2 and < � < . f) sin �, where tan � = and � is in Q III. 2 Generalized Reference Angle Theorem The values of the trigonometric functions of an angle, if they exist, are the same, up to a sign, as the corresponding trigonometric functions of the reference angle. More specifically, if α is the reference angle for θ, then cos θ = ± cos α, sin θ = ± sin α. The sign, + or –, is determined by the quadrant in which the terminal side of θ lies. Ex 4: Determine the reference angle for each of these. Then state the cosine and sine and tangent of each.
    [Show full text]