Using Differentials to Differentiate Trigonometric and Exponential Functions Tevian Dray
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Refresher Course Content
Calculus I Refresher Course Content 4. Exponential and Logarithmic Functions Section 4.1: Exponential Functions Section 4.2: Logarithmic Functions Section 4.3: Properties of Logarithms Section 4.4: Exponential and Logarithmic Equations Section 4.5: Exponential Growth and Decay; Modeling Data 5. Trigonometric Functions Section 5.1: Angles and Radian Measure Section 5.2: Right Triangle Trigonometry Section 5.3: Trigonometric Functions of Any Angle Section 5.4: Trigonometric Functions of Real Numbers; Periodic Functions Section 5.5: Graphs of Sine and Cosine Functions Section 5.6: Graphs of Other Trigonometric Functions Section 5.7: Inverse Trigonometric Functions Section 5.8: Applications of Trigonometric Functions 6. Analytic Trigonometry Section 6.1: Verifying Trigonometric Identities Section 6.2: Sum and Difference Formulas Section 6.3: Double-Angle, Power-Reducing, and Half-Angle Formulas Section 6.4: Product-to-Sum and Sum-to-Product Formulas Section 6.5: Trigonometric Equations 7. Additional Topics in Trigonometry Section 7.1: The Law of Sines Section 7.2: The Law of Cosines Section 7.3: Polar Coordinates Section 7.4: Graphs of Polar Equations Section 7.5: Complex Numbers in Polar Form; DeMoivre’s Theorem Section 7.6: Vectors Section 7.7: The Dot Product 8. Systems of Equations and Inequalities (partially included) Section 8.1: Systems of Linear Equations in Two Variables Section 8.2: Systems of Linear Equations in Three Variables Section 8.3: Partial Fractions Section 8.4: Systems of Nonlinear Equations in Two Variables Section 8.5: Systems of Inequalities Section 8.6: Linear Programming 10. Conic Sections and Analytic Geometry (partially included) Section 10.1: The Ellipse Section 10.2: The Hyperbola Section 10.3: The Parabola Section 10.4: Rotation of Axes Section 10.5: Parametric Equations Section 10.6: Conic Sections in Polar Coordinates 11. -

Trigonometric Functions
Trigonometric Functions This worksheet covers the basic characteristics of the sine, cosine, tangent, cotangent, secant, and cosecant trigonometric functions. Sine Function: f(x) = sin (x) • Graph • Domain: all real numbers • Range: [-1 , 1] • Period = 2π • x intercepts: x = kπ , where k is an integer. • y intercepts: y = 0 • Maximum points: (π/2 + 2kπ, 1), where k is an integer. • Minimum points: (3π/2 + 2kπ, -1), where k is an integer. • Symmetry: since sin (–x) = –sin (x) then sin(x) is an odd function and its graph is symmetric with respect to the origin (0, 0). • Intervals of increase/decrease: over one period and from 0 to 2π, sin (x) is increasing on the intervals (0, π/2) and (3π/2 , 2π), and decreasing on the interval (π/2 , 3π/2). Tutoring and Learning Centre, George Brown College 2014 www.georgebrown.ca/tlc Trigonometric Functions Cosine Function: f(x) = cos (x) • Graph • Domain: all real numbers • Range: [–1 , 1] • Period = 2π • x intercepts: x = π/2 + k π , where k is an integer. • y intercepts: y = 1 • Maximum points: (2 k π , 1) , where k is an integer. • Minimum points: (π + 2 k π , –1) , where k is an integer. • Symmetry: since cos(–x) = cos(x) then cos (x) is an even function and its graph is symmetric with respect to the y axis. • Intervals of increase/decrease: over one period and from 0 to 2π, cos (x) is decreasing on (0 , π) increasing on (π , 2π). Tutoring and Learning Centre, George Brown College 2014 www.georgebrown.ca/tlc Trigonometric Functions Tangent Function : f(x) = tan (x) • Graph • Domain: all real numbers except π/2 + k π, k is an integer. -

Lecture 5: Complex Logarithm and Trigonometric Functions
LECTURE 5: COMPLEX LOGARITHM AND TRIGONOMETRIC FUNCTIONS Let C∗ = C \{0}. Recall that exp : C → C∗ is surjective (onto), that is, given w ∈ C∗ with w = ρ(cos φ + i sin φ), ρ = |w|, φ = Arg w we have ez = w where z = ln ρ + iφ (ln stands for the real log) Since exponential is not injective (one one) it does not make sense to talk about the inverse of this function. However, we also know that exp : H → C∗ is bijective. So, what is the inverse of this function? Well, that is the logarithm. We start with a general definition Definition 1. For z ∈ C∗ we define log z = ln |z| + i argz. Here ln |z| stands for the real logarithm of |z|. Since argz = Argz + 2kπ, k ∈ Z it follows that log z is not well defined as a function (it is multivalued), which is something we find difficult to handle. It is time for another definition. Definition 2. For z ∈ C∗ the principal value of the logarithm is defined as Log z = ln |z| + i Argz. Thus the connection between the two definitions is Log z + 2kπ = log z for some k ∈ Z. Also note that Log : C∗ → H is well defined (now it is single valued). Remark: We have the following observations to make, (1) If z 6= 0 then eLog z = eln |z|+i Argz = z (What about Log (ez)?). (2) Suppose x is a positive real number then Log x = ln x + i Argx = ln x (for positive real numbers we do not get anything new). -

An Appreciation of Euler's Formula
Rose-Hulman Undergraduate Mathematics Journal Volume 18 Issue 1 Article 17 An Appreciation of Euler's Formula Caleb Larson North Dakota State University Follow this and additional works at: https://scholar.rose-hulman.edu/rhumj Recommended Citation Larson, Caleb (2017) "An Appreciation of Euler's Formula," Rose-Hulman Undergraduate Mathematics Journal: Vol. 18 : Iss. 1 , Article 17. Available at: https://scholar.rose-hulman.edu/rhumj/vol18/iss1/17 Rose- Hulman Undergraduate Mathematics Journal an appreciation of euler's formula Caleb Larson a Volume 18, No. 1, Spring 2017 Sponsored by Rose-Hulman Institute of Technology Department of Mathematics Terre Haute, IN 47803 [email protected] a scholar.rose-hulman.edu/rhumj North Dakota State University Rose-Hulman Undergraduate Mathematics Journal Volume 18, No. 1, Spring 2017 an appreciation of euler's formula Caleb Larson Abstract. For many mathematicians, a certain characteristic about an area of mathematics will lure him/her to study that area further. That characteristic might be an interesting conclusion, an intricate implication, or an appreciation of the impact that the area has upon mathematics. The particular area that we will be exploring is Euler's Formula, eix = cos x + i sin x, and as a result, Euler's Identity, eiπ + 1 = 0. Throughout this paper, we will develop an appreciation for Euler's Formula as it combines the seemingly unrelated exponential functions, imaginary numbers, and trigonometric functions into a single formula. To appreciate and further understand Euler's Formula, we will give attention to the individual aspects of the formula, and develop the necessary tools to prove it. -

Einstein's Velocity Addition Law and Its Hyperbolic Geometry
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector Computers and Mathematics with Applications 53 (2007) 1228–1250 www.elsevier.com/locate/camwa Einstein’s velocity addition law and its hyperbolic geometry Abraham A. Ungar∗ Department of Mathematics, North Dakota State University, Fargo, ND 58105, USA Received 6 March 2006; accepted 19 May 2006 Abstract Following a brief review of the history of the link between Einstein’s velocity addition law of special relativity and the hyperbolic geometry of Bolyai and Lobachevski, we employ the binary operation of Einstein’s velocity addition to introduce into hyperbolic geometry the concepts of vectors, angles and trigonometry. In full analogy with Euclidean geometry, we show in this article that the introduction of these concepts into hyperbolic geometry leads to hyperbolic vector spaces. The latter, in turn, form the setting for hyperbolic geometry just as vector spaces form the setting for Euclidean geometry. c 2007 Elsevier Ltd. All rights reserved. Keywords: Special relativity; Einstein’s velocity addition law; Thomas precession; Hyperbolic geometry; Hyperbolic trigonometry 1. Introduction The hyperbolic law of cosines is nearly a century old result that has sprung from the soil of Einstein’s velocity addition law that Einstein introduced in his 1905 paper [1,2] that founded the special theory of relativity. It was established by Sommerfeld (1868–1951) in 1909 [3] in terms of hyperbolic trigonometric functions as a consequence of Einstein’s velocity addition of relativistically admissible velocities. Soon after, Varicakˇ (1865–1942) established in 1912 [4] the interpretation of Sommerfeld’s consequence in the hyperbolic geometry of Bolyai and Lobachevski. -

Old-Fashioned Relativity & Relativistic Space-Time Coordinates
Relativistic Coordinates-Classic Approach 4.A.1 Appendix 4.A Relativistic Space-time Coordinates The nature of space-time coordinate transformation will be described here using a fictional spaceship traveling at half the speed of light past two lighthouses. In Fig. 4.A.1 the ship is just passing the Main Lighthouse as it blinks in response to a signal from the North lighthouse located at one light second (about 186,000 miles or EXACTLY 299,792,458 meters) above Main. (Such exactitude is the result of 1970-80 work by Ken Evenson's lab at NIST (National Institute of Standards and Technology in Boulder) and adopted by International Standards Committee in 1984.) Now the speed of light c is a constant by civil law as well as physical law! This came about because time and frequency measurement became so much more precise than distance measurement that it was decided to define the meter in terms of c. Fig. 4.A.1 Ship passing Main Lighthouse as it blinks at t=0. This arrangement is a simplified model for a 1Hz laser resonator. The two lighthouses use each other to maintain a strict one-second time period between blinks. And, strict it must be to do relativistic timing. (Even stricter than NIST is the universal agency BIGANN or Bureau of Intergalactic Aids to Navigation at Night.) The simulations shown here are done using RelativIt. Relativistic Coordinates-Classic Approach 4.A.2 Fig. 4.A.2 Main and North Lighthouses blink each other at precisely t=1. At p recisel y t=1 sec. -

Hyperbolic Trigonometry in Two-Dimensional Space-Time Geometry
Hyperbolic trigonometry in two-dimensional space-time geometry F. Catoni, R. Cannata, V. Catoni, P. Zampetti ENEA; Centro Ricerche Casaccia; Via Anguillarese, 301; 00060 S.Maria di Galeria; Roma; Italy January 22, 2003 Summary.- By analogy with complex numbers, a system of hyperbolic numbers can be intro- duced in the same way: z = x + hy; h2 = 1 x, y R . As complex numbers are linked to the { ∈ } Euclidean geometry, so this system of numbers is linked to the pseudo-Euclidean plane geometry (space-time geometry). In this paper we will show how this system of numbers allows, by means of a Cartesian representa- tion, an operative definition of hyperbolic functions using the invariance respect to special relativity Lorentz group. From this definition, by using elementary mathematics and an Euclidean approach, it is straightforward to formalise the pseudo-Euclidean trigonometry in the Cartesian plane with the same coherence as the Euclidean trigonometry. PACS 03 30 - Special Relativity PACS 02.20. Hj - Classical groups and Geometries 1 Introduction Complex numbers are strictly related to the Euclidean geometry: indeed their invariant (the module) arXiv:math-ph/0508011v1 3 Aug 2005 is the same as the Pythagoric distance (Euclidean invariant) and their unimodular multiplicative group is the Euclidean rotation group. It is well known that these properties allow to use complex numbers for representing plane vectors. In the same way hyperbolic numbers, an extension of complex numbers [1, 2] defined as z = x + hy; h2 =1 x, y R , { ∈ } are strictly related to space-time geometry [2, 3, 4]. Indeed their square module given by1 z 2 = 2 2 | | zz˜ x y is the Lorentz invariant of two dimensional special relativity, and their unimodular multiplicative≡ − group is the special relativity Lorentz group [2]. -

Hyperbolic Geometry
Flavors of Geometry MSRI Publications Volume 31,1997 Hyperbolic Geometry JAMES W. CANNON, WILLIAM J. FLOYD, RICHARD KENYON, AND WALTER R. PARRY Contents 1. Introduction 59 2. The Origins of Hyperbolic Geometry 60 3. Why Call it Hyperbolic Geometry? 63 4. Understanding the One-Dimensional Case 65 5. Generalizing to Higher Dimensions 67 6. Rudiments of Riemannian Geometry 68 7. Five Models of Hyperbolic Space 69 8. Stereographic Projection 72 9. Geodesics 77 10. Isometries and Distances in the Hyperboloid Model 80 11. The Space at Infinity 84 12. The Geometric Classification of Isometries 84 13. Curious Facts about Hyperbolic Space 86 14. The Sixth Model 95 15. Why Study Hyperbolic Geometry? 98 16. When Does a Manifold Have a Hyperbolic Structure? 103 17. How to Get Analytic Coordinates at Infinity? 106 References 108 Index 110 1. Introduction Hyperbolic geometry was created in the first half of the nineteenth century in the midst of attempts to understand Euclid’s axiomatic basis for geometry. It is one type of non-Euclidean geometry, that is, a geometry that discards one of Euclid’s axioms. Einstein and Minkowski found in non-Euclidean geometry a This work was supported in part by The Geometry Center, University of Minnesota, an STC funded by NSF, DOE, and Minnesota Technology, Inc., by the Mathematical Sciences Research Institute, and by NSF research grants. 59 60 J. W. CANNON, W. J. FLOYD, R. KENYON, AND W. R. PARRY geometric basis for the understanding of physical time and space. In the early part of the twentieth century every serious student of mathematics and physics studied non-Euclidean geometry. -
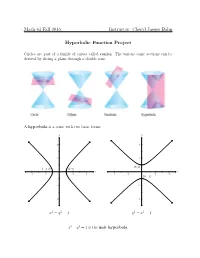
Cheryl Jaeger Balm Hyperbolic Function Project
Math 43 Fall 2016 Instructor: Cheryl Jaeger Balm Hyperbolic Function Project Circles are part of a family of curves called conics. The various conic sections can be derived by slicing a plane through a double cone. A hyperbola is a conic with two basic forms: y y 4 4 2 2 • (0; 1) (−1; 0) (1; 0) • • x x -4 -2 2 4 -4 -2 2 4 (0; −1) • -2 -2 -4 -4 x2 − y2 = 1 y2 − x2 = 1 x2 − y2 = 1 is the unit hyperbola. Hyperbolic Functions: Similar to how the trigonometric functions, cosine and sine, correspond to the x and y values of the unit circle (x2 + y2 = 1), there are hyperbolic functions, hyperbolic cosine (cosh) and hyperbolic sine (sinh), which correspond to the x and y values of the right side of the unit hyperbola (x2 − y2 = 1). y y -1 1 x x π π 3π 2π π π 3π 2π 2 2 2 2 -1 -1 cos x sin x y y 6 2 4 x 2 -2 2 • (0; 1) -2 x -2 2 cosh x sinh x Hyperbolic Angle: Just like how the argument for the trigonometric functions is an angle, the argument for the hyperbolic functions is something called a hyperbolic angle. Instead of being defined by arc length, the hyperbolic angle is defined by area. If that seems confusing, consider the area of the circular sector of the unit circle. The r2θ equation for the area of a circular sector is Area = 2 , so because the radius of the unit circle is 1, any sector of the unit circle will have an area equal to half of the sector's central θ angle, A = 2 . -

Leonhard Euler - Wikipedia, the Free Encyclopedia Page 1 of 14
Leonhard Euler - Wikipedia, the free encyclopedia Page 1 of 14 Leonhard Euler From Wikipedia, the free encyclopedia Leonhard Euler ( German pronunciation: [l]; English Leonhard Euler approximation, "Oiler" [1] 15 April 1707 – 18 September 1783) was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion of a mathematical function.[2] He is also renowned for his work in mechanics, fluid dynamics, optics, and astronomy. Euler spent most of his adult life in St. Petersburg, Russia, and in Berlin, Prussia. He is considered to be the preeminent mathematician of the 18th century, and one of the greatest of all time. He is also one of the most prolific mathematicians ever; his collected works fill 60–80 quarto volumes. [3] A statement attributed to Pierre-Simon Laplace expresses Euler's influence on mathematics: "Read Euler, read Euler, he is our teacher in all things," which has also been translated as "Read Portrait by Emanuel Handmann 1756(?) Euler, read Euler, he is the master of us all." [4] Born 15 April 1707 Euler was featured on the sixth series of the Swiss 10- Basel, Switzerland franc banknote and on numerous Swiss, German, and Died Russian postage stamps. The asteroid 2002 Euler was 18 September 1783 (aged 76) named in his honor. He is also commemorated by the [OS: 7 September 1783] Lutheran Church on their Calendar of Saints on 24 St. Petersburg, Russia May – he was a devout Christian (and believer in Residence Prussia, Russia biblical inerrancy) who wrote apologetics and argued Switzerland [5] forcefully against the prominent atheists of his time. -

The Calculus of Trigonometric Functions the Calculus of Trigonometric Functions – a Guide for Teachers (Years 11–12)
1 Supporting Australian Mathematics Project 2 3 4 5 6 12 11 7 10 8 9 A guide for teachers – Years 11 and 12 Calculus: Module 15 The calculus of trigonometric functions The calculus of trigonometric functions – A guide for teachers (Years 11–12) Principal author: Peter Brown, University of NSW Dr Michael Evans, AMSI Associate Professor David Hunt, University of NSW Dr Daniel Mathews, Monash University Editor: Dr Jane Pitkethly, La Trobe University Illustrations and web design: Catherine Tan, Michael Shaw Full bibliographic details are available from Education Services Australia. Published by Education Services Australia PO Box 177 Carlton South Vic 3053 Australia Tel: (03) 9207 9600 Fax: (03) 9910 9800 Email: [email protected] Website: www.esa.edu.au © 2013 Education Services Australia Ltd, except where indicated otherwise. You may copy, distribute and adapt this material free of charge for non-commercial educational purposes, provided you retain all copyright notices and acknowledgements. This publication is funded by the Australian Government Department of Education, Employment and Workplace Relations. Supporting Australian Mathematics Project Australian Mathematical Sciences Institute Building 161 The University of Melbourne VIC 3010 Email: [email protected] Website: www.amsi.org.au Assumed knowledge ..................................... 4 Motivation ........................................... 4 Content ............................................. 5 Review of radian measure ................................. 5 An important limit .................................... -
18 3. EVALUATION of TRIGONOMETRIC FUNCTIONS in This Section, We Obtain Values of the Trigonometric Functions for Quadrantal
3. EVALUATION OF TRIGONOMETRIC FUNCTIONS In this section, we obtain values of the trigonometric functions for quadrantal angles, we introduce the idea of reference angles, and we discuss the use of a calculator to evaluate trigonometric functions of general angles. In Definition 2.1, the domain of each trigonometric function consists of all angles θ for which the denominator in the corresponding ratio is not zero. Because r > 0, it follows that sinθ = y/r and cosθ = x/r are defined for all angles θ . However, tanθ = y/x and secθ = r/x are not defined when the terminal side of θ lies anlong the y axis (so that x = 0). Likewise, cotθ = x/y and cscθ = r/y are not defined when the terminal side of θ lies along the x axis (so that y = 0). Therefore, when you deal with a trigonometric function of a quadrantal angle, you must check to be sure that the function is actually defined for that angle. Example 3.1 ---------------------------- ------------------------------------------------------------ Find the values (if they are defined) of the six trigonometric functions for the quadrantal angle θ = 90° (or θ = π 2 ). In order to use Definition 1, we begin by choosing any point ( 0 , y ) with y > 0, on the terminal side of the 90° angle (Figure 1). Because x = 0, it follows that tan 90° and sec 90° are undefined. Since y > 0, we have r = x2 + y 2 = 02 + y 2 = y 2 = y = y. y y x 0 Therefore, sin 90° = = = 1 cos 90° = = = 0 r y r y r y x 0 csc90° = = = 1 cot 90° = = = 0.