DOCSLIB.ORG

Central Meridian, Central to That Zone, to Which All Grid Lines Are Parallel Or Perpendicular

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Central Meridian, Central to That Zone, to Which All Grid Lines Are Parallel Or Perpendicular and continuingto84º latitude, (exceptforthemostnortherly 22. The UTM gridisfurtherdividedintotwentybands metres. Thedistancebetweenthegridlines shownistermedthe'gridinterval'. Depending on the scale of thechart,distancebet t at extended the pointfalls.SomeUTMgridzonesare terms of metres eastandnorthofthefalseor souther the for origins true and 10,000kmsouthofthe t on origins true false origins500kmwestofthe 500,000 metres eastand10,000,000northforthe false coordinateswhichare500,000metreseastand of the grid zones is theintersectionofitscentral meridian withtheequator.Eachgridoriginisassigned central meridian, central tothatzone,whichallgrid Each bandoflatitudeisgivenadesignationletterfr Grid ZoneDesignationAreasareillustratedinFig.10. GZD consists of the number oftheUTMgridzonefo bands. EachGridZoneDesignationAreaisidentifi 23. Grid ZoneDesignationAreasareformedbythein C D E F G H J K L M N P Q R S T U V W X 80º 72º 64º 56º 48º 40º 32º 24º 16º 08º 00º 08º 16º 24º 32º 40º 48º 56º 64º 72º 84º 180º 174º 168º 162º 156º 150º 144º 138º 132º 126º 120º N. 114º 108º 55º N to 64º N Nto64º 55º 72º N to 84º N N to84º 72º 102º Latitude Band 096º 090º 084º Zones Grid UTM Extended 1 Table 9-2 078º 072º 066º Revised Jul 10 060º band which coversthetwelvedegreesbetween 72º 9-2 Fig 10 The UTM Grid UTM The 10 Fig 9-2 054º 048º 042º AP3456 -9-2Position 036º 030º he equator,forthenorthernhemisphere,and500kmwest 024º Zone 35 34 33 32 31 31 36 37 018º 32 012º linesareparallelorperpendicular.Theoriginofeach om C to X(omittinglettersIandO)startingat80º igin inthehemisphereofUTMgridzonewhich ed by a unique Grid Zone Designation (GZD). The ed byauniqueGridZoneDesignation(GZD). E) Eto42º (33º 9º 006º llowed bythedesignationle ween thegridlinesshownis10,000,1,000or100 he expense of others. These are shown in Table 1. he expenseofothers.TheseareshowninTable1. n hemisphere.UTMGridcoordinatesaregivenin 000º 31 tersection of the UTMGridZonesandlatitude 0 metres north for the northern hemisphere, and hemisphere, 0 metresnorthforthenorthern 32 oflatitude.Eachbandcoverseightdegrees Page 10 of21 006º 012º 33 35 37 southern hemisphere.Thiseffectivelycreates 018º 12º 12º (9º E to 21º E) Eto21º (9º 12º 024º (3º 9º 9º (0º to 9º E) to9º (0º 9º E) to3º (0º 3º 030º (21º E to 33º E) Eto33º (21º Eliminated Eliminated 036º Eliminated 042º Width E to 12º E) E to12º 048º 054º 060º 066º 072º 078º 084º 090º 096º tter ofthelatitudeband. 102º 108º 114º 120º 126º 132º N and84º 138º 144º 150º 156º 162º 168º N). 174º S 180º AP3456 - 9-2 - Position 24. Each Grid Zone is sub-divided into columns and rows to form 100,000 metre (100 km) squares (Fig 11). Each column and row is given an identifying letter. Thus, each 100,000 metre square is identified by two letters corresponding to its column and row respectively. This pair of letters is termed the 100,000 metre square identification. Because the UTM Grid covers much of the Earth’s surface, 100,000 metre square identifications will be repeated. To identify individual 100,000 metre squares, the square identification is preceded by the grid zone designation. In Fig 11, it can be seen that there are two 100,000 metre squares designated YA but they are differentiated by the prefix of their UTM Grid Zone Designation Area, (in this case 3Q and 3N). The 100,000 metre squares are fitted into each 6º zone so that they are uniformly spaced about the central meridian of the zone and along the equator. As a result, the 'grid squares' along the borders of the 6º zones do not form squares. 9-2 Fig 11 Identification of 100 km Squares on the UTM Grid 180º 162º 24º 174º 168º 24º BG CG DG UG VG WG XG YG AG EG FG GG KM LM MM NM PM QM TG ZG HG JM RM SG YF BF CF DF EF FF GF KL LL ML NL PL QL TF UF VF WF XF AF ZF HF JL RL SF YE BE CE DE EE FE GE KK LK MK NK PK QK TE UE VE WE XE AE ZE HE JK RK SE XD YD BD CD DD ED FD HD KJ LJ MJ NJ PJ QJ TD UD VD WD AD ZD HD JJ RJ SD YC BC CC DC EC FC GC KH LH MH NH PH QH TC UC VC WC XC AC ZC HC JH RH SC YB BB CB DB EB FB GB KG LG MG NG PG QC TB UB VB WB XB AB ZB HB JG RG SB XA YA BA CA DA EA FA GA KF LF MF NF PF QF TA UA VA WA AA ZA 2,000,000 m HA JF RF SA 2,000,000 m XV YV BV CV DV EV FV GV KE LE ME NE PE QE TV UV VV WV AV ZV HV JE RE SV BU WU XU YU CU DU EU FU GU KD LD MD ND PD QD TU UU VU AU ZU 16º HU JD RD SU 16º WT XT YT BT CT DT ET FT GT KC LC MC NC PC QC TT UT VT AT ZT HT JC RC ST YS BS CS DS ES FS GS KB LB MB NB PB QB TS US VS WS XS AS ZS HS JB RB SS XR YR BR CR DR ER FR GR KA LA MA NA PA QA TR UR VR WR AR ZR HR JA RA SR BQ XQ YQ CQ DQ EQ FQ GQ KV LV MV NV PV QV TQ UQ VQ WQ AQ ZQ HQ JV RV SQ WP XP YP BP CP DP EP FP GP KU LU MU NU PU QU TP UP VP AP ZP HP JU RU SP BN CN VN WN XN YN DN EN FN GN KT LT MT NT PT QT TN UN AN ZN HN JT RT SN WM XM YM BM CM DM EM FM GM KS LS MS NS PS QS TM UM VM AM ZM HM JS RS SM AL BL CL DL UL VL WL XL YL ZL EL FL GL HL JR KR LR MR NR PR QR RR SL TL AK BK CK DK WK XK YK ZK EK FK GK HK JQ KQ LQ MQ NQ PQ QQ RQ SK TK UK VK 8º 8º AJ BJ CJ DJ WJ XJ YJ ZJ EJ FJ GJ HJ JP KP LP MP NP PP QP RP SJ TJ UJ VJ AH BH CH WH XH YH ZH DH EH FH GH HH JN KN LN MN NN PN QN RN SH TH UH VH AG BG CG ZG DG EG FG GG HG JM KM LM MM NM PM QM RM SG TG UG VG WG XG YG AF BF CF XF YF ZF DF EF FF GF HF JL KL LL ML NL PL QL RL SF TF UF VF WF AE BE CE DE EE YE ZE FE GE HE JK KK LK MK NK PK QK RK SE TE UE VE WE XE AD BD CD DD XD YD ZD ED FD GD HD JJ KJ LJ MJ NJ PJ QJ RJ SD TD UD VD WD AC BC XC YC ZC CC DC EC FC GC HC JH KH LH MH NH PH QH RH SC TC UC VC WC AB BB CB XB YB ZB DB EB FB GB HB JG KG LG MG NG PG QG RG SB TB UB VB WB AA BA CA DA WA XA YA ZA EA FA GA HA JF KF MF NF RF SA TA UA VA 0º LF PF QF 0º 180º 162º 174º 168º Revised Jul 10 Page 11 of 21 AP3456 - 9-2 - Position 25. Starting at the 180º meridian and moving eastwards for 18º along the equator, the 100,000 metre columns (including those along 6º zone borders) are lettered alphabetically from A to Z (with I and O omitted). This is repeated at 18º intervals. 26. In odd numbered UTM Grid Zones, the rows of 100,000 metre squares are lettered northwards alphabetically from A to V (with I and O omitted), the partial alphabet being repeated every 20 rows. In even numbered UTM Grid Zones, starting at the equator, the rows are lettered F to V (omitting I and O) followed by A to V (omitting I and O). This is done to increase the distance between 100,000 metre squares with the same square identification. Below the equator, the 100,000 metre rows are lettered northwards in such a way that they fit into the sequence of letters above in the same zone. THE UNIVERSAL POLAR STEREOGRAPHIC GRID Description of the Grid 27. The Universal Polar Stereographic Grid consists of two grids - one covering the North Polar area, (north of 84º N), and the other, the South Polar area (south of 80º S). These grids are based on a polar stereographic projection with the origin of each at the respective pole. The Northern and Southern UPS grids extend to 83º 30' N and 79º 30' S respectively to provide a 30' overlap with the UTM grid. Easting grid lines are parallel to the Greenwich Meridian (0º) and the 180º meridian. Northing grid lines are parallel to the 90º W and 90º E meridians. The grid origins are assigned false coordinates of 2,000,000 metres east and 2,000,000 metres north. When used in conjunction with the UTM grid the UPS Grids provide world-wide coverage. 28. The North polar area is divided into two parts by the Greenwich and 180º meridians (Fig 12). The half containing the West longitudes is given the grid zone designation Y whilst that containing the East longitude is given the grid designation Z. Similarly, the South polar area (Fig 13) is divided into two halves.
Load more

Recommended publications
  • Lat/Long/Size&Shape of Earth Name
    lat/long/size&shape of Earth Name: ____________________________________ Tuesday, September 23, 2008 1. Which statement provides the best evidence that Earth has a nearly spherical shape? 1. The Sun has a spherical shape. 3. Star trails photographed over a period of time show a circular pattern. 2. The altitude of Polaris changes in a definite pattern as an 4. The lengths of noontime shadows change observer's latitude changes. throughout the year. 2. Figure 1 The diagram represents Earth at a specific position in its orbit. Arrows indicate radiation from the Sun. Points A through D are locations on Earth's surface. As an observer travels from position B to position D, the altitude of Polaris in the nighttime sky will 1. decrease, only 3. increase, then decrease 2. increase, only 4. remain the same 3. How does the position of Polaris appear to change as an observer travels due north form the Equator? 1. The angle of Polaris above the northern horizon decreases. 3. Polaris appears to move westward. 2. The angle of Polaris above the northern horizon increases. 4. Polaris appears to move eastward. lat/long/size&shape of Earth 4. Precise measurements of Earth indicate that its polar diameter is 1. shorter than its equatorial diameter 2. longer than its equatorial diameter 3. the same length as its equatorial diameter 5. The best evidence that the Earth has a spherical shape is provided by 1. photographs of the Earth taken from space satellites 3. the changing orbital speed of the earth in its orbit around the Sun 2.
    [Show full text]
  • Gen Nav - P a G E | 1 15
    1. An aircraft departs from position A (04°10' S 178°22'W) and flies northward following the meridian for 2950 NM. It then flies westward along the parallel of latitude for 382 NM to position B. The coordinates of position B are? 45°00'N 172°38'E 2. The angle between the true great-circle track and the true rhumb-line track joining the following points: A (60° S 165° W) B (60° S 177° E), at the place of departure A, is: 7.8° 3. What is the time required to travel along the parallel of latitude 60° N between meridians 010° E and 030° W at a groundspeed of 480 kt? 2 HR 30 MIN 4. The duration of civil twilight is the time: Between sunset and when the centre of the sun is 6° below the true horizon 5. On the 27th of February, at 52°S and 040°E, the sunrise is at 0243 UTC. On the same day, at 52°S and 035°W, the sunrise is at: 0743 UTC 6. The rhumb-line distances between points A (60°00'N 002°30'E) and B (60°00'N 007°30'W) is: 300 NM 7. Given: TAS = 485 kt, OAT = ISA +10°C, FL 410. Calculate the Mach Number: 0.825 8. Given: Value for the ellipticity of the Earth is 1/297. Earth's semi-major axis, as measured at the equator, equals 6378.4 km. What is the semi-minor axis (km) of the earth at the axis of the Poles? 6 356.9 9.
    [Show full text]
  • People & Sites
    16 PEOPLE & SITES The People & Sites sections contain fields to help you provide contextual informa- tion for your collections. Artifacts, archival materials, photographs, and publica- tions reveal something about the people who made, used, owned, and collected them. People Biographies has fields to document the lives of the people whose stories your collections tell. Sites & Localities provides information about the locations from where items have been collected. When items’ catalog records are linked to Sites records with latitude and longitude or physical address fields com- pleted, you can map items’ site locations through Catalog Lists. PEOPLE BIOGRAPHIES The People field appears in all four catalogs and is used to identify people who appear in photographs or are associated with objects, archival materials and publica- tions. People Biographies enables you to record important information about these people, such as places of birth and death, parents, children, spouses, education, career, achievements, residences and relationships. People Biographies may be accessed from the People authority file as you enter data in catalog records. Each name entered in the People field automatically has an entry in the People authority file thus creating People Biography records. These records may also be opened directly from the Main Menu’s People & Sites section. 301 302 PastPerfect Museum Software User’s Guide From the Main Menu’s People & Sites section, click People Biographies. Figure 16-1 Click here to open the People People Biographies Biographies screen. on the Main Menu The Sidebar has Screen Views that enable you to view and complete biographical information, view catalog records, and use the custom, user defined fields.
    [Show full text]
  • Mercator's Projection
    Mercator's Projection: A Comparative Analysis of Rhumb Lines and Great Circles Karen Vezie Whitman College May 13, 2016 1 Abstract This paper provides an overview of the Mercator map projection. We examine how to map spherical and ellipsoidal Earth onto 2-dimensional space, and compare two paths one can take between two points on the earth: the great circle path and the rhumb line path. In looking at these two paths, we will investigate how latitude and longitude play an important role in the proportional difference between the two paths. Acknowledgements Thank you to Professor Albert Schueller for all his help and support in this process, Nina Henelsmith for her thoughtful revisions and notes, and Professor Barry Balof for his men- torship and instruction on mathematical writing. This paper could not have been written without their knowledge, expertise and encouragement. 2 Contents 1 Introduction 4 1.1 History . .4 1.2 Eccentricity and Latitude . .7 2 Mercator's Map 10 2.1 Rhumb Lines . 10 2.2 The Mercator Map . 12 2.3 Constructing the Map . 13 2.4 Stretching Factor . 15 2.5 Mapping Ellipsoidal Earth . 18 3 Distances Between Points On Earth 22 3.1 Rhumb Line distance . 22 3.2 Great Circle Arcs . 23 3.3 Calculating Great Circle Distance . 25 3.4 Comparing Rhumb Line and Great Circle . 26 3.5 On The Equator . 26 3.6 Increasing Latitude Pairs, Constant Longitude . 26 3.7 Increasing Latitude, Constant Longitude, Single Point . 29 3.8 Increasing Longitude, Constant Latitude . 32 3.9 Same Longitude . 33 4 Conclusion 34 Alphabetical Index 36 3 1 Introduction The figure of the earth has been an interesting topic in applied geometry for many years.
    [Show full text]
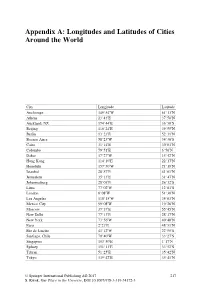
  • Appendix A: Longitudes and Latitudes of Cities Around the World
    Appendix A: Longitudes and Latitudes of Cities Around the World City Longitude Latitude Anchorage 149540W61130N Athens 23430E37580N Auckland, NZ 174440E36500S Beijing 116240E39550N Berlin 13230E52310N Buenos Aires 58230W34360S Cairo 31140E30030N Colombo 79510E6560N Dakar 17270W14420N Hong Kong 114100E22170N Honolulu 157500W21190N Istanbul 28570E41010N Jerusalem 35130E31470N Johannesburg 28030E26120S Lima 77020W12030S London 0080W51300N Los Angeles 118150W34030N Mexico City 99080W19260N Moscow 37370E55450N New Delhi 77130E28370N New York 73560W40400N Paris 2210E48510N Rio de Janeiro 43120W22550S Santiago, Chile 70400W33270S Singapore 103500E1170N Sydney 151130E33520S Tehran 51250E35420N Tokyo 139420E35410N © Springer International Publishing AG 2017 217 S. Kwok, Our Place in the Universe, DOI 10.1007/978-3-319-54172-3 Appendix B: Astronomical Measurements Ancient astronomers typically made two types of measurements: position and brightness. Position refers to the angular position of a celestial object on the celestial sphere. Since our view of the sky is two-dimensional, we use the unit of angles to assign the positions of stars. The Babylonian concept of a degree is based on the fact that 1 year has 365 days. Since 365 is close to the nice number 360 which can be divided by 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, etc., astronomers adopted 360 degrees as a full circle and this Babylonian unit is still in use today. Again, since 60 is a good number, we divide a degree into 60 arc minutes, and an arc minute into 60 arc seconds. To get an idea of how large these units are, a one-centimeter coin placed at a distance of 1 km will have an angular size of 2 arc seconds, so one arc second is a very small separation indeed.
    [Show full text]
  • Building Geography Skills for Life
    Glencoe Building Geography Skills for Life Student Text-Workbook Richard G. Boehm, Ph.D. Professor of Geography and Jesse H. Jones Distinguished Chair in Geographic Education Department of Geography Southwest Texas State University San Marcos, Texas Acknowledgments The Global Pencil lesson on pages 151–153 is an adaptation of “The International Pencil: Elementary Level Unit on Global Interdependence,” by Lawrence C. Wolken, Journal of Geography, November/December, 1984, pp. 290–293. Used by permission. Photo Credits 6 PhotoDisc; 60 PhotoDisc; 77 PhotoDisc; 81 PhotoDisc; 84 PhotoDisc; 98 PhotoDisc; 109 PhotoDisc; 113 PhotoDisc; 118 PhotoSpin, Inc.; 143 PhotoDisc; 147 PhotoDisc; 152 PhotoDisc; 158 PhotoDisc; 178 PhotoDisc; 181 Shepard Sherbell/CORBIS; 183 PhotoDisc; 187 PhotoDisc; 194 PhotoDisc; 208 PhotoDisc. Cover David Teal/CORBIS Copyright © by the McGraw-Hill Companies, Inc. All rights reserved. Permission is granted to reproduce the material contained herein on the condition that such material be reproduced only for classroom use; be provided to students, teachers, and families without charge; and be used solely in conjunction with Building Geography Skills for Life. Any other reproduction, for use or sale, is prohibited without prior written permission of the publisher. Send all inquiries to: Glencoe/McGraw-Hill 8787 Orion Place Columbus, Ohio 43240-4027 Printed in the United States of America. ISBN 0-07-825799-9 (Student Text-Workbook) ISBN 0-07-825800-6 (Teacher Annotated Edition) 2 3 4 5 6 7 8 9 10 047 08 07 06 05 04 03 02 Table of Contents To the Student. 5 UNIT 1 The World in Spatial Terms . 6 Lesson 1: Direction and Distance .
    [Show full text]
  • Mining and Natural Resources
    LATITUDE AND LONGITUDE Introduction to Coordinate Systems on Earth This exercise is an introduction to a standardized coordinate system used throughout the world for centuries, Latitude and Longitude. While there are many coordinate systems that have been developed for a variety of mapping and geographic purposes, the great majority of maps produced for public use still rely on the traditional Latitude and Longitude system. Fig. 1. Google Earth display of Earth with overlaid latitude/longitude grid. In Google Earth, you can toggle the latitude/longitude grid on/off from the menu bar at the top of the page. Move your cursor to the ‘View’ option on the menu bar and click it. Locate the Lat/Lon Grid option and click it. You will see the latitude/longitude grid appear on the Earth image in Google Earth. Clicking on the Lat/Lon Grid option again will turn off the grid. Alternatively, you can toggle the latitude/longitude grid by simultaneously using the ‘ctrl + L’ keys on your keyboard. In the latitude/longitude system, the nearly spherical Earth is divided into a grid composed of parallels of latitude (North-South grid lines) and meridians of longitude (East-West grid lines). The equator serves as the reference line for latitude and was arbitrarily assigned a value of 0 degrees centuries ago. Latitude is then measured in degrees north or south from the equator. 1. What is the angular distance from the South Pole to the North Pole? 2. What is the angular distance from the Equator to the South Pole? 1 3. What is the angular distance from the Equator to the North Pole? Longitude is measured in degrees east or west from the Prime Meridian (rotate the Google Earth globe to locate the Prime Meridian).
    [Show full text]
  • Understanding Our World Through Geography. Activities Good
    DOCUMENT RESUME ED 394 877 SO 026 091 AUTHOR Aten, Jerry TITLE Understanding Our World through Geography. activities To Improve Geography Skills and Promote Ecology. REPORT NO ISBN-0-86653-592-6 PUB DATE 91 NOTE 234p. AVAILABLE FROMGood Apple, 1204 Buchanan, Box 299, Carthage, IL 62321-0299. PUB TYPE Guides Classroom Use Teaching Guides (For Teacher) (052) Guides Classroom Use Instructional Materials (For Learner) (051) EDRS PRICE MF01/PC10 Plus Postage. DESCRIPTORS Area Studies; *Ecology; Elementary Education; *Geographic Concepts; *Geography; *Geography Instruction; Global Education; *Maps; *Map Skills; *Social Studies ABSTRACT This book focuses on improving geography skills and knowledge of basic concepts for grades 4-8, through a variety of activities and resources. The book is divided into six s.:,ctions that combine to make it convenient for use. The sections include: (1) "Map Reading Skills";(2) "Geography Concepts and Definitions"; (3) "Peoples of the Florid";(4) "A Planet in Peril";(5) "Geowords"; and (6) "Map Section." The messages of conservation and ecology are empowering to students as they address the future of the planet. (EH) *********************************************************************** * Reproductions supplied by EDRS are the best that can be made from the original document. *********************************************************************** rr' s- c;r: T-71aff:C" I 1 . .. ".... /.., . ' . A --. ..,,, y -... .71,- ?,'..'".. -.....A." '' ,"4,^ _ ..1 : V .'-. il/ .:t .. -- , ,-.----4-1--- ,-, ,1,....... ----,.,r
    [Show full text]
  • Map Reading and Land Navigation
    HEADQUARTERS FM 3-25.26 (FM 21-26) DEPARTMENT OF THE ARMY MAP READING AND LAND NAVIGATION DISTRIBUTION RESTRICTION: Approved for public release; distribution is unlimited. FM 3-25.26 PREFACE The purpose of this field manual is to provide a standardized source document for Armywide reference on map reading and land navigation. This manual applies to every soldier in the Army regardless of service branch, MOS, or rank. This manual also contains both doctrine and training guidance on these subjects. Part One addresses map reading and Part Two, land navigation. The appendixes include a list of exportable training materials, a matrix of land navigation tasks, an introduction to orienteering, and a discussion of several devices that can assist the soldier in land navigation. The proponent of this publication is the US Army Infantry School. Submit changes to this publication on DA Form 2028 (Recommended Changes to Publications and Blank Forms) directly to Commandant US Army Infantry School ATTN: ATSH-IN-S3 Fort Benning, GA 31905-5596. [email protected] Unless this publication states otherwise, masculine nouns and pronouns do not refer exclusively to men. v FM 3-25.26 (FM 21-26) FIELD MANUAL HEADQUARTERS No. 3-25.26 DEPARTMENT OF THE ARMY Washington, DC , 20 July 2001 MAP READING AND LAND NAVIGATION CONTENTS Page PREFACE.......................................................................................................................... v Part One MAP READING CHAPTER 1. TRAINING STRATEGY 1-1. Building-Block Approach .........................................................1-1 1-2. Armywide Implementation .......................................................1-2 1-3. Safety.........................................................................................1-2 CHAPTER 2. MAPS 2-1. Definition ..................................................................................2-1 2-2. Purpose......................................................................................2-1 2-3.
    [Show full text]
  • Rare Plant Survey Tips
    Rare Plant Monitoring Steward Handbook THE GLOBAL POSITIONING SYSTEM Bill Eichelberger 4/21/2004 With additional information about UTM coordinates by Brian Kurzel 6/14/2007 The Global Positioning System (GPS) is a group of satellites built and maintained by the United States to provide accurate positioning information at any point on the earth. The GPS Constellation consists of 24 satellites that orbit the earth at an altitude of 11,000 nautical miles, taking 12 hours per revolution. This constellation provides the user with between five and eight satellites visible at all times from any point on the earth. A GPS receiver picks up the signal from the satellites and performs some complex calculations to determine the latitude and longitude of the location of the receiver. The following map shows the earth with imaginary lines of latitude and longitude drawn on it. You will note that zero latitude is the equator and zero longitude is the Prime Meridian that passes through Greenwich, England. Another grid that is often used to locate features on the earth is Universal Transverse Mercator (see UTM handout). The basic thing the receiver does is to display coordinates of locations on the earth (including latitude/longitude or UTM coordinates), although all GPS receivers can use this information to provide many other functions. The following are summaries of GPS coordinates in the two main systems. Latitude and Longitude The receiver displays degrees, minutes, and decimal fractions of minutes. Look at the coordinates showing on your GPS. This will be shown in this format: N 39° 43.933’ W104° 57.628’ On the map above, that would be roughly on the E in North America.
    [Show full text]
  • Mapping and Fur Seal Migration Track OBJECTIVE Move in a Straight Line
    Laaquda�x: The Northern Fur Seal LESSON SIX GEOGRAPHY ACTIVITY 6.3 Grade Level 4–6 Mapping and Fur Seal Migration Track OBJECTIVE move in a straight line. If food is hard to find they will move out of the area. If food is abundant, they will stay Students will become familiar with basic concepts of in the area. geography. Students will analyze a northern fur seal migration track. MATERIALS TIME REQUIRED • World globe (teacher provided) 20- 30 minutes • Diagram of Prime Meridian, Arctic Circle, Tropic of Cancer • Yarn or string (teacher provided) BACKGROUND • Map of adult female fur seal migration track Geography Every place on the earth can be described using two numbers, latitude and longitude. In order to accurately PROCEDURES – GEOGRAPHY pinpoint locations on the surface of the earth, humans Orientation created a geographical grid system using lines of • On the globe, show students latitude and longitude latitude and lines of longitude. This grid is attached to lines. two fixed points, the North Pole and the South Pole. • Have them find the North Pole, South Pole, and Latitude lines run around the globe parallel to the Pribilof Islands. equator. They measure the distance north and • Have students find the Arctic Circle and the Tropic south of the equator. of Cancer. What latitude are they? Arctic Circle (66.5° N) Longitude lines (or meridians) are arcs running from Tropic of Cancer (23.5° N) the North Pole to the South Pole. They measure distances east and west from a base line or • Have students find the equator, Tropic of Capricorn, prime meridian.
    [Show full text]
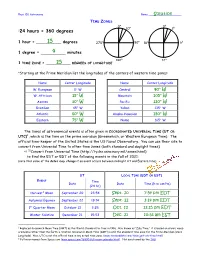
  • Latitude, Longitude and Time Zones
    Phys 102 Astronomy Name ____________________Solution TIME ZONES 0° 0h 30° 2h 324 hours = 360 degrees 1 hour = __________15 degrees 270° 90° 18h 6h 1 degree = __________4 minutes 180° 12h 1 TIME ZONE = __________15 DEGREES OF LONGITUDE 6Starting at the Prime Meridian list the longitudes of the centers of western time zones: Name Center Longitude Name Center Longitude W. European 0° W Central 90° W W. Aftrican 15° W Mountain 105° W Azores 30° W Pacific 120° W Brazilian 45° W Yukon 135° W Atlantic 60° W Alaska-Hawaiian 150° W Eastern 75° W Nome 165° W The times of astronomical events is often given in COORDINATED UNIVERSAL TIME (UT OR UTC)1, which is the time on the prime meridian (Greenwhich, or Western European Time). The official time-keeper of the United States is the US Naval Observatory. You can use their site to convert from Universal Time to other time zones (both standard and daylight times) 12Convert from Universal Time (http://tycho.usno.navy.mil/zones.html) to find the EST or EDT of the following events in the fall of 2021: (note that some of the dates may change if an event occurs between midnight UT and Eastern time) UT LOCAL TIME (EDT OR EST) EVENT Time Date Date Time (h:m AM/PM) (24 hr) Harvest2 Moon September 20 23:54 Sept. 20 7:54 pm EDT Autumnal Equinox September 22 19:14 Sept. 22 3:14 pm EDT 1st Quarter Moon October 13 3:25 Oct. 12 11:25 pm EDT Winter Solstice December 21 15:53 Dec.
    [Show full text]