DOCSLIB.ORG

Appendix a Symmetry Groups

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Appendix a Symmetry Groups Appendix A Symmetry Groups A mathematical group G is a set of objects (the group's elements) with a binary op- eration denoted by "+" or by "*" defined on the elements that satisfies the following requirements. 1. Closure: for any a, b G G, the sum (a + b) is an element of G. 2. Associativity: any a,b,c G G satisfies (a + b) + c = a + (b + c). 3. Identity: there exists e G G such that for all a G (7 (a + e) = (e + a) = a. 4. Inverses: for each a G G, there exists a unique element a~l G G such that a-fa"1 — a"1 + a = e. 5. If the group operation is commutative, i.e., if a + b = b + a for any a,b £ G, the group is called Abelian. Question: What's purple and commutes? Answer: An Abelian grape. Examples of groups: 1. The set of all the integers with integer addition. The identity element is the integer 0. This is an infinite group. 2. The (finite) set of the integers 0, 1, 2,... ,m — 1 with modulo-m addition. 3. The integers 1, 2,. .. ,g — 1 for a prime q with modulo-g multiplication. 4. The set of all rotations in two dimensions under the operation: The sum of the two rotations by a and (3 degrees is a rotation by a + (3 degrees. The set (0,1, 2,3) with modulo-4 addition is a group denoted by G(4). It obeys the 448 Appendix A Symmetry Groups addition table + 0 1 2 3 0 0 1 2 3 1 1 2 3 0 2 2 3 0 1 3 3 0 1 2 The order of a group (its cardinality) is the number of elements. It is denoted by ord(G). The order of G(4) is 4. A subgroup is a subset of the elements of a group that is closed under the group's operation. A theorem by Lagrange states that if S is a subgroup of G, then ord(5) divides ord(G). For example, if S is the subgroup (0,1) of G(4), then ord(5) = 2 divides ord(G(4)) = 4 and G(4) can be partitioned into the cosets S and S + 2. This appendix deals with symmetry groups. The elements of such a group are sym- metry operations (or transformations) on an object; they are not numbers. Figure A.la shows four symmetric objects: a rhombus, a rectangle, a square, and a pentagon. The term symmetric means an object that retains its shape and location under certain trans- formations. A square, for example, is highly symmetric, because it preserves its shape and position when rotated by a multiple of 90° or when reflected about the four axes shown by dashed lines in Figure A.lb. A rectangle is less symmetric because a rotation of 90° changes its shape from horizontal to vertical or vice versa. b a b a b c d c (a) (b) c) Figure A.I: Symmetries of Rhombus, Square, and Pentagon. For simple geometric objects, it is possible to express rotations and reflections by listing the new position of each vertex of the object. When the square is rotated 90° clockwise, for example, vertex a moves to b, b moves to c, and so on, which can be expressed as the permutation ab c dN b c d a Symmetry Groups 449 Reflections of the square about a vertical axis and about the main diagonal are expressed by a b c d \ /abed' bade/' Vadcb The connection between symmetry transformations and groups becomes clear when we consider combinations of transformations. The rectangle is transformed to itself after (1) a 0° rotation, (2) a reflection about a central horizontal axis, (3) a reflection about a central vertical axis, and (4) a 180° rotation. Examining the diagram, the following properties become clear: 1. Transformation 1 followed by transformation i (or i followed by 1) is equivalent to just transformation i for any i. 2. Any of the four transformations followed by itself returns the rectangle to its original shape, so it is identical to transformation 1. 3. Transformation 3 followed by 2 is equivalent to 4. An analysis of all the combinations of two transformations of the rectangle yields Table A.2a. The table can be considered the definition of a symmetry group of four ele- ments, because it specifies the group operation for the elements. A direct check verifies that element 1 (the null transformation) is the group's identity, that the operation is closed, and that it is noncommutative. This symmetry group is denoted by D4 (D for dihedral, meaning bending the arms up; anhedral means the opposite). (A dihedral group is a group whose elements correspond to a closed set of rotations and reflections in the plane. The dihedral group with 2n elements is denoted by either Dn or D2n- The group consists of n reflections, n — 1 rotations, and the identity transformation.) * 0 1 2 3 4 5 6 7 8 9 0 0 1 2 3 4 5 6 7 8 9 * 0 1 2 3 4 5 6 7 1 1 2 3 4 0 6 7 8 9 5 0 0 1 2 3 4 5 6 7 2 2 3 4 0 1 7 8 9 5 6 1 1 2 3 0 6 7 5 4 3 3 4 0 1 2 8 9 5 6 7 2 2 3 0 1 5 4 7 6 4 4 0 1 2 3 9 5 6 7 8 * 1 2 3 4 3 3 0 1 2 7 6 4 5 5 5 9 8 7 6 0 4 3 2 1 1 1 2 3 4 4 4 7 5 6 0 2 3 1 6 6 5 9 8 7 1 0 4 3 2 2 2 1 4 3 5 5 6 4 7 2 0 1 3 7 7 6 5 9 8 2 1 0 4 3 3 3 4 1 2 6 6 4 7 5 1 3 0 2 8 8 7 6 5 9 3 2 1 0 4 4 4 3 2 1 7 7 5 6 4 3 1 2 0 9 9 8 7 6 5 4 3 2 1 0 (a) (b) (c) Table A.2: The D4, D%, and D10 Symmetry Groups. Similarly, the rhombus has limited symmetry. Its four symmetry transformations are (1) the null transformation, (2) a reflection about the line bd, (3) a reflection about 450 Appendix A Symmetry Groups line ac, and (4) a 180° rotation. An analysis of all the combinations of two of these transformations, however, results in the same symmetry group. Thus, even though the rhombus and rectangle are different objects and their symmetry transformations are different, we can say that they have the same symmetries and we call them isometric. Intuitively, a square is more symmetric than a rectangle or a rhombus. There are more transformations that leave it unchanged. It is easy to see that these are the four rotations by multiples of 90° and the four reflections about the vertical, horizontal, and two diagonal axes. These eight transformations can be written as the permutations _/abcd\ _ /abcd\ _ /ab c d\ _ / a b c d ~ \abcdj' "ybcday5 \cdaby' ""\dabc __/abcd\ /abcd\ /ab cd\ 7 __ /^ a ^ c d ybadcy' ydcbay yadcby ycbad which can immediately be used to construct the symmetry dihedral group Dg listed in Table A.2b. Finally, the pentagon is used to create the larger symmetry group Dio, because it has 10 symmetry transformations. Figure A.la shows that the pentagon is transformed to itself by any rotation through a multiple of 60°, while Figure A.lc shows that it can be symmetrically reflected about five different axes. These ten transformations give rise to the DIQ symmetry group of Table A.2c (identical to Table 2.14a), and it is this group that is used by the Verhoeff check digit method of Section 2.11. The mathematical sciences particularly exhibit order, symmetry, and limitation; and these are the greatest forms of the beautiful. —Aristotle, Metaphysica Appendix B Galois Fields This appendix is an introduction to finite fields for those who need to brush up on this topic. Finite fields are used in cryptography in the Rijndael (AES) algorithm and in stream ciphers. In the field of error-control codes, they are used extensively. The Reed-Solomon codes of Section 1.14 operate on the elements of such a field. B.I Field Definitions and Operations The mathematical concept of a field is based on that of a group, which has been intro- duced at the start of Appendix A. A field F is a set with two operations—addition "+" and multiplication ax"—that satisfies the following conditions. 1. F is an Abelian group under the 4- operation. 2. F is closed under the x operation. 3. The nonzero elements of F form an Abelian group under x. 4. The elements obey the distributive law (a -{- b)xc ~ axc-{- bxc. Examples of fields are 1. The real numbers under the normal addition and multiplication; 2. The complex numbers; and 3. The rational numbers. Notice that the integers do not form a field under addition and multiplication because the multiplicative inverse (reciprocal) of an integer a is I/a, which is generally a noninteger. Also, a finite set of real numbers is not a field under normal addition and multiplication because these operations can create a result outside the set.
Load more

Recommended publications
  • A Covert Encryption Method for Applications in Electronic Data Interchange
    Technological University Dublin ARROW@TU Dublin Articles School of Electrical and Electronic Engineering 2009-01-01 A Covert Encryption Method for Applications in Electronic Data Interchange Jonathan Blackledge Technological University Dublin, [email protected] Dmitry Dubovitskiy Oxford Recognition Limited, [email protected] Follow this and additional works at: https://arrow.tudublin.ie/engscheleart2 Part of the Digital Communications and Networking Commons, Numerical Analysis and Computation Commons, and the Software Engineering Commons Recommended Citation Blackledge, J., Dubovitskiy, D.: A Covert Encryption Method for Applications in Electronic Data Interchange. ISAST Journal on Electronics and Signal Processing, vol: 4, issue: 1, pages: 107 -128, 2009. doi:10.21427/D7RS67 This Article is brought to you for free and open access by the School of Electrical and Electronic Engineering at ARROW@TU Dublin. It has been accepted for inclusion in Articles by an authorized administrator of ARROW@TU Dublin. For more information, please contact [email protected], [email protected]. This work is licensed under a Creative Commons Attribution-Noncommercial-Share Alike 4.0 License A Covert Encryption Method for Applications in Electronic Data Interchange Jonathan M Blackledge, Fellow, IET, Fellow, BCS and Dmitry A Dubovitskiy, Member IET Abstract— A principal weakness of all encryption systems is to make sure that the ciphertext is relatively strong (but not that the output data can be ‘seen’ to be encrypted. In other too strong!) and that the information extracted is of good words, encrypted data provides a ‘flag’ on the potential value quality in terms of providing the attacker with ‘intelligence’ of the information that has been encrypted.
    [Show full text]
  • Improved Cryptosystem Using SDES Algorithm with Substitution Ciphers G.Suman * , Ch
    Volume 3, Issue 7, July 2013 ISSN: 2277 128X International Journal of Advanced Research in Computer Science and Software Engineering Research Paper Available online at: www.ijarcsse.com Improved Cryptosystem Using SDES Algorithm with Substitution Ciphers G.Suman * , Ch. Krishna M. Tech (SE) & SNIST. India Abstract— Security is playing a very important and crucial role in the field of network communication system and Internet. Simplified Data encryption standard (SDES) is a private key cryptography system that provides the security in communication system but now a days the advancement in the computational power the SDES seems to be weak against the brute force attacks. To improve the security of SDES algorithm the substitution techniques are added before the SDES algorithm to perform its process. By using an Improved Cryptosystem the security has been improved which is very crucial in the communication and field of Internet. If the substitution techniques are used before the original SDES algorithm then the intruder required first to break the original SDES algorithm and then substitution techniques. So the security is more as compared to a SDES algorithm. Keywords— Cipher text, Decryption, SDES, Encryption, Plain text, OPBFT,OPBTS ,Substitution. I. Introduction The process of encoding the plaintext into cipher text is called Encryption and the process of decoding ciphers text to plaintext is called Decryption. This can be done by two techniques symmetric-key cryptography and asymmetric key cryptography. Symmetric key cryptography involves the usage of the same key for encryption and decryption. But the Asymmetric key cryptography involves the usage of one key for encryption and another different key for decryption.
    [Show full text]
  • Cryptography Using Steganography: New Algorithms and Applications
    Technological University Dublin ARROW@TU Dublin Articles School of Electrical and Electronic Engineering 2011 Cryptography Using Steganography: New Algorithms and Applications Jonathan Blackledge Technological University Dublin, [email protected] Follow this and additional works at: https://arrow.tudublin.ie/engscheleart2 Part of the Dynamic Systems Commons, and the Theory and Algorithms Commons Recommended Citation Blackledge, J. (2011) Cryptography and Steganography: New Algorithms and Applications. Lecture Notes, Centre for Advanced Studies, Warsaw University of Technology, Warsaw, 2011. doi:10.21427/D7ZS63 This Article is brought to you for free and open access by the School of Electrical and Electronic Engineering at ARROW@TU Dublin. It has been accepted for inclusion in Articles by an authorized administrator of ARROW@TU Dublin. For more information, please contact [email protected], [email protected], [email protected]. This work is licensed under a Creative Commons Attribution-Noncommercial-Share Alike 3.0 License Cryptography and Steganography: New Algorithms and Applications Prof. Dr. Jonathan Blackledge Science Foundation Ireland Stokes Professor School of Electrical Engineering Systems Dublin Institute of Technology Distinguished Professor Centre for Advanced Studies Warsaw University of Technology http://eleceng.dit.ie/blackledge http://jmblackledge.web.officelive.com [email protected] [email protected] Editor: Stanislaw Janeczko Technical editors: Malgorzata Zielinska, Anna Zubrowska General layout and cover design: Emilia Bojanczyk c Centre for Advanced Studies, Warsaw University of Technology, Warsaw 2011 For additional information on this series, visit the CAS Publications Website at http://www.csz.pw.edu.pl/index.php/en/publications ISBN: 978-83-61993-01-83 Pinted in Poland Preface Developing methods for ensuring the secure exchange of information is one of the oldest occupations in history.
    [Show full text]
  • Rhyming Dictionary
    Merriam-Webster's Rhyming Dictionary Merriam-Webster, Incorporated Springfield, Massachusetts A GENUINE MERRIAM-WEBSTER The name Webster alone is no guarantee of excellence. It is used by a number of publishers and may serve mainly to mislead an unwary buyer. Merriam-Webster™ is the name you should look for when you consider the purchase of dictionaries or other fine reference books. It carries the reputation of a company that has been publishing since 1831 and is your assurance of quality and authority. Copyright © 2002 by Merriam-Webster, Incorporated Library of Congress Cataloging-in-Publication Data Merriam-Webster's rhyming dictionary, p. cm. ISBN 0-87779-632-7 1. English language-Rhyme-Dictionaries. I. Title: Rhyming dictionary. II. Merriam-Webster, Inc. PE1519 .M47 2002 423'.l-dc21 2001052192 All rights reserved. No part of this book covered by the copyrights hereon may be reproduced or copied in any form or by any means—graphic, electronic, or mechanical, including photocopying, taping, or information storage and retrieval systems—without written permission of the publisher. Printed and bound in the United States of America 234RRD/H05040302 Explanatory Notes MERRIAM-WEBSTER's RHYMING DICTIONARY is a listing of words grouped according to the way they rhyme. The words are drawn from Merriam- Webster's Collegiate Dictionary. Though many uncommon words can be found here, many highly technical or obscure words have been omitted, as have words whose only meanings are vulgar or offensive. Rhyming sound Words in this book are gathered into entries on the basis of their rhyming sound. The rhyming sound is the last part of the word, from the vowel sound in the last stressed syllable to the end of the word.
    [Show full text]
  • Transposition Cipher in Cryptography, a Transposition Cipher Is a Method of Encryption by Which the Positions Held by Units of P
    Transposition cipher In cryptography, a transposition cipher is a method of encryption by which the positions held by units of plaintext (which are commonly characters or groups of characters) are shifted according to a regular system, so that the ciphertext constitutes a permutation of the plaintext. That is, the order of the units is changed. Mathematically a bijective function is used on the characters' positions to encrypt and an inverse function to decrypt. Following are some implementations. Contents • 1 Rail Fence cipher • 2 Route cipher • 3 Columnar transposition • 4 Double transposition • 5 Myszkowski transposition • 6 Disrupted transposition • 7 Grilles • 8 Detection and cryptanalysis • 9 Combinations • 10 Fractionation Rail Fence cipher The Rail Fence cipher is a form of transposition cipher that gets its name from the way in which it is encoded. In the rail fence cipher, the plaintext is written downwards on successive "rails" of an imaginary fence, then moving up when we get to the bottom. The message is then read off in rows. For example, using three "rails" and a message of 'WE ARE DISCOVERED. FLEE AT ONCE', the cipherer writes out: W . E . C . R . L . T . E . E . R . D . S . O . E . E . F . E . A . O . C . A . I . V . D . E . N . Then reads off: WECRL TEERD SOEEF EAOCA IVDEN (The cipherer has broken this ciphertext up into blocks of five to help avoid errors.) Route cipher In a route cipher, the plaintext is first written out in a grid of given dimensions, then read off in a pattern given in the key.
    [Show full text]
  • Substitution Cipher in Cryptography, a Substitution Cipher Is a Method Of
    Substitution cipher In cryptography, a substitution cipher is a method of encryption by which units of plaintext are replaced with ciphertext according to a regular system; the "units" may be single letters (the most common), pairs of letters, triplets of letters, mixtures of the above, and so forth. The receiver deciphers the text by performing an inverse substitution. Substitution ciphers can be compared with transposition ciphers. In a transposition cipher, the units of the plaintext are rearranged in a different and usually quite complex order, but the units themselves are left unchanged. By contrast, in a substitution cipher, the units of the plaintext are retained in the same sequence in the ciphertext, but the units themselves are altered. There are a number of different types of substitution cipher. If the cipher operates on single letters, it is termed a simple substitution cipher; a cipher that operates on larger groups of letters is termed polygraphic. A monoalphabetic cipher uses fixed substitution over the entire message, whereas a polyalphabetic cipher uses a number of substitutions at different times in the message, where a unit from the plaintext is mapped to one of several possibilities in the ciphertext and vice-versa. Contents • 1 Simple substitution o 1.1 Examples o 1.2 Security for simple substitution ciphers • 2 Homophonic substitution • 3 Polyalphabetic substitution • 4 Polygraphic substitution • 5 Mechanical substitution ciphers • 6 The one-time pad • 7 Substitution in modern cryptography • 8 Substitution ciphers in popular culture Simple substitution 1 ROT13 is a Caesar cipher, a type of substitution cipher. In ROT13, the alphabet is rotated 13 steps.
    [Show full text]
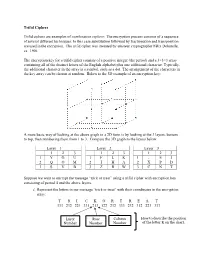
  • Trifid Ciphers
    Trifid Ciphers Trifid ciphers are examples of combination ciphers: The encryption process consists of a sequence of several different techniques. In this case substitution followed by fractionation and transposition are used in the encryption. The trifid cipher was invented by amateur cryptographer F´elix Delastelle, ca. 1900. The encryption key for a trifid cipher consists of a positive integer (the period) and a 3×3×3 array containing all of the distinct letters of the English alphabet plus one additional character. Typically, the additional character in the array is a symbol, such as a dot. The arrangement of the characters in the key array can be chosen at random. Below is the 3D example of an encryption key: A more basic way of looking at the above graph in a 2D form is by looking at the 3 layers, bottom to top, then numbering them from 1 to 3. Compare the 3D graph to the layers below. Layer 1 Layer 2 Layer 3 1 2 3 1 2 3 1 2 3 1 Y G U 1 F L K 1 . E J 2 Q O M 2 I H A 2 X P D 3 S V B 3 Z R W 3 C N T Suppose we want to encrypt the message “trick or treat” using a trifid cipher with encryption key consisting of period 4 and the above layers. i. Represent the letters in our message “trick or treat” with their coordinates in the encryption array: T R I C K O R T R E A T 333 232 221 331 213 122 232 333 232 312 223 333 Layer Row Column How to describe the position Number Number Number of the letter K on the chart.
    [Show full text]
  • 2. Classic Cryptography Methods 2.1. Spartan Scytale. One of the Oldest Known Examples Is the Spartan Scytale (Scytale /Skɪtəl
    2. Classic Cryptography Methods 2.1. Spartan scytale. One of the oldest known examples is the Spartan scytale (scytale /skɪtəli/, rhymes with Italy, a baton). From indirect evidence, the scytale was first mentioned by the Greek poet Archilochus who lived in the 7th century B.C. (over 2500 years ago). The ancient Greeks, and the Spartans in particular, are said to have used this cipher to communicate during military campaigns.Sender and recipient each had a cylinder (called a scytale) of exactly the same radius. The sender wound a narrow ribbon of parchment around his cylinder, then wrote on it lengthwise. After the ribbon is unwound, the writing could be read only by a person who had a cylinder of exactly the same circumference. The following table illustrate the idea. Imagine that each column wraps around the dowel one time, that is that the bottom of one column is followed by the top of the next column. Original message: Kill king tomorrow midnight Wrapped message: k i l l k i n g t o m o r r o w m i d n i g h t Encoded message: ktm ioi lmd lon kri irg noh gwt The key parameter in using the scytale encryption is the number of letters that can be recorded on one wrap ribbon around the dowel. Above the maximum was 3, since there are 3 rows in the wrapped meassage. The last row was padded with blank spaces before the message was encoded. We'll call this the wrap parameter. If you don't know the wrap parameter you cannot decode a message.
    [Show full text]
  • Polybius Square in Cryptography: a Brief Review of Literature
    ISSN 2278-3091 Jan Carlo T. Arroyo et al., International Journal ofVolume Advanced 9, Trends No.3, in May Computer - June Science 2020 and Engineering, 9(3), May – June 2020, 3798 – 3808 International Journal of Advanced Trends in Computer Science and Engineering Available Online at http://www.warse.org/IJATCSE/static/pdf/file/ijatcse198932020.pdf https://doi.org/10.30534/ijatcse/2020/198932020 Polybius Square in Cryptography: A Brief Review of Literature Jan Carlo T. Arroyo1, Cristina E. Dumdumaya2, Allemar Jhone P. Delima3 1,3College of Computing Education, University of Mindanao, Davao City, Davao del Sur, Philippines 1,2College of Information and Computing, University of Southeastern Philippines, Davao City, Davao del Sur, Philippines 3College of Engineering, Technology and Management, Cebu Technological University-Barili Campus, Cebu, Philippines [email protected], [email protected], [email protected] concerns data integrity, confidentiality, authentication to a ABSTRACT wireless communication system, and several other security services where information transfer between different users Cryptography is a method to secure sensitive data for storage takes place [10]–[12]. To protect the information, data are and communication in the presence of third parties called transformed into an unintelligible format using varied cipher adversaries. One of the first recorded incidents of technologies [15]. Maintaining data integrity and security is cryptography occurred in Ancient Rome, where the Polybius done through cipher whose bottleneck for an optimal cipher, also known as Polybius square, was developed. The implementation relies on the cipher used. A cipher is an Polybius cipher has been used as an advantage in winning algorithm responsible for both the encryption and decryption wars over enemies according to history and is also utilized as processes of a file being protected.
    [Show full text]
  • Certificate in E Certificate in E-Governance and Security Information System (CEGCS-04) Vernance and Cyber
    Certificate in e -Governance and Cyber Security Information System (CEGCS-04) Title Information System Adviso rs Mr. R. Thyagarajan, Head, Admn. & Finance and Acting Director, CEMCA Dr. Manas Ranjan Panigrahi, Program Officer(Education) , CEMCA Prof. Durgesh Pant, Director -SCS&IT, UOU Editor Er. Gopesh Pande, Network Engineer, Wipro Infotech, Mumbai Authors Block I> Unit I, Unit II, Unit III & Unit IV Er. Charanjeet Singh Chawla, Wing Commander, Indian Air Force, Ministry of Defence Block II> Unit I, Unit II, Unit III & Unit IV Er. Ashok Katariya, Group Captain, Indian Air Force, Ministry of Defence Block III> Unit I, Unit II, Unit III & Unit IV Er. Ashok Katariya, Group Captain, Indian Air Force, Ministry of Defence ISBN : 978 -93 -84813 -93 -2 Acknowledgement The University acknow ledges with thanks the expertixe and financial support provided by Commonwealth Educational Media Centre for Asia(CEMCA), New Delhi, for the preparation of this study material. Uttarakhand Open University, 2016 © Uttarak hand Open University, 2016. Information System is made available under a Creative Commons Attribution Share-Alike 4.0 Licence (international): http://creativecommons.org/licenses/by -sa/4.0/ It is attributed to the sources marked in the References, Article Sources and Contributors section. Published by: Uttarakhand Open University, Haldwani Expert Panel S. No. Name 1 Dr. Jeetendra Pande, School of Computer Science & IT, Uttarakhand Open University, Haldwani 2 Prof. Ashok Panjwani, Professor, MDI, Gurgoan 3 Group Captain Ashok Katariya, Ministry of Defense, New Delhi 4 Mr. Ashutosh Bahuguna, Scientist- CERT-In, Department Of Electronics & Information Technology, Government Of India 5 Mr. Sani Abhilash, Scientist- CERT-In, Department Of Electronics & Information Technology, Government Of India 6 Wing Commander C.S.
    [Show full text]
  • Computer and Data Security Class 4 ﺳﻜﻴﻨﺔ ﺣﺴﻦ هﺎﺷﻢ . د: أﺳﺘﺎذة اﻟﻤﺎدة
    Save from: www.uotechnology.edu.iq/dep‐cs Computer and Data security 4th Class أﺳﺘﺎذة اﻟﻤﺎدة: د. ﺳﻜﻴﻨﺔ ﺣﺴﻦ هﺎﺷﻢ Introduction to Data Security Basic Terminology Suppose that someone wants to send a message to a receiver, and wants to be sure that no-one else can read the message. However, there is the possibility that someone else opens the letter or hears the electronic communication. In cryptographic terminology, the message is called plaintext or cleartext. Encoding the contents of the message in such a way that hides its contents from outsiders is called encryption. The encrypted message is called the ciphertext. The process of retrieving the plaintext from the ciphertext is called decryption. Encryption and decryption usually make use of a key, and the coding method is such that decryption can be performed only by knowing the proper key. Cryptography is the art or science of keeping messages secret. Cryptanalysis is the art of breaking ciphers, i.e. retrieving the plaintext without knowing the proper key. People who do cryptography are cryptographers, and practitioners of cryptanalysis are cryptanalysts. Cryptography deals with all aspects of secure messaging, authentication, digital signatures, electronic money, and other applications. Cryptology is the branch of mathematics that studies the mathematical foundations of cryptographic methods. Basic Cryptographic Algorithms A method of encryption and decryption is called a cipher. Some cryptographic methods rely on the secrecy of the algorithms; such algorithms are only of historical interest and are not adequate for real-world needs. All modern algorithms 1 use a key to control encryption and decryption; a message can be decrypted only if the key matches the encryption key.
    [Show full text]
  • Book Cipher, Running Key Cipher, Vic Cipher and Secom Cipher
    BOOK CIPHER, RUNNING KEY CIPHER, VIC CIPHER AND SECOM CIPHER A book cipher is a cipher in which the key is some aspect of a book or other piece of text; books being common and widely available in modern times, users of book ciphers take the position that the details of the key is sufficiently well hidden from attackers in practice. This is in some ways an example of security by obscurity . It is typically essential that both correspondents not only have the same book, but the same edition .[1] Traditionally book ciphers work by replacing words in the plaintext of a message with the location of words from the book being used. In this mode, book ciphers are more properly called codes. This can have problems; if a word appears in the plaintext but not in the book, it cannot be encoded. An alternative approach which gets around this problem is to replace individual letters rather than words. One such method, used in the second Beale cipher , substitutes the first letter of a word in the book with that word's position. In this case, the book cipher is properly a cipher — specifically, a homophonic substitution cipher . However, if used often, this technique has the side effect of creating a larger ciphertext (typically 4 to 6 digits being required to encipher each letter or syllable) and increases the time and effort required to decode the message. Choosing the Key [] The main strength of a book cipher is the key. The sender and receiver of encoded messages can agree to use any book or other publication available to both of them as the key to their cipher.
    [Show full text]