General Procedure for Solution of Contact Problems Under Dynamic Normal and Tangential Loading Based on the Known Solution of Normal Contact Problem
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Forces Different Types of Forces
Forces and motion are a part of your everyday life for example pushing a trolley, a horse pulling a rope, speed and acceleration. Force and motion causes objects to move but also to stay still. Motion is simply a movement but needs a force to move. There are 2 types of forces, contact forces and act at a distance force. Forces Every day you are using forces. Force is basically push and pull. When you push and pull you are applying a force to an object. If you are Appling force to an object you are changing the objects motion. For an example when a ball is coming your way and then you push it away. The motion of the ball is changed because you applied a force. Different Types of Forces There are more forces than push or pull. Scientists group all these forces into two groups. The first group is contact forces, contact forces are forces when 2 objects are physically interacting with each other by touching. The second group is act at a distance force, act at a distance force is when 2 objects that are interacting with each other but not physically touching. Contact Forces There are different types of contact forces like normal Force, spring force, applied force and tension force. Normal force is when nothing is happening like a book lying on a table because gravity is pulling it down. Another contact force is spring force, spring force is created by a compressed or stretched spring that could push or pull. Applied force is when someone is applying a force to an object, for example a horse pulling a rope or a boy throwing a snow ball. -

Ground Reaction Force Prediction During Weighted Leg Press and Weighted Squat in a Flywheel Exercise Device
DEGREE PROJECT IN MEDICAL ENGINEERING, SECOND CYCLE, 30 CREDITS STOCKHOLM, SWEDEN 2017 Ground Reaction Force Prediction during Weighted Leg Press and Weighted Squat in a Flywheel Exercise Device Estimering av markreaktionskraften vid viktad benpress och viktad knäböj i ett svänghjulsbaserat träningsredskap TOBIAS MUNKHAMMAR KTH ROYAL INSTITUTE OF TECHNOLOGY SCHOOL OF TECHNOLOGY AND HEALTH Acknowledgement First of I would like to thank my supervisor, Maria J¨onsson,for guidance and encouragement during the whole project and Lena Norrbrand, who, together with Maria collected all experi- mental data used in this study. Furthermore, my thanks goes to Rodrigo Moreno, Jan H¨ornfeldt, Jonathan Munkhammar and Ola Eiken for proof-reading and general feedback on the report and Elena Gutierrez Farewik, for being a link towards the musculoskeletal software company whenever the licence struggled. Lastly, I would like to thank all people at the Department of Environmental Physiology, for making me feel welcome and showing interest in my work. Abstract When performing a biomechanical analysis of human movement, knowledge about the ground reaction force (GRF) is necessary to compute forces and moments within joints. This is important when analysing a movement and its effect on the human body. To obtain knowledge about the GRF, the gold standard is to use force plates which directly measure all three components of the GRF (mediolateral, anteroposterior and normal). However, force plates are heavy, clunky and expensive, setting constraints on possible experimental setups, which make it desirable to exclude them and instead use a predictive method to obtain the full GRF. Several predictive methods exist. The node model is a GRF predictive method included in a musculoskeletal modeling software. -

Physics 101 Today Chapter 5: Newton's Third
Physics 101 Today Chapter 5: Newton’s Third Law First, let’s clarify notion of a force : Previously defined force as a push or pull. Better to think of force as an interaction between two objects. You can’t push anything without it pushing back on you ! Whenever one object exerts a force on a second object, the second object exerts an equal and opposite force on the first. Newton’s 3 rd Law - often called “action-reaction ” Eg. Leaning against a wall. You push against the wall. The wall is also pushing on you, equally hard – normal/support force. Now place a piece of paper between the wall and hand. Push on it – it doesn’t accelerate must be zero net force. The wall is pushing equally as hard (normal force) on the paper in the opposite direction to your hand, resulting in zero Fnet . This is more evident when hold a balloon against the wall – it is squashed on both sides. Eg. You pull on a cart. It accelerates. The cart pulls back on you (you feel the rope get tighter). Can call your pull the “ action ” and cart’s pull the “ reaction ”. Or, the other way around. • Newton’s 3 rd law means that forces always come in action -reaction pairs . It doesn’t matter which is called the action and which is called the reaction. • Note: Action-reaction pairs never act on the same object Examples of action-reaction force pairs In fact it is the road’s push that makes the car go forward. Same when we walk – push back on floor, floor pushes us forward. -

The Amazing Normal Forces
THE AMAZING NORMAL FORCES Horia I. Petrache Department of Physics, Indiana University Purdue University Indianapolis Indianapolis, IN 46202 November 9, 2012 Abstract This manuscript is written for students in introductory physics classes to address some of the common difficulties and misconceptions of the normal force, especially the relationship between normal and friction forces. Accordingly, it is intentionally informal and conversational in tone to teach students how to build an intuition to complement mathematical formalism. This is accomplished by beginning with common and everyday experience and then guiding students toward two realizations: (i) That real objects are deformable even when deformations are not easily visible, and (ii) that the relation between friction and normal forces follows from the action-reaction principle. The traditional formulae under static and kinetic conditions are then analyzed to show that peculiarity of the normal-friction relationship follows readily from observations and knowledge of physics principles. 1 1. Normal forces: amazing or amusing? Learning about normal forces can be a life changing event. In introductory physics, we accept and embrace these totally mysterious things. Suddenly, normal forces become a convenient answer to everything: they hold objects on floors, on walls, in elevators and even on ceilings. They lift heavy weights on platforms, let footballs bounce, basketball players jump, and as if this was not enough, they even tell friction what to do. (Ah, the amazing friction forces – yet another amazing story! [1]) Life before physics becomes inexplicable. This article is about building an intuition about normal forces using the action-reaction law of mechanics and the fact that real objects are deformable. -
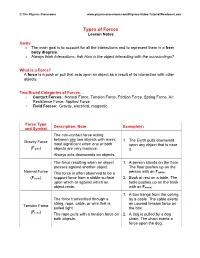
Types of Forces Lesson Notes
© The Physics Classroom www.physicsclassroom.com/Physics-Video-Tutorial/Newtons-Laws Types of Forces Lesson Notes Goals • The main goal is to account for all the interactions and to represent them in a free- body diagram. • Always think Interactions. Ask How is the object interacting with the surroundings? What is a Force? A force is a push or pull that acts upon an object as a result of its interaction with other objects. Two Broad Categories of Forces: • Contact Forces: Normal Force, Tension Force, Friction Force, Spring Force, Air Resistance Force, Applied Force • Field Forces: Gravity, electrical, magnetic Force Type Description, Note Example(s) and Symbol The non-contact force acting between any two objects with mass; Gravity Force 1. The Earth pulls downward most significant when one or both upon any object that is near (Fgrav) objects are very massive. it. Always acts downwards on objects. The force resulting when an object 1. A person stands on the floor. presses against another object. The floor pushes up on the Normal Force This force is often observed to be a person with an Fnorm. (Fnorm) support force from a stable surface 2. Book at rest on a table. The upon which or against which an table pushes up on the book object rests. with an Fnorm. 1. A box hangs from the ceiling The force transmitted through a by a cable. The cable exerts string, rope, cable, or wire that is an upward tension force on Tension Force pulled tight. the box. (F ) tens The rope pulls with a tension force on 2. -

Weight and the Normal Force CRHS-South
Lyzinski Physics Weight and the Normal Force CRHS-South Force due to gravity and the normal force Force due to gravity: A field force (a vector quantity) that always is directed towards the center of the earth. Weight: The magnitude of the Force due to gravity 2 2 Fg W mg gearth = 9.8 m/s gmoon = 1.6 m/s Mass vs. weight Mass: A measure of an objects inertia Weight: Decreases as you move away from the (its tendency to resist a change in center of the earth. NOT an inherent its motion). Inherent property of property of an object an object. Normal Force: A “reactionary” contact force exerted on one object by another in a direction perpendicular () to the surface of contact. 1) Compare the weight of a 60 kg person on the earth with the weight of the same person on the moon. Then, describe a quick (but very costly) way for dieters at NASA to lose weight. 2) A bully is pushing a boy against a locker as shown with a force of 500N. The angle between his arms and the ground is 40o. Draw a free-body diagram of the boy and then find the normal force between the boy and the wall. 3) A 200 kg block, on a VERY rough surface, is being pulled/pushed by two people, one on each end. The first person is pulling with a force of 20 N at an angle of 40o above the ground, while the other person is pushing with a 30 N force at an angle of 50o above the ground. -

3-6 Exploring Forces and Free-Body Diagrams a Force Is Simply a Push Or a Pull
Answer to Essential Question 3.5: Even though the Sun is enormous compared to the Earth, Newton’s third law tells us that the force the Sun exerts on the Earth is equal in magnitude, and opposite in direction, to the force the Earth exerts on the Sun. 3-6 Exploring Forces and Free-Body Diagrams A force is simply a push or a pull. A force is a vector, so it has a direction. Also, a force represents an interaction between objects. Let’s build on these facts and learn more about forces. EXPLORATION 3.6A – The normal force Step 1 - Sketch free-body diagrams for the following situations: (a) a book rests on a table; (b) you exert a downward force on the book as it sits on the table; (c) you tie a helium-filled balloon to the book, which remains on the table. The diagrams are shown in Figure 3.13. In (a), the normal force applied by the table on the book has to balance the force of gravity acting on the book. If you push down on the book, the normal force increases – it has to balance the force of gravity as well as the force you exert. Tying a helium balloon to the book reduces the normal force because the normal force and the tension in the string combine to balance the force of gravity. The normal force depends on the situation – the magnitude of the normal force is whatever is Figure 3.13: The upward normal force necessary to prevent the book from falling through the table. -

8.01 Classical Mechanics Chapter
8.3 Constraint Forces Knowledge of all the external and internal forces acting on each of the objects in a system and applying Newton’s Second Law to each of the objects determine a set of equations of motion. These equations of motion are not necessarily independent due to the fact that the motion of the objects may be limited by equations of constraint. In addition there are forces of constraint that are determined by their effect on the motion of the objects and are not known beforehand or describable by some force law. For example: an object sliding down an inclined plane is constrained to move along the surface of the inclined plane (Figure 8.6a) and the surface exerts a contact force on the object; an object that slides down the surface of a sphere until it falls off experiences a contact force until it loses contact with the surface (Figure 8.6b); gas particles in a sealed vessel are constrained to remain inside the vessel and therefore the wall must exert force on the gas molecules to keep them inside the vessel (8.6c); and a bead constrained to slide outward along a rotating rod is acting on by time dependent forces of the rod on the bead (Figure 8.6d). We shall develop methods to determine these constraint forces although there are many examples in which the constraint forces cannot be determined.. inclined plane (a) (b) ' bead rotating rod (c) (d) ' 8-1 Figure 8.6 Constrained motions: (a) particle sliding down inclined plane, (b) particles sliding down surface of sphere, (c) gas molecules in a sealed vessel, and (d) bead sliding on a rotating rod 8.3.1 Contact Forces Pushing, lifting and pulling are contact forces that we experience in the everyday world. -

Forces Different Forces
Forces and motion are very important in everyday life. Forces and motion make things move but also stay where they are. Motion simply is just movement but it needs a force to make it movemove.. A force is a push or pull on an object, which causes things to move or slow down. There are two types of forces. Forces Force is just a fancy word for pushing or pulling. If you push or pull you are applying a force. For example: if you openopen a door you are applying a force. Forces mamakeke thing move or change their direction. Different forces There are two types of forces, contact forces and at a distance forcesforces.. Contact forces involve pushpush,,,, pull and friction. A contact force is when two interacting objects are physically touching, for example: when you are throwing a baballll you are using a contact force. At a distance force is when two interacting objects are not touching, for example: the moon and the Earth’s seas. At a distance forces encompasses gravity and magnetism. Contact forceforcessss There are four types of contact forces Normal force, applied forceforce,, tension force and spring force. A normal force is when nothing is happening. A book resting on a table has gravity pulling it to the ground. There are oppositing forces acting on the bookbook caused by the table. An applieappliedd force is a force applied to an object to make it move, for example: a person moving furniture, the person is applying a force to make the furniture move. A tension force is a force applied to a cable or wire anchored on opposite ends to oppositing walls or objects. -

Chapter 1: Forces 1) the Coefficient of Static Friction Between a Tennis
Chapter 1: Forces 1) The coefficient of static friction between a tennis player's hand and her racket is 0.45. How hard must she squeeze the racket if she wants to exert a force of 200 N along its longitudinal axis? F = μN F = 200N μ = 0.45 200N = 0.45(Normal Force) Normal force = 200N/0.45 = 444N 2) The coefficient of static friction between the sole of an athletic shoe and the basketball court floor is 0.67. Tyler wears these shoes when he plays basketball. If Tyler exerts a normal contact force of 1400 N when he pushes off the floor to run down the court, how large is the friction force exerted by Tyler’s shoes on the floor? Frictional force = F Coefficient of static friction = 0.67 Normal force = 1400N F = μN F = 0.67 (1400N) = 938N 3) A sprinter is just coming out of the starting block, and only one foot is touching the block. The sprinter pushes back (horizontally) against the block with a force of 500 N and down (vertically) against the ground with a force of 800 N. What is the resultant of these forces? Magnitude Pythagorean Theorum a2 + b2 = c2 c = sqrt(a2 + b2) Resultant = sqrt(500N2 + 800N2) = 943N Direction tan θ = opp/adj θ = tan-1 (opp/adj) -1 θ = tan (800N/500N) = 58° below horizontal 4) A 60-kg skier is in a tuck and moving straight down a 30 slope. Air resistance pushes backward on the skier with a force of 10 N (this force acts in a direction upward and parallel to the 30 slope). -

Normal Force and Friction
PHYSICS 149: Lecture 6 • Chapter 2 – 2.7 Contact Forces: Normal Force and Friction – 2.8 Tension Lecture 6 Purdue University, Physics 149 1 ILQ 1 If the distance to the moon were halved, then the force of attraction between the earth and moon would be: A) quartered (.25 x) B) halved (. 5 x) C) doubled (2 x) D) quadrupled (4 x) Lecture 6 Purdue University, Physics 149 2 Normal (= Perpendicular) Force • The normal force is a contact force perpendicular to the contact surfaces that prevents two objects from passing through one another. • Normal force is a vector. – Direction: always perpendicular to the “contact surface” (()rather than the horizon) – Magnitude: depends on the weight of the object (see different cases on next pages) • Type: contact force (not long-range force) • Normal force is usually denoted by N. Lecture 6 Purdue University, Physics 149 3 Normal Force • Symbol for FBD: N • Type: Contact force • Direction is normal (perpendicular) to surface • This i s th e norma l componen t for th e con tact force between two (planar) surfaces Lecture 6 Purdue University, Physics 149 4 What Causes Normal Force? • Atoms inside solid objects are inter-connected by molecular bonds which act like springs. • When yypou place an obj ect on to p of a table, the table deforms slightly. This bend is usually not visible to the eye. • The "springs" holding the atoms ithtblin the table compress or s tthtretch exerting a force on the object on the table. Lecture 6 Purdue University, Physics 149 5 Normal Force: Case 1 • If the table’s surface (contact surface) is horizontal, – Direction of the normal force is perpendicular to the “contact surface.” In this case, vertically upward. -

Examples of Forces
Examples of Forces • A force is just a push or pull. Examples: – an object’s weight – tension in a rope – a left hook to the schnozola – friction – attraction between an electron and proton • Bodies don’t have to be in contact to exert forces on each other, e.g., gravity. Newton’s Laws of Motion 1. Inertia: “An object in motion tends to stay in motion. An object at rest tends to stay at rest.” 2. Fnet = ma 3. Action – Reaction: “For every action there is an equal but opposite reaction.” nd 2 Law: Fnet = m a • The acceleration an object undergoes is directly proportion to the net force acting on it. • Mass is the constant of proportionality. • For a given mass, if Fnet doubles, triples, etc. in size, so does a. • For a given Fnet if m doubles, a is cut in half. • Fnet and a are vectors; m is a scalar. • Fnet and a always point in the same direction. • The 1st law is really a special case of the 2nd law (if net force is zero, so is acceleration). What is Net Force? F 1 When more than one force acts on a body, F2 the net force F3 (resultant force) is the vector combination of all the forces, i.e., the “net effect.” Fnet Net Force & the 2nd Law For a while, we’ll only deal with forces that are horizontal or vertical. When forces act in the same line, we can just add or subtract their magnitudes to find the net force. 15 N 32 N 2 kg 10 N Fnet = 27 N to the right 2 a = 13.5 m/s Units Fnet = m a 1 N = 1 kg m/s2 The SI unit of force is the Newton.