An Adaptive Multilayer Model for Density-Layered Shallow Water Flows
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Understanding Eddy Field in the Arctic Ocean from High-Resolution Satellite Observations Igor Kozlov1, A
Abstract ID: 21849 Understanding eddy field in the Arctic Ocean from high-resolution satellite observations Igor Kozlov1, A. Artamonova1, L. Petrenko1, E. Plotnikov1, G. Manucharyan2, A. Kubryakov1 1Marine Hydrophysical Institute of RAS, Russia; 2School of Oceanography, University of Washington, USA Highlights: - Eddies are ubiquitous in the Arctic Ocean even in the presence of sea ice; - Eddies range in size between 0.5 and 100 km and their orbital velocities can reach up to 0.75 m/s. - High-resolution SAR data resolve complex MIZ dynamics down to submesoscales [O(1 km)]. Fig 1. Eddy detection Fig 2. Spatial statistics Fig 3. Dynamics EGU2020 OS1.11: Changes in the Arctic Ocean, sea ice and subarctic seas systems: Observations, Models and Perspectives 1 Abstract ID: 21849 Motivation • The Arctic Ocean is a host to major ocean circulation systems, many of which generate eddies transporting water masses and tracers over long distances from their formation sites. • Comprehensive observations of eddy characteristics are currently not available and are limited to spatially and temporally sparse in situ observations. • Relatively small Rossby radii of just 2-10 km in the Arctic Ocean (Nurser and Bacon, 2014) also mean that most of the state-of-art hydrodynamic models are not eddy-resolving • The aim of this study is therefore to fill existing gaps in eddy observations in the Arctic Ocean. • To address it, we use high-resolution spaceborne SAR measurements to detect eddies over the ice-free regions and in the marginal ice zones (MIZ). EGU20 -OS1.11 – Kozlov et al., Understanding eddy field in the Arctic Ocean from high-resolution satellite observations 2 Abstract ID: 21849 Methods • We use multi-mission high-resolution spaceborne synthetic aperture radar (SAR) data to detect eddies over open ocean and marginal ice zones (MIZ) of Fram Strait and Beaufort Gyre regions. -

The General Circulation of the Atmosphere and Climate Change
12.812: THE GENERAL CIRCULATION OF THE ATMOSPHERE AND CLIMATE CHANGE Paul O'Gorman April 9, 2010 Contents 1 Introduction 7 1.1 Lorenz's view . 7 1.2 The general circulation: 1735 (Hadley) . 7 1.3 The general circulation: 1857 (Thompson) . 7 1.4 The general circulation: 1980-2001 (ERA40) . 7 1.5 The general circulation: recent trends (1980-2005) . 8 1.6 Course aim . 8 2 Some mathematical machinery 9 2.1 Transient and Stationary eddies . 9 2.2 The Dynamical Equations . 12 2.2.1 Coordinates . 12 2.2.2 Continuity equation . 12 2.2.3 Momentum equations (in p coordinates) . 13 2.2.4 Thermodynamic equation . 14 2.2.5 Water vapor . 14 1 Contents 3 Observed mean state of the atmosphere 15 3.1 Mass . 15 3.1.1 Geopotential height at 1000 hPa . 15 3.1.2 Zonal mean SLP . 17 3.1.3 Seasonal cycle of mass . 17 3.2 Thermal structure . 18 3.2.1 Insolation: daily-mean and TOA . 18 3.2.2 Surface air temperature . 18 3.2.3 Latitude-σ plots of temperature . 18 3.2.4 Potential temperature . 21 3.2.5 Static stability . 21 3.2.6 Effects of moisture . 24 3.2.7 Moist static stability . 24 3.2.8 Meridional temperature gradient . 25 3.2.9 Temperature variability . 26 3.2.10 Theories for the thermal structure . 26 3.3 Mean state of the circulation . 26 3.3.1 Surface winds and geopotential height . 27 3.3.2 Upper-level flow . 27 3.3.3 200 hPa u (CDC) . -

Physical Oceanography and Circulation in the Gulf of Mexico
Physical Oceanography and Circulation in the Gulf of Mexico Ruoying He Dept. of Marine, Earth & Atmospheric Sciences Ocean Carbon and Biogeochemistry Scoping Workshop on Terrestrial and Coastal Carbon Fluxes in the Gulf of Mexico St. Petersburg, FL May 6-8, 2008 Adopted from Oey et al. (2005) Adopted from Morey et al. (2005) Averaged field of wind stress for the GOM. [adapted from Gutierrez de Velasco and Winant, 1996] Surface wind Monthly variability Spring transition vs Fall Transition Adopted from Morey et al. (2005) Outline 1. General circulation in the GOM 1.1. The loop current and Eddy Shedding 1.2. Upstream conditions 1.3. Anticyclonic flow in the central and northwestern Gulf 1.4. Cyclonic flow in the Bay of Campeche 1.5. Deep circulation in the Gulf 2. Coastal circulation 2.1. Coastal Circulation in the Eastern Gulf 2.2. Coastal Circulation in the Northern Gulf 2.3. Coastal Circulation in the Western Gulf 1. General Circulation in the GOM 1.1. The Loop Current (LC) and Eddy Shedding Eddy LC Summary statistics for the Loop Current metrics computed from the January1, 1993 through July 1, 2004 altimetric time series Leben (2005) A compilation of the 31-yr Record (July 1973 – June 2004) of LC separation event. The separation intervals vary From a few weeks up to ~ 18 Months. Separation intervals tend to Cluster near 4.5-7 and 11.5, And 17-18.5 months, perhaps Suggesting the possibility of ~ a 6 month duration between each cluster. Leben (2005); Schmitz et al. (2005) Sturges and Leben (1999) The question of why the LC and the shedding process behave in such a semi-erratic manner is a bit of a mystery • Hurlburt and Thompson (1980) found erratic eddy shedding intervals in the lowest eddy viscosity run in a sequence of numerical experiment. -

Pressure-Gradient Forcing Methods for Large-Eddy Simulations of Flows in the Lower Atmospheric Boundary Layer
atmosphere Article Pressure-Gradient Forcing Methods for Large-Eddy Simulations of Flows in the Lower Atmospheric Boundary Layer François Pimont 1,* , Jean-Luc Dupuy 1 , Rodman R. Linn 2, Jeremy A. Sauer 3 and Domingo Muñoz-Esparza 3 1 Department of Forest, Grassland and Freshwater Ecology, Unité de Recherche des Forets Méditerranéennes (URFM), French National Institute for Agriculture, Food, and Environment (INRAE), CEDEX 9, 84914 Avignon, France; [email protected] 2 Earth and Environmental Sciences Division, Los Alamos National Lab, Los Alamos, NM 87545, USA; [email protected] 3 Research Applications Laboratory, National Center for Atmospheric Research, Boulder, CO 80301, USA; [email protected] (J.A.S.); [email protected] (D.M.-E.) * Correspondence: [email protected]; Tel.: +33-432-722-947 Received: 26 October 2020; Accepted: 9 December 2020; Published: 11 December 2020 Abstract: Turbulent flows over forest canopies have been successfully modeled using Large-Eddy Simulations (LES). Simulated winds result from the balance between a simplified pressure gradient forcing (e.g., a constant pressure-gradient or a canonical Ekman balance) and the dissipation of momentum, due to vegetation drag. Little attention has been paid to the impacts of these forcing methods on flow features, despite practical challenges and unrealistic features, such as establishing stationary velocity or streak locking. This study presents a technique for capturing the effects of a pressure-gradient force (PGF), associated with atmospheric patterns much larger than the computational domain for idealized simulations of near-surface phenomena. Four variants of this new PGF are compared to existing forcings, for turbulence statistics, spectra, and temporal averages of flow fields. -

SWASHES: a Compilation of Shallow Water Analytic Solutions For
SWASHES: a compilation of Shallow Water Analytic Solutions for Hydraulic and Environmental Studies O. Delestre∗,‡,,† C. Lucas‡, P.-A. Ksinant‡,§, F. Darboux§, C. Laguerre‡, T.N.T. Vo‡,¶, F. James‡ and S. Cordier‡ January 22, 2016 Abstract Numerous codes are being developed to solve Shallow Water equa- tions. Because there are used in hydraulic and environmental studies, their capability to simulate properly flow dynamics is critical to guaran- tee infrastructure and human safety. While validating these codes is an important issue, code validations are currently restricted because analytic solutions to the Shallow Water equations are rare and have been published on an individual basis over a period of more than five decades. This article aims at making analytic solutions to the Shallow Water equations easily available to code developers and users. It compiles a significant number of analytic solutions to the Shallow Water equations that are currently scat- tered through the literature of various scientific disciplines. The analytic solutions are described in a unified formalism to make a consistent set of test cases. These analytic solutions encompass a wide variety of flow conditions (supercritical, subcritical, shock, etc.), in 1 or 2 space dimen- sions, with or without rain and soil friction, for transitory flow or steady state. The corresponding source codes are made available to the commu- nity (http://www.univ-orleans.fr/mapmo/soft/SWASHES), so that users of Shallow Water-based models can easily find an adaptable benchmark library to validate their numerical methods. Keywords Shallow-Water equation; Analytic solutions; Benchmarking; Vali- dation of numerical methods; Steady-state flow; Transitory flow; Source terms arXiv:1110.0288v7 [math.NA] 21 Jan 2016 ∗Corresponding author: [email protected], presently at: Laboratoire de Math´ematiques J.A. -

Lecture 7: Atmospheric General Circulation
The climatological mean circulation Deviations from the climatological mean Synthesis: momentum and the jets Lecture 7: Atmospheric General Circulation Jonathon S. Wright [email protected] 11 April 2017 The climatological mean circulation Deviations from the climatological mean Synthesis: momentum and the jets The climatological mean circulation Zonal mean energy transport Zonal mean energy budget of the atmosphere The climatological mean and seasonal cycle Deviations from the climatological mean Transient and quasi-stationary eddies Eddy fluxes of heat, momentum, and moisture Eddies in the atmospheric circulation Synthesis: momentum and the jets Vorticity and Rossby waves Momentum fluxes Isentropic overturning circulation The climatological mean circulation Zonal mean energy transport Deviations from the climatological mean Zonal mean energy budget of the atmosphere Synthesis: momentum and the jets The climatological mean and seasonal cycle 400 Outgoing longwave radiation 350 net energy loss in Incoming solar radiation ] 2 − 300 the extratropics m 250 W [ x 200 u l f y 150 net energy gain g r e n 100 E in the tropics 50 0 90°S 60°S 30°S 0° 30°N 60°N 90°N 6 4 2 0 2 Energy flux [PW] 4 JRA-55 6 90°S 60°S 30°S 0° 30°N 60°N 90°N data from JRA-55 The climatological mean circulation Zonal mean energy transport Deviations from the climatological mean Zonal mean energy budget of the atmosphere Synthesis: momentum and the jets The climatological mean and seasonal cycle 400 Outgoing longwave radiation 350 Incoming solar radiation ] 2 − 300 -

Upwelling and Isolation in Oxygen-Depleted
Biogeosciences Discuss., doi:10.5194/bg-2016-34, 2016 Manuscript under review for journal Biogeosciences Published: 11 March 2016 c Author(s) 2016. CC-BY 3.0 License. Upwelling and isolation in oxygen-depleted anticyclonic modewater eddies and implications for nitrate cycling Johannes Karstensen1, Florian Schütte1, Alice Pietri2, Gerd Krahmann1, Björn Fiedler1, Damian Grundle1, Helena Hauss1, Arne Körtzinger1,3, Carolin R. Löscher1, Pierre Testor2, Nuno Viera4, Martin 5 Visbeck1,3 1GEOMAR, Helmholtz Zentrum für Ozeanforschung Kiel, Düsternbrooker Weg 20, 24105 Kiel, Germany 2LOCEAN, UMPC; Paris, France 3Kiel University, Kiel Germany 4Instituto Nacional de Desenvolvimento das Pescas (INDP), Cova de Inglesa, Mindelo, São Vicente, Cabo Verde 10 Correspondence to: Johannes Karstensen ([email protected]) Abstract. The physical (temperature, salinity, velocity) and biogeochemical (oxygen, nitrate) structure of an oxygen depleted coherent, baroclinic, anticyclonic mode-water eddy (ACME) is investigated using high-resolution autonomous glider and ship data. A distinct core with a diameter of about 70 km is found in the eddy, extending from about 60 to 200 m depth and. The core is occupied by fresh and 15 cold water with low oxygen and high nitrate concentrations, and bordered by local maxima in buoyancy frequency. Velocity and property gradient sections show vertical layering at the flanks and underneath the eddy characteristic for vertical propagation (to several hundred-meters depth) of near inertial internal waves (NIW) and confirmed by direct current measurements. A narrow region exists at the outer edge of the eddy where NIW can propagate downward. NIW phase speed and mean flow are of 20 similar magnitude and critical layer formation is expected to occur. -

The Atmospheric General Circulation and Its Variability Dennis L
The Atmospheric General Circulation and its Variability Dennis L. Hartmann Department of Atmospheric Sciences, University of Washington, Seattle, Washington USA Abstract Progress in understanding the general circulation of the atmosphere during the past 25 years is reviewed. The relationships of eddy generation, propagation and dissipation to eddy momentum fluxes and mean zonal winds are now sufficiently understood that intuitive reasoning about momentum based on firm theoretical foundations is possible. Variability in the zonal-flow can now be understood as a process of eddy, zonal-flow interaction. The interaction of tropical overturning circulations driven by latent heating with extratropical wave-driven jets is becoming a fruitful and interesting area of study. Gravity waves have emerged as an important factor in the momentum budget of the general circulation and are now included in weather and climate models in parameterized form. Stationary planetary waves can largely be explained with linear theory. 1. Introduction: I attempt here to give a summary of progress in understanding the general circulation of the atmosphere in the past 25 years, in celebration of the 125th anniversary of the Meteorological Society of Japan. This is a daunting task, especially within the confines of an article of reasonable length. I will therefore concentrate on a few areas that seem most interesting and important to me and with which I am relatively familiar. I will not attempt to give a full list of references, but will attempt to pick out a few important early references and some more recent references. Interested readers can use these data points to fill in the intervening developments. -
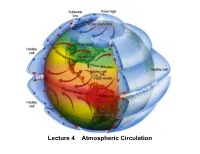
Lecture 4 Atmospheric Circulation
Lecture 4 Atmospheric Circulation THE ZONALLY- AVERAGED CIRCULATION part I, zonal winds Schematic of wind intensity in the west to east direction near the Earth’s Surface Winds blowing from the west are called westerlies, Winds blowing from the east are called easterlies. POLAR At the Earth’s EASTERLIES surface, winds are primarily from the WESTERLIES west in mid-latitudes and from the east in low and high TRADES latitudes. Schematic showing outstanding features of the zonally averaged zonal wind distribution ZONAL WIND 70 Km E W POLAR-NIGHT JET SUMMER JET (~80 - 100 m/s) (~50 m/s) 50 Km 0 0 30 30 Km 0 10 Km W W SUBTROPICA L JET (~35 m/s) Summer Equator Winter Pole Pole THE ZONALLY- AVERAGED CIRCULATION part II, meridional winds Annual-average atmospheric mass circulation in the latitude pressure plane (meridional plane). The arrows depict the direction of air movement in the meridional plane. The contour interval is 2x1010 Kg/sec - this is the amount of mass that is circulating between every two contours. The total amount of mass circulating around each "cell" is given by the largest value in that cell. Data based on the NCEP-NCAR reanalysis project 1958-1998. The Hadley Cells DJF and JJA meridional overturning circulation. Units are 1010 kg s-1 Hadley circulation and heat budget in subtropics Radiation solar down infrared up Latent heating in convective rain Dynamical warming by subsidence Dynamical Heat transport cooling by by transients advection Evaporation Moisture Moisture transport transport warm Ocean heat transport Three-Cell Circulation Model The cells tops are around the tropopause NORTH-SOUTH VERTICAL SECTION TROUGH TROPOSPHERE Here we point out an apparent contradiction: The meridional overturning cells weaken in midlatitudes, but the energy transport deduced from radiative balance peaks. -

Large Eddy Simulation Modeling of Tsunami-Like Solitary Wave Processes Over Fringing Reefs
Nat. Hazards Earth Syst. Sci., 19, 1281–1295, 2019 https://doi.org/10.5194/nhess-19-1281-2019 © Author(s) 2019. This work is distributed under the Creative Commons Attribution 4.0 License. Large eddy simulation modeling of tsunami-like solitary wave processes over fringing reefs Yu Yao1,4, Tiancheng He1, Zhengzhi Deng2, Long Chen1,3, and Huiqun Guo1 1School of Hydraulic Engineering, Changsha University of Science and Technology, Changsha, Hunan 410114, China 2Ocean College, Zhejiang University, Zhoushan, Zhejiang 316021, China 3Key Laboratory of Water-Sediment Sciences and Water Disaster Prevention of Hunan Province, Changsha 410114, China 4Key Laboratory of Coastal Disasters and Defense of Ministry of Education, Nanjing, Jiangsu 210098, China Correspondence: Zhengzhi Deng ([email protected]) Received: 10 December 2018 – Discussion started: 21 January 2019 Accepted: 10 June 2019 – Published: 28 June 2019 Abstract. Many low-lying tropical and subtropical reef- the beach, overtop or ruin the coastal structures, and inundate fringed coasts are vulnerable to inundation during tsunami the coastal towns and villages (Yao et al., 2015). Some tropic events. Hence accurate prediction of tsunami wave transfor- and subtropical coastal areas vulnerable to tsunami hazards mation and run-up over such reefs is a primary concern in the are surrounded by coral reefs, especially those in the Pacific coastal management of hazard mitigation. To overcome the and Indian oceans. Among various coral reefs, fringing reefs deficiencies of using depth-integrated models in modeling are the most common type. A typical cross-shore fringing tsunami-like solitary waves interacting with fringing reefs, reef profile can be characterized by a steep offshore fore-reef a three-dimensional (3-D) numerical wave tank based on the slope and an inshore shallow reef flat (Gourlay, 1996). -

Filaments, Fronts and Eddies in the Cabo Frio Coastal Upwelling System, Brazil
fluids Article Filaments, Fronts and Eddies in the Cabo Frio Coastal Upwelling System, Brazil Paulo H. R. Calil 1,* , Nobuhiro Suzuki 1 , Burkard Baschek 1 and Ilson C. A. da Silveira 2 1 Institute of Coastal Ocean Dynamics, Helmholtz-Zentrum Geesthacht, 21502 Geesthacht, Germany; [email protected] (N.S.); [email protected] (B.B.) 2 Instituto Oceanográfico, Universidade de São Paulo, São Paulo 05508-120, Brazil; [email protected] * Correspondence: [email protected] Abstract: We investigate the dynamics of meso- and submesoscale features of the northern South Brazil Bight shelf region with a 500-m horizontal resolution regional model. We focus on the Cabo Frio upwelling center, where nutrient-rich, coastal waters are transported into the mid- and outer shelf, because of its importance for local and remote productivity. The Cabo Frio upwelling center undergoes an upwelling phase, from late September to March, and a relaxation phase, from April to early September. During the upwelling phase, an intense front around 200 km long and 20 km wide with horizontal temperature gradients as large as 8 °C over less than 10 km develops. A surface- 1 1 intensified frontal jet of 0.7 ms− in the upper 20 m and velocities of around 0.3 ms− reaching down to 65 m depth makes this front a preferential cross-shelf transport pathway. Large vertical mixing and vertical velocities are observed within the frontal region. The front is associated with strong cyclonic vorticity and strong variance in relative vorticity, frequently with O(1) Rossby numbers. The dynamical balance within the front is between the pressure gradient, Coriolis and vertical mixing terms, which are induced both by the winds, during the upwelling season, and by the geostrophic frontal jet. -

The Shallow-Water Equations
Lecture 8: The Shallow-Water Equations Lecturer: Harvey Segur. Write-up: Hiroki Yamamoto June 18, 2009 1 Introduction The shallow-water equations describe a thin layer of fluid of constant density in hydrostatic balance, bounded from below by the bottom topography and from above by a free surface. They exhibit a rich variety of features, because they have infinitely many conservation laws. The propagation of a tsunami can be described accurately by the shallow-water equations until the wave approaches the shore. Near shore, a more complicated model is required, as discussed in Lecture 21. 2 Derivation of shallow-water equations To derive the shallow-water equations, we start with Euler’s equations without surface tension, Dη ∂η free surface condition : p = 0, = + v η = w, on z = η(x, y, t) (1) Dt ∂t · ∇ Du 1 momentum equation : + p + gzˆ = 0, (2) Dt ρ∇ continuity equation : u = 0, (3) ∇ · bottom boundary condition : u (z + h(x, y)) = 0, on z = h(x, y). (4) · ∇ − Here, p is the pressure, η the vertical displacement of free surface, u = (u, v, w) the three- dimensional velocity, ρ the density, g the acceleration due to gravity, and h(x, y) the bottom topography (Fig. 1). For the first step of the derivation of the shallow-water equations, we consider the global 71 Figure 1: Schematic illustration of the Euler’s system. mass conservation. We integrate the continuity equation (3) vertically as follows, η 0 = [ u]dz, (5) Z−h ∇ · η ∂u ∂v ∂w = + + dz, (6) Z−h ∂x ∂y ∂z ∂ η ∂η ∂( h) = udz u z=η + u z=−h − , ∂x Z−h − | ∂x | ∂x ∂ η ∂η ∂( h) + vdz v z=η + v z=−h − , ∂y Z−h − | ∂y | ∂y +w z=η w z=−h, (7) | − | ∂ η ∂η ∂ η ∂η = udz u z=η + vdz v z=η + w z=η.