Book of Abstracts
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

History and Challenges for the Future
The TSU and VIAM Jubilees: History and Challenges for the Future 2018 was marked with three Jubilees. Centenary of declaration of independence of the first Georgian Republic. Centenary of the I. Javakhishvili Tbilisi State Uni- versity (TSU), the eldest university in the Caucasus, and 50th anniversary of the I.Vekua Institute of Applied Mathematics (VIAM) which was founded at the Uni- versity after 50 years of foundation of the University and it is an only Institute which has been existing permanently for 50 years at the University. By the time of the establishment of Tbilisi State University only the faculty of philosophy with departments of Humanities, Mathematics, and Natural Sciences was opened in 1918. The faculty had 369 students, 7 Professors, 5 Deputy Profes- sors, 2 supervisor-scientists and 3 lecturers. Nowadays, 100 years later, Tbilisi State University is a top ranked institution among 2% of the top universities of the world (The U.S. News &World Report) and it owns 13 educational buildings (two of them have the status of historical heritage). Presently 67 undergraduate, 95 postgraduate and 51 Doctoral Degree Programs are implemented at 7 faculties of TSU (Faculty of Exact and Natural Sciences, Faculty of Economics and Business, Faculty of Law, Faculty of Social and Political Sciences, Faculty of Humanities, Faculty of Psychology and Educational Sciences, Faculty of Medicine). Besides, 19 vocational and 3 one-step educational programs are offered (at the Faculty of Medicine). In addition, the university provides training program for teachers as well as Georgian language preparation educational program for ethnic Azeri, Armenian and Abkhazian students. -

Energy Policy Review: Georgia 2020
Georgia 2020 Energy Policy Review Georgia 2020 Energy Policy Review INTERNATIONAL ENERGY AGENCY The IEA examines IEA member IEA association the full spectrum countries: countries: of energy issues including oil, gas Australia Brazil and coal supply and Austria China demand, renewable Belgium India energy technologies, Canada Indonesia electricity markets, Czech Republic Morocco energy efficiency, Denmark Singapore access to energy, Estonia South Africa demand side Finland Thailand management and France much more. Through Germany its work, the IEA Greece advocates policies Hungary that will enhance Ireland the reliability, Italy affordability and Japan sustainability of Korea energy in its 30 Luxembourg member countries, Mexico 8 association Netherlands countries and New Zealand beyond. Norway Poland Portugal Slovak Republic Spain Sweden Switzerland Turkey United Kingdom United States The European Commission also participates in the work of the IEA Please note that this publication is subject to specific restrictions that limit its use and distribution. The terms and conditions are available online at www.iea.org/t&c/ Source: IEA. All rights reserved. International Energy Agency Website: www.iea.org Foreword The International Energy Agency (IEA) has been conducting in-depth peer reviews of energy policies of its member countries – and of other countries – since 1976, and it recently modernised these reviews to focus on some of the countries’ key energy transition and security challenges. As the IEA has opened its doors to emerging economies, in-depth reviews have come to play an increasingly prominent role in bilateral collaborations. Georgia is one of the focus countries of the EU4Energy programme, which is implemented FOREWORD by the IEA and the European Union, along with the Energy Community and the Energy Charter, and which includes Armenia, Azerbaijan, Belarus, Georgia, Kazakhstan, Kyrgyzstan, Moldova, Tajikistan, Turkmenistan, Ukraine and Uzbekistan. -

Temur Chilachava 1. Education 2. Degree, Position, Publications
CURRICULUM VITAE (CV) Temur Chilachava Date of Birth: 05. 01. 1959 Work Place: Sokhumi State University Head of the department of applied mathematics Doctor of physical and mathematical sciences, Professor Address: 61 Politkovskaia str., 0186, Tbilisi, Georgia Tel: Web: www.sou.edu.ge Residence: Kvishkheti str., Tbilisi, Georgia Tel: +995 599809058 Email : [email protected] 1. Education 1. Date 1975 – 1980 Institution M. V. Lomonosov Moscow State University, mechanical- mathematical faculty Specialty mechanics Diploma № Г- I № 342845 (with honors) Degree qualification of "mechanics" 2. Degree, Position, Publications, Participations in Conference Degree PHD of Mathematical and Physical Sciences, Diploma FM № 022460, 1985, 3 April, Moscow Degree Doctor of Mathematical and Physical Sciences, Diploma № 000786, “Mathematical modeling, numerical methods, complexes of programs”, 05.13.18, 1999, February, Tbilisi Scientific and pedagogical Professor of mathematical physics (01.01.03), the certificate № 0000207, rank 2000, on March 20, (Tbilisi, TSU) 1 Position Professor, head of the department of applied mathematics Sokhumi State University Publications 140 (scientific articles, books, proceedings and theses of conferences) Participations in Conference 48 (74 reports) 3. Work Experience 1. Date 1985 - 1. 04. 1989 Institution Abkhazian state university Position Teacher (PHD of Mathematical and Physical Sciences) algebras, geometry; mathematical analysis departaments 2. Date 14.05. 1989 - 2000 Institution Sokhumi branch of the Tbilisi state university of Ivane Javakhishvili Position the associated professor, head of the department of applied mathematics Date 20.12. 1993 – 25.04.2005 Institution Sokhumi branch of the Tbilisi State University of Ivane Javakhishvili Position Vice-rector 4. Date 2000 - 2008 Institution Sokhumi branch of the Tbilisi State University of Ivane Javakhishvili Position Professor, head of the department of applied mathematics 5. -

70 Weli 70 YEARS
soxumis fizika-teqnikis institutis 70 weli Seqmnisa da ganviTarebis etapebi (1945-2015) 70 YEARS OF THE SUKHUMI INSTITUTE OF PHYSICS AND TECHNOLOGY History and Development (1945-2015) ggamomcemlobaamomcemloba ``universali~universali~ TTbilisibilisi 22015015 1 © gg.. bbokuCava,okuCava, 22015015 wwelieli gamomcemloba `universali~, 2015 Tbilisi, 0179, i. WavWavaZis gamz. 19, : 2 22 36 09, 5(99) 17 22 30 E–mail: [email protected] ISBN 978-9941-22-637-3 2 winasityvaoba Foreword mim dina re wels so xu mis ilia ve- ku as fizi ka-teq ni kis in stitu ti (sfti) 70 wlis iubi les aR niSnavs. rTu li da dra ma tu lia (zo gi erT etap ze tragi kulic) insti tu tis da fuZne bi sa da gan vi Ta re bis is- to ria. ma Ra li teq no lo gi e bis uni ka lu- ri centris da ar seba sa qar Tve- loSi pir ve li sab Wo Ta bir Tvu li iara Ris Seqmnas Tan iyo da kav Si- re bu li. insti tu ti ya lib de bo da gamo Ce nili ger ma neli mec ni e re- bis mo na wi le o biT. un da aRi niS- nos, rom esec unika lu ri mov le- naa Cve ni mecni e re bis is to ri a Si - msof li o Si aRi a re bu li ger ma ne- li mec ni e re bis mo na wi le o ba Cve ni This year Ilia Vekua Sukhumi Ins tute mec ni e ru li sko lis Camo ya li be- of Physics and Technology (SIPT) is bis saqme Si. -

Georgia's Nuclear Odyssey
Georgia’s Nuclear Odyssey: The Path from Soviet Atomic Legacy to Global Nonproliferation Regime Tbilisi 2013 Publication supported by Swedish Radiation Safety Authority. Editorial board: Akubardia Teona Lortkipanidze Shorena Pataraia Tamar Mchedlishvili Irakli Scientific Editor: Miles Pomper, the James Martin Centre for Nonproliferation Studies of the Monterey Institute for International Studies Cover Design: Eka Tsagareli Layout Design: Alexander Jikuridze © Civil Council on Defence and Security CCDS The statements and opinions in this publication are those of the individual authors and contributors. ISBN 978-9941-0-6091-5 Contents Introduction ................................................................................................ 5 Nuclear Research in Soviet Georgia ...................................................... 9 Chabashvili M., Japaridze G. I., Lortkipanidze Sh., Pataraia T., Rostomashvili Z. 1. The Early Years ..............................................................................................11 2. Georgian Nuclear Research in the Soviet Era: Pressures and Limits on Scientists ......................................................................................................17 3. The End of the Soviet Era and Beyond ..........................................................34 3.1 Nuclear Research Reactor ..........................................................................34 4. Conclusions ...................................................................................................35 Soviet -
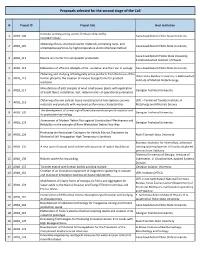
Proposals Selected for the Second Stage of the Call
Proposals selected for the second stage of the Call N Project ID Project title Host institution Complex prolong-acting zeolitic fertilizer obtained by 1 AR18_106 Ivane Javakhishvili Tbilisi State University nanotechnology Obtaining of new structural reactor materials, containing nano- and 2 AR18_107 Ivane Javakhishvili Tbilisi State University ultradisperse particles, by high-temperature electrochemical method Ivane Javakhishvili Tbikisi State University, 3 AR18_111 Plasma arc reactor for nanopowder production E.Andronikashvili Institute of Physics 4 AR18_112 Elaboration of efficient catalysts of CO - oxidation and their use in ecology Ivane Javakhishvili Tbilisi State University Obtaining and studying of biologically active products from the tissue of the Tbilisi State Medical University, V.Bakhutashvili 5 AR18_115 human placenta, the creation of various dosage forms for practical Institute of Medical Biotechnology medicine Manufacture of pilot samples of wind small power plants with application 6 AR18_117 Georgian Technical University of basalt fibers, installation, test, determination of operational parameters Obtaining of boron carbide-based nanostructured heterophase ceramic LEPL – Ferdinand Tavadze Institute of 7 AR18_119 materials and products with improved performance characteristics Metallurgy and Materials Science The development of a new high efficient diamond-composite material and 8 AR18_120 Georgian Technical University its production technology Assessment of Modern Debris Flow against Construction Effectiveness and 9 AR18_123 -

North and South
TEDO DUNDUA NORTH AND SOUTH (Towards the Question of the NATO Enlargement) 1 The author made a grateful use of the grant from NATO Office of Information and Press (NATIP). 2 PREFACE A competition between North and South seems to be a global future challenge with metropol- itan system and agro-industrial confederation as the rivals, the latter moving towards the industrial visage thus ejecting the superpowers from a supply-scheme. A strict physical-geographic definition of North and South is as follows: marine, humid continen- tal, Mediterranean and humid subtropical regions form non-irrigative sector, while semiarid and arid regions – irrigative sector. They will be the opponents. The first one is superindustrial, and the next – a permanent supplier of food and the raw materials from as far back as the Greek times. Such order has supported a normal evolution. But for the Iranian Revolution the situation is abnormal. And what will happen if South accepts this idea? A solution of problem is as follows: a definition of the Abendland should be revised – Abend- land is the West and the East (Slavonic spaces and Georgia, the west part of which is non-irrigative, and the east part _ the extreme north of the irrigative sector). The forces will be distributed as follows: above the equator – industrial North and agro-industrial South; and below the equator _ industrial in prospect South and agro-industrial North. What will the future conflicts be like? There would be none. A short glimpse on a history of the European integration is represented here with Georgia as a participant. -

Modern Mathematics Education for Engineering Curricula in Europe
Seppo Pohjolainen Tuomas Myllykoski Christian Mercat Sergey Sosnovsky Editors Modern Mathematics Education for Engineering Curricula in Europe Modern Mathematics Education for Engineering Curricula in Europe Seppo Pohjolainen • Tuomas Myllykoski • Christian Mercat • Sergey Sosnovsky Editors Modern Mathematics Education for Engineering Curricula in Europe A Comparative Analysis of EU, Russia, Georgia and Armenia Editors Seppo Pohjolainen Tuomas Myllykoski Laboratory of Mathematics Laboratory of Mathematics Tampere University of Technology Tampere University of Technology Tampere, Finland Tampere, Finland Christian Mercat Sergey Sosnovsky Université Lyon 1 Utrecht University IREM de Lyon, Batimentˆ Braconnier Utrecht, The Netherlands Villeurbanne Cedex, France This project has been funded with support from the European Commission. This publication reflects the views only of the author, and the Commission cannot be held responsible for any use which may be made of the information contained therein. ISBN 978-3-319-71415-8 ISBN 978-3-319-71416-5 (eBook) https://doi.org/10.1007/978-3-319-71416-5 Library of Congress Control Number: 2018943911 Mathematics Subject Classification (2010): 97Uxx © The Editor(s) (if applicable) and The Author(s) 2018. This book is an open access publication. Open Access This book is licensed under the terms of the Creative Commons Attribution 4.0 Inter- national License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made. The images or other third party material in this book are included in the book’s Creative Commons license, unless indicated otherwise in a credit line to the material. -

Tsxum-Afxazetis Mecnierebata Akademiis Shromebi 2017 N13-14.Pdf
cxum-afxazeTis mecnierebaTa akademia Tskhum-Abkhazian Academy of Sciences eZRvneba gamoCenili maTematikosisa da meqanikosis, akademikos ilia vekuas dabadebidan 110 wlisTavs Dedicated to the 110th Anniversary of Outstanding Mathematician and Mechanist, Academician Ilia Vekua Tskhum-Abkhazian Academy of Sciences PROCEEDINGS XIII-XIV Publishing House “SAARI” Tbilisi, 2017 cxum-afxazeTis mecnierebaTa akademia S r o m e b i XIII-XIV gamomcemloba `saari~ Tbilisi, 2017 mTavari redaqtori oTar Jordania redaqtorebi: Temur CilaCava, meri gabedava, nona (nazi) uSveriZe pasuxismgebeli mdivani: irma zaqaraia saredaqcio sabWo maria kornelia barliba, rumineTi (kulturologia), badri gogia, safrangeTi (istoria), tania kapiki, saberZneTi (turizmi), anzor miqaia, aSS (qimia), henrik pa- procki, poloneTi (Teologia), liubov soloviova, ruseTi (eTnologia), daviT yolbaia, poloneTi (istoria), maria koniuSkeviCi, belorusi (filologia). saredaqcio kolegia WiaTurisa da saCxeris mitropoliti danieli (daTuaSvili), zoia adamia, diana alania, ekaterine bakaraZe, meri gabedava, nugzar ebanoiZe, eka vardoSvili, anzor ToTaZe, guCa kvaracxelia, medea kvaracxelia, paata koRuaSvili, maia marRania, antonina msxilaZe, nodar naTaZe, qeTevan pavliaSvili, oTar Jordania, avTandil silagaZe, nona (nazi) uSveriZe, gulnara qarCava, malxaz Rvinjilia, manana Selia, vaJa Sengelia, Temur CilaCava, nodar CxartiSvili, givi cincaZe, marat cicqiSvili, mineda Wanturia, nodar WiTanava, gulnaz xuxua, marina jaiani, liliana janaSia, levan jinjixaZe, jemal jinjixaZe. Editor-in-Chief: Otar Zhordania -

Caucasus Journal of Social Sciences
aucasus Journal C of social sciences Volume 11 2018 Politics and International Relations Education History and Anthropology Humanities Law and Art Public Health and Psychology Business and Economics ISSN 1512-3677 www.ug.edu.ge Caucasus Journal of Social Sciences Volume 11 Issue 1 The University of Georgia Publishing House Tbilisi 2018 UDC(uak) 908 (479) (06) k144 Printed at The University of Georgia. Tbilisi, Georgia. Copyright © 2018. All rights reserved by the University of Georgia. Permission to make digital or hard copies of part or all of this work for personal or classroom use is granted without fee provided that copies are not made or distributed for profit or commercial advantage. No responsibility for the views expressed by authors in the Caucasus Journal of Social Sciences is assumed by the editors or the publisher. Caucasus Journal of Social Sciences The University of Georgia. Georgia, Tbilisi, 0175. M. Kostava Street 77, Building IV. Tel: (+995 32) 255 22 22 Email: [email protected] Copyright © 2018 Caucasus Journal of Social Sciences ISSN 1512-3677 Caucasus Journal of Social Sciences Editor-in-Chief Jeremiah Paul Johnson Managing Editor Julieta Andguladze Board of Editors Abuladze Konstantine Tbilisi Teaching University “Gorgasali” Alasania Giuli The University of Georgia Blauvelt Timothy American Councils Carper Mark The University of Alaska Anchorage Davies Janette Oxford University Dzebisashvili Lasha The University of Georgia Ghudushauri Tinatin The University of Georgia Gvelesiani Mariam The University of Georgia -

Recruitment Strategy 2016-17
2016 2016-17 SDSU Georgia Cohort December 4, 2015 RECRUITMENT STRATEGY 2016-17 The 45-month contract between SDSU and MCC/MCA-G calls for submission of a comprehensive strategy paper for recruitment of SDSU-G’s 2016-17 cohort. This strategy paper is prepared as a deliverable of the 45-month contract. The three pillars of the recruitment strategy for the 2016-17 cohort are: 1) Identifying and signing memorandums of understanding (MOU's) with public and private Feeder Schools (mostly private schools); 2) Creation of a STEM Database for Georgia which can then be used for CRM activities to have continuous communication with prospective students, and; 3) Establishing "Pathway" programs with partner universities for international student recruitment. Due to the fact that high schools finished their summer break on September 15, and the fall recruitment season is in full swing, the recruitment strategy described herein is at the same time being implemented. TABLE OF CONTENTS 1. Introduction 2. Situation Analysis 2.1 Country Overview 2.2 Challenges for SDSU 2.3 Last Year’s Recruitment Overview 2.4 SDSU-G 2015-16 Enrollment 3. Methodology 4. Objectives for 2016-17 Recruitment cohort 5. Women in STEM 6. Recruiting Techniques and Tools 7. Activities 7.1 STEM Awareness 7.2 Increase the Interest of fee-paying prospective students 7.3 Making relevant amendments to the Higher Education Legislation 7.4 Increase the Participation of Women 7.5 Socially Vulnerable Student Groups 7.6 NGO and industry participation in STEM education and development 7.7 Retaining Existing Students 7.8 International Student Recruitment 8. -

Jurnali 2020.Cdr
Virtual Commencement 2020 Celebrating our graduates in the COVID era Post-Covid p.6 SDSU Georgia Convocation p.12-13 Nikoloz Khundzakishvili on p.20-22 SDSU Georgia Responds to Ceremony 2019 University/Industry Partnership COVID-19 p. 8 ACS Georgia Chapter p.14-15 Student Clubs at p.26-31 Congratulations to our Established SDSU Georgia Graduating Seniors The Newsletter of San Diego State University Georgia is published by the Student Services department and distributed to SDSU Georgia stakeholders, faculty, students, San Diego State University Georgia, through funding from the Millennium Challenge Corporation (MCC) and and friends. Millennium Challenge Account Georgia (MCA Georgia), offers students an exciting educational opportunity to SAN DIEGO STATE UNIVERSITY study in Tbilisi, Georgia. Here, in the heart of the Caucasus, Adela de la Torre students are able to earn a professionally accredited, internationally recognized U.S. bachelor’s degree. President San Diego State University (SDSU), along with three top Georgian Universities, Georgian Technical University SAN DIEGO STATE UNIVERSITY GEORGIA (GTU), Ilia State University (ISU), and Tbilisi State Halil Güven University (TSU), offers internationally accredited Dean bachelor’s degrees in science, technology, engineering and mathematics (STEM) fields. Programs offered by the university support the development of engineering, Newsletter created by science, and technology fields, as well as Georgia’s human Editor-in-chief and writer capital capacity for economic growth. Cherish Broker In five