The Muon Puzzle in Cosmic-Ray Induced Air Showers and Its Connection to the Large Hadron Collider
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Very Forward Photon Production in Proton-Proton Collisions Measured by the Lhcf Experiment at the Large Hadron Collider
Very forward photon production in proton-proton collisions measured by the LHCf experiment at the Large Hadron Collider Author: Alessio Tiberio Supervisor: Lorenzo Bonechi The LHC-forward (LHCf) experiment, situated at the LHC accelerator, has measured neutral particles production in a very forward region (pseudo-rapidity η > 8:4) in proton-proton and proton- lead collisions. The main purpose of the LHCf experiment is to test hadronic interaction models used in ground based cosmic rays experiments to simulate cosmic rays induced air-showers in the Earth's atmosphere. Highest energy cosmic rays can only be detected from secondary particles which are produced by the interaction of the primary particle with nuclei of the atmosphere. Studying the development of air showers, it is possible to reconstruct the type and kinematic parameters of primary particle. For this reason, Monte Carlo (MC) simulations with accurate hadronic interaction models are needed to reproduce the development of air-showers. Since the energy flow of secondary particles is concentrated in the forward direction, measurements of particle production at high pseudo-rapidity (i.e. small angles) are very important. Furthermore, soft QCD interactions (non perturbative regime) dominates in the very forward region and MC simulations of air showers are based on phenomenological model, so inputs from experimental data are crucial. The experiment is composed by two independent detectors (Arm1 and Arm2 ) located at 140 m from the ATLAS's interaction point (IP1) on opposite sides [1]. Detectors are placed inside the Target Neutral Absorber (TAN), where the beam pipe from IP1 turns into two separates tubes: the position between the two beam pipes allows to measure particles produced at zero degrees. -

Detection of Cosmic Rays at the LHC Detection of Cosmic Rays at the LHC
Particle and Astroparticle Physics at the Large Hadron Collider --Hadronic Interactions-- Albert De Roeck CERN, Geneva, Switzerland Antwerp University Belgium UC-Davis California USA NTU, Singapore November 15th 2019 Outline • Introduction on the LHC and LHC physics program • LHC results for Astroparticle physics • Measurements of event characteristics at 13 TeV • Forward measurements • Cosmic ray measurements • LHC and light ions? • Summary The LHC Machine and Experiments MoEDAL LHCf FASER totem CM energy → Run-1: (2010-2012) 7/8 TeV Run-2: (2015-2018) 13 TeV -> Now 8 experiments Run-2 starts proton-proton Run-2 finished 24/10/18 6:00am 2018 2010-2012: Run-1 at 7/8 TeV CM energy Collected ~ 27 fb-1 2015-2018: Run-2 at 13 TeV CM Energy Collected ~ 140 fb-1 2021-2023/24 : Run-3 Expect ⇨ 14 TeV CM Energy and ~ 200/300 fb-1 The LHC is also a Heavy Ion Collider ALICE Data taking during the HI run • All experiments take AA or pA data (except TOTEM) Expected for Run-3: in addition short pO and OO runs ⇨ pO certainly of interest for Cosmic Ray Physics Community! 4 10 years of LHC Operation • LHC: 7 TeV in March 2010 ->The highest energy in the lab! • LHC @ 13 TeV from 2015 onwards March 30 2010 …waiting.. • Most important highlight so far: …since 4:00 am The discovery of a Higgs boson • Many results on Standard Model process measurements, QCD and particle production, top-physics, b-physics, heavy ion physics, searches, Higgs physics • Waiting for the next discovery… -> Searches beyond the Standard Model 12:58 7 TeV collisions!!! New Physics Hunters -
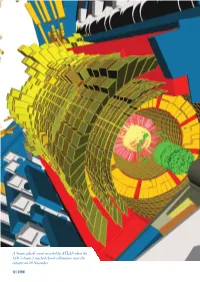
Event Recorded by ATLAS When the LHC's Beam 2 Reached Closed
A ‘beam splash’ event recorded by ATLAS when the LHC’s beam 2 reached closed collimators near the detector on 20 November. 12 | CERN “The imminent start-up of the LHC is an event that excites everyone who has an interest in the fundamental physics of the Universe.” Kaname Ikeda, ITER Director-General, CERN Bulletin, 19 October 2009. Physics and Experiments The moment that particle physicists around the world had been The EMCal is an upgrade for ALICE, having received full waiting for finally arrived on 20 November 2009 when protons approval and construction funds only in early 2008. It will detect circulated again round the LHC. Over the following days, the high-energy photons and neutral pions, as well as the neutral machine passed a number of milestones, from the first collisions component of ‘jets’ of particles as they emerge from quark� at 450 GeV per beam to collisions at a total energy of 2.36 TeV gluon plasma formed in collisions between heavy ions; most — a world record. At the same time, the LHC experiments importantly, it will provide the means to select these events on began to collect data, allowing the collaborations to calibrate line. The EMCal is basically a matrix of scintillator and lead, detectors and assess their performance prior to the real attack which is contained in ‘supermodules’ that weigh about eight tonnes. It will consist of ten full supermodules and two partial on high-energy physics in 2010. supermodules. The repairs to the LHC and subsequent consolidation work For the ATLAS Collaboration, crucial repair work included following the incident in September 2008 took approximately modifications to the cooling system for the inner detector. -

Sub Atomic Particles and Phy 009 Sub Atomic Particles and Developments in Cern Developments in Cern
1) Mahantesh L Chikkadesai 2) Ramakrishna R Pujari [email protected] [email protected] Mobile no: +919480780580 Mobile no: +917411812551 Phy 009 Sub atomic particles and Phy 009 Sub atomic particles and developments in cern developments in cern Electrical and Electronics Electrical and Electronics KLS’s Vishwanathrao deshpande rural KLS’s Vishwanathrao deshpande rural institute of technology institute of technology Haliyal, Uttar Kannada Haliyal, Uttar Kannada SUB ATOMIC PARTICLES AND DEVELOPMENTS IN CERN Abstract-This paper reviews past and present cosmic rays. Anderson discovered their existence; developments of sub atomic particles in CERN. It High-energy subato mic particles in the form gives the information of sub atomic particles and of cosmic rays continually rain down on the Earth’s deals with basic concepts of particle physics, atmosphere from outer space. classification and characteristics of them. Sub atomic More-unusual subatomic particles —such as particles also called elementary particle, any of various self-contained units of matter or energy that the positron, the antimatter counterpart of the are the fundamental constituents of all matter. All of electron—have been detected and characterized the known matter in the universe today is made up of in cosmic-ray interactions in the Earth’s elementary particles (quarks and leptons), held atmosphere. together by fundamental forces which are Quarks and electrons are some of the elementary represente d by the exchange of particles known as particles we study at CERN and in other gauge bosons. Standard model is the theory that laboratories. But physicists have found more of describes the role of these fundamental particles and these elementary particles in various experiments. -

Particle Accelerators and Experiments Albert De Roeck CERN, Geneva, Switzerland Antwerp University Belgium UC-Davis California USA NTU, Singapore
Particle Accelerators and Experiments Albert De Roeck CERN, Geneva, Switzerland Antwerp University Belgium UC-Davis California USA NTU, Singapore March 30th- April 2nd Muscat 1 Part I Accelerators 2 Different types of Methodology tools and equipment are needed to observe different sizes of object Only particle accelerators can explore the tiniest objects in the 5 Universe 5 Accelerators are Powerful Microscopes Planck constant They make high energy particle beams h = momentum that allow us to see small things. wavelength p ~ energy seen by low energy seen by high energy beam of particles beam of particles (poorer resolution) (better resolution) High Energy Physics Experiments Rutherford experiment (1909) Centre of mass energy squared s=E1m2 Centre of mass energy squared s=4E1E2 Detectors techniques have followed these developments Accelerators for Charged Particles 9 Recent High Energy Colliders Highest energies can be reached with proton colliders Machine Year Beams Energy (s) Luminosity SPPS (CERN) 1981 pp 630-900 GeV 6.1030cm-2s-1 Tevatron (FNAL) 1987 pp 1800-2000 GeV 1031-1032cm-2s-1 SLC (SLAC) 1989 e+e- 90 GeV 1030cm-2s-1 LEP (CERN) 1989 e+e- 90-200 GeV 1031-1032cm-2s-1 HERA (DESY) 1992 ep 300 GeV 1031-1032cm-2s-1 RHIC (BNL) 2000 pp /AA 200-500 GeV 1032cm-2s-1 LHC (CERN) 2009 pp (AA) 7-14 TeV 1033-1034cm-2s-1 Luminosity = number of events/cross section/sec • Limits on circular machines – Proton colliders: Dipole magnet strength superconducting magnets – Electron colliders: Synchrotron10 radiation/RF power: loss ~E4/R2 How Many Accelerators Worldwide? a) 1-10 b) 10-100 c) 100-1,000 d) 1,000-10,000 e) > 10,000 11 Accelerators Worldwide > 25,000 accelerators in use 12 Accelerators Worldwide 44% Radio- therapy 13 Accelerators Worldwide 44% 40% Radio- Ion therapy implant. -

Femtoscopy of Proton-Proton Collisions in the ALICE Experiment
Femtoscopy of proton-proton collisions in the ALICE experiment DISSERTATION Presented in Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy in the Graduate School of The Ohio State University By Nicolas Bock, B.Sc. B.Eng., M.Sc. Graduate Program in Physics The Ohio State University 2011 Dissertation Committee: Professor Thomas J. Humanic, Advisor Professor Michael Lisa #1 Professor Klaus Honscheid #2 Professor Richard Furnstahl #3 c Copyright by Nicolas Bock 2011 Abstract The Large Ion Collider Experiment (ALICE) at CERN has been designed to study matter at extreme conditions of temperature and pressure, with the long term goal of observing deconfined matter (free quarks and gluons), study its properties and learn more details about the phase diagram of nuclear matter. The ALICE experiment provides excellent particle tracking capabilities in high multiplicity proton-proton and heavy ion collisions, allowing to carry out detailed research of nuclear matter. This dissertation presents the study of the space time structure of the particle emission region, also known as femtoscopy, in proton- proton collisions at 0.9, 2.76 and 7.0 TeV. The emission region can be characterized by taking advantage of the Bose-Einstein effect for identical particles, which causes an enhancement of produced identical pairs at low relative momentum. The geometry of the emission region is related to the relative momentum distribution of all pairs by the Fourier transform of the source function, therefore the measurement of the final relative momentum distribution allows to extract the initial space-time characteristics. Results show that there is a clear dependence of the femtoscopic radii on event multiplicity as well as transverse momentum, a signature of the transition of nuclear matter into its fundamental components and also of strong interaction among these. -

Results from Lhcf Experiment
EPJ Web of Conferences 28, 02003 (2012) DOI: 10.1051/epjconf/ 20122802003 C Owned by the authors, published by EDP Sciences, 2012 Results from LHCf Experiment Alessia Tricomi on behalf of the LHCf Collaboration University of Catania and INFN Catania, Italy √ Abstract.√ The LHCf experiment has taken data in 2009 and 2010 p-p collisions at LHC at s = 0.9 TeV and s = 7 TeV. The measurement of the forward neutral particle spectra produced in proton-proton collisions at LHC up to an energy of 14 TeV in the center of mass system are of fundamental importance to calibrate the Monte Carlo models widely used in the high energy cosmic ray (HECR) field, up to an equivalent laboratory energy of the order of 1017 eV. In this paper the first results on the inclusive photon spectrum measured by LHCf is reported. Comparison of this spectrum with the model expectations show significant discrepancies, mainly in the high energy region. In addition, perspectives for future analyses as well as the program for the next data taking period, in particular the possibility to take data in p-Pb collisions, will be discussed. 1 Introduction Each calorimeter (ARM1 and ARM2) has a double tower structure, with the smaller tower located at zero degree col- The LHCf experiment at LHC has been designed to cali- lision angle, approximately covering the region with pseudo- brate the hadron interaction models used in High Energy rapidity η > 10 and the larger one, approximately cover- Cosmic Ray (HECR) Physics through the measurement of ing the region with 8.4 < η < 10. -

Lambda and Anti-Labmda Production in the ALICE Experiment at the LHC
LLNL-TR-643836 Lambda and Anti-Labmda production in the ALICE experiment at the LHC. R. Carmona, R. Soltz September 12, 2013 Disclaimer This document was prepared as an account of work sponsored by an agency of the United States government. Neither the United States government nor Lawrence Livermore National Security, LLC, nor any of their employees makes any warranty, expressed or implied, or assumes any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process, or service by trade name, trademark, manufacturer, or otherwise does not necessarily constitute or imply its endorsement, recommendation, or favoring by the United States government or Lawrence Livermore National Security, LLC. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States government or Lawrence Livermore National Security, LLC, and shall not be used for advertising or product endorsement purposes. This work performed under the auspices of the U.S. Department of Energy by Lawrence Livermore National Laboratory under Contract DE-AC52-07NA27344. Strangeness Production in Jets with ALICE at the LHC Rodney Carmona, Mike Tyler II, Ron Soltz, Austin Harton, Edmundo Garcia Chicago State University, Lawrence Livermore National Laboratory Cern (European Organization for Nuclear Research) At this laboratory Physicists and Engineers study fundamental particles using the world’s largest and most complex instruments. Here particles are made to collide at close to the speed of light to see how they interact and help to discover the basic laws of nature. -

Energy Spectrum of Neutral Pion at LHC Proton-Proton Collisions Measured by the Lhcf Ex- Periment
32ND INTERNATIONAL COSMIC RAY CONFERENCE,BEIJING 2011 Energy spectrum of neutral pion at LHC proton-proton collisions measured by the LHCf ex- periment. H. MENJO1,O.ADRIANI2,3,L.BONECHI2,M.BONGI2,G.CASTELLINI2,3, R. D’ALESSANDRO2,3 K. FUKATSU4, M. HAGUENAUER5,Y.ITOW1,4,K.KASAHARA6, K.KAWADE4,D.MACINA7,T.MASE4,K.MASUDA4,G. MITSUKA4,Y.MURAKI4,M.NAKAI6,K.NODA8,P.PAPINI2, A.-L. PERROT7,S.RICCIARINI2,9,T.SAKO1,4, Y. S HIMIZU6,K.SUZUKI4,T.SUZUKI6,K.TAKI4,T.TAMURA10,S.TORII6,A.TRICOMI8,11,W.C.TURNER12 1Kobayashi-Maskawa Institute for the Origin of Particles and the Universe, Nagoya University, Nagoya, Japan 2INFN Section of Florence, Italy 3University of Florence, Italy 4Solar-Terrestrial Environment Laboratory, Nagoya University, Nagoya, Japan 5Ecole-Polytechnique, Palaiseau, France 6RISE, Waseda University, Japan 7CERN, Switzerland 8INFN Section of Catania, Italy 9Centro Siciliano di Fisica Nucleare e Struttura della Materia, Catania, Italy 10Kanagawa University, Japan 11University of Catania, Italy 12LBNL, Berkeley, California, USA '[email protected] ,,&5&9 Abstract: The LHCf experiment is an LHC forward experiment dedicated to high energy cosmic-ray physics. The LHCf has completed the first phase of physics program, data taking at √s=900 GeV and 7 TeV proton-proton collisions, in July 2010. The LHCf detectors have capability of measurement of forward π0 with more than 600 GeV by reconstruction from photon pairs measured by the two calorimeter towers. A data set taken by the Arm2 detector in 15 May 2010 was analyzed. In this paper, the measured π0 energy spectrum is presented. -

Upgrade of the Global Muon Trigger for the Compact Muon Solenoid Experiment at CERN
DISSERTATION/DOCTORAL THESIS Titel der Dissertation/Title of the Doctoral Thesis “Upgrade of the Global Muon Trigger for the Compact Muon Solenoid experiment at CERN” verfasst von/submitted by Mag. Dinyar Sebastian Rabady angestrebter akademischer Grad/in partial fulfilment of the requirements for the degree of Doktor der Naturwissenschaften (Dr. rer. nat.) CERN-THESIS-2018-033 25/04/2018 Wien, im Jänner 2018/Vienna, in January 2018 Studienkennzahl lt. Studienblatt/ A 796 605 411 degree programme code as it appears on the student record sheet: Studienrichtung lt. Studienblatt/ Physik field of study as it appears onthe student record sheet: Betreut von/Supervisor: Dipl.-Ing. Dr. Claudia-Elisabeth Wulz Hon.-Prof. Dipl.-Phys. Dr. Eberhard Widmann Für meinen Großvater. Abstract The Large Hadron Collider is a large particle accelerator at the CERN research labo- ratory, designed to provide particle physics experiments with collisions at unprece- dented centre-of-mass energies. For its second running period both the number of colliding particles and their collision energy were increased. To cope with these more challenging conditions and maintain the excellent performance seen during the first running period, the Level-1 trigger of the Compact Muon Solenoid experiment — a so- phisticated electronics system designed to filter events in real-time — was upgraded. This upgrade consisted of the complete replacement of the trigger electronics andafull redesign of the system’s architecture. While the calorimeter trigger path now follows a time-multiplexed processing model where the entire trigger data for a collision are received by a single processing board, the muon trigger path was split into regional track finding systems where each newly introduced track finder receives data from all three muon subdetectors for a certain geometric detector slice and reconstructs fully formed muon tracks from this. -

Lhcf Sits in a Straight Line from the Collision Point, and So Can Detect ‘Forward Moving’ Particles
Forward During a collision many different particles are flung out in all directions, but the highest energy particles are scattered forwards - in almost the same direction as the beams inside the LHC. Straight ahead Unlike the four big LHC experiments, LHCf sits in a straight line from the collision point, and so can detect ‘forward moving’ particles. These are very similar to the particles created when an ultra-high-energy cosmic ray hits the Earth’s atmosphere. The results will help in the search for the origins of these mysterious cosmic rays. Double detectors LHCf is made up of two independ- ATLAS collision point The Large Hadron Collider forward Experiment ent detectors located in the LHC tunnel, 140 metres either side of LHCf detector 2 the huge ATLAS experimental cav- ern. LHCf The Earth’s upper atmosphere is constantly hit by a storm of Each detector is placed along the particles called cosmic rays. These particles collide with the nuclei beam pipe, at the point where the in the upper atmosphere producing many secondary particles, pipe splits into two. Here they will which in turn collide with other nuclei in the atmosphere. look at neutral particles, which are unaffected by the very strong magnetic fields that guide the This cascade continues, producing a shower of particles that positively charged proton beams Neutral secondary reach the ground. The size of this particle shower depends on around the LHC. particles the energy of the cosmic ray. Before reaching the LHCf detectors, A huge number of cosmic rays hit the Earth’s atmosphere every the LHC protons are directed into LHCf detector 1 second, but occasionally one arrives with so much energy two separate beam pipes, while the neutral particles carry straight on that it produces an enormous shower of billions of secondary into the detectors. -

Vocational Acqusition of Stem Teachers in Cern Workshops
Education Research Highlights in Mathematics, Science and Technology 2016 VOCATIONAL ACQUSITION OF STEM TEACHERS IN CERN WORKSHOPS Mustafa Hilmi ÇOLAKOĞLU Ministry of National Education, Turkey ABSTRACT: Louis De Broglie suggested the building of atomic physics laboratory in European Culture Conference that was held on 9th December 1949 in order to provide the previous achievement and dynamism to Europe in the fundamental sciences after the World War II. Isidor Rabi also suggested the building of a regional laboratory in 5th UNESCO Conference which was held in Florence, 1950 in order to develop the international scientific cooperation. Eleven countries decided to establish a European Council for Nuclear Research in Paris, 1951. Establishing treaty was signed by 12 countries in 1953. Approvals from the parliaments of Denmark, France, West Germany, Greece, Italy, Netherlands, Norway, Sweden, Switzerland, UK and Yugoslavia were completed on 29th September 1954, and CERN European Organization for Nuclear Research” was established (CERN, 2016). Today, CERN, having 21 members and 4.000 researchers, is the largest accelerator and research laboratory of the world, and is the center of excellence that provides opportunity to develop numerous technological products as well as many scientific discoveries. Innovations, which facilitate our lives from health to communication, energy to material science, security to food sector in every field, emerge through technological devices and systems such as particle accelerators and detectors that are developed by and used in CERN. There are full-scale experiments which are maintained, renovated or at the construction phase today as always being, or designed for future in CERN that is the biggest international scientific and technologic corporation organization of the world (Ankara University, 2016a).