DOCSLIB.ORG

CS106X Handout

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
CS106X Handout CS107 Cynthia Lee Winter 2017 CS107 Final Exam (Practice #1) You have 3 hours to complete all problems. You don’t need to #include any libraries, and you needn’t use assert to guard against any errors. Understand that the majority of points are awarded for concepts taught in CS107, and not prior classes. You don’t get many points for for-loop syntax, but you certainly get points for proper use of &, *, and the low-level C functions introduced in the course. Problem Points Score Grader 1. Number 5 representation 2. Generics, pointers, and 10 CVector 3. Assembly and 17 optimizations 4. Build process 10 5. Heap allocator 18 6. Cache design 6 TOTAL 66 Problem 1: Number Representation (5pts) (a) (2pts) Write the minifloat representation of the decimal value -5/8. Recall that minifloat is a (made-up) 8-bit floating point format with 1 sign bit, 4 exponent bits, and 3 mantissa bits. Write your answer as a bit pattern in these boxes: fraction = Scratch work space: (b) (1pt) What is the binary equivalent of the following hexadecimal number? 0xCAFE0 (Write your answer in the box.) (c) (2pt) What does the following code print? (Write your answer in the box.) unsigned int moana = 0xFFFFFFCC; int maui = (int)moana; printf("%d", maui); Problem 2: Generics, pointers, and CVector (10 points) (a) (4pts) You would like to use a CVector to hold your CS107 assignment grade information. Each entry in the CVector will be a struct that holds information for one assignment. The struct is defined below, and we also show an excerpt of code that calls cvec_create: typedef struct { int num; // assignment number, e.g., 4 for assign4 double score; // your score as pct, e,g., 0.92 for 46/50 char *letter_grade;// your letter grade as a string, e.g., "A-" } assignT; // excerpt of code where cvec_create is called CVector *grades = cvec_create(sizeof(assignT), 8, assign_cleanup); // end excerpt Write a callback function that can be passed to cvec_create that will appropriately clean up memory for your grades vector so there will be no leaks. Assume that any memory associated that could possibly need freeing in this callback should be freed in this callback. In particular, assume the letter grade strings were created using strdup. void assign_cleanup(void *assign) { } [For parts (b), (c)] Recall our generic “swap” function from class (reproduced below). It is used to make two values trade places in memory, and is commonly used in sorting arrays. There’s a right way to call this swap function in normal circumstances, but we’re asking you to use it a bit “creatively” to achieve particular results. Note: what matters for the correctness of these results is that the output if you ran this “for (int i = 0; i < 5; i++) printf("%d %d ", ptr1[i], ptr2[i]);” after the call to swap_any matches what it would be for the “after” diagram shown. void swap_any(void *a, void *b, size_t sz) { char tmp[sz]; memcpy(tmp, a, sz); memcpy(a, b, sz); memcpy(b, tmp, sz); } (b) (3pts) Complete the mixup1 function to create this before & after result. Your solution must consist of ONLY completing the arguments of the one call to swap_any, as shown. Before: After: ptr1 ptr2 ptr1 ptr2 void mixup1() { int *ptr1 = malloc(5 * sizeof(int)); int *ptr2 = malloc(5 * sizeof(int)); 1 6 8 6 for (int i = 1; i <= 5; i++) { ptr1[i-1] = i; 2 7 9 7 ptr2[i-1] = i + 5; 8 10 3 1 } 4 9 4 2 swap_any(____________________________, 5 10 5 3 ____________________________, ___________________________); } (c) (3pts) Complete the mixup2 function to create this before & after result. Your solution must consist of ONLY completing the arguments of the one call to swap_any, as shown. In this case (part (c)), the third argument should not be edited other than to specify a single argument (that should be a standard type) to sizeof(). Before: After: ptr1 ptr2 ptr1 ptr2 void mixup2() { int *ptr1 = malloc(5 * sizeof(int)); int *ptr2 = malloc(5 * sizeof(int)); for (int i = 1; i <= 5; i++) { 1 6 6 1 ptr1[i-1] = i; 2 7 7 2 ptr2[i-1] = i + 5; 3 8 8 3 } 4 9 9 4 swap_any(____________________________, 5 10 10 5 ____________________________, sizeof(_________)); } Problem 3: Assembly and optimizations (17 points) Consider the following x86-64 code output by gcc using the settings we use for this class (-Og): <ham>: mov (%rdi),%eax lea (%rax,%rax,2),%esi add %esi,%esi mov $0x0,%ecx imul $0x31,%esi jmp L1 L3: lea (%rcx,%rax,1),%edx movslq %edx,%rdx mov %esi,(%rdi,%rdx,4) add $0x2,%eax jmp L2 L4: mov %ecx,%eax L2: cmp $0x9,%eax jle L3 add $0x3,%ecx L1: cmp $0x9,%ecx jle L4 mov $0xa,%eax retq Refer back to this code to answer the questions in parts (a)-(d), on the following pages. (a) (8pts) Fill in the C code below so that it is consistent with the above x86-64 code. Your C code should fit the blanks as shown, so do not try to squeeze in additional lines or otherwise circumvent this (this may mean slightly adjusting the syntax or style of your initial decoding guess to an equivalent version that fits). Your C code should not include any casting. Note that with the compiler set to –Og, some optimization has been performed. One thing you’ll notice right away is that gcc chose not to create an actual eliza array, but instead kept track of its values in other ways. We will ask about optimizations in more detail in later parts of this question. int ham(int *burr) { int eliza[4]; eliza[0] = 7; eliza[1] = 7; eliza[2] = 1; eliza[3] = _____________ * burr[0]; // part (b) for (int i = 0; i < ___________; i+=___________) { for (int j = ___________; j < ___________; j+=___________) { burr[__________] = eliza[0] * eliza[1] * eliza[2] * eliza[3]; //(c) } } if (eliza[0] > eliza[1]) { // part (d) return 8; } if (burr[0] < burr[1] && burr[0] > burr[1]) { // part (d) return 9; } return ___________; } Here is a list of optimizations that we discussed in class. Use it to answer parts (b), (c). i. Constant folding ii. Common subexpression elimination iii. Dead code iv. Strength reduction v. Code motion vi. Tail recursion vii. Loop unrolling (b) (2pts) Refer back to the C code, on the line marked for part (b). It reads: eliza[3] = … * burr[0]; Which optimization from the list most closely relates to this implementation? ______ Name and explain the instruction(s) that implement this product, and explain why gcc would choose to do it that way. (c) (3pts) Refer back to the C code, on the line marked for part (c). It reads: burr[…] = eliza[0] * eliza[1] * eliza[2] * eliza[3]; Which two optimizations from the list most closely relate to when and how this product is calculated? ______ ______ Name and explain the instruction(s) that calculate this product off all the eliza terms: (d) (2pts) Refer back to the C code, on the two lines marked for part (d). (Two if statements.) Neither if statement appears in the assembly code at all, because they are “dead code.” However, the reasons they are considered dead code are slightly different in each case. Explain each case below: How does gcc know that the first if statement is dead code? How does gcc know that the second if statement is dead code? (e) (1pt) In class, we looked at the following simple array sum function, where the order of summing the elements of the array is dictated by the provided indexes array (it contains some permutation of the numbers [0, ..., n-1]): static int sum_fwd_ind(int a[], int n, int indexes[]) { int sum = 0; for (int i = 0; i < n; i++) sum += a[indexes[i]]; return sum; } We saw in class that, for large arrays, this function performs about 3 times faster when indexes is sorted in ascending order than when indexes is in random order. Explain why this can happen even though the code is the same. Problem 4: Build process (10 points) For this problem, you are presented with five small programs, along with the commands that in theory can be used to build and execute them. You should write something about each of the six programs, as follows: Assume we compile using: gcc –Wall –o prog prog.c, and attempt to run the prog executable (if one was generated) with three arguments, like this: “arg1 arg2 arg3”. If any warnings or errors are issued during the build process, you should identify which component(s) issue the warning(s) and/or error(s) by circling all applicable responses. If everything builds (with or without warning(s)) say what will happen when it is executed by circling a response. Remember that if any step gives an error, subsequent steps do not occur (so do not circle them for warnings/errors), and an executable is not produced (so circle “N/A” for the executable part). There is no need to provide an explanation, just circle. The programs aren’t intended to do anything meaningful, as they’re contrived to exercise your understanding of the build process and the C runtime. Note that when #include directives you might expect are NOT used in a program, that’s quite intentional! (a) (2pts) Consider the following program: int strcmp(const char *s1, const char *s2); int main(int argc, const char *argv[]) { return strcmp(argv[0], argv[1]); } Which component(s) complain with warning(s) and/or error(s)? (circle ALL that apply) Preprocessor Compiler Linker N/A (no warnings or errors) If an executable is produced, what happens when you run it? (circle ONE) NO crash MAY crash SURE crash N/A (earlier error) (b) (2pts) Consider the following program: #define PURPLE_RAIN return int main(int argc, const char *argv[]) { if (strlen(argv[0]) > strlen(argv[3])) PURPLE_RAIN argc; else PURPLE_RAIN argc + 1; } Which component(s) complain with warning(s) and/or error(s)? (circle ALL that apply) Preprocessor
Load more

Recommended publications
  • Lab 7: Floating-Point Addition 0.0
    Lab 7: Floating-Point Addition 0.0 Introduction In this lab, you will write a MIPS assembly language function that performs floating-point addition. You will then run your program using PCSpim (just as you did in Lab 6). For testing, you are provided a program that calls your function to compute the value of the mathematical constant e. For those with no assembly language experience, this will be a long lab, so plan your time accordingly. Background You should be familiar with the IEEE 754 Floating-Point Standard, which is described in Section 3.6 of your book. (Hopefully you have read that section carefully!) Here we will be dealing only with single precision floating- point values, which are formatted as follows (this is also described in the “Floating-Point Representation” subsec- tion of Section 3.6 in your book): Sign Exponent (8 bits) Significand (23 bits) 31 30 29 ... 24 23 22 21 ... 0 Remember that the exponent is biased by 127, which means that an exponent of zero is represented by 127 (01111111). The exponent is not encoded using 2s-complement. The significand is always positive, and the sign bit is kept separately. Note that the actual significand is 24 bits long; the first bit is always a 1 and thus does not need to be stored explicitly. This will be important to remember when you write your function! There are several details of IEEE 754 that you will not have to worry about in this lab. For example, the expo- nents 00000000 and 11111111 are reserved for special purposes that are described in your book (representing zero, denormalized numbers and NaNs).
    [Show full text]
  • The Hexadecimal Number System and Memory Addressing
    C5537_App C_1107_03/16/2005 APPENDIX C The Hexadecimal Number System and Memory Addressing nderstanding the number system and the coding system that computers use to U store data and communicate with each other is fundamental to understanding how computers work. Early attempts to invent an electronic computing device met with disappointing results as long as inventors tried to use the decimal number sys- tem, with the digits 0–9. Then John Atanasoff proposed using a coding system that expressed everything in terms of different sequences of only two numerals: one repre- sented by the presence of a charge and one represented by the absence of a charge. The numbering system that can be supported by the expression of only two numerals is called base 2, or binary; it was invented by Ada Lovelace many years before, using the numerals 0 and 1. Under Atanasoff’s design, all numbers and other characters would be converted to this binary number system, and all storage, comparisons, and arithmetic would be done using it. Even today, this is one of the basic principles of computers. Every character or number entered into a computer is first converted into a series of 0s and 1s. Many coding schemes and techniques have been invented to manipulate these 0s and 1s, called bits for binary digits. The most widespread binary coding scheme for microcomputers, which is recog- nized as the microcomputer standard, is called ASCII (American Standard Code for Information Interchange). (Appendix B lists the binary code for the basic 127- character set.) In ASCII, each character is assigned an 8-bit code called a byte.
    [Show full text]
  • Midterm-2020-Solution.Pdf
    HONOR CODE Questions Sheet. A Lets C. [6 Points] 1. What type of address (heap,stack,static,code) does each value evaluate to Book1, Book1->name, Book1->author, &Book2? [4] 2. Will all of the print statements execute as expected? If NO, write print statement which will not execute as expected?[2] B. Mystery [8 Points] 3. When the above code executes, which line is modified? How many times? [2] 4. What is the value of register a6 at the end ? [2] 5. What is the value of register a4 at the end ? [2] 6. In one sentence what is this program calculating ? [2] C. C-to-RISC V Tree Search; Fill in the blanks below [12 points] D. RISCV - The MOD operation [8 points] 19. The data segment starts at address 0x10000000. What are the memory locations modified by this program and what are their values ? E Floating Point [8 points.] 20. What is the smallest nonzero positive value that can be represented? Write your answer as a numerical expression in the answer packet? [2] 21. Consider some positive normalized floating point number where p is represented as: What is the distance (i.e. the difference) between p and the next-largest number after p that can be represented? [2] 22. Now instead let p be a positive denormalized number described asp = 2y x 0.significand. What is the distance between p and the next largest number after p that can be represented? [2] 23. Sort the following minifloat numbers. [2] F. Numbers. [5] 24. What is the smallest number that this system can represent 6 digits (assume unsigned) ? [1] 25.
    [Show full text]
  • 2018-19 MAP 160 Byte File Layout Specifications
    2018-19 MAP 160 Byte File Layout Specifications OVERVIEW: A) ISAC will provide an Eligibility Status File (ESF) record for each student to all schools listed as a college choice on the student’s Student Aid Report (SAR). The ESF records will be available daily as Record Type = 7. ESF records may be retrieved via the File Extraction option in MAP. B) Schools will transmit Payment Requests to ISAC via File Transfer Protocol (FTP) using the MAP 160byte layout and identify these with Record Type = 4. C) When payment requests are processed, ISAC will provide payment results to schools through the MAP system. The payment results records can be retrieved in the 160 byte format using the MAP Payment Results File Extraction Option. MAP results records have a Record Type = 5. The MAP Payment Results file contains some eligibility status data elements. Also, the same student record may appear on both the Payment Results and the Eligibility Status extract files. Schools may also use the Reports option in MAP to obtain payment results. D) To cancel Payment Requests, the school with the current Payment Results record on ISAC's Payment Database must transmit a matching record with MAP Payment Request Code = C, with the Requested Award Amount field equal to zero and the Enrollment Hours field equal to 0 along with other required data elements. These records must be transmitted to ISAC as Record Type = 4. E) Summary of Data Element Changes, revision (highlighted in grey) made to the 2018-19 layout. NONE 1 2018-19 MAP 160 Byte File Layout Specifications – 9/17 2018-19 MAP 160 Byte File Layout Specifications F) The following 160 byte record layout will be used for transmitting data between schools and ISAC.
    [Show full text]
  • POINTER (IN C/C++) What Is a Pointer?
    POINTER (IN C/C++) What is a pointer? Variable in a program is something with a name, the value of which can vary. The way the compiler and linker handles this is that it assigns a specific block of memory within the computer to hold the value of that variable. • The left side is the value in memory. • The right side is the address of that memory Dereferencing: • int bar = *foo_ptr; • *foo_ptr = 42; // set foo to 42 which is also effect bar = 42 • To dereference ted, go to memory address of 1776, the value contain in that is 25 which is what we need. Differences between & and * & is the reference operator and can be read as "address of“ * is the dereference operator and can be read as "value pointed by" A variable referenced with & can be dereferenced with *. • Andy = 25; • Ted = &andy; All expressions below are true: • andy == 25 // true • &andy == 1776 // true • ted == 1776 // true • *ted == 25 // true How to declare pointer? • Type + “*” + name of variable. • Example: int * number; • char * c; • • number or c is a variable is called a pointer variable How to use pointer? • int foo; • int *foo_ptr = &foo; • foo_ptr is declared as a pointer to int. We have initialized it to point to foo. • foo occupies some memory. Its location in memory is called its address. &foo is the address of foo Assignment and pointer: • int *foo_pr = 5; // wrong • int foo = 5; • int *foo_pr = &foo; // correct way Change the pointer to the next memory block: • int foo = 5; • int *foo_pr = &foo; • foo_pr ++; Pointer arithmetics • char *mychar; // sizeof 1 byte • short *myshort; // sizeof 2 bytes • long *mylong; // sizeof 4 byts • mychar++; // increase by 1 byte • myshort++; // increase by 2 bytes • mylong++; // increase by 4 bytes Increase pointer is different from increase the dereference • *P++; // unary operation: go to the address of the pointer then increase its address and return a value • (*P)++; // get the value from the address of p then increase the value by 1 Arrays: • int array[] = {45,46,47}; • we can call the first element in the array by saying: *array or array[0].
    [Show full text]
  • Bits and Bytes
    BITS AND BYTES To understand how a computer works, you need to understand the BINARY SYSTEM. The binary system is a numbering system that uses only two digits—0 and 1. Although this may seem strange to humans, it fits the computer perfectly! A computer chip is made up of circuits. For each circuit, there are two possibilities: An electric current flows through the circuit (ON), or An electric current does not flow through the circuit (OFF) The number 1 represents an “on” circuit. The number 0 represents an “off” circuit. The two digits, 0 and 1, are called bits. The word bit comes from binary digit: Binary digit = bit Every time the computer “reads” an instruction, it translates that instruction into a series of bits (0’s and 1’s). In most computers every letter, number, and symbol is translated into eight bits, a combination of eight 0’s and 1’s. For example the letter A is translated into 01000001. The letter B is 01000010. Every single keystroke on the keyboard translates into a different combination of eight bits. A group of eight bits is called a byte. Therefore, a byte is a combination of eight 0’s and 1’s. Eight bits = 1 byte Capacity of computer memory, storage such as USB devices, DVD’s are measured in bytes. For example a Word file might be 35 KB while a picture taken by a digital camera might be 4.5 MG. Hard drives normally are measured in GB or TB: Kilobyte (KB) approximately 1,000 bytes MegaByte (MB) approximately 1,000,000 (million) bytes Gigabtye (GB) approximately 1,000,000,000 (billion) bytes Terabyte (TB) approximately 1,000,000,000,000 (trillion) bytes The binary code that computers use is called the ASCII (American Standard Code for Information Interchange) code.
    [Show full text]
  • Subtyping Recursive Types
    ACM Transactions on Programming Languages and Systems, 15(4), pp. 575-631, 1993. Subtyping Recursive Types Roberto M. Amadio1 Luca Cardelli CNRS-CRIN, Nancy DEC, Systems Research Center Abstract We investigate the interactions of subtyping and recursive types, in a simply typed λ-calculus. The two fundamental questions here are whether two (recursive) types are in the subtype relation, and whether a term has a type. To address the first question, we relate various definitions of type equivalence and subtyping that are induced by a model, an ordering on infinite trees, an algorithm, and a set of type rules. We show soundness and completeness between the rules, the algorithm, and the tree semantics. We also prove soundness and a restricted form of completeness for the model. To address the second question, we show that to every pair of types in the subtype relation we can associate a term whose denotation is the uniquely determined coercion map between the two types. Moreover, we derive an algorithm that, when given a term with implicit coercions, can infer its least type whenever possible. 1This author's work has been supported in part by Digital Equipment Corporation and in part by the Stanford-CNR Collaboration Project. Page 1 Contents 1. Introduction 1.1 Types 1.2 Subtypes 1.3 Equality of Recursive Types 1.4 Subtyping of Recursive Types 1.5 Algorithm outline 1.6 Formal development 2. A Simply Typed λ-calculus with Recursive Types 2.1 Types 2.2 Terms 2.3 Equations 3. Tree Ordering 3.1 Subtyping Non-recursive Types 3.2 Folding and Unfolding 3.3 Tree Expansion 3.4 Finite Approximations 4.
    [Show full text]
  • IEEE Standard 754 for Binary Floating-Point Arithmetic
    Work in Progress: Lecture Notes on the Status of IEEE 754 October 1, 1997 3:36 am Lecture Notes on the Status of IEEE Standard 754 for Binary Floating-Point Arithmetic Prof. W. Kahan Elect. Eng. & Computer Science University of California Berkeley CA 94720-1776 Introduction: Twenty years ago anarchy threatened floating-point arithmetic. Over a dozen commercially significant arithmetics boasted diverse wordsizes, precisions, rounding procedures and over/underflow behaviors, and more were in the works. “Portable” software intended to reconcile that numerical diversity had become unbearably costly to develop. Thirteen years ago, when IEEE 754 became official, major microprocessor manufacturers had already adopted it despite the challenge it posed to implementors. With unprecedented altruism, hardware designers had risen to its challenge in the belief that they would ease and encourage a vast burgeoning of numerical software. They did succeed to a considerable extent. Anyway, rounding anomalies that preoccupied all of us in the 1970s afflict only CRAY X-MPs — J90s now. Now atrophy threatens features of IEEE 754 caught in a vicious circle: Those features lack support in programming languages and compilers, so those features are mishandled and/or practically unusable, so those features are little known and less in demand, and so those features lack support in programming languages and compilers. To help break that circle, those features are discussed in these notes under the following headings: Representable Numbers, Normal and Subnormal, Infinite
    [Show full text]
  • A Variable Precision Hardware Acceleration for Scientific Computing Andrea Bocco
    A variable precision hardware acceleration for scientific computing Andrea Bocco To cite this version: Andrea Bocco. A variable precision hardware acceleration for scientific computing. Discrete Mathe- matics [cs.DM]. Université de Lyon, 2020. English. NNT : 2020LYSEI065. tel-03102749 HAL Id: tel-03102749 https://tel.archives-ouvertes.fr/tel-03102749 Submitted on 7 Jan 2021 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. N°d’ordre NNT : 2020LYSEI065 THÈSE de DOCTORAT DE L’UNIVERSITÉ DE LYON Opérée au sein de : CEA Grenoble Ecole Doctorale InfoMaths EDA N17° 512 (Informatique Mathématique) Spécialité de doctorat :Informatique Soutenue publiquement le 29/07/2020, par : Andrea Bocco A variable precision hardware acceleration for scientific computing Devant le jury composé de : Frédéric Pétrot Président et Rapporteur Professeur des Universités, TIMA, Grenoble, France Marc Dumas Rapporteur Professeur des Universités, École Normale Supérieure de Lyon, France Nathalie Revol Examinatrice Docteure, École Normale Supérieure de Lyon, France Fabrizio Ferrandi Examinateur Professeur associé, Politecnico di Milano, Italie Florent de Dinechin Directeur de thèse Professeur des Universités, INSA Lyon, France Yves Durand Co-directeur de thèse Docteur, CEA Grenoble, France Cette thèse est accessible à l'adresse : http://theses.insa-lyon.fr/publication/2020LYSEI065/these.pdf © [A.
    [Show full text]
  • Numerical Computing with IEEE Floating Point Arithmetic This Page Intentionally Left Blank Numerical Computing with IEEE Floating Point Arithmetic
    Numerical Computing with IEEE Floating Point Arithmetic This page intentionally left blank Numerical Computing with IEEE Floating Point Arithmetic Including One Theorem, One Rule of Thumb, and One Hundred and One Exercises Michael L. Overton Courant Institute of Mathematical Sciences New York University New York, New York siam. Society for Industrial and Applied Mathematics Philadelphia Copyright © 2001 by the Society for Industrial and Applied Mathematics. 1098765432 All rights reserved. Printed in the United States of America. No part of this book may be reproduced, stored, or transmitted in any manner without the written permission of the publisher. For information, write to the Society for Industrial and Applied Mathematics, 3600 University City Science Center, Philadelphia, PA 19104-2688. Library of Congress Cataloging-in-Publication Data Overton, Michael L Numerical computing with IEEE floating point arithmetic / Michael L Overton. p. cm. Includes bibliographical references and index. ISBN 0-89871-571-7 I. Computer arithmetic. 2. Floating-point arithmetic. 3. Numerical calculations. I. Title. QA76.9.M35O94200I O04'.0l'5l--dc2l 00-067941 SlcLJTL is a registered trademark. Dedicated to girls who like math especially my daughter Eleuthera Overton Sa This page intentionally left blank Contents Preface ix Acknowledgments xi 1 Introduction 1 2 The Real Numbers 5 3 Computer Representation of Numbers 9 4 IEEE Floating Point Representation 17 5 Rounding 25 6 Correctly Rounded Floating Point Operations 31 7 Exceptions 41 8 The Intel Microprocessors 49 9 Programming Languages 55 10 Floating Point in C 59 11 Cancellation 71 12 Conditioning of Problems 77 13 Stability of Algorithms 83 14 Conclusion 97 Bibliography 101 vii This page intentionally left blank Preface Numerical computing is a vital part of the modern scientific infrastructure.
    [Show full text]
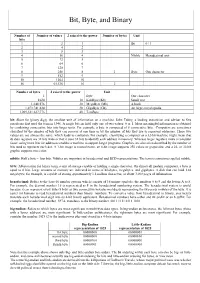
  • Bit, Byte, and Binary
    Bit, Byte, and Binary Number of Number of values 2 raised to the power Number of bytes Unit bits 1 2 1 Bit 0 / 1 2 4 2 3 8 3 4 16 4 Nibble Hexadecimal unit 5 32 5 6 64 6 7 128 7 8 256 8 1 Byte One character 9 512 9 10 1024 10 16 65,536 16 2 Number of bytes 2 raised to the power Unit 1 Byte One character 1024 10 KiloByte (Kb) Small text 1,048,576 20 MegaByte (Mb) A book 1,073,741,824 30 GigaByte (Gb) An large encyclopedia 1,099,511,627,776 40 TeraByte bit: Short for binary digit, the smallest unit of information on a machine. John Tukey, a leading statistician and adviser to five presidents first used the term in 1946. A single bit can hold only one of two values: 0 or 1. More meaningful information is obtained by combining consecutive bits into larger units. For example, a byte is composed of 8 consecutive bits. Computers are sometimes classified by the number of bits they can process at one time or by the number of bits they use to represent addresses. These two values are not always the same, which leads to confusion. For example, classifying a computer as a 32-bit machine might mean that its data registers are 32 bits wide or that it uses 32 bits to identify each address in memory. Whereas larger registers make a computer faster, using more bits for addresses enables a machine to support larger programs.
    [Show full text]
  • MIPS Floating Point
    CS352H: Computer Systems Architecture Lecture 6: MIPS Floating Point September 17, 2009 University of Texas at Austin CS352H - Computer Systems Architecture Fall 2009 Don Fussell Floating Point Representation for dynamically rescalable numbers Including very small and very large numbers, non-integers Like scientific notation –2.34 × 1056 +0.002 × 10–4 normalized +987.02 × 109 not normalized In binary yyyy ±1.xxxxxxx2 × 2 Types float and double in C University of Texas at Austin CS352H - Computer Systems Architecture Fall 2009 Don Fussell 2 Floating Point Standard Defined by IEEE Std 754-1985 Developed in response to divergence of representations Portability issues for scientific code Now almost universally adopted Two representations Single precision (32-bit) Double precision (64-bit) University of Texas at Austin CS352H - Computer Systems Architecture Fall 2009 Don Fussell 3 IEEE Floating-Point Format single: 8 bits single: 23 bits double: 11 bits double: 52 bits S Exponent Fraction x = (!1)S "(1+Fraction)"2(Exponent!Bias) S: sign bit (0 ⇒ non-negative, 1 ⇒ negative) Normalize significand: 1.0 ≤ |significand| < 2.0 Always has a leading pre-binary-point 1 bit, so no need to represent it explicitly (hidden bit) Significand is Fraction with the “1.” restored Exponent: excess representation: actual exponent + Bias Ensures exponent is unsigned Single: Bias = 127; Double: Bias = 1203 University of Texas at Austin CS352H - Computer Systems Architecture Fall 2009 Don Fussell 4 Single-Precision Range Exponents 00000000 and 11111111 reserved Smallest
    [Show full text]