DOCSLIB.ORG

Chapter 10 Measuring the Stars

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Chapter 10 Measuring the Stars Chapter 10 Measuring the Stars Read material in Chapter 10 Some of the topics included in this chapter • Stellar parallax • Distance to the stars • Stellar motion • Luminosity and apparent brightness of stars • The magnitude scale • Stellar temperatures • Stellar spectra • Spectral classification • Stellar sizes • The Herzsprung-Russell (HR)diagram • The main sequence • Spectroscopic parallax • Extending the cosmic distance • Luminosity class • Stellar masses Parallax is the apparent shift of an object relative to some distant background as the observer’s point of view changes It is the only direct way to measure distances to stars . It makes use Earth’s orbit as baseline . Parallactic angle = 1/2 angular shift .A new unit of distance: Parsec . By definition, parsec (pc) is the distance from the Sun to a star that has a parallax of 1” (1 arc second) Parallax Formula: . Distance (in pc) = 1/parallax (in arcsec) . One parsec = 206,265 AU or ~3.3 light-years As the distance increases to a star, the parallax decreases…. Examples using the parallax formula: If the measured parallax is 1 arcsec, then the distance of the star is 1 pc. (Distance 1 pc = 1/1 arcsec) If the measured parallax is 0.5 arcsec, then the distance of the star is 2 pc. (Distance 2 pc = 1/0.5 arcsec) Note: 1 parsec = 3.26 light-years. The Solar Neighborhood Let’s get to know our neighborhood: A plot of the 30 closest stars within 4 parsecs (~ 13 ly) from the Sun. The gridlines are distances in the galactic plane (the plane of the disc of the Milky Way) The Nearest Stars More examples using the parallax formula The nearest star Proxima Centauri (the faintest star of the triple star system Alpha Centauri) has a parallax of 0.76 arcsec. • Therefore, distance = 1 / 0.76 = 1.32 pc (4.29 ly) • The next nearest star is Barnard’s star, with a parallax of 0.55” • Therefore, d = 1 / 0.55 = 1.82 pc (5.93 ly) • From the ground, we can measure parallactic angles of ~1/30 (0.03”) arcsec, corresponding to distances out to ~30 pc (96 ly). • There are several thousand stars within that distance from the Sun. • From space (Hipparcos satellite), parallax’s can be measured down to about 5/1000 arcsec, which corresponds to 200 pc (~660 ly). • There are several million stars within that distance. Using the stellar parallax, the distance to these stars can be determined directly Stellar Proper Motion • Parallax is an apparent motion of stars due to Earth orbiting the Sun. • But stars do have real space motions. • Space motion has two components: 1) “line-of-sight” or radial motion (measured through Doppler shift of emission/absorption lines) 2) “transverse” motion (perpendicular to the line of sight) observer star radial motion transverse space motion How to determine the two component of the space motion of a star? • Use the Doppler shift to determine the radial component. Observe the shift in wavelengths of the emission or absorption lines. Then apply the formula of Doppler shift to determine the radial velocity • Use the proper motion and the distance to determine the transverse component. First we need to measure the proper motion. Proper motion is measured in arc seconds/year. Then we need to know the distance to the star using parallax so we can determine the transverse component • Finally use trigonometry to calculate the transverse velocity • This method works for stars that are nearby so we can measure the proper motion. • The total velocity can be calculated using the Pythagorean theorem: ____________________________________ Total velocity = √ [(Radial velocity)² + (Transverse velocity)²] Stellar Proper Motion: Barnard’s Star • Two pictures, taken 22 years apart ( Taken at the same time of the year so it doesn’t show parallax!). Barnard’s star is a red dwarf of magnitude +9.5, invisible to the naked eye (limit of naked eye is +6) • Barnard’s star has a proper motion of 10.3 arcsec/year (it is the star with the largest proper motion) • Given d = 1.8 pc, this proper motion corresponds to a “transverse” velocity of ~90 km/s ! Question: What does the proper motion depend on? Answer 1: Space velocity Answer 2: Distance Some important definitions and concepts • Luminosity is the amount of radiation leaving a star per unit time. • Luminosity is an intrinsic property of a star. • It is also referred as the star absolute brightness. It doesn’t depend on the distance or motion of the observer respect to the star. • Apparent brightness or Flux. When we observe a star we see its apparent brightness, not its luminosity. The apparent brightness (or flux) is the amount of light striking the unit area of some light sensitive device such as the human eye or a CCD. It depends on the distance to the star. Apparent Brightness and the Inverse Square Law: Proportional to 1/d2 • Light “spreads out” like the distance squared. • Through a sphere twice as large, the light energy is spread out over four times the area. (area of sphere = 4d2) The apparent brightness or Flux decreases with distance, it is inversely proportional to the square of the distance. It can be determined by: Luminosity Flux = 4d2 To know a star’s luminosity we must measure its apparent brightness (or flux) and know its distance. Then, Luminosity = Flux *4d2 Luminosity and Apparent Brightness Two stars A and B of different luminosity can appear equality bright to an observer if the brightest star B is more distant than the fainter star A The Magnitude Scale 2nd century BC, Hipparchus ranked all visible stars Faintest He assigned to the brightest star a magnitude 1, and to the faintest a magnitude 6. Later, astronomer found out that a difference of 5 magnitudes from 1 (brightest) to 6 (faintest) correspond to a change in brightness of 100 To our eyes, a change of one magnitude = a factor of 2.512 in flux or brightness. The magnitude scale is logarithmic. Each magnitude corresponds to a factor of 1001/5 2.5 5 magnitudes = factor 100 in brightness. The apparent magnitude scale was later Brightest extended to negative values for brighter objects and to larger positive values for fainter objects Equivalence between magnitude and brightness Magnitude Brightness -1 2.512 0 2.512 1 2.512 2 2.512 3 2.512 4 2.512 5 2.512 6 The change of brightness between magnitude 1 and 6 is 2.512^5 = 100 In general, the difference in brightness between two magnitudes is: Difference in brightness = 2.512 ^n, where n is the difference in magnitude Example: What is the difference in brightness between magnitude -1 and +1? Answer: n=2, difference in brightness = 2.512² = 2.512 x 2.512 = 6.31 Absolute Magnitude is the apparent magnitude of a star as measured from a distance of 10 pc (33 ly). Sun’s absolute magnitude = +4.8 It is the magnitude of the Sun if it is placed at a distance of 10 pc. Just slightly brighter than the faintest stars visible to the naked eye (magnitude = +6) in the sky. Enhanced color picture of the sky Notice the color differences among the stars Stellar Temperature: Spectra • The spectra shows 7 stars with same chemical composition but different temperatures. • Different spectra result from different temperatures. Example: Hydrogen absorption lines are relatively weak in the hottest star because it is mostly ionized. Conversely, hotter temperatures are needed to excite and ionize Helium so these lines are strongest in the hottest star. Molecular absorption lines (TiO) are present in low temperature stars. The low temperatures allow formation of molecules Ti Titanium, TiO titanium oxide Spectral Classification: A classification of stars was started by the “Pickering’s women”, a group of women hired by the director of the Harvard College observatory, including Annie Cannon Annie Jump Cannon The stars were classified by the Hydrogen line strength, and started as A, B, C, D, … But after a while they realized that there is a sequence in temperature so they rearranged the letters (some letters were drop from the classification) so that it reflect a sequence in temperature. It became: O, B, A, F, G, K, M, (L) A temperature sequence! Cannon’s spectral classification system was officially adopted in 1910. Spectral Classification A mnemonic to remember the correct order: “Oh Be A Fine Girl/Guy Kiss Me” Each letter is divided in 10 smaller subdivisions from 0 to 9. The lower the number, the hotter the star. Example, G0 (hotter) to G9 (cooler). The Sun is classified as a G2 star, the surface temperature is 5800 K Strengths of Lines at Each Spectral Type Stellar Radii • Almost all stars are so distant that the image of their discs look so small. Their images appear only as an unresolved point of light even in the largest telescopes. Actually the image shows the Airy disk produced by the star. • A small number of stars are big, bright and close enough to determine their sizes directly through geometry. •Knowing the angular diameter and the distance to the star, it is possible to use geometry to calculate its size. Diameter/2π x distance = Angular diameter/360 Stellar Radii • One example in which it is possible to use geometry to determine the radius is the star Betelgeuse in the Orion constellation • The star is a red giant located about 640 ly from Earth • Betelgeuse size is about 600 time larger than the Sun • Its photosphere exceed the size of the orbit of Mars • Using the Hubble telescope it is possible to resolve its atmosphere and measure its diameter directly • The measured angular size is about 0.043-0.056 arc seconds An indirect way to determine the stars radii • Most of the stars are too distant or too small to allow the direct determination of their size.
Load more

Recommended publications
  • Astronomy, Astrophysics, and Cosmology
    Astronomy, Astrophysics, and Cosmology Luis A. Anchordoqui Department of Physics and Astronomy Lehman College, City University of New York Lesson I February 2, 2016 arXiv:0706.1988 L. A. Anchordoqui (CUNY) Astronomy, Astrophysics, and Cosmology 2-2-2016 1 / 22 Table of Contents 1 Stars and Galaxies 2 Distance Measurements Stellar parallax Stellar luminosity L. A. Anchordoqui (CUNY) Astronomy, Astrophysics, and Cosmology 2-2-2016 2 / 22 Stars and Galaxies Night sky provides a strong impression of a changeless universe G Clouds drift across the Moon + on longer times Moon itself grows and shrinks G Moon and planets move against the background of stars G These are merely local phenomena caused by motions within our solar system G Far beyond planets + stars appear motionless L. A. Anchordoqui (CUNY) Astronomy, Astrophysics, and Cosmology 2-2-2016 3 / 22 Stars and Galaxies According to ancient cosmological belief + stars except for a few that appeared to move (the planets) where fixed on sphere beyond last planet The universe was self contained and we (here on Earth) were at its center L. A. Anchordoqui (CUNY) Astronomy, Astrophysics, and Cosmology 2-2-2016 4 / 22 Stars and Galaxies Our view of universe dramatically changed after Galileo’s telescopic observations: we no longer place ourselves at the center and we view the universe as vastly larger L. A. Anchordoqui (CUNY) Astronomy, Astrophysics, and Cosmology 2-2-2016 5 / 22 Stars and Galaxies Is the Earth flat? L. A. Anchordoqui (CUNY) Astronomy, Astrophysics, and Cosmology 2-2-2016 6 / 22 Stars and Galaxies Distances involved are so large that we specify them in terms of the time it takes the light to travel a given distance light second + 1 ls = 1 s 3 108 m/s = 3 108m = 300, 000 km × × light minute + 1 lm = 18 106 km × light year + 1 ly = 2.998 108 m/s 3.156 107 s/yr × · × = 9.46 1015 m 1013 km × ≈ How long would it take the space shuttle to go 1 ly? Shuttle orbits Earth @ 18,000 mph + it would need 37, 200 yr L.
    [Show full text]
  • Binocular Universe: Sly Fox September 2010 Phil Harrington
    Binocular Universe is available every month on Cloudynights.com Binocular Universe: Sly Fox September 2010 Phil Harrington ast month's Stellafane convention, held atop Breezy Hill outside of Springfield, Vermont, was the best in recent memory. The skies were the Lclearest we've had in years, giving us a chance to enjoy the beauty of the summer Milky Way, which stretched from horizon to horizon. Armed with my trusty 10x50 and 16x70 binoculars, I sat back in my reclining chair and swept the plane of our Galaxy in pursuit of some old friends and new conquests. Above: Summer star map from Star Watch by Phil Harrington Binocular Universe is available every month on Cloudynights.com Above: Finder chart for this month's Binocular Universe. Chart adapted from Touring the Universe through Binoculars Atlas (TUBA), www.philharrington.net/tuba.htm Binocular Universe is available every month on Cloudynights.com Here are a few gems I bumped into along the way as I viewed the tiny constellation of Vulpecula the Fox. Vulpecula is a faint summertime constellation wedged between Cygnus (the Swan) to the north and Sagitta (the Arrow) to the south. None of Vulpecula’s stars shine brighter than magnitude 4.5, so seeing a fox here is a tall order indeed. But the sly Fox holds many binocular treasures for those who the time to seek them out. Vulpecula was created in 1687 by the Polish astronomer Johannes Hevelius. His original drawing showed a small fox carrying a hapless goose in its mouth. He called the combination Vulpecula et Anser ("the little fox and the goose").
    [Show full text]
  • A Hot Subdwarf-White Dwarf Super-Chandrasekhar Candidate
    A hot subdwarf–white dwarf super-Chandrasekhar candidate supernova Ia progenitor Ingrid Pelisoli1,2*, P. Neunteufel3, S. Geier1, T. Kupfer4,5, U. Heber6, A. Irrgang6, D. Schneider6, A. Bastian1, J. van Roestel7, V. Schaffenroth1, and B. N. Barlow8 1Institut fur¨ Physik und Astronomie, Universitat¨ Potsdam, Haus 28, Karl-Liebknecht-Str. 24/25, D-14476 Potsdam-Golm, Germany 2Department of Physics, University of Warwick, Coventry, CV4 7AL, UK 3Max Planck Institut fur¨ Astrophysik, Karl-Schwarzschild-Straße 1, 85748 Garching bei Munchen¨ 4Kavli Institute for Theoretical Physics, University of California, Santa Barbara, CA 93106, USA 5Texas Tech University, Department of Physics & Astronomy, Box 41051, 79409, Lubbock, TX, USA 6Dr. Karl Remeis-Observatory & ECAP, Astronomical Institute, Friedrich-Alexander University Erlangen-Nuremberg (FAU), Sternwartstr. 7, 96049 Bamberg, Germany 7Division of Physics, Mathematics and Astronomy, California Institute of Technology, Pasadena, CA 91125, USA 8Department of Physics and Astronomy, High Point University, High Point, NC 27268, USA *[email protected] ABSTRACT Supernova Ia are bright explosive events that can be used to estimate cosmological distances, allowing us to study the expansion of the Universe. They are understood to result from a thermonuclear detonation in a white dwarf that formed from the exhausted core of a star more massive than the Sun. However, the possible progenitor channels leading to an explosion are a long-standing debate, limiting the precision and accuracy of supernova Ia as distance indicators. Here we present HD 265435, a binary system with an orbital period of less than a hundred minutes, consisting of a white dwarf and a hot subdwarf — a stripped core-helium burning star.
    [Show full text]
  • Solar Radius Determined from PICARD/SODISM Observations and Extremely Weak Wavelength Dependence in the Visible and the Near-Infrared
    A&A 616, A64 (2018) https://doi.org/10.1051/0004-6361/201832159 Astronomy c ESO 2018 & Astrophysics Solar radius determined from PICARD/SODISM observations and extremely weak wavelength dependence in the visible and the near-infrared M. Meftah1, T. Corbard2, A. Hauchecorne1, F. Morand2, R. Ikhlef2, B. Chauvineau2, C. Renaud2, A. Sarkissian1, and L. Damé1 1 Université Paris Saclay, Sorbonne Université, UVSQ, CNRS, LATMOS, 11 Boulevard d’Alembert, 78280 Guyancourt, France e-mail: [email protected] 2 Université de la Côte d’Azur, Observatoire de la Côte d’Azur (OCA), CNRS, Boulevard de l’Observatoire, 06304 Nice, France Received 23 October 2017 / Accepted 9 May 2018 ABSTRACT Context. In 2015, the International Astronomical Union (IAU) passed Resolution B3, which defined a set of nominal conversion constants for stellar and planetary astronomy. Resolution B3 defined a new value of the nominal solar radius (RN = 695 700 km) that is different from the canonical value used until now (695 990 km). The nominal solar radius is consistent with helioseismic estimates. Recent results obtained from ground-based instruments, balloon flights, or space-based instruments highlight solar radius values that are significantly different. These results are related to the direct measurements of the photospheric solar radius, which are mainly based on the inflection point position methods. The discrepancy between the seismic radius and the photospheric solar radius can be explained by the difference between the height at disk center and the inflection point of the intensity profile on the solar limb. At 535.7 nm (photosphere), there may be a difference of 330 km between the two definitions of the solar radius.
    [Show full text]
  • 2. Astrophysical Constants and Parameters
    2. Astrophysical constants 1 2. ASTROPHYSICAL CONSTANTS AND PARAMETERS Table 2.1. Revised May 2010 by E. Bergren and D.E. Groom (LBNL). The figures in parentheses after some values give the one standard deviation uncertainties in the last digit(s). Physical constants are from Ref. 1. While every effort has been made to obtain the most accurate current values of the listed quantities, the table does not represent a critical review or adjustment of the constants, and is not intended as a primary reference. The values and uncertainties for the cosmological parameters depend on the exact data sets, priors, and basis parameters used in the fit. Many of the parameters reported in this table are derived parameters or have non-Gaussian likelihoods. The quoted errors may be highly correlated with those of other parameters, so care must be taken in propagating them. Unless otherwise specified, cosmological parameters are best fits of a spatially-flat ΛCDM cosmology with a power-law initial spectrum to 5-year WMAP data alone [2]. For more information see Ref. 3 and the original papers. Quantity Symbol, equation Value Reference, footnote speed of light c 299 792 458 m s−1 exact[4] −11 3 −1 −2 Newtonian gravitational constant GN 6.674 3(7) × 10 m kg s [1] 19 2 Planck mass c/GN 1.220 89(6) × 10 GeV/c [1] −8 =2.176 44(11) × 10 kg 3 −35 Planck length GN /c 1.616 25(8) × 10 m[1] −2 2 standard gravitational acceleration gN 9.806 65 m s ≈ π exact[1] jansky (flux density) Jy 10−26 Wm−2 Hz−1 definition tropical year (equinox to equinox) (2011) yr 31 556 925.2s≈ π × 107 s[5] sidereal year (fixed star to fixed star) (2011) 31 558 149.8s≈ π × 107 s[5] mean sidereal day (2011) (time between vernal equinox transits) 23h 56m 04.s090 53 [5] astronomical unit au, A 149 597 870 700(3) m [6] parsec (1 au/1 arc sec) pc 3.085 677 6 × 1016 m = 3.262 ...ly [7] light year (deprecated unit) ly 0.306 6 ..
    [Show full text]
  • 190 6Ap J 23. . 2 4 8C the LUMINOSITY of the BRIGHTEST
    8C 4 2 . 23. J 6Ap 190 THE LUMINOSITY OF THE BRIGHTEST STARS By GEORGE C. COMSTOCK The prevailing opinion among astronomers admits the presence in the heavens of at least a few stars of extraordinary intrinsic bril- liancy. ‘ Gill, Kapteyn, and Newcomb have under differing forms announced the probable existence of stars having a luminosity exceeding that of the Sun by ten-thousand fold or more, possibly a hundred-thousand fold, and Canopus is cited as an example of such a star. It is the purpose of the present article to examine the evidence upon which this doctrine is based, and the extent to which that evidence is confirmed or refuted by other considerations. As respects Canopus, the case is presented by Gill, Researches on Stellar Parallax, substantially as follows. The measured par- allaxes of this star and of a Centauri are respectively ofoio and 0^762, and their stellar magnitudes are — 0.96 and+ 0.40; i. e., Canopus is 3.50 times brighter than a Centauri. The light of the one star, is therefore 3.50 times as great as that of the other. But since a Centauri has the same mass and the same spectrum as the Sun, and therefore presumably emits the same quantity of light, we may substitute the Sun in place of a Centauri in this com- parison, and find from the expression given above that Canopus is more than 20,000 times as bright as the Sun. I have sought for other cases of a similar character, using a method slightly different from that of Gill.
    [Show full text]
  • Apparent and Absolute Magnitudes of Stars: a Simple Formula
    Available online at www.worldscientificnews.com WSN 96 (2018) 120-133 EISSN 2392-2192 Apparent and Absolute Magnitudes of Stars: A Simple Formula Dulli Chandra Agrawal Department of Farm Engineering, Institute of Agricultural Sciences, Banaras Hindu University, Varanasi - 221005, India E-mail address: [email protected] ABSTRACT An empirical formula for estimating the apparent and absolute magnitudes of stars in terms of the parameters radius, distance and temperature is proposed for the first time for the benefit of the students. This reproduces successfully not only the magnitudes of solo stars having spherical shape and uniform photosphere temperature but the corresponding Hertzsprung-Russell plot demonstrates the main sequence, giants, super-giants and white dwarf classification also. Keywords: Stars, apparent magnitude, absolute magnitude, empirical formula, Hertzsprung-Russell diagram 1. INTRODUCTION The visible brightness of a star is expressed in terms of its apparent magnitude [1] as well as absolute magnitude [2]; the absolute magnitude is in fact the apparent magnitude while it is observed from a distance of . The apparent magnitude of a celestial object having flux in the visible band is expressed as [1, 3, 4] ( ) (1) ( Received 14 March 2018; Accepted 31 March 2018; Date of Publication 01 April 2018 ) World Scientific News 96 (2018) 120-133 Here is the reference luminous flux per unit area in the same band such as that of star Vega having apparent magnitude almost zero. Here the flux is the magnitude of starlight the Earth intercepts in a direction normal to the incidence over an area of one square meter. The condition that the Earth intercepts in the direction normal to the incidence is normally fulfilled for stars which are far away from the Earth.
    [Show full text]
  • The Extragalactic Distance Scale
    The Extragalactic Distance Scale Published in "Stellar astrophysics for the local group" : VIII Canary Islands Winter School of Astrophysics. Edited by A. Aparicio, A. Herrero, and F. Sanchez. Cambridge ; New York : Cambridge University Press, 1998 Calibration of the Extragalactic Distance Scale By BARRY F. MADORE1, WENDY L. FREEDMAN2 1NASA/IPAC Extragalactic Database, Infrared Processing & Analysis Center, California Institute of Technology, Jet Propulsion Laboratory, Pasadena, CA 91125, USA 2Observatories, Carnegie Institution of Washington, 813 Santa Barbara St., Pasadena CA 91101, USA The calibration and use of Cepheids as primary distance indicators is reviewed in the context of the extragalactic distance scale. Comparison is made with the independently calibrated Population II distance scale and found to be consistent at the 10% level. The combined use of ground-based facilities and the Hubble Space Telescope now allow for the application of the Cepheid Period-Luminosity relation out to distances in excess of 20 Mpc. Calibration of secondary distance indicators and the direct determination of distances to galaxies in the field as well as in the Virgo and Fornax clusters allows for multiple paths to the determination of the absolute rate of the expansion of the Universe parameterized by the Hubble constant. At this point in the reduction and analysis of Key Project galaxies H0 = 72km/ sec/Mpc ± 2 (random) ± 12 [systematic]. Table of Contents INTRODUCTION TO THE LECTURES CEPHEIDS BRIEF SUMMARY OF THE OBSERVED PROPERTIES OF CEPHEID
    [Show full text]
  • Lecture 5: Stellar Distances 10/2/19, 802 AM
    Lecture 5: Stellar Distances 10/2/19, 802 AM Astronomy 162: Introduction to Stars, Galaxies, & the Universe Prof. Richard Pogge, MTWThF 9:30 Lecture 5: Distances of the Stars Readings: Ch 19, section 19-1 Key Ideas Distance is the most important & most difficult quantity to measure in Astronomy Method of Trigonometric Parallaxes Direct geometric method of finding distances Units of Cosmic Distance: Light Year Parsec (Parallax second) Why are Distances Important? Distances are necessary for estimating: Total energy emitted by an object (Luminosity) Masses of objects from their orbital motions True motions through space of stars Physical sizes of objects The problem is that distances are very hard to measure... The problem of measuring distances Question: How do you measure the distance of something that is beyond the reach of your measuring instruments? http://www.astronomy.ohio-state.edu/~pogge/Ast162/Unit1/distances.html Page 1 of 7 Lecture 5: Stellar Distances 10/2/19, 802 AM Examples of such problems: Large-scale surveying & mapping problems. Military range finding to targets Measuring distances to any astronomical object Answer: You resort to using GEOMETRY to find the distance. The Method of Trigonometric Parallaxes Nearby stars appear to move with respect to more distant background stars due to the motion of the Earth around the Sun. This apparent motion (it is not "true" motion) is called Stellar Parallax. (Click on the image to view at full scale [Size: 177Kb]) In the picture above, the line of sight to the star in December is different than that in June, when the Earth is on the other side of its orbit.
    [Show full text]
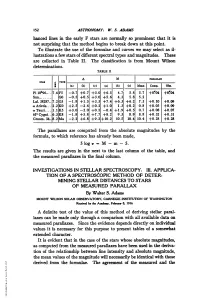
  • Not Surprising That the Method Begins to Break Down at This Point
    152 ASTRONOMY: W. S. ADAMS hanced lines in the early F stars are normally so prominent that it is not surprising that the method begins to break down at this point. To illustrate the use of the formulae and curves we may select as il- lustrations a few stars of different spectral types and magnitudes. These are collected in Table II. The classification is from Mount Wilson determinations. TABLE H ~A M PARAIuAX srTATYP_________________ (a) I(b) (C) (a) (b) c) Mean Comp. Ob. Pi 10U96.... 7.6F5 -0.7 +0.7 +3.0 +6.5 4.7 5.8 5.7 +0#04 +0.04 Sun........ GO -0.5 +0.5 +3.0 +5.6 4.3 5.8 5.2 Lal. 38287.. 7.2 G5 -1.8 +1.5 +3.5 +7.4 +6.3 +6.2 7.3 +0.10 +0.09 a Arietis... 2.2K0O +2.5 -2.4 +0.2 +1.0 1.3 +0.2 0.8 +0.05 +0.09 aTauri.... 1.1K5 +3.0 -2.0 +0.5 -0.4 +1.9 +0.5 0.7 +0.08 +0.07 61' Cygni...6.3K8 -1.8 +5.8 +7.7 +8.2 9.3 8.9 8.8 +0.32 +0.31 Groom. 34..8.2 Ma -2.2 +6.8 +9.2 +10.2 10.5 10.4 10.4 +0.28 +0.28 The parallaxes are computed from the absolute magnitudes by the formula, to which reference has already been made, 5 logr = M - m - 5. The results are given in the next to the last column of the table, and the measured parallaxes in the final column.
    [Show full text]
  • Spectroscopy of Variable Stars
    Spectroscopy of Variable Stars Steve B. Howell and Travis A. Rector The National Optical Astronomy Observatory 950 N. Cherry Ave. Tucson, AZ 85719 USA Introduction A Note from the Authors The goal of this project is to determine the physical characteristics of variable stars (e.g., temperature, radius and luminosity) by analyzing spectra and photometric observations that span several years. The project was originally developed as a The 2.1-meter telescope and research project for teachers participating in the NOAO TLRBSE program. Coudé Feed spectrograph at Kitt Peak National Observatory in Ari- Please note that it is assumed that the instructor and students are familiar with the zona. The 2.1-meter telescope is concepts of photometry and spectroscopy as it is used in astronomy, as well as inside the white dome. The Coudé stellar classification and stellar evolution. This document is an incomplete source Feed spectrograph is in the right of information on these topics, so further study is encouraged. In particular, the half of the building. It also uses “Stellar Spectroscopy” document will be useful for learning how to analyze the the white tower on the right. spectrum of a star. Prerequisites To be able to do this research project, students should have a basic understanding of the following concepts: • Spectroscopy and photometry in astronomy • Stellar evolution • Stellar classification • Inverse-square law and Stefan’s law The control room for the Coudé Description of the Data Feed spectrograph. The spec- trograph is operated by the two The spectra used in this project were obtained with the Coudé Feed telescopes computers on the left.
    [Show full text]
  • Jason A. Dittmann 51 Pegasi B Postdoctoral Fellow
    Jason A. Dittmann 51 Pegasi b Postdoctoral Fellow Contact Massachusetts Institute of Technology MIT Kavli Institute: 37-438f 617-258-5928 (office) 70 Vassar St. 520-820-0928 (cell) Cambridge, MA 02139 [email protected] Education Harvard University, Cambridge, MA PhD, Astronomy and Astrophysics, May 2016 Advisor: David Charbonneau, PhD • University of Arizona, Tucson, AZ BS, Astronomy, Physics, May 2010 Advisor: Laird Close, PhD • Recent 51 Pegasi b Postdoctoral Fellow July 2017 – Present Research Earth and Planetary Science Department, MIT Positions Faculty Contact: Sara Seager Postdoctoral Researcher Feb 2017 – June 2017 Kavli Institute, MIT Supervisor: Sarah Ballard Postdoctoral Researcher July 2016 – Jan 2017 Center for Astrophysics, Harvard University Supervisor: David Charbonneau Research Assistant Sep 2010 – May 2016 Center for Astrophysics, Harvard University Advisors: David Charbonneau Publication 16 first and second authored publications Summary 22 additional co-authored publications 1 first-authored publication in Nature 1 co-authored publication in Nature Selected 51 Pegasi b Postdoctoral Fellowship 2017 – Present Awards and Pierce Fellowship 2010 – 2013 Honors Certificate of Distinction in Teaching 2012 Best Project Award, Physics Ugrd. Research Symp. 2009 Best Undergraduate Research (Steward Observatory) 2009 – 2010 Grants Principal Investigator, Hubble Space Telescope 2017, 10 orbits Awarded “Initial Reconaissance of a Transiting Rocky (maximum award) Planet in a Nearby M-Dwarf’s Habitable Zone” Principal Investigator,
    [Show full text]