DOCSLIB.ORG

A New Trajectory Propagation Program for DSPSE Mission Support

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
A New Trajectory Propagation Program for DSPSE Mission Support I I A NEW TRAJECTORY PROPAGATION I PROGRAM FOR DSPSE MISSION SUPPORT I Jay W. Middour* I Naval Center for Space Technology Naval Research Laboratory I Washington, D.C. I Abstract ronment. DSPSE has two secondary science missions in which it will fly in lunar orbit for A satellite trajectory propagation program two months and then depart the Moon for a I called N-Body is being developed to support four month cruise to rendezvous with the near the upcoming Deep Space Program Science Ex­ Earth asteroid 1620 Geographos. In accom­ periment (DSPSE) mission which is also known plishing its secondary missions, DSPSE will I as Clementine. The program will support have made the first complete, multi-spectral the activities of the mission operations center mapping of the lunar surface, and executed the which is run by The Naval Research Labora­ first close encounter with a minor planet (ap­ I tory. The computer program is designed to proximately 100 km). predict a spacecraft orbit through the various Mission operations for DSPSE will be con­ I phases in which the DSPSE vehicle will fly. ducted by the Naval Research Laboratory's These orbital phases include low Earth, trans­ Naval Center for Space Technology at the lunar, lunar, and deep space. The design of DSPSE Mission Operations Center in Alexan­ I N.Body, its functionality, and the mathemati­ dria, Virginia. During the various mission cal methods it employs are presented. phases, the DSPSE space vehicle will fly in low Earth orbit, highly elliptical orbit with apogee I at lunar distances, lunar orbit, and deep space 1 Introduction heliocentric orbit. The DSPSE Mission Op­ erations Center, or DMOC is tasked to coor­ I The Deep Space Science Experiment Pro. dinate the science activities with the business gram (DSPSE), also known as Clementine, of navigation, orbi t determination, command is a joint Naval Research Laboratory, NASA, and telemetry, and satellite housekeeping func­ I and Lawrence Livermore National Laboratory tions. The operations center must therefore project. DSPSE is funded by the Ballistic Mis­ possess a trajectory integration program which sile Defense Office. The primary goal of the can accurately integrate the satellite orbit in I DSPSE mission is to demonstrate the opera­ each of these unique space environments. tion of lightweight sensors in the space envi- It was decided that a program developed by I * Aerospace Engineer, Member AIAA members of the operations team itself could This paper is declared a work of the U.S. Government I and is not subject to copyright protection in the United States. 1 I I be tailored expressly to meet the DSPSE re­ space, the force model must contain the ef­ quirements in areas such as engineering and fects of the Earth and Moon gravitational po­ I science support, contingency planning, maneu­ tential fields, Earth atmospheric drag, solar ver design and verification and tracking sta­ radiation pressure and planetary gravitation. tion scheduling. Furthermore, by using a prod­ Several gravitational potential models for the I uct developed in-house, software modifications Earth and Moon are incorporated into the pro­ can be effected more rapidly and less expen­ gram. Alternatively, a user defined potential sively than if an off-the-shelf product were may be specified. Atmospheric drag requires I used. The trajectory propagation program, a model of the density variations of the Earth called N-Body, is being developed by the au­ atmosphere and a physical model of the satel­ thor to satisfy this requirement. lite. A model of the vehicle shape and its I Strictly speaking, the program does not ad­ specular characteristics are needed to compute dress the classical n-body problem in which the the acceleration due to solar radiation pres­ I motion of n objects under mutual gravitation sure impinging on the spacecraft. A plane­ is solved for. Rather, the program attempts to tary ephemeris is used to obtain the third body solve a restricted problem in which the trajec­ gravitational forces. The planetary ephemeris I tories of n-l objects are known and the motion is also used to predict eclipsing events which af­ of the massless nth object is solved for. In this fect the solar radiation pressure computation. case the n - 1 objects are the Sun, Moon and Finally, the force model allows for impulsive I planets and the nth object is the space vehicle. spacecraft maneuvers. N-Body is written in FORTRAN and is be­ N-Body employs a Cowell method in which I the total accelerations of all external forces act­ ing developed on VAX workstations running ing on the vehicle are directly integrated. Cow­ under the VMS operating system. The com­ ell's method was selected due to its ease of im­ puter code is largely complete and consists of about 10,000 lines. The program is presently I plementation. For instance, Encke's method undergoing verification testing by the DSPSE in which only the perturbations about the two body problem are integrated can be more effi­ mission operations team. It is anticipated that I cient since the integration step size can usually the program will be fully operational in time to be increased over that of the Cowell method support DSPSE flight operations starting with without any associated loss of accuracy. How­ the planned launch in January, 1994. I ever the Encke method requires that the per­ turbed orbit be rectified with a new reference 2 Design and Operation orbit whenever the difference between the per­ I turbed orbit and the reference orbit grows too N-Body is comprised of a program configura­ large. The rectification process logic is depen­ tion procedure, an executive procedure, and I dent on the particular numerical integration an extensive mathematical subroutine library. procedure being used. For instance a multi­ A series of key words and variables is used to step integration method would require restart­ control the execution flow! define the input and I ing. By using Cowell's method, the executive output coordinate frames and times, configure algorithms can be independent of the integra­ the force model, select and configure the in­ tion procedures. The result is a major simpli­ tegrator, set the duration of the propagation I fication in software design and maintenance. and select the destination and frequency of the Since the trajectories must be propagated in output data. The executive procedure trans­ low Earth orbit, trans-lunar, lunar and deep forms the input coordinates and epoch time to I 2 I I I a standard internal fonnat the coordinates of nitions, force model parameters, integrator se­ I which are mean equator and equinox of J2000.0 lection and print options. Each output record and TAl (International Atomic Time) seconds. contains the current time in Julian and calen­ Using the mathematical subroutines! the exec­ dar dates, Cartesian position and velocity, Ke­ I utive procedure carries out the orbit propaga­ plerian orbital elements and Earth referenced tion according to the key word configuration. position of the space vehicle trajectory being I While the propagation is in progress the execu­ integrated. tive procedure monitors its status to detennine An ASCII ephemeris file may be created con­ when output records should be produced. Out­ sisting of a header followed by time, position I put records can be requested at regular time in­ and velocity data records. The header and tervals! after each integration step! at the first data in the ephemeris file conform to the Stan­ and last times in the run or they can be trig­ dard Ephemeris Record Fonnat (SERF) which I gered by orbital events such as apoapsis and will be used by the DSPSE mission operations peri apsis passages. The executive procedure and science teams. The SERF header contains also can be configured to detect the passage of a description of the parameters, constants and I the space vehicle into the umbra and penumbra models used to create the ephemeris. The in­ of a planet, and the occultation of the vehicle put vector coordinate system, origin of coordi­ by a planet as viewed from the Earth. nates, coordinate type, and position, velocity, I The program configuration procedure reads and time units are listed followed by the actual an input file containing key words and vari­ input vector. Generation information is also I ables, as well as the initial condition for the provided which includes the time the run was trajectory that is to be propagated. Each key made, the propagation start and stop times, word and variable is assigned a default value so the interval between ephemeris records, and I that the only item that is required to be in the the number of points in the ephemeris. The input file is the initial condition. The initial force model used for the run is summarized by condition may be specified in tenns of Carte­ listing on I off indicators for Earth harmon­ I sian position and velocity coordinates or clas­ ics, atmospheric drag, solar radiation pressure, sical Keplerian orbital elements. In the case third body perturbations, lunar harmonics and of Keplerian elements, the in-plane position of maneuvering. The output vector coordinates, I the satellite may be specified with either true time, etc. are described in the same manner as anomaly, mean anomaly or time since periap­ the input vector. Finally, The radius and grav­ sis passage. Any of the physical constants used itational parameter of the Earth Moon and Sun I by the program, including the Earth and Moon are listed along with the first four zonals for the gravity models, may be changed by placing the Earth and Moon. I appropriate key words and parameters into the If it has been requested, the executive pro­ input file.
Load more

Recommended publications
  • Analysis of Perturbations and Station-Keeping Requirements in Highly-Inclined Geosynchronous Orbits
    ANALYSIS OF PERTURBATIONS AND STATION-KEEPING REQUIREMENTS IN HIGHLY-INCLINED GEOSYNCHRONOUS ORBITS Elena Fantino(1), Roberto Flores(2), Alessio Di Salvo(3), and Marilena Di Carlo(4) (1)Space Studies Institute of Catalonia (IEEC), Polytechnic University of Catalonia (UPC), E.T.S.E.I.A.T., Colom 11, 08222 Terrassa (Spain), [email protected] (2)International Center for Numerical Methods in Engineering (CIMNE), Polytechnic University of Catalonia (UPC), Building C1, Campus Norte, UPC, Gran Capitan,´ s/n, 08034 Barcelona (Spain) (3)NEXT Ingegneria dei Sistemi S.p.A., Space Innovation System Unit, Via A. Noale 345/b, 00155 Roma (Italy), [email protected] (4)Department of Mechanical and Aerospace Engineering, University of Strathclyde, 75 Montrose Street, Glasgow G1 1XJ (United Kingdom), [email protected] Abstract: There is a demand for communications services at high latitudes that is not well served by conventional geostationary satellites. Alternatives using low-altitude orbits require too large constellations. Other options are the Molniya and Tundra families (critically-inclined, eccentric orbits with the apogee at high latitudes). In this work we have considered derivatives of the Tundra type with different inclinations and eccentricities. By means of a high-precision model of the terrestrial gravity field and the most relevant environmental perturbations, we have studied the evolution of these orbits during a period of two years. The effects of the different perturbations on the constellation ground track (which is more important for coverage than the orbital elements themselves) have been identified. We show that, in order to maintain the ground track unchanged, the most important parameters are the orbital period and the argument of the perigee.
    [Show full text]
  • Astrodynamics
    Politecnico di Torino SEEDS SpacE Exploration and Development Systems Astrodynamics II Edition 2006 - 07 - Ver. 2.0.1 Author: Guido Colasurdo Dipartimento di Energetica Teacher: Giulio Avanzini Dipartimento di Ingegneria Aeronautica e Spaziale e-mail: [email protected] Contents 1 Two–Body Orbital Mechanics 1 1.1 BirthofAstrodynamics: Kepler’sLaws. ......... 1 1.2 Newton’sLawsofMotion ............................ ... 2 1.3 Newton’s Law of Universal Gravitation . ......... 3 1.4 The n–BodyProblem ................................. 4 1.5 Equation of Motion in the Two-Body Problem . ....... 5 1.6 PotentialEnergy ................................. ... 6 1.7 ConstantsoftheMotion . .. .. .. .. .. .. .. .. .... 7 1.8 TrajectoryEquation .............................. .... 8 1.9 ConicSections ................................... 8 1.10 Relating Energy and Semi-major Axis . ........ 9 2 Two-Dimensional Analysis of Motion 11 2.1 ReferenceFrames................................. 11 2.2 Velocity and acceleration components . ......... 12 2.3 First-Order Scalar Equations of Motion . ......... 12 2.4 PerifocalReferenceFrame . ...... 13 2.5 FlightPathAngle ................................. 14 2.6 EllipticalOrbits................................ ..... 15 2.6.1 Geometry of an Elliptical Orbit . ..... 15 2.6.2 Period of an Elliptical Orbit . ..... 16 2.7 Time–of–Flight on the Elliptical Orbit . .......... 16 2.8 Extensiontohyperbolaandparabola. ........ 18 2.9 Circular and Escape Velocity, Hyperbolic Excess Speed . .............. 18 2.10 CosmicVelocities
    [Show full text]
  • A Hot Subdwarf-White Dwarf Super-Chandrasekhar Candidate
    A hot subdwarf–white dwarf super-Chandrasekhar candidate supernova Ia progenitor Ingrid Pelisoli1,2*, P. Neunteufel3, S. Geier1, T. Kupfer4,5, U. Heber6, A. Irrgang6, D. Schneider6, A. Bastian1, J. van Roestel7, V. Schaffenroth1, and B. N. Barlow8 1Institut fur¨ Physik und Astronomie, Universitat¨ Potsdam, Haus 28, Karl-Liebknecht-Str. 24/25, D-14476 Potsdam-Golm, Germany 2Department of Physics, University of Warwick, Coventry, CV4 7AL, UK 3Max Planck Institut fur¨ Astrophysik, Karl-Schwarzschild-Straße 1, 85748 Garching bei Munchen¨ 4Kavli Institute for Theoretical Physics, University of California, Santa Barbara, CA 93106, USA 5Texas Tech University, Department of Physics & Astronomy, Box 41051, 79409, Lubbock, TX, USA 6Dr. Karl Remeis-Observatory & ECAP, Astronomical Institute, Friedrich-Alexander University Erlangen-Nuremberg (FAU), Sternwartstr. 7, 96049 Bamberg, Germany 7Division of Physics, Mathematics and Astronomy, California Institute of Technology, Pasadena, CA 91125, USA 8Department of Physics and Astronomy, High Point University, High Point, NC 27268, USA *[email protected] ABSTRACT Supernova Ia are bright explosive events that can be used to estimate cosmological distances, allowing us to study the expansion of the Universe. They are understood to result from a thermonuclear detonation in a white dwarf that formed from the exhausted core of a star more massive than the Sun. However, the possible progenitor channels leading to an explosion are a long-standing debate, limiting the precision and accuracy of supernova Ia as distance indicators. Here we present HD 265435, a binary system with an orbital period of less than a hundred minutes, consisting of a white dwarf and a hot subdwarf — a stripped core-helium burning star.
    [Show full text]
  • Electric Propulsion System Scaling for Asteroid Capture-And-Return Missions
    Electric propulsion system scaling for asteroid capture-and-return missions Justin M. Little⇤ and Edgar Y. Choueiri† Electric Propulsion and Plasma Dynamics Laboratory, Princeton University, Princeton, NJ, 08544 The requirements for an electric propulsion system needed to maximize the return mass of asteroid capture-and-return (ACR) missions are investigated in detail. An analytical model is presented for the mission time and mass balance of an ACR mission based on the propellant requirements of each mission phase. Edelbaum’s approximation is used for the Earth-escape phase. The asteroid rendezvous and return phases of the mission are modeled as a low-thrust optimal control problem with a lunar assist. The numerical solution to this problem is used to derive scaling laws for the propellant requirements based on the maneuver time, asteroid orbit, and propulsion system parameters. Constraining the rendezvous and return phases by the synodic period of the target asteroid, a semi- empirical equation is obtained for the optimum specific impulse and power supply. It was found analytically that the optimum power supply is one such that the mass of the propulsion system and power supply are approximately equal to the total mass of propellant used during the entire mission. Finally, it is shown that ACR missions, in general, are optimized using propulsion systems capable of processing 100 kW – 1 MW of power with specific impulses in the range 5,000 – 10,000 s, and have the potential to return asteroids on the order of 103 104 tons. − Nomenclature
    [Show full text]
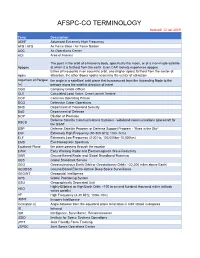
  • AFSPC-CO TERMINOLOGY Revised: 12 Jan 2019
    AFSPC-CO TERMINOLOGY Revised: 12 Jan 2019 Term Description AEHF Advanced Extremely High Frequency AFB / AFS Air Force Base / Air Force Station AOC Air Operations Center AOI Area of Interest The point in the orbit of a heavenly body, specifically the moon, or of a man-made satellite Apogee at which it is farthest from the earth. Even CAP rockets experience apogee. Either of two points in an eccentric orbit, one (higher apsis) farthest from the center of Apsis attraction, the other (lower apsis) nearest to the center of attraction Argument of Perigee the angle in a satellites' orbit plane that is measured from the Ascending Node to the (ω) perigee along the satellite direction of travel CGO Company Grade Officer CLV Calculated Load Value, Crew Launch Vehicle COP Common Operating Picture DCO Defensive Cyber Operations DHS Department of Homeland Security DoD Department of Defense DOP Dilution of Precision Defense Satellite Communications Systems - wideband communications spacecraft for DSCS the USAF DSP Defense Satellite Program or Defense Support Program - "Eyes in the Sky" EHF Extremely High Frequency (30-300 GHz; 1mm-1cm) ELF Extremely Low Frequency (3-30 Hz; 100,000km-10,000km) EMS Electromagnetic Spectrum Equitorial Plane the plane passing through the equator EWR Early Warning Radar and Electromagnetic Wave Resistivity GBR Ground-Based Radar and Global Broadband Roaming GBS Global Broadcast Service GEO Geosynchronous Earth Orbit or Geostationary Orbit ( ~22,300 miles above Earth) GEODSS Ground-Based Electro-Optical Deep Space Surveillance
    [Show full text]
  • Use of MESSENGER Radioscience Data to Improve Planetary Ephemeris and to Test General Relativity
    A&A 561, A115 (2014) Astronomy DOI: 10.1051/0004-6361/201322124 & © ESO 2014 Astrophysics Use of MESSENGER radioscience data to improve planetary ephemeris and to test general relativity A. K. Verma1;2, A. Fienga3;4, J. Laskar4, H. Manche4, and M. Gastineau4 1 Observatoire de Besançon, UTINAM-CNRS UMR6213, 41bis avenue de l’Observatoire, 25000 Besançon, France e-mail: [email protected] 2 Centre National d’Études Spatiales, 18 avenue Édouard Belin, 31400 Toulouse, France 3 Observatoire de la Côte d’Azur, GéoAzur-CNRS UMR7329, 250 avenue Albert Einstein, 06560 Valbonne, France 4 Astronomie et Systèmes Dynamiques, IMCCE-CNRS UMR8028, 77 Av. Denfert-Rochereau, 75014 Paris, France Received 24 June 2013 / Accepted 7 November 2013 ABSTRACT The current knowledge of Mercury’s orbit has mainly been gained by direct radar ranging obtained from the 60s to 1998 and by five Mercury flybys made with Mariner 10 in the 70s, and with MESSENGER made in 2008 and 2009. On March 18, 2011, MESSENGER became the first spacecraft to orbit Mercury. The radioscience observations acquired during the orbital phase of MESSENGER drastically improved our knowledge of the orbit of Mercury. An accurate MESSENGER orbit is obtained by fitting one-and-half years of tracking data using GINS orbit determination software. The systematic error in the Earth-Mercury geometric positions, also called range bias, obtained from GINS are then used to fit the INPOP dynamical modeling of the planet motions. An improved ephemeris of the planets is then obtained, INPOP13a, and used to perform general relativity tests of the parametrized post-Newtonian (PPN) formalism.
    [Show full text]
  • Chapter 2: Earth in Space
    Chapter 2: Earth in Space 1. Old Ideas, New Ideas 2. Origin of the Universe 3. Stars and Planets 4. Our Solar System 5. Earth, the Sun, and the Seasons 6. The Unique Composition of Earth Copyright © The McGraw-Hill Companies, Inc. Permission required for reproduction or display. Earth in Space Concept Survey Explain how we are influenced by Earth’s position in space on a daily basis. The Good Earth, Chapter 2: Earth in Space Old Ideas, New Ideas • Why is Earth the only planet known to support life? • How have our views of Earth’s position in space changed over time? • Why is it warmer in summer and colder in winter? (or, How does Earth’s position relative to the sun control the “Earthrise” taken by astronauts aboard Apollo 8, December 1968 climate?) The Good Earth, Chapter 2: Earth in Space Old Ideas, New Ideas From a Geocentric to Heliocentric System sun • Geocentric orbit hypothesis - Ancient civilizations interpreted rising of sun in east and setting in west to indicate the sun (and other planets) revolved around Earth Earth pictured at the center of a – Remained dominant geocentric planetary system idea for more than 2,000 years The Good Earth, Chapter 2: Earth in Space Old Ideas, New Ideas From a Geocentric to Heliocentric System • Heliocentric orbit hypothesis –16th century idea suggested by Copernicus • Confirmed by Galileo’s early 17th century observations of the phases of Venus – Changes in the size and shape of Venus as observed from Earth The Good Earth, Chapter 2: Earth in Space Old Ideas, New Ideas From a Geocentric to Heliocentric System • Galileo used early telescopes to observe changes in the size and shape of Venus as it revolved around the sun The Good Earth, Chapter 2: Earth in Space Earth in Space Conceptest The moon has what type of orbit? A.
    [Show full text]
  • The Minor Planet Bulletin
    THE MINOR PLANET BULLETIN OF THE MINOR PLANETS SECTION OF THE BULLETIN ASSOCIATION OF LUNAR AND PLANETARY OBSERVERS VOLUME 36, NUMBER 3, A.D. 2009 JULY-SEPTEMBER 77. PHOTOMETRIC MEASUREMENTS OF 343 OSTARA Our data can be obtained from http://www.uwec.edu/physics/ AND OTHER ASTEROIDS AT HOBBS OBSERVATORY asteroid/. Lyle Ford, George Stecher, Kayla Lorenzen, and Cole Cook Acknowledgements Department of Physics and Astronomy University of Wisconsin-Eau Claire We thank the Theodore Dunham Fund for Astrophysics, the Eau Claire, WI 54702-4004 National Science Foundation (award number 0519006), the [email protected] University of Wisconsin-Eau Claire Office of Research and Sponsored Programs, and the University of Wisconsin-Eau Claire (Received: 2009 Feb 11) Blugold Fellow and McNair programs for financial support. References We observed 343 Ostara on 2008 October 4 and obtained R and V standard magnitudes. The period was Binzel, R.P. (1987). “A Photoelectric Survey of 130 Asteroids”, found to be significantly greater than the previously Icarus 72, 135-208. reported value of 6.42 hours. Measurements of 2660 Wasserman and (17010) 1999 CQ72 made on 2008 Stecher, G.J., Ford, L.A., and Elbert, J.D. (1999). “Equipping a March 25 are also reported. 0.6 Meter Alt-Azimuth Telescope for Photometry”, IAPPP Comm, 76, 68-74. We made R band and V band photometric measurements of 343 Warner, B.D. (2006). A Practical Guide to Lightcurve Photometry Ostara on 2008 October 4 using the 0.6 m “Air Force” Telescope and Analysis. Springer, New York, NY. located at Hobbs Observatory (MPC code 750) near Fall Creek, Wisconsin.
    [Show full text]
  • 1620 Geographos and 433 Eros: Shaped by Planetary Tides?
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by CERN Document Server 1620 Geographos and 433 Eros: Shaped by Planetary Tides? W. F. Bottke, Jr. Center for Radiophysics and Space Research, Cornell University, Ithaca, NY 14853-6801 D. C. Richardson Department of Astronomy, University of Washington, Box 351580, Seattle, WA 98195 P. Michel Osservatorio Astronomico di Torino, Strada Osservatorio 20, 10025 Pino Torinese (TO), Italy and S. G. Love Jet Propulsion Laboratory, California Institute of Technology, M/S 306-438, 4800 Oak Grove Drive, Pasadena, CA 91109-8099 Received 23 September 1998; accepted 10 December 1998 –2– ABSTRACT Until recently, most asteroids were thought to be solid bodies whose shapes were determined largely by collisions with other asteroids (Davis et al., 1989). It now seems that many asteroids are little more than rubble piles, held together by self-gravity (Burns 1998); this means that their shapes may be strongly distorted by tides during close encounters with planets. Here we report on numerical simulations of encounters between a ellipsoid-shaped rubble-pile asteroid and the Earth. After an encounter, many of the simulated asteroids develop the same rotation rate and distinctive shape (i.e., highly elongated with a single convex side, tapered ends, and small protuberances swept back against the rotation direction) as 1620 Geographos. Since our numerical studies show that these events occur with some frequency, we suggest that Geographos may be a tidally distorted object. In addition, our work shows that 433 Eros, which will be visited by the NEAR spacecraft in 1999, is much like Geographos, which suggests that it too may have been molded by tides in the past.
    [Show full text]
  • A Highly Elliptical Orbit Space System for Hydrometeorological Monitoring of the Arctic Region by V
    A highly elliptical orbit space system for hydrometeorological monitoring of the Arctic region by V. V. Asmus1, V. N. Dyadyuchenko2, Y. I. Nosenko3, G. M. Polishchuk4 and V. A. Selin3 The lack of reliable, frequently high latitudes. It has therefore been • Monitoring of climate change updated information on the Earth’s suggested that demonstration of polar ice caps is a signifi cant problem a hydrometeorological system of • Data collection and relay for weather forecasting, affecting satellites on highly elliptical orbit from land-, sea- and air-based forecast skill for the entire planet. The (HEO), called the “Arctica” system, observing platforms poor numerical weather prediction should be created to provide the (NWP) skill for the Arctic region necessary complex information for the • Exchange and dissemination of and the Earth’s northern territories diffi cult tasks involved in developing processed hydrometeorological is caused primarily by errors in the whole Arctic region. and heliogeophysical data. determining initial conditions, which depend on the quality of initial Signifi cantly, the hydrometeorological Further progress in global and data. Until now, initial data have observations carried out in the regional numerical weather prediction been received from meteorological Arctic within the framework of the depends to a large extent on: geostationary satellites, which are International Polar Year 2007-2008 not very effective in scanning high are not provided with remote-sensing • Quasi-continuous reception latitudes and polar-orbiting
    [Show full text]
  • GPS Applications in Space
    Space Situational Awareness 2015: GPS Applications in Space James J. Miller, Deputy Director Policy & Strategic Communications Division May 13, 2015 GPS Extends the Reach of NASA Networks to Enable New Space Ops, Science, and Exploration Apps GPS Relative Navigation is used for Rendezvous to ISS GPS PNT Services Enable: • Attitude Determination: Use of GPS enables some missions to meet their attitude determination requirements, such as ISS • Real-time On-Board Navigation: Enables new methods of spaceflight ops such as rendezvous & docking, station- keeping, precision formation flying, and GEO satellite servicing • Earth Sciences: GPS used as a remote sensing tool supports atmospheric and ionospheric sciences, geodesy, and geodynamics -- from monitoring sea levels and ice melt to measuring the gravity field ESA ATV 1st mission JAXA’s HTV 1st mission Commercial Cargo Resupply to ISS in 2008 to ISS in 2009 (Space-X & Cygnus), 2012+ 2 Growing GPS Uses in Space: Space Operations & Science • NASA strategic navigation requirements for science and 20-Year Worldwide Space Mission space ops continue to grow, especially as higher Projections by Orbit Type* precisions are needed for more complex operations in all space domains 1% 5% Low Earth Orbit • Nearly 60%* of projected worldwide space missions 27% Medium Earth Orbit over the next 20 years will operate in LEO 59% GeoSynchronous Orbit – That is, inside the Terrestrial Service Volume (TSV) 8% Highly Elliptical Orbit Cislunar / Interplanetary • An additional 35%* of these space missions that will operate at higher altitudes will remain at or below GEO – That is, inside the GPS/GNSS Space Service Volume (SSV) Highly Elliptical Orbits**: • In summary, approximately 95% of projected Example: NASA MMS 4- worldwide space missions over the next 20 years will satellite constellation.
    [Show full text]
  • Open Rosen Thesis.Pdf
    THE PENNSYLVANIA STATE UNIVERSITY SCHREYER HONORS COLLEGE DEPARTMENT OF AEROSPACE ENGINEERING END OF LIFE DISPOSAL OF SATELLITES IN HIGHLY ELLIPTICAL ORBITS MITCHELL ROSEN SPRING 2019 A thesis submitted in partial fulfillment of the requirements for a baccalaureate degree in Aerospace Engineering with honors in Aerospace Engineering Reviewed and approved* by the following: Dr. David Spencer Professor of Aerospace Engineering Thesis Supervisor Dr. Mark Maughmer Professor of Aerospace Engineering Honors Adviser * Signatures are on file in the Schreyer Honors College. i ABSTRACT Highly elliptical orbits allow for coverage of large parts of the Earth through a single satellite, simplifying communications in the globe’s northern reaches. These orbits are able to avoid drastic changes to the argument of periapse by using a critical inclination (63.4°) that cancels out the first level of the geopotential forces. However, this allows the next level of geopotential forces to take over, quickly de-orbiting satellites. Thus, a balance between the rate of change of the argument of periapse and the lifetime of the orbit is necessitated. This thesis sets out to find that balance. It is determined that an orbit with an inclination of 62.5° strikes that balance best. While this orbit is optimal off of the critical inclination, it is still near enough that to allow for potential use of inclination changes as a deorbiting method. Satellites are deorbited when the propellant remaining is enough to perform such a maneuver, and nothing more; therefore, the less change in velocity necessary for to deorbit, the better. Following the determination of an ideal highly elliptical orbit, the different methods of inclination change is tested against the usual method for deorbiting a satellite, an apoapse burn to lower the periapse, to find the most propellant- efficient method.
    [Show full text]