The Three-Color Triangle Problem
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Light and Color
Chapter 9 LIGHT AND COLOR What Is Color? Color is a human phenomenon. To the physicist, the only difference be- tween light with a wavelength of 400 nanometers and that of 700 nm is Different wavelengths wavelength and amount of energy. However a normal human eye will see cause the eye to see another very significant difference: The shorter wavelength light will different colors. cause the eye to see blue-violet and the longer, deep red. Thus color is the response of the normal eye to certain wavelengths of light. It is nec- essary to include the qualifier “normal” because some eyes have abnor- malities which makes it impossible for them to distinguish between certain colors, red and green, for example. Note that “color” is something that happens in the human seeing ap- Only light itself paratus—when the eye perceives certain wavelengths of light. There is causes sensations of no mention of paint, pigment, ink, colored cloth or anything except light color. itself. Clear understanding of this point is vital to the forthcoming discus- sion. Colorants by themselves cannot produce sensations of color. If the proper light waves are not present, colorants are helpless to produce a sensation of color. Thus color resides in the eye, actually in the retina- optic-nerve-brain combination which teams up to provide our color sen- Color vision is sations. How this system works has been a matter of study for many years complex and not and recent investigations, many of them based on the availability of new completely brain scanning machines, have made important discoveries. -

Goethe's Theory of Colors Between the Ancient Philosophy, Middle Ages
CULTURE, MEDIA & FILM | RESEARCH ARTICLE Goethe’s theory of colors between the ancient philosophy, middle ages occultism and modern science Victor Barsan and Andrei Merticariu Cogent Arts & Humanities (2016), 3: 1145569 Page 1 of 29 Barsan & Merticariu, Cogent Arts & Humanities (2016), 3: 1145569 http://dx.doi.org/10.1080/23311983.2016.1145569 CULTURE, MEDIA & FILM | RESEARCH ARTICLE Goethe’s theory of colors between the ancient philosophy, middle ages occultism and modern science 1 2 Received: 18 February 2015 Victor Barsan * and Andrei Merticariu Accepted: 20 January 2016 Published: 18 February 2016 Abstract: Goethe’s rejection of Newton’s theory of colors is an interesting example *Corresponding author: Victor Barsan, of the vulnerability of the human mind—however brilliant it might be—to fanati- Department of Theoretical Physics, cism. After an analysis of Goethe’s persistent fascination with magic and occultism, Horia Hulubei Institute of Physics and Nuclear Engineering, Aleea Reactorului of his education, existential experiences, influences, and idiosyncrasies, the authors nr. 30, Magurele, Bucharest, Romania E-mail: [email protected] propose an original interpretation of his anti-Newtonian position. The relevance of Goethe’s Farbenlehre to physics and physiology, from the perspective of modern sci- Reviewing editor: Peter Stanley Fosl, Transylvania ence, is discussed in detail. University, USA Subjects: Aristotle; Biophysics; Experimental Physics; Fine Art; Medical Physics; Ophthal- Additional information is available at the end of the article mology; Philosophy of Art; Philosophy of Science; Presocratics Keywords: ancient philosophy; Greek–Roman classicism; middle ages science; Newtonian science; occultism; pantheism; optics; theory of colors; primordial phenomenon (urphaeno men) 1. Introduction Light is one of the most interesting components of the physical universe. -

Fuzzy Set Theoretical Approach to the Tone Triangular System
JOURNAL OF COMPUTERS, VOL. 6, NO. 11, NOVEMBER 2011 2345 Fuzzy Set Theoretical Approach to the Tone Triangular System Naotoshi Sugano Tamagawa University, Tokyo, Japan [email protected] Abstract—The present study considers a fuzzy color system gravity of the attribute information of vague colors. This in which three input fuzzy sets are constructed on the tone fuzzy set theoretical approach is useful for vague color triangle. This system can process a fuzzy input to a tone information processing, color identification, and similar triangular system and output to a color on the RGB applications. triangular system. Three input fuzzy sets (not black, white, and light) are applied to the tone triangle relationship. By treating three attributes of chromaticness, whiteness, and II. METHODS blackness on the tone triangle, a target color can be easily A. Color Triangle and Additive Color Mixture obtained as the center of gravity of the output fuzzy set. In Additive color mixing occurs when two or three beams the present paper, the differences between fuzzy inputs and inference outputs are described, and the relationship of differently colored light combine. It has been found between inference outputs for crisp inputs and for fuzzy that mixing just three additive primary colors, red, green, inputs on the RGB triangular system are shown by the and blue, can produce the majority of colors. In general, a input-output characteristics between chromaticness, color vector can be described by certain quantities as a whiteness, and blackness as the inputs and redness (as one scalar and a direction. These quantities are referred to as of the outputs). -

A Correlated Color Temperature for Illuminants
. (R P 365) A CORRELATED COLOR TEMPERATURE FOR ILLUMINANTS By Raymond Davis ABSTRACT As has long been known, most of the artificial and natural illuminants do not match exactly any one of the Planckian colors. Therefore, strictly speaking, they can not be assigned a color temperature. A color of this type may, however, be correlated with a representative Planckian color. The method of determining correlated color temperature described in this paper consists in comparing the relative luminosities of each of the three primary red, green, and blue components of the source with similar values for the Planckian series. With such a comparison three component temperatures are obtained; that is, the red component of the source corresponds with that of the Planckian radiator at one temperature, its green component with that of the Planckian radiator at a second temperature, and its blue component with that of the Planckian radiator at a third temperature. The average of these three component temperatures is designated as the correlated color temperature of the source. The mean devia- tion of the component temperatures from the average temperature is used as a basis for specifying the color (chromaticity) departure of the source from that of the Planckian radiator at the correlated color temperature. The conjunctive wave length indicates the kind of color departure. CONTENTS Page I. Introduction 659 II. The proposed method 662 III. Procedure 665 1. The Planckian radiator evaluated in terms of relative lumi- nosity of the primary components 665 2. Computation of the correlated color temperature 670 3. Calculation of color departure in terms of sensation steps 672 4. -

Raphics & Visualization
Graphics & Visualization Chapter 11 COLOR IN GRAPHICS & VISUALIZATION Graphics & Visualization: Principles & Algorithms Chapter 11 Introduction • The study of color, and the way humans perceive it, a branch of: Physics Physiology Psychology Computer Graphics Visualization • The result of graphics or visualization algorithms is a color or grayscale image to be viewed on an output device (monitor, printer) Graphics programmer should be aware of the fundamental principles behind color and its digital representation Graphics & Visualization: Principles & Algorithms Chapter 11 2 Grayscale • Intensity: achromatic light; color characteristics removed • Intensity can be represented by a real number between 0 (black) and 1 (white) Values between these two extremes are called grayscales • Assume use of d bits to represent the intensity of each pixel n=2d different intensity values per pixel • Question: which intensity values shall we represent ? • Answer: Linear scale of intensities between the minimum & maximum value, is not a good idea: Human eye perceives intensity ratios rather than absolute intensity values. Light bulb example: 20-40-60W Therefore, we opt for a logarithmic distribution of intensity values Graphics & Visualization: Principles & Algorithms Chapter 11 3 Grayscale (2) • Let Φ0 be the minimum intensity value For typical monitors: Φ0 = (1/300) * maximum value 1 (white) Such monitors have a dynamic range of 300:1 • Let λ be the ratio between successive intensity values • Then we take: Φ1 = λ* Φ0 2 Φ1 = λ* Φ1=λ *Φ0 … -

Computer Vision? Color Histograms
Lecture 11 Color © UW CSE vision faculty Starting Point: What is light? Electromagnetic radiation (EMR) moving along rays in space •R(λ) is EMR, measured in units of power (watts) – λ is wavelength Perceiving light • How do we convert radiation into “color”? • What part of the spectrum do we see? Newton’s prism experiment Newton’s own drawing of his experiment showing decomposition of white light The light spectrum We “see” electromagnetic radiation in a range of wavelengths Light spectrum The appearance of light depends on its power spectrum • How much power (or energy) at each wavelength daylight tungsten bulb Our visual system converts a light spectrum into “color” • This is a rather complex transformation Recall: Image Formation Basics i(x,y) f(x,y) r(x,y) (from Gonzalez & Woods, 2008) Image Formation: Basics Image f(x,y) is characterized by 2 components 1. Illumination i(x,y) = Amount of source illumination incident on scene 2. Reflectance r(x,y) = Amount of illumination reflected by objects in the scene f(,)(,)(,) x y i= x y r x y where 0 (< ,i ) x < y ∞andr 0 < x y ( , < ) 1 r(x,y) depends on object properties r = 0 means total absorption and 1 means total reflectance The Human Eye and Retina Color perception • Light hits the retina, which contains photosensitive cells – rods and cones • Rods responsible for intensity, cones responsible for color Density of rods and cones Rods and cones are non-uniformly distributed on the retina • Fovea - Small central region (1 or 2°) containing the highest density of cones (and no rods) • Less visual acuity in the periphery—many rods wired to the same neuron Demonstration of Blind Spot With left eye shut, look at the cross on the left. -

Colorwatch: Color Perceptual Spatial Tactile Interface for People with Visual Impairments
electronics Article ColorWatch: Color Perceptual Spatial Tactile Interface for People with Visual Impairments Muhammad Shahid Jabbar 1 , Chung-Heon Lee 1 and Jun Dong Cho 1,2,* 1 Department of Electrical and Computer Engineering, Sungkyunkwan University, Suwon 16419, Gyeonggi-do, Korea; [email protected] (M.S.J.); [email protected] (C.-H.L.) 2 Department of Human ICT Convergence, Sungkyunkwan University, Suwon 16419, Gyeonggi-do, Korea * Correspondence: [email protected] Abstract: Tactile perception enables people with visual impairments (PVI) to engage with artworks and real-life objects at a deeper abstraction level. The development of tactile and multi-sensory assistive technologies has expanded their opportunities to appreciate visual arts. We have developed a tactile interface based on the proposed concept design under considerations of PVI tactile actuation, color perception, and learnability. The proposed interface automatically translates reference colors into spatial tactile patterns. A range of achromatic colors and six prominent basic colors with three levels of chroma and values are considered for the cross-modular association. In addition, an analog tactile color watch design has been proposed. This scheme enables PVI to explore artwork or real-life object color by identifying the reference colors through a color sensor and translating them to the tactile interface. The color identification tests using this scheme on the developed prototype exhibit good recognition accuracy. The workload assessment and usability evaluation for PVI demonstrate promising results. This suggest that the proposed scheme is appropriate for tactile color exploration. Citation: Jabbar, M.S.; Lee, C.-H.; Keywords: color identification; tactile perception; cross modular association; universal design; Cho, J.D. -

Evaluating Color Gamut of Smartphone Display
Evaluating Color Gamut of Smartphone Display Introduction gamut, but the most common reference spaces used for display products are CIE Yxy (1931) and CIE Lu’v’ With increased image and video content available over (1976) chromaticity chart. the internet, there is now a growing emphasis on color fidelity and accuracy of display used in smartphone. One reason for this growing emphasis is the emergence of online merchandising. Consumers want to be sure that the colors they see on their smartphone display are actually what they will get eventually. Another reason is CIE Yxy (1931) chromaticity chart that we are now accustomed to seeing displays which are able to reproduce colors we see in the real world. Anything less, the smartphone display would be deemed as mediocre. The good news is color fidelity and accuracy of display have improved throughout the years due to better display technology, advanced signal processing and color management solution. To ensure displays are able to portray specific colors accurately, evaluating parameter like color gamut is CIE Lu’v’ (1976) chromaticity chart necessary. Apart from color gamut, parameters like white point and gamma are also of equal importance TThere are various color gamut standards drafted for in evaluating the visual characteristic of display. expressing color display range according to different industry and different application. For smartphone What is Color Gamut? and PC displays, the standard gamut is sRGB/ Rec.709. However, with the growing adoption of wide color Color gamut is defined as the range of colors that a gamut solutions in the high-end display market, wide display can reproduce. -

An Integrative Framework for the Appraisal of Coloration in Nature Author(S): Darrell J
The University of Chicago An Integrative Framework for the Appraisal of Coloration in Nature Author(s): Darrell J. Kemp, Marie E. Herberstein, Leo J. Fleishman, John A. Endler, Andrew T. D. Bennett, Adrian G. Dyer, Nathan S. Hart, Justin Marshall, Martin J. Whiting Source: The American Naturalist, Vol. 185, No. 6 (June 2015), pp. 705-724 Published by: The University of Chicago Press for The American Society of Naturalists Stable URL: http://www.jstor.org/stable/10.1086/681021 . Accessed: 07/10/2015 01:10 Your use of the JSTOR archive indicates your acceptance of the Terms & Conditions of Use, available at . http://www.jstor.org/page/info/about/policies/terms.jsp . JSTOR is a not-for-profit service that helps scholars, researchers, and students discover, use, and build upon a wide range of content in a trusted digital archive. We use information technology and tools to increase productivity and facilitate new forms of scholarship. For more information about JSTOR, please contact [email protected]. The University of Chicago Press, The American Society of Naturalists, The University of Chicago are collaborating with JSTOR to digitize, preserve and extend access to The American Naturalist. http://www.jstor.org This content downloaded from 23.235.32.0 on Wed, 7 Oct 2015 01:10:39 AM All use subject to JSTOR Terms and Conditions vol. 185, no. 6 the american naturalist june 2015 Synthesis An Integrative Framework for the Appraisal of Coloration in Nature Darrell J. Kemp,1,* Marie E. Herberstein,1 Leo J. Fleishman,2 John A. Endler,3,4 Andrew T. -
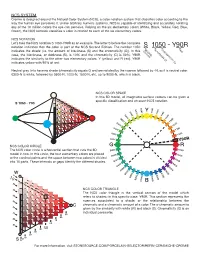
Cromie Is Designed Around the Natural Color System (NCS), a Color Notation System That Classifies Color According to the Way the Human Eye Perceives It
NCS SYSTEM Cromie is designed around the Natural Color System (NCS), a color notation system that classifies color according to the way the human eye perceives it. Unlike arbitrary numeric systems, NCS is capable of identifying and accurately notating any of the 10 million colors the eye can perceive. Relying on the six elementary colors (White, Black, Yellow, Red, Blue, Green), the NCS notation classifies a color in relation to each of the six elementary colors. NCS NOTATION Let’s take the NCS notation S 1050-Y90R as an example. The letter S before the complete notation indicates that the color is part of the NCS Second Edition. The number 1050 indicates the shade (i.e. the amount of blackness (S) and the chromaticity (C)). In this case, the blackness, or darkness (S), is 10% and the chromaticity (C) is 50%. Y90R indicates the similarity to the other two elementary colors, Y (yellow) and R (red). Y90R indicates yellow with 90% of red. Neutral gray tints have no shade (chromaticity equals 0) and are notated by the nuance followed by -N, as it is neutral color. 0300-N is white, followed by 0500-N, 1000-N, 1500 N, etc. up to 9000-N, which is black. NCS COLOR SPACE In this 3D model, all imaginable surface colours can be given a specific classification and an exact NCS notation. S 1050 - Y90 NCS COLOR CIRCLE The NCS color circle is a horizontal section that cuts the 3D model in two. In this circle, the four elementary colors are placed at the cardinal points and the space between two colors is divided into 10 parts. -

Realizing Rec. 2020 Color Gamut with Quantum Dot Displays
Realizing Rec. 2020 color gamut with quantum dot displays Ruidong Zhu,1 Zhenyue Luo,1 Haiwei Chen,1 Yajie Dong,1,2 and Shin-Tson Wu1,* 1CREOL, The College of Optics and Photonics, University of Central Florida, Orlando, Florida 32816, USA 2NanoScience Technology Center, University of Central Florida, Orlando, Florida 32826, USA *[email protected] Abstract: We analyze how to realize Rec. 2020 wide color gamut with quantum dots. For photoluminescence, our simulation indicates that we are able to achieve over 97% of the Rec. 2020 standard with quantum dots by optimizing the emission spectra and redesigning the color filters. For electroluminescence, by optimizing the emission spectra of quantum dots is adequate to render over 97% of the Rec. 2020 standard. We also analyze the efficiency and angular performance of these devices, and then compare results with LCDs using green and red phosphors-based LED backlight. Our results indicate that quantum dot display is an outstanding candidate for achieving wide color gamut and high optical efficiency. ©2015 Optical Society of America OCIS codes: (250.5590) Optoelectronics: Quantum-well, -wire and -dot devices; (330.1715) Color, rendering and metamerism; (230.3670) Light-emitting diodes; (230.3720) Liquid-crystal devices. References and links 1. Adobe Systems Inc., “Adobe RGB (1998) color image encoding,” 2005. 2. SMPTE RP 431–2, “D-cinema quality — reference projector and environment,” 2011. 3. ITU-R Recommendation BT.709–5, “Parameter values for the HDTV standards for production and international programme exchange,” 2002. 4. ITU-R Recommendation BT.2020, “Parameter values for ultra-high definition television systems for production and international programme exchange,” 2012. -

Primary and Secondary Analogous Colours Complementary Colours
Colour Theory: Primary and Secondary The primary colors are yellow, red, and blue. Secondary colors are created when equal amounts of any two primary colors are mixed together. The secondary colors orange, violet, and green are located on the sides of the color triangle. Analogous Colours The term analogous means ““like”” or ““similar.”” Analogous color can be used to create subtle differences in an image or design. These subtle differences create a peaceful and more harmonious feeling from an image. Complementary Colours Find a primary color on the color triangle. Draw a line directly opposite the color and you have discovered the complementary color. As opposites on the color triangle, the colors react off one another visually when placed alongside each another. This effect has been described as creating energy, or a visual vibration, that can be used if those results are desired. Split Complementary Colour Schemes A Split complement color scheme is created by combining a color on one side of the color wheel with two colors on either side of its direct complement. An example would be blue with yellow-orange and red-orange. These colors contrast less than the direct complement. This adds interest and variety. Pros: This scheme has more variety than a simple complementary color scheme. Cons: It is less vibrant and eye-catching. It is difficult to harmonize the colors. Tints and Shades When white is added to a color, the color is diluted and produces a tint (also referred to as pastels). A shade is created when a color is mixed with black.