Structural Analysis of Components Obtained by the Injection Molding Process
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Download the PLM Industry Summary (PDF)
PLM Industry Summary Christine Bennett, Editor Vol. 13 No.17 Friday 29 April 2011 Contents Acquisitions _______________________________________________________________________ 2 Dassault Systèmes Acquires Enginuity PLM to Accelerate Innovation for Formulated Products __________2 ESI Group Acquires Comet Technology’s IP, Including “COMET Acoustics” Software for Low Frequency Noise and Vibration Modeling _____________________________________________________________4 Lawson Software Enters into Definitive Agreement to be Acquired by an Affiliate of Golden Gate Capital and Infor ______________________________________________________________________________4 CIMdata News _____________________________________________________________________ 6 CIMdata in the News: “CIMdata Evaluates PLM-Market in 2010 and Gives Optimistic Forecasts” _______6 YouTube: Oracle Agile PLM Team Interviews CIMdata Analyst _________________________________6 Company News _____________________________________________________________________ 6 CGTech and VMH International Announce Joint Partnership _____________________________________6 Delcam Wins Third Queen’s Award for International Sales Success _______________________________7 500 Technical Paper and Presentations on Multiphysics Simulation are Available from COMSOL________8 POLYTEDA Joins Si2’s Design for Manufacturability Coalition __________________________________9 PTC Holds the Inaugural FIRST Tech Challenge in China to Inspire Student Innovation ______________10 Seven Universities Sign on with Altium: From the -

AMI Import and Export Revision 1, 21 March 2012
Autodesk® Moldflow® Insight 2012 AMI Import and Export Revision 1, 21 March 2012. This document contains Autodesk and third-party software license agreements/notices and/or additional terms and conditions for licensed third-party software components included within the product. These notices and/or additional terms and conditions are made a part of and incorporated by reference into the Autodesk Software License Agreement and/or the About included as part of the Help function within the software. Contents Chapter 1 Supported model import formats. 1 Supported model import formats. 3 Importing a CAD model. 3 Importing an ASCII model file. 3 Importing a model of the core from a CAD program. 4 Importing a Moldflow Plastics Insight 2.0 project. 5 Supported model import formats . 5 Import—Create New Project dialog. 6 Import dialog. 6 Autodesk Moldflow Design Link . 6 Autodesk Moldflow Design Link. 7 Autodesk Moldflow Design Link. 7 Chord angle. 8 Mesh on assembly contact faces. 8 Supported IGES entities. 9 Supported STEP entities. 10 Using models imported from Autodesk Simulation products. 12 Using models imported from Autodesk Simulation products. 13 iii Importing IGES model files. 14 Importing IGES model files. 16 Importing STL model files. 17 Importing STL model files. 19 Importing ANSYS model files. 20 Importing IDEAS universal model files. 20 Importing NASTRAN bulk data model files. 22 Importing PATRAN neutral model files. 22 Importing a C-MOLD *.fem file. 23 Importing a C-MOLD *.fem file. 23 Chapter 2 Exporting models and files. 28 Exporting models and files. 30 Exporting files. 30 Exporting the project to a ZIP file. -

Autodesk® Simulation Moldflow® Comparison Matrix
Autodesk® Simulation Moldflow® Comparison Matrix Autodesk® Simulation Moldflow® injection molding simulation software provides tools that can help manufacturers validate and optimize the design of plastic parts and injection molds and study the injection molding process. Compare the features of Autodesk Simulation Moldflow products to learn how Autodesk® Simulation Moldflow® Adviser and Autodesk® Simulation Moldflow® Insight software can help meet the needs of your organization. Autodesk Autodesk Autodesk Autodesk Autodesk Autodesk Simulation Simulation Simulation Simulation Simulation Simulation Moldflow Moldflow Moldflow Moldflow Moldflow Moldflow LEGEND Adviser Adviser Adviser Insight Insight Insight Feature supported Standard Premium Ultimate Standard Premium Ultimate MESHING TECHNOLOGY Dual Domain™ 3D Midplane CAD INTEROPERABilitY Direct Modeling with Autodesk® Inventor® Fusion Defeaturing with Inventor Fusion Multi-CAD Data Exchange CAD Solid Models Parts Assemblies SimulatiON CapaBilitiES Thermoplastic Filling Part Defects Gate Location Molding Window Thermoplastic Packing Runner Balancing Cooling Warpage Fiber Orientation Insert Overmolding Two-Shot Sequential Overmolding Core Shift Control MOLDING PROCEssES Thermoplastic Injection Molding Reactive Injection Molding Microchip Encapsulation Underfill Encapsulation Gas-Assisted Injection Molding Injection-Compression Molding Co-Injection Molding MuCell® Birefringence -

Manage Engineering Data Complex Models and Simulations Yield a Torrent
NX 8 for Design. Smarter decisions, better products. Learn more on page 11 DtopEng_banner_NXCAD_MAR2012.indd 1 3/8/12 11:02 AM April 2012 / deskeng.com Origin 8.6 Overview P.22 Direct Modeling and FEA P.24 TECHNOLOGY FOR DESIGN ENGINEERING Manage Engineering Data Complex models and simulations yield a torrent of data to seize and control. P.16 RACING AHEAD WITH CLUSTERS P.35 REVIEW: HP Z10 WORKSTATION P.38 P.40 PREPARING 3D MODELS de0412_Cover_Darlene.indd 1 3/15/12 12:20 PM Objet.indd 1 3/14/12 11:17 AM DTE_0412_Layout 1 2/28/12 4:36 PM Page 1 Data Loggers & Data Acquisition Systems iNET-400 Series Expandable Modular Data Acquisition System • Directly Connects to Thermocouple, RTD, Thermistor, Strain Gage, Load Complete Cell, Voltage, Current, Resistance Starter and Accelerometer Inputs System $ • USB 2.0 High Speed Data Acquisition 990 Hardware for Windows® ≥XP SP2, Vista or 7 (XP/VS/7) • Analog and Digital Input and Outputs • Free instruNet World Software Visit omega.com/inet-400_series © Kutt Niinepuu / Dreamstime.com Stand-Alone, High-Speed, 8-Channel High Speed Voltage Multifunction Data Loggers Input USB Data Acquisition Modules OM-USB-1208HS Series Starts at $499 High Performance Multi-Function I/O USB Data Acquisition Modules OMB-DAQ-2416 Series OM-LGR-5320 Series Starts at Starts at $1100 $1499 Visit omega.com/om-lgr-5320_series Visit omega.com/om-usb-1208hs_series Visit omega.com/omb-daq-2416 ® omega.com ® © COPYRIGHT 2012 OMEGA ENGINEERING, INC. ALL RIGHTS RESERVED Omega.indd 1 3/14/12 10:54 AM Degrees of Freedom by Jamie J. -

Finite Element Software for Rubber Products Design
International Journal of Engineering and Management Sciences (IJEMS) Vol. 3. (2018). No. 1. DOI: 10.21791/IJEMS.2018.1.2. Finite Element Software for Rubber Products Design D. HURI Department of Mechanical Engineering, Faculty of Engineering, University of Debrecen, [email protected] Abstract: Automotive rubber products are subjected to large deformations during working conditions, they often contact with other parts and they show highly nonlinear material behavior. Using finite element software for complex analysis of rubber parts can be a good way, although it has to contain special modules. Different types of rubber materials require the curve fitting possibility and the wide range choice of the material models. It is also important to be able to describe the viscoelastic property and the hysteresis. The remeshing possibility can be a useful tool for large deformation and the working circumstances require the contact and self contact ability as well. This article compares some types of the finite element software available on the market based on the above mentioned features. Introduction Finite element simulation of rubber parts is still a demanding task for engineers thanks to the combined effect of several factors. The first one is the elastic modulus of the rubber which depends on the rubber recipe, the shape of the rubber and the size of the deformation as well. The rubber shows nonlinear behavior, therefore the software has to have nonlinear solver ability. While the producers handle the rubber recipe as an industrial secret the mechanical properties have to be determined by laboratory measurements. In most cases the rubber behaves as an elastic, isotropic and nearly incompressible material and it can undergo large deformation. -

DS LLC Engineering AD-12.Vp
Engineering Analysis & Design Wet Electrostatic Precipitator - Temperature, Thermal Expansion, & Stress Autonomous Undersea Vehicle (AUV) Structural Analysis DeepSoft, LLC Engineering Analysis Engineering Analysis & Design TurboSonic, Inc., retained DeepSoft, LLC. (DSL) to provide a detailed Nastran Finite Element Analysis (FEA) of their Wet Electrostatic Precipitators which are shown on the cover. Analyses included heat transfer, thermal expansion & stress, buckling, and structural stress. For Duratek, Inc.'s nuclear waste vitrification melters Algor FEA analyses included heat transfer, thermal expansion and stress, structural stress, and coolant loop pressure drop. Battelle Laboratories required a dynamic modal FEA to determine resonant frequencies, and a dynamic drop impact analysis of their portable ultrasonic cleaner developed for the US Army. For DHS Systems DSL performed a FEA dynamic impact stress analysis of their tow bar for a US Army Ultrasonic Cleaner - Modal Analysis trailer. Some projects may be best served by manual calculations alone without a FEA. Preparation for FEA may involve 20-30 pages of fluid dynamic, thermodynamic, heat transfer, and structural calculations to determine loads, boundary conditions, concentrated mass, and material properties. These are typically automated with Mathcad, Excel, or a C/C++ computer program. Stone Aerospace, developer of the Endurance Autonomous Underwater Vehicle (AUV), retained DSL to create 3D SolidWorks parts, assemblies, and drawings of their science package winch design for a series of Antarctic dives. Inventor or SolidWorks are used for new designs - SpaceClaim allows Nuclear Waste Melter Base - Displacement importing almost any 3D model geometry for design changes or FEA preparation. The principal has also designed a diver propulsion vehicle and a diver's decompression computer. -
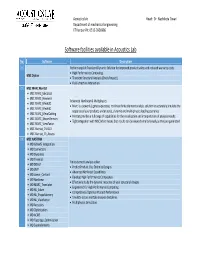
Software Facilities Available in Acoustics Lab
Acoustics lab Head : Dr. Nachiketa Tiwari Department of mechanical engineering IIT Kanpur Ph: 0512‐3926986 Software facilities available in Acoustics Lab No. Software Description 1 Perform explicit Transient Dynamic Solution for improved product safety and reduced warranty costs. High Performance Computing. MSC Dytran Transient Structural Analysis (Crash/Impact) Fluid‐structure Interaction 2 MSC MARC Mentat MSC MARC_Electrical MSC MARC_Hexmesh Advanced Nonlinear & Multiphysics MSC MARC_Mesh2D Marc is a powerful, general‐purpose, nonlinear finite element analysis solution to accurately simulate the MSC MARC_Mesh3D response of your products under static, dynamic and multi‐physics loading scenarios. MSC MARC_MetalCutting Mentat provides a full range of capabilities for the visualization and interpretation of analysis results. MSC MARC_ShapeMemory Tight integration with MSC.Marc means that results can be viewed simultaneously as they are generated. MSC MARC_ViewFactor MSC Mentat_CMOLD MSC Mentat_ITI_Access 3 MSC NASTRAN • MD ADAMS_Integration • MD Connectors • MD Dynamics • MD Thermal Finite element analysis solver. • MD DDAM Predict Product Life, Optimize Designs • MD SMP Advanced Nonlinear Capabilities • MD Linear_Contact Develop High Performance Composites • MD Nonlinear Effectively study the dynamic response of your structural designs • MD MARC_Translator Engineered for High Performance Computing • MD NL_Solver Competitively Optimize Product Performance • MD NL_ShapeMemory Simulate across multiple analysis disciplines -

List of Computational Software
Appendix A List of Computational Software A.1 DICOM Viewers The listed DICOM viewers have similar functionality Acculite www.accuimage.com MicroDicom www.microdicom.com DICOM Works www.dicomworks.com Sante DICOM Viewer www.santesoft.com Mango ric.uthscsa.edu/mango OsiriX (MAC) www.osirix-viewer.com AMIDE amide.sourceforge.net Irfanview www.irfanview.com XNView www.xnview.com A.2 Open Source Medical Imaging and Segmentation CVIPTools A UNIX/Win32-based package and contains a collection of C and C++computer imaging tools that includes edge/line detec- tion, segmentation, and many other functions (www.ee.siue.edu/CVIPtools) Fiji/ImageJ A Java-based image processing package that uses additional plugins for a variety of functionalities including segmentation algorithms (pacific.mpi-cbg.de/wiki/index.php/Fiji) GemIdent An interactive program that is designed for colour segmentation in images with few colours, and the objects of interest look alike with small variation (www.gemident.com) ITK-SNAP An interactive software application that allows users to nav- igate three-dimensional medical images, manually delineate anatomical regions of interest, and perform automatic image segmentation (www.itksnap.org) J. Tu et al., Computational Fluid and Particle Dynamics in the Human Respiratory System, 339 Biological and Medical Physics, Biomedical Engineering DOI 10.1007/978-94-007-4488-2, © Springer Science+Business Media Dordrecht 2013 340 Appendix A List of Computational Software Megawave 2 Made up of C library modules, that contains original algorithms written by researchers and is run using Unix/Linux (megawave.cmla.ens-cachan.fr) MITK and 3Dmed Made up of C++ library for integrated medical image process- ing, segmentation, and registration algorithms (www.mitk.net/download.htm) Slicer Has a GUI that allows manual and automatic segmentation, reg- istration, and three-dimensional visualization. -

With the Best
January 2013 / deskeng.com AMD and NVIDIA Graphic Card Reviews P.40 P.36 Prototype Embedded Systems P.28 Innovations in 3D Scanning TECHNOLOGY FOR DESIGN ENGINEERING FOCUS ON: Test & Mesh Measurement with the Best SCOPING OUT OSCILLOSCOPES P..34 SC12 RECAP P.38 de0113_Cover_Digital.indd 1 12/18/12 2:12 PM Teamcenter end-to-end PLM solutions Great decisions in product lifecycle management #1,509. A product manager adds a customer suggestion to the system… © 2012 Siemens Product Lifecycle Management Software Inc. All rights reserved. Siemens and the Siemens logo are registered registered Management Software Inc. All rights reserved. Siemens and the logo are Lifecycle © 2012 Siemens Product logos, trademarks or serviceowners. All other the propertytrademarks of their respective are of Siemens AG. marks used herein and a CEO adds a new division to the company. Teamcenter: Smarter decisions, better products. Sometimes, the smallest decision in product life cycle management has the greatest impact on a company’s success. Teamcenter PLM solutions from Siemens PLM Software give everyone involved in planning, devel- oping, building and supporting your products the information they need, right when they need it and in the right context to do their job. The result: your entire enterprise collaborates more efficiently, makes smarter more timely decisions— and delivers successful products. Find out how Teamcenter product lifecycle manage- Teamcenter provides a visual user experience to readily see and understand how data is related. ment can help -

PLM Industry Summary Jillian Hayes, Editor Vol
PLM Industry Summary Jillian Hayes, Editor Vol. 15 No 23 Friday 7 June 2013 Contents CIMdata News _____________________________________________________________________ 2 CIMdata Publishes “Focus on Innovation”____________________________________________________2 Optimizing Data Migration and PLM Consolidation: a CIMdata Commentary________________________3 Company News _____________________________________________________________________ 8 Advanced Solutions Awarded Bronze Technical Certification in Autodesk Simulation CFD ____________8 Altair Finalizes Global Partnership with Fujitsu _______________________________________________8 Bentley Issues 2013 Be Inspired Awards Call for Submissions ___________________________________10 Ideate, Inc. Earns Autodesk Civil Infrastructure Specialization ___________________________________11 ITC Infotech Successfully Completes Campus Connect Initiative for PLM Practice __________________12 Lectra Signs a Partnership Contract with Italian Fashion School Polimoda _________________________13 MathWorks to Sponsor RoboCup 2013 _____________________________________________________13 ModernTech Partners with Altium to Provide Electronics Design Software _________________________15 TracePartsOnline.net 3D CAD Library Reaches Out 1.5 Million Users ____________________________15 Events News ______________________________________________________________________ 16 Autodesk to Webcast Its Annual Meeting of Stockholders ______________________________________16 AVEVA and Capgemini Present at Ventyx World 2013 ________________________________________16 -

Torrent Download CFD 2013 32 Bit
Torrent Download CFD 2013 32 Bit ERROR_GETTING_IMAGES-1 Torrent Download CFD 2013 32 Bit 1 / 2 Free Download of ANSYS Student Version. Learn the fundamentals of simulation while gaining experience using our state-of- the-art ANSYS Workbench .... PHOENICS is available compiled as 32-bit, 64-bit and double-precision 64-bit executables. ... If PHOENICS came as a download; start the program phoenics.exe. ... Microsoft MPI (version 10.0.12498.5 supplied); Microsoft Visual C++ 2013 ... software package which uses the techniques of CFD (i.e. Computational Fluid .... Autodesk® CFD software provides flexible fluid flow and thermal simulation tools with improved reliability and performance. Compare ... Download free trial.. Free OpenFOAM® for Windows download now. CFD Software, Easy installation OpenFOAM® for Windows 10, 8, 7. Get. ... Download simFlow Engine (OpenFOAM® for Windows) ... OpenFOAM® 1612+. Download (64-bit) Download (32-bit) .... Be sure to install the correct update (32-bit or 64-bit) for your operating system. ... Windows 32-bit installer - A360 desktop Version 9.1 (exe - 373MB). Windows .... Autodesk Simulation CFD 2013 x64/x86 (2012) Английский ... XP Professional (32-bit: SP3, 64-bit: SP2); Windows Server® 2003, 2008 R2 SP11 ... Internet connection for web downloads and Subscription Aware Access. Farming simulator 2013 rus download mode op. Download configs voor ... Adobe autdition 32 bit torrent download. ... Autodesk simulation cfd torrent download.. This release is built on an updated Xubuntu 16.04.5 LTS 64 bit base and provides updated CAE ... CAELinux 2013 contains updated versions of the Salome_Meca 2013.1 and ... FTP / HTTP / Bittorrent downloads : ... With these software, Open-Source FEA & CFD is continuing its progression towards ease ... -

Abstracts M-Z
14th U.S. National Congress on Computational Mechanics July 17-20, 2017, Montreal, Quebec, Canada Title: Multi-Physics Modeling of Thermomechanical Response of Ultrasonically Activated Soft Tissue Author(s): *Rahul , Suvranu De, Rensselaer Polytechnic Inst.. Ultrasonic surgical instruments have been gaining popularity among surgeons in the last decade. An increasing number of surgical procedures including but not limited to head, neck, gynecological, colorectal and gastrointestinal surgeries are performed using ultrasonic surgical instruments [1]. These instruments utilize ultrasonic vibrations to cut, coagulate and dissect tissues, and seal vessels. They have been proven to be superior to conventional instruments and techniques such as electrosurgical and laser-based devices as they impose lesser thermal injury, desiccation and charring, lower mean blood loss during surgery, no risk of stray current, neuromuscular stimulation, lesser operation time and post-operative pain, and no smoke during the operation to occlude laparoscopic view [2]. Despite the increasing popularity of ultrasound-based surgical procedures, the affects of cellular level mechanisms on the thermomechanical response of ultrasonically activated soft tissues have not been understood completely. We have developed a multi-physics model to investigate the effects of cavitation, due to large transient pressure changes, on the thermomechanical response of soft tissue subjected to ultrasound vibrations [3]. Cellular level cavitation effects have been incorporated in the tissue level continuum model to accurately determine the thermodynamic states such as temperature and pressure. A viscoelastic material model is assumed for the macromechanical response of the tissue. The cavitation model based equation-of-state provides the additional pressure arising from evaporation of intracellular and cellular water by absorbing heat due to viscoelastic heating in the tissue, and temperature to the continuum level thermomechanical model.