Multivariate and Other Worksheets for R (Or S-Plus): a Miscellany
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Accrington Adopted Area Action Plan
ACCRINGTON AT THE HEART OF PENNINE LANCASHIRE HYNDBURN BOROUGH COUNCIL LOCAL DEVELOPMENT FRAMEWORK ACCRINGTON AREA ACTION PLAN PUBLICATION EDITION MARCH 2010 PAGE // Accrington AAP PAGE // Accrington AAP PAGE // Accrington AAP CONTENTS CONTENTS PART A THE PLAN AND ITS CONTEXT Policy Index 1.0 Introduction and Background Plans and Figures .0 Strategic and Local Forward Policy Context .0 Characteristics and Key Issues .0 Vision, Objectives and Proposals Hyndburn Borough Council Planning & Transportation Services Scaitcliffe House Ormerod Street Accrington Lancashire BB5 0PF Tel: 01254 388111 Fax: 01254 391625 [email protected] If you require this information in a different format, for example large print, audio or in different languages please let us know. PAGE // Accrington AAP PART B PART C PART D APPENDICES POLICIES SPATIAL QUARTERS IMPLEMENTATION .0 11.0 1.0 1.0 Range of Uses within the SPATIAL QUARTERS AND IMPLEMENTATION AND APPENDICES Town Centre, Employment PROPOSAL SITE POLICES MONITORING FRAMEWORK Development and Housing The Blackburn Road Quarter Delivering Accrington Appendix 1: Accrington 6.0 Town Centre Area Action Urban Design and Plan Proposal Map Environmental Quality The Arndale Quarter Strategic Business Plan Appendix : Accrington Area 7.0 The Cannon Street Quarter The Town Centre Action Plan: Key Boundaries The Historic Environment Development Board The Grange Quarter Appendix : Policy 8.0 Marketing Strategy ATC: Active Shopping Transport and Access Frontages plan The Scaitcliffe Quarter Performance Indicators -

Cycle Hyndburn
www.lancashire.gov.uk Getting about by bike It couldn’t be easier to get started Jon Sparks British Cycling and Hyndburn CTC, part of Prospects Foundation run comms: 4119 Welcome to the Hyndburn Cycle Map. Hyndburn has a growing network of off-road cycle routes. With more cycle lanes and 20mph zones it is becoming safer to cycle on regular series of cycle rides road too. www.goskyride.com www.prospectsfoundation.org.uk/events/cycling Hyndburn Greenway (Route 6) Hyndburn’s great traffic free route links Blackburn, Accrington and Baxenden. It is part it’s..fun‘n’friendly of national cycle route 6 which will eventually link London with Carlisle Plan your route...Use this map to plan your route. Use quiet roads, the Getting healthier too!... canal towpath or cycle paths, to avoid the worst of the traffic. Baxenden to Accrington Cycling to work or the shops is a way to obtain the 30 minutes a day From Baxenden follow the cycle path on the old railway through the lovely Woodnook It is quicker by bike...Short journeys are often quicker and easier by exercise recommended by doctors. Valley into Accrington bicycle. It is more flexible than public transport and can also be fun. Accrington Causeway Did you know Cycling?.. Cross the lake into Accrington Town Centre on the unique causeway. The red pillars • Keeps you young ...Regular cyclists are as fit as an average person 10 used to carry the railway across the lake. The lake supplied the Globe Works which years younger. was the largest textile machinery works in the world. -

NOTICE of POLL Election of a County Councillor
NOTICE OF POLL Lancashire County Council Election of a County Councillor for Accrington North Notice is hereby given that: 1. A poll for the election of a County Councillor for Accrington North will be held on Thursday 6 May 21, between the hours of 7:00 am and 10:00 pm. 2. The number of County Councillors to be elected is one. 3. The names, home addresses and descriptions of the Candidates remaining validly nominated for election and the names of all persons signing the Candidates nomination paper are as follows: Names of Signatories Name of Candidate Home Address Description (if any) Proposers(+), Seconders(++) & Assentors COX 27 Pansy Street South, Labour Party Paul I Cox (+) Rebecca Mcinroy (++) Loraine Accrington, Lancashire, BB5 4BS HARRIS 4 Ward Avenue, UKIP Oliver M J Walsh (+) Thomas M J Walsh (++) Len Oswaldtwistle, Accrington, Lancashire, BB5 3NP MAHMOOD 344 Blackburn Road, Conservative Party Talib H Zaman (+) Trevor J Dawson (++) Shahed Accrington, Candidate Lancashire, BB5 1RZ WEST Lyndene, Blackburn Green Party Peter Billington (+) Anne Billington (++) Joan Elizabeth Old Road, Great Harwood, BB6 7UW 4. The situation of Polling Stations and the description of persons entitled to vote thereat are as follows: Station Ranges of electoral register numbers of Situation of Polling Station Number persons entitled to vote thereat Huncoat Primary School, Lynwood Road, Huncoat, Accrington 1 AA-1 to AA-928 St Augustines Church, Bolton Avenue, Huncoat 2 AB-1 to AB-1593 St Johns Church Vestry, Addison Street, Accrington 4 BA-30 to BA-583 Lupin Road Community, Centre, Lupin Road, Accrington 15 ED-1 to ED-303 Lupin Road Community, Centre, Lupin Road, Accrington 15 GC-1 to GC-736 St. -

Crime Reduction & Community Safety Group Tilley Awards 2008 Application Form Please Ensure That You Have Read the Guidance B
Crime Reduction & Community Safety Group Tilley Awards 2008 Application form Please ensure that you have read the guidance before completing this form. By making an application to the awards, entrants are agreeing to abide by the conditions laid out in the guidance. Please complete the following form in full, within the stated word limit and ensuring the file size is no more than 1MB. Failure to do so will result in your entry being rejected from the competition. Completed application forms should be e-mailed to [email protected]. All entries must be received by noon on Friday 25th April 2008. No entries will be accepted after this time/date. Any queries on the application process should be directed to Alex Blackwell on 0207 035 4811. Section A: Application basics 1. Title of the project: ABBA – Accrington Bonfire Behavioural Attitudes 2. Key issue that the project is addressing: Irresponsible Behaviour Author contact details 3. Name of application author: M. Frankland 4. Organisation submitting the application: LFRS 5. Full postal address: Lancashire Fire & Rescue Service Eastern Area Headquarters Hyndburn Road, Church, BB5 4EQ 6. Email address: [email protected] 7. Telephone number: 01254 356988 Secondary project contact details 8. Name of secondary contact involved in the project: Ian Potter 9. Secondary contact email address: [email protected] 10. Secondary contact telephone number: 01282 423240 ABBA Page 1 of 3 Endorsing representative contact details 11. Name of endorsing senior representative from lead Organisation: AM Aspden 12. Endorsing representative’s email address: [email protected] 13. For all entries from England & Wales please state which Government Office or Welsh Assembly Government your organisation is covered by e.g. -

Local Government Boundary Commission for England Report No
Local Government Boundary Commission For England Report No. 67 LOCAL GOVERNMENT BOUNDARY COMMISSION FOR ENGLAND RETORT NO. b"7 LOCAL GOVERNMENT BOUNDARY COMMISSION FOR ENGLAND CHAIRMAN Sir Edmund Compton, GCB.KBE. DEPUTY CHAIRMAN Mr J M Rankin,QC. MEMBERS The Countess Of Albemarle, DBE. Mr 0? C Benfield. Professor Michael Chisholm. Sir Andrew Wheatley,CBE. Mr P B Young, CBE. PH To the Rt Hon Roy. Jenkins MF Secretary of State for the Home -Department PROPOSALS FOR REVISED ELECTORAL ARRANGEMENTS FOR THE BOROUGH OF HYNDBURN IN THE COUNTY OF LANCASHIRE 1. We, the Local Government Boundary Commission for England, having carried out our initial review of the electoral arrangements for the borough of Hyndburn in accordance with the requirements of section 63 and Schedule 9 to the Local Government Act 1972, present our proposals for the future electoral arrangements for that borough. 2. In accordance with the procedure laid down in section 60 (1) and (2) of the 1972 Act, notice was given on 13 May 197^ that we were to undertake this review. This was incorporated in a consultation letter addressed to the Kyndburn Borough Council, copies of which were circulated to the Lancashire County Council, the Altham Parish Council, the Members of Parliament for the constituencies concerned and the headquarters of the main political parties,. Copies v/ere also sent to the editors of the local newspapers circulating ir. the area and.to the local government press. Notices inserted in the local press announced the start of the review and invited comments from members of the public and from any interested bodies. -
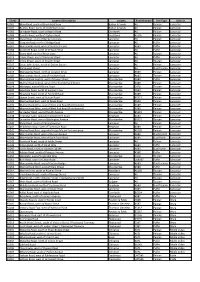
Siteid Location Description Locality Road Number Site Type District
SiteID Location Description Locality Road Number Site Type District A5001 Main Road, south of Brookfield View Bolton le Sands A6 Pelican Lancaster A5002 By Pass Road, north of St Michaels Lane Bolton le Sands A6 Pelican Lancaster A5003 Lancaster Road, south of North Road Carnforth A6 Pelican Lancaster A5004 Coastal Road, north of Station Road Hest Bank A5105 Pelican Lancaster A5005 Slyne Road, south of Barley Cop Lane Lancaster A6 Pelican Lancaster A5006 Greaves Road, north of Bridge Road Lancaster A6 Puffin Lancaster A5007 Morecambe Road, west of Scale Hall Lane Lancaster A683 Puffin Lancaster A5008 Scotforth Road, north of St Pauls Road Lancaster A6 Puffin Lancaster A5012 Stone Well, north of Moor Lane Lancaster A6 Toucan Lancaster A5013 Cable Street, east of Damside Street Lancaster A6 Puffin Lancaster A5014 China Street, south of Church Street Lancaster A6 Toucan Lancaster A5015 Great John Street, north of Dalton Square Lancaster A6 Pelican Lancaster A5016 Parliament Street Lancaster A6 Dual Toucan Lancaster A5019 Morecambe Road, north of Longton Drive Lancaster A589 Pelican Lancaster A5020 Morecambe Road, east of Penrhyn Road Lancaster A683 Toucan Lancaster A5022 Marine Road Central, west of Queen Street Morecambe A589 Puffin Lancaster A5026 Marine Road Central, west of Northumberland Street Morecambe A589 Pelican Lancaster A5028 Westgate, east of Altham Road Morecambe C470 Toucan Lancaster A5029 Heysham Road, north of Sugham Lane Morecambe A589 Pelican Lancaster A5030 Heysham Road, north of Fairfield Road Morecambe A589 Pelican -

2001 No. 2469 LOCAL GOVERNMENT, ENGLAND The
STATUTORY INSTRUMENTS 2001 No. 2469 LOCAL GOVERNMENT, ENGLAND The Borough of Hyndburn (Electoral Changes) Order 2001 Made ----- 3rdJuly 2001 Coming into force in accordance with article 1(2) Whereas the Local Government Commission for England, acting pursuant to section 15(4) of the Local Government Act 1992(a), has submitted to the Secretary of State a report dated September 2000 on its review of the borough(b) of Hyndburn together with its recommendations: And whereas the Secretary of State has decided to give effect to those recommendations: Now, therefore, the Secretary of State, in exercise of the powers conferred on him by sections 17(c) and 26 of the Local Government Act 1992, and of all other powers enabling him in that behalf, hereby makes the following Order: Citation, commencement and interpretation 1.—(1) This Order may be cited as the Borough of Hyndburn (Electoral Changes) Order 2001. (2) This Order shall come into force— (a) for the purpose of proceedings preliminary or relating to any election to be held on 2nd May 2002, on 15th October 2001; (b) for all other purposes, on 2nd May 2002. (3) In this Order— “borough” means the borough of Hyndburn; “existing”, in relation to a ward, means the ward as it exists on the date this Order is made; and any reference to the map is a reference to the map prepared by the Department for Transport, Local Government and the Regions marked “Map of the Borough of Hyndburn (Electoral Changes) Order 2001”, and deposited in accordance with regulation 27 of the Local Government Changes for England Regulations 1994(d). -
Hyndburn Borough Council Election Results 1973-2012
Hyndburn Borough Council Election Results 1973-2012 Colin Rallings and Michael Thrasher The Elections Centre Plymouth University The information contained in this report has been obtained from a number of sources. Election results from the immediate post-reorganisation period were painstakingly collected by Alan Willis largely, although not exclusively, from local newspaper reports. From the mid- 1980s onwards the results have been obtained from each local authority by the Elections Centre. The data are stored in a database designed by Lawrence Ware and maintained by Brian Cheal and others at Plymouth University. Despite our best efforts some information remains elusive whilst we accept that some errors are likely to remain. Notice of any mistakes should be sent to [email protected]. The results sequence can be kept up to date by purchasing copies of the annual Local Elections Handbook, details of which can be obtained by contacting the email address above. Front cover: the graph shows the distribution of percentage vote shares over the period covered by the results. The lines reflect the colours traditionally used by the three main parties. The grey line is the share obtained by Independent candidates while the purple line groups together the vote shares for all other parties. Rear cover: the top graph shows the percentage share of council seats for the main parties as well as those won by Independents and other parties. The lines take account of any by- election changes (but not those resulting from elected councillors switching party allegiance) as well as the transfers of seats during the main round of local election. -

2011-12 Annual Report
The PROSPECTS Foundation Hyndburn’s community-owned environmental charity The PROSPECTS Foundation is an environmental charity, established by Hyndburn people in 1998, to help improve the quality of life for all Hyndburn communities and contribute local-level solutions to wider environmental problems. We achieve this through a supported network of groups and by working in innovative ways with a diverse range of organisations and partners for environmental, social and economic benefits. Our Mission To be the key movement in Hyndburn for environmental sustainability and to use our collective knowledge, skills, work and experience to secure this for current and future generations. Our Values: • We value our environment, both local and global, and respect its uniqueness and fragility. • We are committed to the principle of environmental sustainability. • We act as a catalyst for positive environmental change. • We believe in working collaboratively for our environment. • We believe that local people acting in their own right or collectively can reduce their carbon footprints by changing their behaviour and practices. • We are a people based organisation which is rooted in local communities. • We seek to work for the benefit of all communities both present and future. • We believe everyone has a positive contribution to make and we are committed to equality of opportunity for all. • We work ethically. Our Themes of Sustainability We focus on projects which meet our Themes of Sustainability. These themes take account of both the local and global -

The Influence of Railways on the Development of Accrington and District, 1848-1914
THE INFLUENCE OF RAILWAYS ON THE DEVELOPMENT OF ACCRINGTON AND DISTRICT, 1848-1914 .1 • I • t•1 "I •I BY MARK ALAN HAYDOCK, BA., M.A. A THESIS SUBMI1TED IN PARTIAL FULFILMENT FOR THE REQUIREMENTS FOR THE DEGREE OF DOCTOR OF PHILOSOPHY AT THE UNIVERSITY OF CENTRAL LANCASHIRE July 2009 University of Central Lancashire Student Declaration Concurrent registration for two or more academic awards Either *1 declare that while registered as a candidate for the research degree, I have not been a registered candidate or enrolled student for another award of the University or other academic or professional institution or *1 declare that while registered for the research degree, I was with the University's specific permission, a *registered candidaterenrolled student for the following award: Material submitted for another award Either *1 declare that no material contained in the thesis has been used in any other submission for an academic award and is solely my own work. or I declare that the following material contained in the thesis formed part of a submission for the award of (state award and awarding body and list the material below): Collaboration Where a candidates research programme is part of a collaborative project, the thesis must indicate in addition clearly the candidate's individual contribution and the extent of the collaboration. Please state below Signature of Candidate Type of Award PA tO - r r 1 p School ABSTRACT OF THESIS The project explores the complex and counter-intuitive historical relationships between railways and development through a local study of Accrington and the surrounding smaller towns and townships in East Lancashire. -

2009-10 Annual Report
The PROSPECTS Foundation Hyndburn's community-owned environmental charity The PROSPECTS Foundation is an environmental charity, established by Hyndburn people in 1998, to help improve the quality of life for all Hyndburn communities and contribute local-level solutions to wider environmental problems. We achieve this through a supported network of groups and by working in innovative ways with a diverse range of organisations and partners for environmental, social and economic benefits. Our Mission To be the key movement in Hyndburn for environmental sustainability and to use our collective knowledge, skills, work and experience to secure this for current and future generations. Our Values: - We value our environment, both local and global, and respect its uniqueness and fragility. - We are committed to the principle of environmental sustainability. - We act as a catalyst for positive environmental change. - We believe in working collaboratively for our environment. - We believe that local people acting in their own right or collectively can reduce their carbon footprints by changing their behaviour and practices. - We are a people based organisation which is rooted in local d communities. - We seek to work for the benefit of all communities both present r and future. - We believe everyone has a positive contribution to make and we o are committed to equality of opportunity for all. - We work ethically. w Our Five Themes of Sustainability We focus on projects which meet our Five Themes of Sustainability. These e themes take account of both the local and global environment, and con- tribute to the mitigation of climate change. r Biodiversity - Protecting and enhancing local wildlife and plant life o Energy - Home and community energy efficiency and use of renewables Sustainable Transport - Encouraging cycling, walking and public transport F Waste and Recycling - Reducing, reusing and recycling our waste Local Food - Growing more local, organic, healthy food, grown by the community for the community. -

Final Recommendations on the Future Electoral Arrangements for Hyndburn in Lancashire
Final recommendations on the future electoral arrangements for Hyndburn in Lancashire Report to the Secretary of State for the Environment, Transport and the Regions September 2000 LOCAL GOVERNMENT COMMISSION FOR ENGLAND LOCAL GOVERNMENT COMMISSION FOR ENGLAND This report sets out the Commission’s final recommendations on the electoral arrangements for the borough of Hyndburn in Lancashire. Members of the Commission are: Professor Malcolm Grant (Chairman) Professor Michael Clarke CBE (Deputy Chairman) Peter Brokenshire Kru Desai Pamela Gordon Robin Gray Robert Hughes CBE Barbara Stephens (Chief Executive) © Crown Copyright 2000 Applications for reproduction should be made to: Her Majesty’s Stationery Office Copyright Unit. The mapping in this report is reproduced from OS mapping by the Local Government Commission for England with the permission of the Controller of Her Majesty’s Stationery Office, © Crown Copyright. Unauthorised reproduction infringes Crown Copyright and may lead to prosecution or civil proceedings. Licence Number: GD 03114G. This report is printed on recycled paper. Report no: 176 ii LOCAL GOVERNMENT COMMISSION FOR ENGLAND CONTENTS page LETTER TO THE SECRETARY OF STATE v SUMMARY vii 1 INTRODUCTION 1 2 CURRENT ELECTORAL ARRANGEMENTS 5 3 DRAFT RECOMMENDATIONS 9 4 RESPONSES TO CONSULTATION 11 5 ANALYSIS AND FINAL RECOMMENDATIONS 13 6 NEXT STEPS 25 A large map illustrating the proposed ward boundaries for Hyndburn is inserted inside the back cover of the report. LOCAL GOVERNMENT COMMISSION FOR ENGLAND iii iv LOCAL GOVERNMENT COMMISSION FOR ENGLAND Local Government Commission for England 5 September 2000 Dear Secretary of State On 7 September 1999 the Commission began a periodic electoral review of Hyndburn under the Local Government Act 1992.