DOCSLIB.ORG

Proof of Intersection of a Line and a Circle

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Proof of Intersection of a Line and a Circle Proof of Intersection of a Line and a Circle P2(x2,y2) P1(x1,y1) r C(xc,yc) This problem is most easily solved if the circle is in implicit form: 2 2 2 (x − xc) + (y − yc) − r = 0 and the line is parametric: x = x0 + ft y = y0 + gt Substituting for (parametric line) x and y into the circle equation gives a quadratic equation in t: • Two roots of which give points on the line where cuts the circle. p f(x − x ) + g(y − y ) ± r2(f 2 + g2) − (f(y − y ) − g(x − x ))2 t = c 0 c 0 c 0 c 0 (f 2 + g2) • The roots maybe coincident if the line is tangential to the circle. P1(x1,y1) 1 r C(xc,yc) • If roots are imaginary then there is no intersection. 1 1 Proof: The circle is in implicit form: 2 2 2 (x − xc) + (y − yc) − r = 0 (1) and the line is parametric: x = x0 + ft y = y0 + gt (2) Substituting for (parametric line) x and y from Eqn. 2 into the circle equation, Eqn. 1, gives a quadratic equation in t gives: 2 2 2 (x0 + ft − xc) + (y0 + gt − yc) − r = 0 (3) Let xd = x0 − xc yd = y0 − yc (4) Then we may write Eqn. 3 2 2 2 (xd + ft) + (yd + gt) − r = 0 (5) Expanding the quadratic parts in Eqn. 5 gives: 2 2 2 2 2 2 2 xd + 2fxdt + f t + yd + 2gydt + g t − r = 0 (6) Express Eqn. 6 as a quadratic in t, so gather terms in t in Eqn. 6: 2 2 2 2 2 2 (f + g )t + (2fxd + 2gyd)t + xd + yd − r = 0 2 2 2 2 2 2 (f + g )t + 2(fxd + gyd)t + xd + yd − r = 0 (7) 2 2 Now the general solution of a quadratic of the form ax + bx + c = 0, gives the roots, xi; i = 1; 2 as: p −b ± b2 − 4ac x = (8) i 2a So in our problem (a quadratic in t) from Eqn. 7 we can see that for Eqn. 8: a = (f 2 + g2) b = 2(fxd + gyd) 2 2 2 c = xd + yd − r Substituting for a; b and c in Eqn. 8 we get roots of t, ti: q 2 2 2 2 2 2 −2(fxd + gyd) ± (2(fxd + gyd)) − 4(xd + yd − r )(f + g ) t = i 2(f 2 + g2) q 2 2 2 2 2 2 −2(xd + gyd) ± 4(fxd + gyd) − 4(xd + yd − r )(f + g ) t = i 2(f 2 + g2) (9) The expression of the right hand side of Eqn. 9 can be simplified in a few ways. p Firstly we can factor 4 from the term and the division by 2 then simplifies the equation to: q 2 2 2 2 2 2 −2(xd + gyd) ± 2 (fxd + gyd) − (xd + yd − r )(f + g ) t = i 2(f 2 + g2) q 2 2 2 2 2 2 −(fxd + gyd) ± (fxd + gyd) − (xd + yd − r )(f + g ) t = i (f 2 + g2) (10) 3 p Let us now consider the term and simplify this, let: 2 2 2 2 2 2 S = (fxd + gyd) − (xd + yd − r )(f + g )) 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 S = f xd + 2fgxdyd + g yd − f xd − f yd + f r − g xd − g yd + g r (11) 2 2 2 2 Eqn 11 can be simplified as follows, some terms cancel out f xd, g yd and others can be gathered together r2; f; and g terms: 2 2 2 2 2 2 2 S = r (f + g ) − (f yd − 2fgxdyd + g xd 2 2 2 2 S = r (f + g ) − (fyd − gxd) 2 2 2 2 S = r (f + g ) − (−gxd + fyd) (12) Substituting for xd and yd from Eqn. 4 in Eqn 12 we get: 2 2 2 2 S = r (f + g ) − (−g(x0 − xc) + f(y0 − yc)) 2 2 2 2 S = r (f + g ) − (g(xc − x0) − f(yc − y0)) p Substituting for S from Eqn. 13 and xd and yd from Eqn. 4 in the term in Eqn. 10 gives us the solution: p f(x − x ) + g(y − y ) ± r2(f 2 + g2) − (f(y − y ) − g(x − x ))2 t = c 0 c 0 c 0 c 0 (f 2 + g2) Q.E.D 4.
Load more

Recommended publications
  • Proofs with Perpendicular Lines
    3.4 Proofs with Perpendicular Lines EEssentialssential QQuestionuestion What conjectures can you make about perpendicular lines? Writing Conjectures Work with a partner. Fold a piece of paper D in half twice. Label points on the two creases, as shown. a. Write a conjecture about AB— and CD — . Justify your conjecture. b. Write a conjecture about AO— and OB — . AOB Justify your conjecture. C Exploring a Segment Bisector Work with a partner. Fold and crease a piece A of paper, as shown. Label the ends of the crease as A and B. a. Fold the paper again so that point A coincides with point B. Crease the paper on that fold. b. Unfold the paper and examine the four angles formed by the two creases. What can you conclude about the four angles? B Writing a Conjecture CONSTRUCTING Work with a partner. VIABLE a. Draw AB — , as shown. A ARGUMENTS b. Draw an arc with center A on each To be prof cient in math, side of AB — . Using the same compass you need to make setting, draw an arc with center B conjectures and build a on each side of AB— . Label the C O D logical progression of intersections of the arcs C and D. statements to explore the c. Draw CD — . Label its intersection truth of your conjectures. — with AB as O. Write a conjecture B about the resulting diagram. Justify your conjecture. CCommunicateommunicate YourYour AnswerAnswer 4. What conjectures can you make about perpendicular lines? 5. In Exploration 3, f nd AO and OB when AB = 4 units.
    [Show full text]
  • Some Intersection Theorems for Ordered Sets and Graphs
    IOURNAL OF COMBINATORIAL THEORY, Series A 43, 23-37 (1986) Some Intersection Theorems for Ordered Sets and Graphs F. R. K. CHUNG* AND R. L. GRAHAM AT&T Bell Laboratories, Murray Hill, New Jersey 07974 and *Bell Communications Research, Morristown, New Jersey P. FRANKL C.N.R.S., Paris, France AND J. B. SHEARER' Universify of California, Berkeley, California Communicated by the Managing Editors Received May 22, 1984 A classical topic in combinatorics is the study of problems of the following type: What are the maximum families F of subsets of a finite set with the property that the intersection of any two sets in the family satisfies some specified condition? Typical restrictions on the intersections F n F of any F and F’ in F are: (i) FnF’# 0, where all FEF have k elements (Erdos, Ko, and Rado (1961)). (ii) IFn F’I > j (Katona (1964)). In this paper, we consider the following general question: For a given family B of subsets of [n] = { 1, 2,..., n}, what is the largest family F of subsets of [n] satsifying F,F’EF-FnFzB for some BE B. Of particular interest are those B for which the maximum families consist of so- called “kernel systems,” i.e., the family of all supersets of some fixed set in B. For example, we show that the set of all (cyclic) translates of a block of consecutive integers in [n] is such a family. It turns out rather unexpectedly that many of the results we obtain here depend strongly on properties of the well-known entropy function (from information theory).
    [Show full text]
  • Complete Intersection Dimension
    PUBLICATIONS MATHÉMATIQUES DE L’I.H.É.S. LUCHEZAR L. AVRAMOV VESSELIN N. GASHAROV IRENA V. PEEVA Complete intersection dimension Publications mathématiques de l’I.H.É.S., tome 86 (1997), p. 67-114 <http://www.numdam.org/item?id=PMIHES_1997__86__67_0> © Publications mathématiques de l’I.H.É.S., 1997, tous droits réservés. L’accès aux archives de la revue « Publications mathématiques de l’I.H.É.S. » (http:// www.ihes.fr/IHES/Publications/Publications.html) implique l’accord avec les conditions géné- rales d’utilisation (http://www.numdam.org/conditions). Toute utilisation commerciale ou im- pression systématique est constitutive d’une infraction pénale. Toute copie ou impression de ce fichier doit contenir la présente mention de copyright. Article numérisé dans le cadre du programme Numérisation de documents anciens mathématiques http://www.numdam.org/ COMPLETE INTERSECTION DIMENSION by LUGHEZAR L. AVRAMOV, VESSELIN N. GASHAROV, and IRENA V. PEEVA (1) Abstract. A new homological invariant is introduced for a finite module over a commutative noetherian ring: its CI-dimension. In the local case, sharp quantitative and structural data are obtained for modules of finite CI- dimension, providing the first class of modules of (possibly) infinite projective dimension with a rich structure theory of free resolutions. CONTENTS Introduction ................................................................................ 67 1. Homological dimensions ................................................................... 70 2. Quantum regular sequences ..............................................................
    [Show full text]
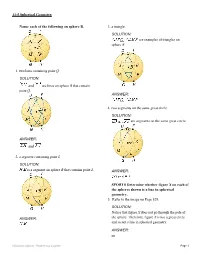
  • And Are Lines on Sphere B That Contain Point Q
    11-5 Spherical Geometry Name each of the following on sphere B. 3. a triangle SOLUTION: are examples of triangles on sphere B. 1. two lines containing point Q SOLUTION: and are lines on sphere B that contain point Q. ANSWER: 4. two segments on the same great circle SOLUTION: are segments on the same great circle. ANSWER: and 2. a segment containing point L SOLUTION: is a segment on sphere B that contains point L. ANSWER: SPORTS Determine whether figure X on each of the spheres shown is a line in spherical geometry. 5. Refer to the image on Page 829. SOLUTION: Notice that figure X does not go through the pole of ANSWER: the sphere. Therefore, figure X is not a great circle and so not a line in spherical geometry. ANSWER: no eSolutions Manual - Powered by Cognero Page 1 11-5 Spherical Geometry 6. Refer to the image on Page 829. 8. Perpendicular lines intersect at one point. SOLUTION: SOLUTION: Notice that the figure X passes through the center of Perpendicular great circles intersect at two points. the ball and is a great circle, so it is a line in spherical geometry. ANSWER: yes ANSWER: PERSEVERANC Determine whether the Perpendicular great circles intersect at two points. following postulate or property of plane Euclidean geometry has a corresponding Name two lines containing point M, a segment statement in spherical geometry. If so, write the containing point S, and a triangle in each of the corresponding statement. If not, explain your following spheres. reasoning. 7. The points on any line or line segment can be put into one-to-one correspondence with real numbers.
    [Show full text]
  • Intersection of Convex Objects in Two and Three Dimensions
    Intersection of Convex Objects in Two and Three Dimensions B. CHAZELLE Yale University, New Haven, Connecticut AND D. P. DOBKIN Princeton University, Princeton, New Jersey Abstract. One of the basic geometric operations involves determining whether a pair of convex objects intersect. This problem is well understood in a model of computation in which the objects are given as input and their intersection is returned as output. For many applications, however, it may be assumed that the objects already exist within the computer and that the only output desired is a single piece of data giving a common point if the objects intersect or reporting no intersection if they are disjoint. For this problem, none of the previous lower bounds are valid and algorithms are proposed requiring sublinear time for their solution in two and three dimensions. Categories and Subject Descriptors: E.l [Data]: Data Structures; F.2.2 [Analysis of Algorithms]: Nonnumerical Algorithms and Problems General Terms: Algorithms, Theory, Verification Additional Key Words and Phrases: Convex sets, Fibonacci search, Intersection 1. Introduction This paper describes fast algorithms for testing the predicate, Do convex objects P and Q intersect? where an object is taken to be a line or a polygon in two dimensions or a plane or a polyhedron in three dimensions. The related problem Given convex objects P and Q, compute their intersection has been well studied, resulting in linear lower bounds and linear or quasi-linear upper bounds [2, 4, 11, 15-171. Lower bounds for this problem use arguments This research was supported in part by the National Science Foundation under grants MCS 79-03428, MCS 81-14207, MCS 83-03925, and MCS 83-03926, and by the Defense Advanced Project Agency under contract F33615-78-C-1551, monitored by the Air Force Offtce of Scientific Research.
    [Show full text]
  • Complex Intersection Bodies
    COMPLEX INTERSECTION BODIES A. KOLDOBSKY, G. PAOURIS, AND M. ZYMONOPOULOU Abstract. We introduce complex intersection bodies and show that their properties and applications are similar to those of their real counterparts. In particular, we generalize Busemann's the- orem to the complex case by proving that complex intersection bodies of symmetric complex convex bodies are also convex. Other results include stability in the complex Busemann-Petty problem for arbitrary measures and the corresponding hyperplane inequal- ity for measures of complex intersection bodies. 1. Introduction The concept of an intersection body was introduced by Lutwak [37], as part of his dual Brunn-Minkowski theory. In particular, these bodies played an important role in the solution of the Busemann-Petty prob- lem. Many results on intersection bodies have appeared in recent years (see [10, 22, 34] and references there), but almost all of them apply to the real case. The goal of this paper is to extend the concept of an intersection body to the complex case. Let K and L be origin symmetric star bodies in Rn: Following [37], we say that K is the intersection body of L if the radius of K in every direction is equal to the volume of the central hyperplane section of L perpendicular to this direction, i.e. for every ξ 2 Sn−1; −1 ? kξkK = jL \ ξ j; (1) ? n where kxkK = minfa ≥ 0 : x 2 aKg, ξ = fx 2 R :(x; ξ) = 0g; and j · j stands for volume. By a theorem of Busemann [8] the intersection body of an origin symmetric convex body is also convex.
    [Show full text]
  • Points, Lines, and Planes a Point Is a Position in Space. a Point Has No Length Or Width Or Thickness
    Points, Lines, and Planes A Point is a position in space. A point has no length or width or thickness. A point in geometry is represented by a dot. To name a point, we usually use a (capital) letter. A A (straight) line has length but no width or thickness. A line is understood to extend indefinitely to both sides. It does not have a beginning or end. A B C D A line consists of infinitely many points. The four points A, B, C, D are all on the same line. Postulate: Two points determine a line. We name a line by using any two points on the line, so the above line can be named as any of the following: ! ! ! ! ! AB BC AC AD CD Any three or more points that are on the same line are called colinear points. In the above, points A; B; C; D are all colinear. A Ray is part of a line that has a beginning point, and extends indefinitely to one direction. A B C D A ray is named by using its beginning point with another point it contains. −! −! −−! −−! In the above, ray AB is the same ray as AC or AD. But ray BD is not the same −−! ray as AD. A (line) segment is a finite part of a line between two points, called its end points. A segment has a finite length. A B C D B C In the above, segment AD is not the same as segment BC Segment Addition Postulate: In a line segment, if points A; B; C are colinear and point B is between point A and point C, then AB + BC = AC You may look at the plus sign, +, as adding the length of the segments as numbers.
    [Show full text]
  • INTERSECTION GEOMETRY Learning Outcomes
    INTERSECTION GEOMETRY Learning Outcomes 5-2 At the end of this module, you will be able to: 1. Explain why tight/right angle intersections are best 2. Describe why pedestrians need access to all corners 3. Assess good crosswalk placement: where peds want to cross & where drivers can see them 4. Explain how islands can break up complex intersections Designing for Pedestrian Safety – Intersection Geometry Intersection Crashes Some basic facts: 5-3 1. Most (urban) crashes occur at intersections 2. 40% occur at signalized intersections 3. Most are associated with turning movements 4. Geometry matters: keeping intersections tight, simple & slow speed make them safer for everyone Designing for Pedestrian Safety – Intersection Geometry 5-4 Philadelphia PA Small, tight intersections best for pedestrians… Simple, few conflicts, slow speeds Designing for Pedestrian Safety – Intersection Geometry 5-5 Atlanta GA Large intersections can work for pedestrians with mitigation Designing for Pedestrian Safety – Intersection Geometry Skewed intersections 5-6 Skew increases crossing distance & speed of turning cars Designing for Pedestrian Safety – Intersection Geometry 5-7 Philadelphia PA Cars can turn at high speed Designing for Pedestrian Safety – Intersection Geometry 5-8 Skew increases crosswalk length, decreases visibility Designing for Pedestrian Safety – Intersection Geometry 5-9 Right angle decreases crosswalk length, increases visibility Designing for Pedestrian Safety – Intersection Geometry 5-10 Bend OR Skewed intersection reduces visibility Driver
    [Show full text]
  • On Geometric Intersection of Curves in Surfaces
    GEOMETRIC INTERSECTION OF CURVES ON SURFACES DYLAN P. THURSTON This is a pre-preprint. Please give comments! Abstract. In order to better understand the geometric inter- section number of curves, we introduce a new tool, the smooth- ing lemma. This lets us write the geometric intersection number i(X, A), where X is a simple curve and A is any curve, canonically as a maximum of various i(X, A′), where the A′ are also simple and independent of X. We use this to get a new derivation of the change of Dehn- Thurston coordinates under an elementary move on the pair of pants decomposition. Contents 1. Introduction 2 1.1. Acknowledgements 3 2. Preliminaries on curves 3 3. Smoothing curves 4 4. Dehn-Thurston coordinates 8 4.1. Generalized coordinates 10 5. Twisting of curves 11 5.1. Comparing twisting 13 5.2. Twisting around multiple curves 14 6. Fundamental pants move 14 7. Convexity of length functions 18 Appendix A. Elementary moves 20 Appendix B. Comparison to Penner’s coordinates 20 References 20 Key words and phrases. Dehn coordinates,curves on surfaces,tropical geometry. 1 2 THURSTON 1. Introduction In 1922, Dehn [2] introduced what he called the arithmetic field of a surface, by which he meant coordinates for the space of simple curves on a surface, together with a description for how to perform a change of coordinates. In particular, this gives the action of the mapping class group of the surface. He presumably chose the name “arithmetic field” because in the simplest non-trivial cases, namely the torus, the once- punctured torus, and the 4-punctured sphere, the result is equivalent to continued fractions and Euler’s method for finding the greatest common divisor.
    [Show full text]
  • Intersection Geometric Design
    Intersection Geometric Design Course No: C04-033 Credit: 4 PDH Gregory J. Taylor, P.E. Continuing Education and Development, Inc. 22 Stonewall Court Woodcliff Lake, NJ 07677 P: (877) 322-5800 [email protected] Intersection Geometric Design INTRODUCTION This course summarizes and highlights the geometric design process for modern roadway intersections. The contents of this document are intended to serve as guidance and not as an absolute standard or rule. When you complete this course, you should be familiar with the general guidelines for at-grade intersection design. The course objective is to give engineers and designers an in-depth look at the principles to be considered when selecting and designing intersections. Subjects include: 1. General design considerations – function, objectives, capacity 2. Alignment and profile 3. Sight distance – sight triangles, skew 4. Turning roadways – channelization, islands, superelevation 5. Auxiliary lanes 6. Median openings – control radii, lengths, skew 7. Left turns and U-turns 8. Roundabouts 9. Miscellaneous considerations – pedestrians, traffic control, frontage roads 10. Railroad crossings – alignments, sight distance For this course, Chapter 9 of A Policy on Geometric Design of Highways and Streets (also known as the “Green Book”) published by the American Association of State Highway and Transportation Officials (AASHTO) will be used primarily for fundamental geometric design principles. This text is considered to be the primary guidance for U.S. roadway geometric design. Copyright 2015 Gregory J. Taylor, P.E. Page 2 of 56 Intersection Geometric Design This document is intended to explain some principles of good roadway design and show the potential trade-offs that the designer may have to face in a variety of situations, including cost of construction, maintenance requirements, compatibility with adjacent land uses, operational and safety impacts, environmental sensitivity, and compatibility with infrastructure needs.
    [Show full text]
  • Don't Give up at the Intersection
    Don’t Give Up at the Intersection Designing All Ages and Abilities Bicycle Crossings May 2019 NACTO Executive Board Working Group NACTO Project Team Janette Sadik-Khan Cara Seiderman Corinne Kisner Principal, Bloomberg Community Development Executive Director Associates Department, Cambridge, MA NACTO Chair Kate Fillin-Yeh Ted Wright Director of Strategy Seleta Reynolds New York City Department of General Manager, Los Angeles Transportation Nicole Payne Department of Transportation Program Manager, Cities for Cycling NACTO President Carl Sundstrom, P.E. New York City Department of Matthew Roe Robin Hutcheson Transportation Technical Lead Director of Public Works, City of Aaron Villere Minneapolis Peter Koonce, P.E. Senior Program Associate NACTO Vice President Portland Bureau of Transportation, Portland, OR Celine Schmidt Robert Spillar Design Associate Director of Transportation, City Mike Sallaberry, P.E. San Francisco Municipal of Austin Majed Abdulsamad Transportation Agency NACTO Treasurer Program Associate Michael Carroll Peter Bennett Deputy Managing Director, San José Department of Office of Transportation and Transportation, CA Technical Review Infrastructure Systems, City of Dylan Passmore, P.Eng. Philadelphia Joe Gilpin City of Vancouver, BC NACTO Secretary Alta Planning & Design David Rawsthorne, P.Eng. Joseph E. Barr Vignesh Swaminathan, P.E. City of Vancouver, BC Director, Traffic, Parking Crossroad Lab & Transportation, City of Dongho Chang, P.E. Cambridge Seattle Department of NACTO Affiliate Member Transportation Acknowledgments Representative This document was funded by a grant from the The John S. and James L. Advisory Committee Knight Foundation. NACTO Cities for Cycling Special thanks to Robert Boler from Committee representatives Austin, TX for providing the inspiration for the title of this document.
    [Show full text]
  • Sets and Venn Diagrams
    The Improving Mathematics Education in Schools (TIMES) Project NUMBER AND ALGEBRA Module 1 SETS AND VENN DIAGRAMS A guide for teachers - Years 7–8 June 2011 YEARS 78 Sets and Venn diagrams (Number and Algebra : Module 1) For teachers of Primary and Secondary Mathematics 510 Cover design, Layout design and Typesetting by Claire Ho The Improving Mathematics Education in Schools (TIMES) Project 2009‑2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations. The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations. © The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE‑EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution‑ NonCommercial‑NoDerivs 3.0 Unported License. 2011. http://creativecommons.org/licenses/by‑nc‑nd/3.0/ The Improving Mathematics Education in Schools (TIMES) Project NUMBER AND ALGEBRA Module 1 SETS AND VENN DIAGRAMS A guide for teachers - Years 7–8 June 2011 Peter Brown Michael Evans David Hunt Janine McIntosh Bill Pender Jacqui Ramagge YEARS 78 {1} A guide for teachers SETS AND VENN DIAGRAMS ASSUMED KNOWLEDGE • Addition and subtraction of whole numbers. • Familiarity with the English words ‘and’, ‘or’, ‘not’, ‘all’, ‘if…then’. MOTIVATION In all sorts of situations we classify objects into sets of similar objects and count them. This procedure is the most basic motivation for learning the whole numbers and learning how to add and subtract them.
    [Show full text]