DOCSLIB.ORG

Glossary of CAD Terms

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Glossary of CAD Terms AutoCAD and Its Applications BASICS Reference Material Glossary of CAD Terms 1D unit block: A 1-unit, one-dimensional aligned dimensioning: A dimensioning object, such as a straight line segment, system in which dimension values align saved as a block. with dimension lines. 2D unit block: A 2D object that fits into a aligned section: Section used when 1-unit × 1-unit square, saved as a block. a feature is out of alignment with the center plane. 3D unit block: A 3D object that fits into a 1-unit × 1-unit × 1-unit cube, saved as a alignment parameter: A parameter that block. aligns a block with another object in the drawing. alignment paths: Temporary lines and A arcs that coincide with the position of existing objects. absolute coordinates: Coordinate alternate units (dual dimensioning distances measured from the origin. units): Dimensions in which measurements in one system, such absolute path: A path to a file defined by as inches, are followed by bracketed the location of the file on the computer measurements in another system, such as system. millimeters. absolute value: In property settings, a angular dimensioning: A method of value set directly instead of referenced by a dimensioning angles in which one corner layer or a block. An absolute value ignores of an angle is located with a dimension the current layer settings. and the value of the angle is provided in acquired point: A point found by moving degrees. the crosshairs over a point on an existing annotation: Textual information presented object to reference the point when picking in notes, specifications, comments, and a new point. symbols. action: A definition that controls how annotational format: A dimensional dynamic block parameters behave. constraint format in which the constraints action bars: Toolbars that allow you to look like traditional dimensions, using a view, remove, and adjust actions. dimension style. Annotational dimensional constraints can still control the size or action parameter (parameter): A location of geometry. specification for block construction that controls block characteristics such as annotation scale: The scale AutoCAD positions, distances, and angles of dynamic uses to calculate the scale factor applied to block geometry. annotative objects. alert: A pop-up that indicates a required annotative object representation: Display action or potential problem. of an annotative object at an annotation scale that the object supports. Copyright Goodheart-Willcox Co., Inc. Glossary of CAD Terms 1 May not be reproduced or posted to a publicly accessible website. annotative objects: AutoCAD objects that B can adapt automatically to the current drawing scale. annotative text: Text scaled by AutoCAD background mask: A mask that hides a according to the specified annotation scale. portion of objects behind and around text so that the text is unobstructed. arc: Any portion of a circle, usually dimensioned according to the radius (R). balloons: Circles that contain a number or letter to identify the assembly component archiving: Gathering and storing all and correlate the component to a parts list drawings and associated files related to a or bill of materials. Balloons connect to a project. component with a leader line. array: Multiple copies of an object base dimension: The dimension line that arranged in a pattern. remains in the same location, with which array action: An action used to array other dimension lines align or space. objects within the block based on preset baseline dimensioning: A method of specifications. dimensioning in which several dimensions associated list: The ASME term describing originate from a common surface, tables added or related to engineering centerline, or center plane. drawings. base point: The initial reference point associative array: An adjustable array AutoCAD uses when stretching, moving, object; all items are grouped to form copying, and scaling objects. a single object, allowing you to make base point parameter: A parameter that modifications such as changing the number defines an alternate base point for a block. of items and spacing between items. basic dimension: A theoretically perfect associative dimension: A dimension dimension used to describe the exact associated with an object. The dimension size, profile, orientation, and location of a value updates automatically when the feature. object changes. big font: A supplement that provides associative hatch pattern: A hatch pattern Asian and other large-format fonts that that updates automatically when you edit have characters and symbols not present in associated objects. other font files. attachment: An xref linked with or bilateral tolerance: A tolerance style that referenced into the current drawing. permits variance in both the positive and attributes: Text-based data assigned to a negative directions from the specified specific object. Attributes turn a drawing dimension. into a graphical database. bind: Convert an xref to a permanently auto-fill: A table function that fills selected inserted block in the host drawing. cells based on the contents of another cell. block: An object, such as a symbol, saved automatic save: A save procedure that and stored in a drawing for future use. occurs at specified intervals without block definition: Information about a your input. block stored within the drawing file. automatic windowing (implied block insertion tools: Blocks located on a windowing): A selection method that tool palette. allows you to select multiple objects at one time without entering a selection option. block properties table: A table of action parameters and/or constraint parameters auxiliary view: View used to show the that allows you to create multiple block true size and shape of a foreshortened properties and then select them to create surface. block references. Copyright Goodheart-Willcox Co., Inc. Glossary of CAD Terms 2 May not be reproduced or posted to a publicly accessible website. block reference: A specific instance of a check box: A selectable box that turns block inserted into a drawing. an item on (when checked) or off (when unchecked). boundary: The area filled by a hatch. child: A style override. boundary edge: The edge to which objects such as lines, arcs, and polylines extend. chord length: The linear distance between two points on a circle or arc. boundary set: The part of the drawing AutoCAD evaluates to define a boundary. circle: A closed curve with a constant radius (R) around a center point; broken-out section: Section that shows a usually dimensioned according to the small portion of the object removed. diameter (∅). BSI: British Standards Institution. circular reference error: An error that button: A “hot spot” button on the screen occurs when a block definition references that you pick to access an application, itself. command, or option. circumscribed polygon: A polygon drawn outside an imaginary circle so that the sides of the polygon are tangent to the C circle. coincident: A geometric construction that callout block: A block that uses attributes specifies two points sharing the same containing fields that link the view position. number and sheet title between the sheet color-dependent plot style table: A file set and drawing (sheet) views. that contains plot style settings used to Cartesian (rectangular) coordinate assign plot values to object colors. system: A system that locates points in command: An instruction issued to the space according to distances from three computer to complete a specific task. For intersecting axes. example, use the LINE command to draw cascading menu (cascading submenu): line objects. A menu of options related to the chosen command alias: Abbreviated command menu item. name entered at the keyboard. cell styles: Styles that allow you to assign command line: Area where you can type specific formatting to data, header, and commands (command names) and type or title row cells. select command options. centroid: The mathematical center of a Commercial and Government Entity geometric figure. Code (CAGE Code): A five-digit chain action: An action that triggers numerical code identifier applicable to any another action when you modify a organization that produces items used by parameter. the federal government. chain dimensioning: A method of composition: The spacing, layout, and dimensioning in which dimensions appear appearance of text. in a line from one feature to the next. computer-aided design and drafting chamfer: In mechanical drafting, a small, (CADD): The process of using a computer angled surface used to relieve a sharp corner. with CADD software to design and produce drawings and models. chart dimensioning: A type of dimensioning in which the variable concentric: Describes arcs, circles, and/or dimensions are shown with letters that ellipses sharing the same center point. correlate to a chart in which the possible configured: Installed and ready to use. dimensions are given. Copyright Goodheart-Willcox Co., Inc. Glossary of CAD Terms 3 May not be reproduced or posted to a publicly accessible website. constant: An expression or value that stays current layer: The active layer. Whatever the same. you draw is placed on the current layer. constraint parameters: Dimensional curve fitting: Converting a polyline into a constraints available for block construction series of smooth curves. to control the size or location of block cutting edge: An object such as a line, geometry numerically. arc, or text that defines the point (edge) at construction lines: Lines commonly used which the object you trim will be cut. to lay out a drawing. cutting-plane line: The line that cuts context-oriented help: Help information through the object to expose internal for the active command. features. context-sensitive: Specific to the active cycle: Repeatedly select a series of command or option. stacked objects until the desired object is highlighted. continued dimensioning: The AutoCAD term for chain dimensioning. control code sequence: A key sequence D beginning with %% that defines symbols in text. control vertices: Points that are used to datum: Theoretically perfect surface, define the curve shape and change the curve plane, point, or axis from which design.
Load more

Recommended publications
  • Glossary Physics (I-Introduction)
    1 Glossary Physics (I-introduction) - Efficiency: The percent of the work put into a machine that is converted into useful work output; = work done / energy used [-]. = eta In machines: The work output of any machine cannot exceed the work input (<=100%); in an ideal machine, where no energy is transformed into heat: work(input) = work(output), =100%. Energy: The property of a system that enables it to do work. Conservation o. E.: Energy cannot be created or destroyed; it may be transformed from one form into another, but the total amount of energy never changes. Equilibrium: The state of an object when not acted upon by a net force or net torque; an object in equilibrium may be at rest or moving at uniform velocity - not accelerating. Mechanical E.: The state of an object or system of objects for which any impressed forces cancels to zero and no acceleration occurs. Dynamic E.: Object is moving without experiencing acceleration. Static E.: Object is at rest.F Force: The influence that can cause an object to be accelerated or retarded; is always in the direction of the net force, hence a vector quantity; the four elementary forces are: Electromagnetic F.: Is an attraction or repulsion G, gravit. const.6.672E-11[Nm2/kg2] between electric charges: d, distance [m] 2 2 2 2 F = 1/(40) (q1q2/d ) [(CC/m )(Nm /C )] = [N] m,M, mass [kg] Gravitational F.: Is a mutual attraction between all masses: q, charge [As] [C] 2 2 2 2 F = GmM/d [Nm /kg kg 1/m ] = [N] 0, dielectric constant Strong F.: (nuclear force) Acts within the nuclei of atoms: 8.854E-12 [C2/Nm2] [F/m] 2 2 2 2 2 F = 1/(40) (e /d ) [(CC/m )(Nm /C )] = [N] , 3.14 [-] Weak F.: Manifests itself in special reactions among elementary e, 1.60210 E-19 [As] [C] particles, such as the reaction that occur in radioactive decay.
    [Show full text]
  • Center of Mass and Centroids
    Center of Mass and Centroids Center of Mass A body of mass m in equilibrium under the action of tension in the cord, and resultant W of the gravitational forces acting on all particles of the body. -The resultant is collinear with the cord Suspend the body at different points -Dotted lines show lines of action of the resultant force in each case. -These lines of action will be concurrent at a single point G As long as dimensions of the body are smaller compared with those of the earth. - we assume uniform and parallel force field due to the gravitational attraction of the earth. The unique Point G is called the Center of Gravity of the body (CG) ME101 - Division III Kaustubh Dasgupta 1 Center of Mass and Centroids Determination of CG - Apply Principle of Moments Moment of resultant gravitational force W about any axis equals sum of the moments about the same axis of the gravitational forces dW acting on all particles treated as infinitesimal elements. Weight of the body W = ∫dW Moment of weight of an element (dW) @ x-axis = ydW Sum of moments for all elements of body = ∫ydW From Principle of Moments: ∫ydW = ӯ W Moment of dW @ z axis??? xdW ydW zdW x y z = 0 or, 0 W W W Numerator of these expressions represents the sum of the moments; Product of W and corresponding coordinate of G represents the moment of the sum Moment Principle. ME101 - Division III Kaustubh Dasgupta 2 Center of Mass and Centroids xdW ydW zdW x y z Determination of CG W W W Substituting W = mg and dW = gdm xdm ydm zdm x y z m m m In vector notations:
    [Show full text]
  • Dynamics of Urban Centre and Concepts of Symmetry: Centroid and Weighted Mean
    Jong-Jin Park Research École Polytechnique Fédérale de Dynamics of Urban Centre and Lausanne (EPFL) Laboratoire de projet urbain, Concepts of Symmetry: territorial et architectural (UTA) Centroid and Weighted Mean BP 4137, Station 16 CH-1015 Lausanne Presented at Nexus 2010: Relationships Between Architecture SWITZERLAND and Mathematics, Porto, 13-15 June 2010. [email protected] Abstract. The city is a kind of complex system being capable Keywords: evolving structure, of auto-organization of its programs and adapts a principle of urban system, programmatic economy in its form generating process. A new concept of moving centre, centroid, dynamic centre in urban system, called “the programmatic weighted mean, symmetric moving centre”, can be used to represent the successive optimization, successive appearances of various programs based on collective facilities equilibrium and their potential values. The absolute central point is substituted by a magnetic field composed of several interactions among the collective facilities and also by the changing value of programs through time. The center moves continually into this interactive field. Consequently, we introduce mathematical methods of analysis such as “the centroid” and “the weighted mean” to calculate and visualize the dynamics of the urban centre. These methods heavily depend upon symmetry. We will describe and establish the moving centre from a point of view of symmetric optimization that answers the question of the evolution and successive equilibrium of the city. In order to explain and represent dynamic transformations in urban area, we tested this programmatic moving center in unstable and new urban environments such as agglomeration areas around Lausanne in Switzerland.
    [Show full text]
  • Forces Different Types of Forces
    Forces and motion are a part of your everyday life for example pushing a trolley, a horse pulling a rope, speed and acceleration. Force and motion causes objects to move but also to stay still. Motion is simply a movement but needs a force to move. There are 2 types of forces, contact forces and act at a distance force. Forces Every day you are using forces. Force is basically push and pull. When you push and pull you are applying a force to an object. If you are Appling force to an object you are changing the objects motion. For an example when a ball is coming your way and then you push it away. The motion of the ball is changed because you applied a force. Different Types of Forces There are more forces than push or pull. Scientists group all these forces into two groups. The first group is contact forces, contact forces are forces when 2 objects are physically interacting with each other by touching. The second group is act at a distance force, act at a distance force is when 2 objects that are interacting with each other but not physically touching. Contact Forces There are different types of contact forces like normal Force, spring force, applied force and tension force. Normal force is when nothing is happening like a book lying on a table because gravity is pulling it down. Another contact force is spring force, spring force is created by a compressed or stretched spring that could push or pull. Applied force is when someone is applying a force to an object, for example a horse pulling a rope or a boy throwing a snow ball.
    [Show full text]
  • Chapter 5 –3 Center and Centroids
    ENGR 0135 Chapter 5 –3 Center and centroids Department of Mechanical Engineering Centers and Centroids Center of gravity Center of mass Centroid of volume Centroid of area Centroid of line Department of Mechanical Engineering Center of Gravity A point where all of the weight could be concentrated without changing the external effects of the body To determine the location of the center, we may consider the weight system as a 3D parallel force system Department of Mechanical Engineering Center of Gravity – discrete bodies The total weight isWW i The location of the center can be found using the total moments 1 M Wx W x xW x yz G i i G W i i 1 M Wy W y yW y zx G i i G W i i 1 M Wz W z z W z xy G i i G W i i Department of Mechanical Engineering Center of Gravity – continuous bodies The total weight Wis dW The location of the center can be found using the total moments 1 M Wx xdW x xdW yz G G W 1 M Wy ydW y ydW zx G G W 1 M Wz zdW z zdW xy G G W Department of Mechanical Engineering Center of Mass A point where all of the mass could be concentrated It is the same as the center of gravity when the body is assumed to have uniform gravitational force Mass of particles 1 n 1 n 1 n n xC xi m i C y yi m i C z z mi i m i m m i m i m i i Continuous mass 1 1 1 x x dm yy dmz z dm m dm G m G m G m Department of Mechanical Engineering Example:Example: CenterCenter ofof discretediscrete massmass List the masses and the coordinates of their centroids in a table Compute the first moment of each mass (relative
    [Show full text]
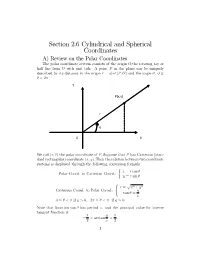
  • Section 2.6 Cylindrical and Spherical Coordinates
    Section 2.6 Cylindrical and Spherical Coordinates A) Review on the Polar Coordinates The polar coordinate system consists of the origin O,the rotating ray or half line from O with unit tick. A point P in the plane can be uniquely described by its distance to the origin r = dist (P, O) and the angle µ, 0 µ < 2¼ : · Y P(x,y) r θ O X We call (r, µ) the polar coordinate of P. Suppose that P has Cartesian (stan- dard rectangular) coordinate (x, y) .Then the relation between two coordinate systems is displayed through the following conversion formula: x = r cos µ Polar Coord. to Cartesian Coord.: y = r sin µ ½ r = x2 + y2 Cartesian Coord. to Polar Coord.: y tan µ = ( p x 0 µ < ¼ if y > 0, 2¼ µ < ¼ if y 0. · · · Note that function tan µ has period ¼, and the principal value for inverse tangent function is ¼ y ¼ < arctan < . ¡ 2 x 2 1 So the angle should be determined by y arctan , if x > 0 xy 8 arctan + ¼, if x < 0 µ = > ¼ x > > , if x = 0, y > 0 < 2 ¼ , if x = 0, y < 0 > ¡ 2 > > Example 6.1. Fin:>d (a) Cartesian Coord. of P whose Polar Coord. is ¼ 2, , and (b) Polar Coord. of Q whose Cartesian Coord. is ( 1, 1) . 3 ¡ ¡ ³ So´l. (a) ¼ x = 2 cos = 1, 3 ¼ y = 2 sin = p3. 3 (b) r = p1 + 1 = p2 1 ¼ ¼ 5¼ tan µ = ¡ = 1 = µ = or µ = + ¼ = . 1 ) 4 4 4 ¡ 5¼ Since ( 1, 1) is in the third quadrant, we choose µ = so ¡ ¡ 4 5¼ p2, is Polar Coord.
    [Show full text]
  • Geodesic Distance Descriptors
    Geodesic Distance Descriptors Gil Shamai and Ron Kimmel Technion - Israel Institute of Technologies [email protected] [email protected] Abstract efficiency of state of the art shape matching procedures. The Gromov-Hausdorff (GH) distance is traditionally used for measuring distances between metric spaces. It 1. Introduction was adapted for non-rigid shape comparison and match- One line of thought in shape analysis considers an ob- ing of isometric surfaces, and is defined as the minimal ject as a metric space, and object matching, classification, distortion of embedding one surface into the other, while and comparison as the operation of measuring the discrep- the optimal correspondence can be described as the map ancies and similarities between such metric spaces, see, for that minimizes this distortion. Solving such a minimiza- example, [13, 33, 27, 23, 8, 3, 24]. tion is a hard combinatorial problem that requires pre- Although theoretically appealing, the computation of computation and storing of all pairwise geodesic distances distances between metric spaces poses complexity chal- for the matched surfaces. A popular way for compact repre- lenges as far as direct computation and memory require- sentation of functions on surfaces is by projecting them into ments are involved. As a remedy, alternative representa- the leading eigenfunctions of the Laplace-Beltrami Opera- tion spaces were proposed [26, 22, 15, 10, 31, 30, 19, 20]. tor (LBO). When truncated, the basis of the LBO is known The question of which representation to use in order to best to be the optimal for representing functions with bounded represent the metric space that define each form we deal gradient in a min-max sense.
    [Show full text]
  • Designing Patterns with Polar Equations Using Maple
    Designing Patterns with Polar Equations using Maple Somasundaram Velummylum Claflin University Department of Mathematics and Computer Science 400 Magnolia St Orangeburg, South Carolina 29115 U.S.A [email protected] The Cartesian coordinates and polar coordinates can be used to identify a point in two dimensions. The polar coordinate system has a fixed point O called the origin or pole and a directed half –line called the polar axis with end point O. A point P on the plane can be described by the polar coordinates ( r, θ ), where r is the radial distance from the origin and θ is the angle made by OP with the polar axis. Several important types of graphs have equations that are simpler in polar form than in rectangular form. For example, the polar equation of a circle having radius a and centered at the origin is simply r = a. In other words , polar coordinate system is useful in describing two dimensional regions that may be difficult to describe using Cartesian coordinates. For example, graphing the circle x 2 + y 2 = a 2 in Cartesian coordinates requires two functions, one for the upper half and one for the lower half. In polar coordinate system, the same circle has the very simple representation r = a. Maple can be used to create patterns in two dimensions using polar coordinate system. When we try to analyze two dimensional patterns mathematically it will be helpful if we can draw a set of patterns in different colors using the help of technology. To investigate and compare some patterns we will go through some examples of cardioids and rose curves that are drawn using Maple.
    [Show full text]
  • Robust Topological Inference: Distance to a Measure and Kernel Distance
    Journal of Machine Learning Research 18 (2018) 1-40 Submitted 9/15; Revised 2/17; Published 4/18 Robust Topological Inference: Distance To a Measure and Kernel Distance Fr´ed´ericChazal [email protected] Inria Saclay - Ile-de-France Alan Turing Bldg, Office 2043 1 rue Honor´ed'Estienne d'Orves 91120 Palaiseau, FRANCE Brittany Fasy [email protected] Computer Science Department Montana State University 357 EPS Building Montana State University Bozeman, MT 59717 Fabrizio Lecci [email protected] New York, NY Bertrand Michel [email protected] Ecole Centrale de Nantes Laboratoire de math´ematiquesJean Leray 1 Rue de La Noe 44300 Nantes FRANCE Alessandro Rinaldo [email protected] Department of Statistics Carnegie Mellon University Pittsburgh, PA 15213 Larry Wasserman [email protected] Department of Statistics Carnegie Mellon University Pittsburgh, PA 15213 Editor: Mikhail Belkin Abstract Let P be a distribution with support S. The salient features of S can be quantified with persistent homology, which summarizes topological features of the sublevel sets of the dis- tance function (the distance of any point x to S). Given a sample from P we can infer the persistent homology using an empirical version of the distance function. However, the empirical distance function is highly non-robust to noise and outliers. Even one outlier is deadly. The distance-to-a-measure (DTM), introduced by Chazal et al. (2011), and the ker- nel distance, introduced by Phillips et al. (2014), are smooth functions that provide useful topological information but are robust to noise and outliers. Chazal et al. (2015) derived concentration bounds for DTM.
    [Show full text]
  • Centroids by Composite Areas.Pptx
    Centroids Method of Composite Areas A small boy swallowed some coins and was taken to a hospital. When his grandmother telephoned to ask how he was a nurse said 'No change yet'. Centroids ¢ Previously, we developed a general formulation for finding the centroid for a series of n areas n xA ∑ ii i=1 x = n A ∑ i i=1 2 Centroids by Composite Areas Monday, November 12, 2012 1 Centroids ¢ xi was the distance from the y-axis to the local centroid of the area Ai n xA ∑ ii i=1 x = n A ∑ i i=1 3 Centroids by Composite Areas Monday, November 12, 2012 Centroids ¢ If we can break up a shape into a series of smaller shapes that have predefined local centroid locations, we can use this formula to locate the centroid of the composite shape n xA ∑ ii i=1 x = n A ∑ i 4 Centroids by Composite Areas i=1 Monday, November 12, 2012 2 Centroid by Composite Bodies ¢ There is a table in the back cover of your book that gives you the location of local centroids for a select group of shapes ¢ The point labeled C is the location of the centroid of that shape. 5 Centroids by Composite Areas Monday, November 12, 2012 Centroid by Composite Bodies ¢ Please note that these are local centroids, they are given in reference to the x and y axes as shown in the table. 6 Centroids by Composite Areas Monday, November 12, 2012 3 Centroid by Composite Bodies ¢ For example, the centroid location of the semicircular area has the y-axis through the center of the area and the x-axis at the bottom of the area ¢ The x-centroid would be located at 0 and the y-centroid would be located
    [Show full text]
  • Position Management System Online Subject Area
    USDA, NATIONAL FINANCE CENTER INSIGHT ENTERPRISE REPORTING Business Intelligence Delivered Insight Quick Reference | Position Management System Online Subject Area What is Position Management System Online (PMSO)? • This Subject Area provides snapshots in time of organization position listings including active (filled and vacant), inactive, and deleted positions. • Position data includes a Master Record, containing basic position data such as grade, pay plan, or occupational series code. • The Master Record is linked to one or more Individual Positions containing organizational structure code, duty station code, and accounting station code data. History • The most recent daily snapshot is available during a given pay period until BEAR runs. • Bi-Weekly snapshots date back to Pay Period 1 of 2014. Data Refresh* Position Management System Online Common Reports Daily • Provides daily results of individual position information, HR Area Report Name Load which changes on a daily basis. Bi-Weekly Organization • Position Daily for current pay and Position Organization with period/ Bi-Weekly • Provides the latest record regardless of previous changes Management PII (PMSO) for historical pay that occur to the data during a given pay period. periods *View the Insight Data Refresh Report to determine the most recent date of refresh Reminder: In all PMSO reports, users should make sure to include: • An Organization filter • PMSO Key elements from the Master Record folder • SSNO element from the Incumbent Employee folder • A time filter from the Snapshot Time folder 1 USDA, NATIONAL FINANCE CENTER INSIGHT ENTERPRISE REPORTING Business Intelligence Delivered Daily Calendar Filters Bi-Weekly Calendar Filters There are three time options when running a bi-weekly There are two ways to pull the most recent daily data in a PMSO report: PMSO report: 1.
    [Show full text]
  • Chapters, in This Chapter We Present Methods Thatare Not Yet Employed by Industrial Robots, Except in an Extremely Simplifiedway
    C H A P T E R 11 Force control of manipulators 11.1 INTRODUCTION 11.2 APPLICATION OF INDUSTRIAL ROBOTS TO ASSEMBLY TASKS 11.3 A FRAMEWORK FOR CONTROL IN PARTIALLY CONSTRAINED TASKS 11.4 THE HYBRID POSITION/FORCE CONTROL PROBLEM 11.5 FORCE CONTROL OFA MASS—SPRING SYSTEM 11.6 THE HYBRID POSITION/FORCE CONTROL SCHEME 11.7 CURRENT INDUSTRIAL-ROBOT CONTROL SCHEMES 11.1 INTRODUCTION Positioncontrol is appropriate when a manipulator is followinga trajectory through space, but when any contact is made between the end-effector and the manipulator's environment, mere position control might not suffice. Considera manipulator washing a window with a sponge. The compliance of thesponge might make it possible to regulate the force applied to the window by controlling the position of the end-effector relative to the glass. If the sponge isvery compliant or the position of the glass is known very accurately, this technique could work quite well. If, however, the stiffness of the end-effector, tool, or environment is high, it becomes increasingly difficult to perform operations in which the manipulator presses against a surface. Instead of washing with a sponge, imagine that the manipulator is scraping paint off a glass surface, usinga rigid scraping tool. If there is any uncertainty in the position of the glass surfaceor any error in the position of the manipulator, this task would become impossible. Either the glass would be broken, or the manipulator would wave the scraping toolover the glass with no contact taking place. In both the washing and scraping tasks, it would bemore reasonable not to specify the position of the plane of the glass, but rather to specifya force that is to be maintained normal to the surface.
    [Show full text]