Quadrature Amplitude Modulation Division for Multiuser MISO Broadcast Channels Zheng Dong, Yan-Yu Zhang, Jian-Kang Zhang, Senior Member, IEEE and Xiang-Chuan Gao
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Most Common Digital Modulation Techniques Are: Phase-Shift Keying
Common Digital Modulation Techniques and Pulse Modulation Methods The most common digital modulation techniques are: Phase-shift keying (PSK): o Binary PSK (BPSK), using M=2 symbols o Quadrature PSK (QPSK), using M=4 symbols o 8PSK, using M=8 symbols o 16PSK, using M=16 symbols o Differential PSK (DPSK) o Differential QPSK (DQPSK) o Offset QPSK (OQPSK) o π/4–QPSK Frequency-shift keying (FSK): o Audio frequency-shift keying (AFSK) o Multi-frequency shift keying (M-ary FSK or MFSK) o Dual-tone multi-frequency (DTMF) o Continuous-phase frequency-shift keying (CPFSK) Amplitude-shift keying (ASK) On-off keying (OOK), the most common ASK form o M-ary vestigial sideband modulation, for example 8VSB Quadrature amplitude modulation (QAM) - a combination of PSK and ASK: o Polar modulation like QAM a combination of PSK and ASK.[citation needed] Continuous phase modulation (CPM) methods: o Minimum-shift keying (MSK) o Gaussian minimum-shift keying (GMSK) Orthogonal frequency-division multiplexing (OFDM) modulation: o discrete multitone (DMT) - including adaptive modulation and bit-loading. Wavelet modulation Trellis coded modulation (TCM), also known as trellis modulation Spread-spectrum techniques: o Direct-sequence spread spectrum (DSSS) o Chirp spread spectrum (CSS) according to IEEE 802.15.4a CSS uses pseudo-stochastic coding o Frequency-hopping spread spectrum (FHSS) applies a special scheme for channel release MSK and GMSK are particular cases of continuous phase modulation. Indeed, MSK is a particular case of the sub-family of CPM known as continuous-phase frequency-shift keying (CPFSK) which is defined by a rectangular frequency pulse (i.e. -

Software Defined Acoustic Underwater Modem
Software Defined Acoustic Underwater Modem Jakob Lindgren April 13, 2011 Abstract Today many types of communication are employed on seagoing vessels, such as radio, satellite and Wi-Fi but only one type of communication is practical for submerged vessels, the acoustic underwater modem. The ”off-the-shelf” modems are sometimes difficult to update and replace, especially on a large submarine. But by separating the hardware from the signal processing and making the software modular more versatility can be achieved. The questions that this thesis are asking are: is it possible to implement the signal processing in software? How small or large should the modules be? What kind of architecture should be used? This thesis shows that it is indeed possible to implement simple algorithms that can isolate a signal and read its content regardless of the hardware configuration. Calculations show that up to 13 kbps can be reached at a range of one kilometer. It is most practical to make the entire physical layer into one module and the size of the system could drastically change the type of architecture used. 1 Preface This Master's thesis from Jakob Lindgren is the final project for receiving the Master's degree in Robotics at M¨alardalenUniversity in V¨aster˚as,Sweden. It covers the basics of digital communication in the underwater channel as well as some simple algorithms for software defined communication. The purpose of this master thesis is to investigate how a software defined acoustic underwater communication can be implemented. This work was done at Saab Underwater Systems in Motala, Sweden, during the autumn term of 2010. -

Etsi En 302 878-2 V1.1.1 (2011-11)
ETSI EN 302 878-2 V1.1.1 (2011-11) European Standard Access, Terminals, Transmission and Multiplexing (ATTM); Third Generation Transmission Systems for Interactive Cable Television Services - IP Cable Modems; Part 2: Physical Layer; DOCSIS 3.0 2 ETSI EN 302 878-2 V1.1.1 (2011-11) Reference DEN/ATTM-003006-2 Keywords access, broadband, cable, data, IP, IPCable, modem ETSI 650 Route des Lucioles F-06921 Sophia Antipolis Cedex - FRANCE Tel.: +33 4 92 94 42 00 Fax: +33 4 93 65 47 16 Siret N° 348 623 562 00017 - NAF 742 C Association à but non lucratif enregistrée à la Sous-Préfecture de Grasse (06) N° 7803/88 Important notice Individual copies of the present document can be downloaded from: http://www.etsi.org The present document may be made available in more than one electronic version or in print. In any case of existing or perceived difference in contents between such versions, the reference version is the Portable Document Format (PDF). In case of dispute, the reference shall be the printing on ETSI printers of the PDF version kept on a specific network drive within ETSI Secretariat. Users of the present document should be aware that the document may be subject to revision or change of status. Information on the current status of this and other ETSI documents is available at http://portal.etsi.org/tb/status/status.asp If you find errors in the present document, please send your comment to one of the following services: http://portal.etsi.org/chaircor/ETSI_support.asp Copyright Notification No part may be reproduced except as authorized by written permission. -

Download Article
IJIRST –International Journal for Innovative Research in Science & Technology| Volume 1 | Issue 8 | January 2015 ISSN (online): 2349-6010 High Speed Low Power Veterbi Decoder For TCM Decoders Using Xilinx T.Mahesh Kumar P.Vijai Bhaskar M.Tech (VLSI) Head of the Department Department of Electronics & Communication Engineering, Department of Electronics & Communication Engineering, JNTUH JNTUH AVN Institute of Engineering & Technology Telangana, India AVN Institute of Engineering & Technology Telangana, India Abstract It is well known that the Viterbi decoder (VD) is the dominant module determining the overall power consumption of TCM decoders. High-speed, low-power design of Viterbi decoders for trellis coded modulation (TCM) systems is presented in this paper. We propose a pre-computation architecture incorporated with -algorithm for VD, which can effectively reduce the power consumption without degrading the decoding speed much. A general solution to derive the optimal pre-computation steps is also given in the paper. Implementation result of a VD for a rate-3/4 convolutional code used in a TCM system shows that compared with the full trellis VD, the precomputation architecture reduces the power consumption by as much as 70% without performance loss, while the degradation in clock speed is negligible. Keywords: Viterbi Decoder, VLSI, Trellis Coded Modulation (TCM). _______________________________________________________________________________________________________ I. INTRODUCTION In telecommunication, trellis modulation (also known as trellis coded modulation, or simply TCM) is a modulation scheme which allows highly efficient transmission of information over band-limited channels such as telephone lines. Trellis modulation was invented by Gottfried Ungerboeck working for IBM in the 1970s, and first described in a conference paper in 1976; but it went largely unnoticed until he published a new detailed exposition in 1982 which achieved sudden widespread recognition. -

Performance Analysis of MIMO Spatial Multiplexing Using Different Antenna Configurations and Modulation Technique in Rician Channel Hardeep Singh, Lavish Kansal
International Journal of Scientific & Engineering Research, Volume 5, Issue 6, June-2014 34 ISSN 2229-5518 Performance Analysis of MIMO Spatial Multiplexing using different Antenna Configurations and Modulation Technique in Rician Channel Hardeep Singh, Lavish Kansal Abstract— MIMO systems which employs multiple antennas at the transmitter as well as at the receiver side is the key technique to be employed in next generation wireless communication systems. MIMO systems provide various benefits such as Spatial Diversity, Spatial Multiplexing to improve the system performance. In this paper the MIMO SM system is analysed for different antenna configurations (2×2, 3×3, 4×4) in Rician channel. The performance of the MIMO SM system is investigated for higher order modulation schemes (M-PSK, M-QAM) and Zero Forcing equalizer is employed at the receiving side. The simulation results points that if antenna configurations are shifted from 2×2 to 3×3 configuration, an improvement of 0 to 2.9 db in SNR is being noted and an improvement of 0 to 2.9 db is visualized if antenna configurations are changed from 3×3 to 4×4 configuration. Index Terms— Multiple Input Multiple Output (MIMO), Zero Forcing (ZF), Spatial Multiplexing (SM), M-ary Phase Shift Keying (M-PSK) M-ary Quadrature Amplitude Modulation (M-QAM), Bit Error Rate (BER), Signal to Noise Ratio (SNR). —————————— —————————— 1 INTRODUCTION IMO (Multiple Input Multiple Output) systems employ higher extend, but the benefits of beamforming technique are multiple antennas at both the ends of a communication limited in such environments. Mlink. The MIMO systems provide various applications In order to obtain channel state information at receiving side, such as beamforming (increasing the average SNR at receiver the pilot bits are sent along with the transmitted sequence to side), Spatial Diversity (to achieve good BER at low SNR), Spa- estimate the channel state. -
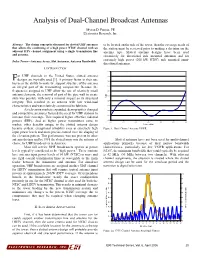
Analysis of Dual-Channel Broadcast Antennas
Analysis of Dual-Channel Broadcast Antennas Myron D. Fanton, PE Electronics Research, Inc. Abstract—The design concept is discussed for slotted UHF antennas to be located on the side of the tower, then the coverage needs of that allows the combining of a high power NTSC channel with an the station must be reviewed prior to making a decision on the adjacent DTV channel assignment using a single transmission line antenna type. Slotted antenna designs have been used and antenna. extensively for directional side mounted antennas and for extremely high power (200 kW NTSC) side mounted omni- Index Terms—Antenna Array, Slot Antennas, Antenna Bandwidth. directional antennas. I. INTRODUCTION 1.10 or UHF channels in the United States, slotted antenna 1.09 designs are typically used [1]. A primary factor in their use F 1.08 has been the ability to make the support structure of the antenna an integral part of the transmitting components. Because the 1.07 frequencies assigned to UHF allow the use of relatively small 1.06 antenna elements, the removal of part of the pipe wall to create 1.05 slots was possible with only a minimal impact an its structural VSWR integrity. This resulted in an antenna with low wind-load 1.04 characteristics and was relatively economical to fabricate. 1.03 As television markets expanded, demographics changed 1.02 and competitive pressures fostered the need for UHF stations to increase their coverage. This required higher effective radiated 1.01 1.00 powers (ERP). And as higher power transmitters came to 572 574 576 578 580 582 584 market, other benefits unique to the slotted antenna design Frequency (MHz) became evident: exceptional reliability even at extremely high Figure 1: Dual Channel Antenna VSWR input power levels and more precise control over the shaping of the elevation pattern. -

Importance of Microwave Antenna in Communication System
ISSN (Print) : 2320 – 3765 ISSN (Online): 2278 – 8875 International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering (A High Impact Factor, Monthly, Peer Reviewed Journal) Website: www.ijareeie.com Vol. 7, Issue 2, February 2018 Importance of Microwave Antenna in Communication System Shailesh Patwa1, Shubham Yadav2, Mohammad Saqib3 UG Student [BE], Dept. of ECE, Medicaps Institute of Technology and Management College, Indore, Madhya Pradesh, India1 UG Student [BE], Dept. of ECE, Medicaps Institute of Technology and Management College, Indore, Madhya Pradesh, India2 UG Student [BE], Dept. of ECE, Medicaps Institute of Technology and Management College, Indore, Madhya Pradesh, India3 ABSTRACT: This paper provide various types of information about microwave antenna in communication system. Antenna plays a crucial role in this communication system, which is used to transmit and receive the data. The classification of the antenna is based on the specifications like frequency, polarization, radiation, etc. In this we will observe some important point about microwave antenna in communication network, relay stations, transmission system, interconnection cable and inter-operations performing as an integrated whole. KEYWORDS: Microwave Antenna, Types of Antenna, Properties of Antenna, Applications of Antenna. I. INTRODUCTION The main purpose of this research to help people know many things about microwave antenna use in communication system. Microwaves are widely used for point-to-point communications because their small wavelength allows conveniently-sized antennas to direct them in narrow beams, which can be pointed directly at the receiving antenna. This allows nearby microwave equipment to use the same frequencies without interfering with each other, as lower frequency radio waves do. -

DOCSIS 3.0 Physical Layer Specification
Data-Over-Cable Service Interface Specifications DOCSIS® 3.0 Physical Layer Specification CM-SP-PHYv3.0-C01-171207 CLOSED Notice This DOCSIS specification is the result of a cooperative effort undertaken at the direction of Cable Television Laboratories, Inc. for the benefit of the cable industry and its customers. You may download, copy, distribute, and reference the documents herein only for the purpose of developing products or services in accordance with such documents, and educational use. Except as granted by CableLabs® in a separate written license agreement, no license is granted to modify the documents herein (except via the Engineering Change process), or to use, copy, modify or distribute the documents for any other purpose. This document may contain references to other documents not owned or controlled by CableLabs. Use and understanding of this document may require access to such other documents. Designing, manufacturing, distributing, using, selling, or servicing products, or providing services, based on this document may require intellectual property licenses from third parties for technology referenced in this document. To the extent this document contains or refers to documents of third parties, you agree to abide by the terms of any licenses associated with such third-party documents, including open source licenses, if any. © Cable Television Laboratories, Inc., 2006 - 2017 CM-SP-PHYv3.0-C01-171207 Data-Over-Cable Service Interface Specifications DISCLAIMER This document is furnished on an "AS IS" basis and neither CableLabs nor its members provides any representation or warranty, express or implied, regarding the accuracy, completeness, noninfringement, or fitness for a particular purpose of this document, or any document referenced herein. -

Inexpensive Microwave Antenna Demonstrations Based on the IEEE Presentation by John Kraus – Jon Wallace
Inexpensive Microwave Antenna Demonstrations Based on the IEEE Presentation by John Kraus – Jon Wallace Abstract: After seeing a video of John Kraus giving a demonstration on radio antennas to the IEEE many years ago, the author was so inspired that he researched the concepts and sought to reproduce as much of the demonstration as he could. It is hoped that these demonstrations will educate and inspire others to explore as well. They cover topics which include: beam width, inverse square law, polarization, reflection, refraction, interference, absorption, gain, wave guides, diffraction, and more. The equipment used consists of a Gunn diode source with horn antenna and a WR-90 horn antenna with crystal detector, instrumentation amplifier, and voltage controlled oscillator (VCO) so that changes in intensity will be heard as pitch changes. Safety Although these microwave frequencies are not the ones used for cooking, they can still cause damage to eyes and sensitive areas of the body. When I started this project I searched for the most stringent safety recommendations I could find for a 10 mW transmitter at about 10 GHz. This recommendation was to keep a minimum distance of 60 cm. (2 ft.). I also designed an aluminum-screened mask that can be worn when presenting the demonstrations. It completely blocks all radiation from the transmitter. Close-up pictures and hints on making one are included at the end of this document. Stay safe! The Equipment The various demonstration devices will be described in each section and building tips are included at the end of the paper. The basic equipment consists of a transmitter (a Gunn diode device) with a larger horn and regulated 8V power supply powered by a 9V battery, a receiver with a small horn antenna, crystal detector, instrumentation amplifier, voltage controlled oscillator, and powerful speaker. -

Simple Antenna Can Help Kick Costly Cable TV Habit
Simple antenna can help kick costly cable TV habit By Gregory Karp, Chicago Tribune [email protected] Terrain, trees and buildings can affect signals and the type of antenna that works best at your location. (Comstock Images) As more people rethink ways to get television programming outside the traditional cable and satellite companies, the unsung TV antenna is becoming a fundamental component of their cord-cutting strategy. That makes sense. Not only are broadcast TV signals free, but even a simple antenna can produce the best picture you've ever seen on your TV because the high-definition signals are less compressed than through cable or satellite. And new flat, wall-mounted indoor antennas are a cinch to install and far less offensive aesthetically than the old rabbit ears — some can be affixed to a window behind drapes, for example. And with a one-time cost of about $50 for about 50 channels — including almost all of the most popular 50 shows — the switch is a frugal- spender's delight. HBO recently announced it would offer streaming online HBO service without a cable or satellite subscription, removing yet another reason people remain tethered to a paid-TV provider. ESPN, perhaps the largest hurdle to cutting cords, reportedly is looking into the same thing. Antenna sales spiked several years ago with the switch to digital broadcast signals, but the antenna business has continued to flourish, said Ian Geise, senior vice president of Voxx Accessories, the largest seller of TV antennas under such names as Terk and RCA. "It's really been this shift in mindset for people and (their) television entertainment," he said. -

AWS Microwave Antenna System Relocation Kit
AWS Microwave Antenna System Relocation Kit Key Products for 18 GHz Point-to-Point Applications The Clear Choice™ Radio Frequency Systems is the wireless Contact Information and broadcast infrastructure company Radio Frequency Systems with the strength and resources to serve 200 Pondview Drive the global market with a commanding Meriden, CT 06450 USA array of antenna systems and sub-system Sales & Customer Support solutions. Phone: (203) 630-3311 (800) 321-4700 (Toll-Free USA & Canada) RFS spans the continents with strategically Fax: (203) 634-2272 Email: [email protected] located operations, encompassing design, Catalog/Literature manufacturing, distribution, sales and Phone: (877) RFSWORLD service operations for markets in North Email: [email protected] America, South America, Europe, Africa, Technical Support the Middle East, Australia, Southeast Asia Phone: (203) 630-3311 x1880 (800) 659-1880 (Toll-Free USA & Canada) and China. Email: [email protected] Radio Frequency Systems brings a long tra- dition of design, engineering and manu- facturing expertise to carriers, OEMs, dis- Table of Contents tributors and systems integrators in the broadcast, cellular, land-mobile, Model Number Description Page microwave and government markets. Solid Parabolic Microwave Antennas SB2-190BB CompactLine Antenna, Single Polarized, 2 ft . .1 SU4-190AZ SlimLine Ultra High Performance Antenna, Single Polarized, 4 ft . .5 SU6-190BZ SlimLine Ultra High Performance Antenna, Single Polarized, 6 ft . .9 SUX2-190BB SlimLine Ultra High Performance Antenna, Dual Polarized, 2 ft . .13 SUX4-190AZ SlimLine Ultra High Performance Antenna, Dual Polarized, 4 ft . .17 UXA4-190AZ High Cross Polar Discrimination, Dual Polarized, 4 ft . .21 UXA6-190BZ High Cross Polar Discrimination, Dual Polarized, 6 ft . -

Chapter 1: Modulation Systems
SYLLABUS: 141304 – ANALOG AND DIGITAL COMMUNICATION L T P C 3 1 0 4 UNIT I FUNDAMENTALS OF ANALOG COMMUNICATION 9 Principles of Amplitude Modulation – AM Envelope – Frequency Spectrum and Bandwidth – Modulation Index and Percent Modulation – AM Voltage Distribution – AM Power Distribution – Angle Modulation – FM and PM Waveforms – Phase Deviation and Modulation Index – Frequency Deviation and Percent Modulation – Frequency Analysis of Angle Modulated Waves – Bandwidth Requirements for Angle Modulated Waves. UNIT II DIGITAL COMMUNICATION 9 Basics – Shannon Limit for Information Capacity – Digital Amplitude Modulation – Frequency Shift Keying – FSK Bit Rate and Baud – FSK Transmitter – BW Consideration of FSK – FSK Receiver – Phase Shift Keying – Binary Phase Shift Keying – QPSK – Quadrature Amplitude Modulation – Bandwidth Efficiency – Carrier Recovery – Squaring Loop – Costas Loop – DPSK. UNIT III DIGITAL TRANSMISSION 9 Basics – Pulse Modulation – PCM – PCM Sampling – Sampling Rate – Signal to Quantization Noise Rate – Companding – Analog and Digital – Percentage Error – Delta Modulation – Adaptive Delta Modulation – Differential Pulse Code Modulation – Pulse Transmission – Intersymbol Interference – Eye Patterns. UNIT IV DATA COMMUNICATIONS 9 Basics – History of Data Communications – Standards Organizations for Data Communication – Data Communication Circuits – Data Communication Codes – Error Control – Error Detection – Error Correction – Data Communication Hardware – Serial and Parallel Interfaces – Data Modems – Asynchronous Modem – Synchronous Modem – Low-Speed Modem – Medium and High Speed Modem – Modem Control. UNIT V SPREAD SPECTRUM AND MULTIPLE ACCESS TECHNIQUES 9 Basics – Pseudo-Noise Sequence – DS Spread Spectrum with Coherent Binary PSK – Processing Gain – FH Spread Spectrum – Multiple Access Techniques – Wireless Communication – TDMA and CDMA in Wireless Communication Systems – Source Coding of Speech for Wireless Communications. L: 45 T: 15 Total: 60 TEXT BOOKS 1.