DOCSLIB.ORG

Generalized Perfect Numbers

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Generalized Perfect Numbers COMMENTATIONES MATHEMATICAE Vol. 53, No. 1 (2013), 61-72 D.P. Shukla, Shikha Yadav Generalized Perfect Numbers Abstract. In this paper a modified form of perfect numbers called (p, q)+ perfect numbers and their properties with examples have been discussed. Further properties of σ+ arithmetical function have been discussed and on its basis a modified form of perfect number called (p, q)+ super perfect numbers have been discussed. A modified form of perfect number called (p, 0)-perfect and their characterization has been stu- died. In the end of this paper almost super perfect numbers have been introduced. 2000 Mathematics Subject Classification: 11A25. Key words and phrases: Prime numbers, perfect numbers, super perfect numbers, Arithmetical Functions . 1. (p, q)+perfect numbers. In J. Sandor and K. Atanassov [4] (p, q) perfect numbers with their properties and examples have been discussed. G.L. Cohen H.J.J. te Ride [1] called the natural number n , (p, q) perfect number if (1.1) σp(n) = qn, where σp(n) = σ(σ(...(σ(n)...))). p times − In this paper we will discuss one more| {z type} of modified perfect numbers called (p, q)+perfect numbers. A natural number n is called (p, q)+perfect numbers if p (1.2) σ+(n) = qn, where p σ+(n) = σ+(σ+(...(σ+(n)...))). p times − | {z } 62 Generalized Perfect Numbers Here, σ+ denotes the sum of all even divisors of n. Since, σ+(n) denotes the sum of all even divisors of n therefore, σ+(n) = 0 if n is odd. Hence (p, q)+ perfect numbers are defined for only even numbers. Further, if n is even, n = 2k.N, k 1 with N odd, then ­ σ (n) = 2(2k 1)σ(N). + − Let n = 2, as σ+(2) = 2 so, σ+(σ+(2)) = 2 . Now take p = 3 σ+(σ+(σ+(2))) = σ+(σ+(2)) = 2, for p = 4, σ+(σ+(σ+(σ+(2)))) = 2. By induction, we can see that σp (2) = 2 = 1 2, for all p 1 + × ­ Hence n = 2 is the solution for (p, 1)+ perfect numbers Some examples of (p, q)+ perfect numbers for p 21 have been given in the tables as follows ¬ Let n = 4 Let n = 6 Table -1.1 Table -1.2 p p p σ+ q n p σ+ q n 1 6 - × 1 8 - × 2 8 2 4 2 14 - 3 14 - × 3 16 - 4 16 4 4 4 30 5 6 5 30 - × 5 48 8×6 6 48 12 4 6 120 20× 6 7 120 30×4 7 336 56×6 8 336 84×4 8 960 160× 6 9 960 240× 4 9 3024 504×6 10 3024 756×4 10 9600 1600× 6 11 9600 2400× 4 11 31496 - × 12 31496 7874×4 12 57344 - 13 57344 14336× 4 13 131056 - 14 131056 32764×4 14 245760 40960 6 15 245760 61440×4 15 786384 131064× 6 16 786384 196596× 4 16 2130180 355030×6 17 2130180 532545×4 17 5507712 917952×6 18 5507712 1376928× 4 18 18068544 3011424× 6 19 18068544 4517136×4 19 58705920 9784320×6 20 58705920 14676480× 4 20 110046720 18341120× 6 21 110046720 27511680×4 21 423843840 70640640×6 × × D.P. Shukla, S. Yadav 63 Let n = 8 Let n = 10 Table -1.3 Table-1.4 p p p σ+ q n p σ+ q n 1 14 - × 1 12 - × 2 16 2 8 2 24 - 3 30 - × 3 56 - 4 48 6 8 4 112 - 5 120 15× 8 5 240 24 10 6 336 42×8 6 720 72×10 7 960 120× 8 7 2340 234× 10 8 3024 378×8 8 6552 - × 9 9600 1200× 8 9 20384 10 31496 3937×8 10 49476 -− 11 57344 7168×8 11 122880 12288 10 12 131056 16382× 8 12 393168 - × 13 245760 30720×8 13 983040 98304 10 14 786384 98298×8 14 3145680 314568× 10 15 2130180 2662725× 8 15 10866960 1086696× 10 16 5507712 688464 ×8 16 40360320 4036032×10 17 18068544 2258568× 8 17 189719712 - × 18 58705920 7338240×8 18 711065600 71106560 10 19 110046720 13755840× 8 19 2080358912 - × 20 423843840 52980480×8 20 4286578688 - × Let n=12 Let n=14 Table=1.5 Table = 1..6 p p p σ+ q n p σ+ q n 1 24 2 ×12 1 16 - × 2 56 - × 2 30 - 3 112 - 3 48 - 4 240 20 12 4 120 - 5 720 60×12 5 336 24 14 6 2340 195× 12 6 960 - × 7 6552 546×12 7 3024 216 14 8 20384 - × 8 9600 - × 9 49476 4123 12 9 31496 10 122880 10240× 12 10 57344 4096− 14 11 393168 32764×12 11 131056 - × 12 983040 81920×12 12 245760 - 13 3145680 262140× 12 13 786384 - 14 10866960 905580×12 14 2130180 - 15 40360320 3363360× 12 15 5507712 393408 14 16 189719712 15809976× 12 16 18068544 - × 17 711065600 - × 17 58705920 4193280 14 18 2080358912 - 18 110046720 7860480×14 19 4286578688 - 19 423843840 30274560× 14 × 64 Generalized Perfect Numbers From the tables given above it is clear that all (2,2)+ perfect numbers coincide with + super perfect numbers and (1,2)+ perfect numbers coincide with + perfect numbers. Before discussing the properties of (p, q)+ perfect numbers let us discuss some properties of σ and σ+ given as follows For all positive integers n 2 one has ­ (1.3) σ(n) n + 1, ­ with equality only for n =prime. Similarly (1.4) σ(n) n, ­ with equality only for n = 1. For all positive integers m, n (1.5) σ (mn) mσ (n), + ­ + with equality only for m = 1, m and n both odd. (1.6) σ (mn) σ (m)σ (n), + ­ + + with equality only for m and n both odd. For an even positive integer n (1.7) σ (n) n, + ­ with equality only for n = 2, if n > 2 then, (1.8) σ+(n) > n + 1. Theorem 1.1. For every n 4 ­ σ (σ (n)) 2n + + ­ Proof. Let n = 2, then σ (σ (2)) = 2 < 2 2 = 4. + + × Take n 4. Since, σ+(n) = 0 for n is odd therefore,­ n is always even. If n is even then n =2k.m, with m is odd. Now k k k σ+(σ+(2 .m)) = σ+(2(2 1)σ(m)) σ(m)σ+(2(2 1)) (using 1.5). So, using (1.3) and (1.5),− we have ­ − σ(m)σ (2(2k 1) = 2σ(m)σ(2k 1) 2mσ(2k 1) 2m2k = 2n. + − − ­ − ­ D.P. Shukla, S. Yadav 65 Hence σ (σ (n)) 2n, for every n 4. + + ­ ­ Now using theorem 1.1, we have σ (σ (σ (σ (n)))) 2σ (σ (n)) 2.2n = 4n. + + + + ­ + + ­ So, (1.9) σ4 (n) 4n. + ­ Similarly, using inequation (1.9) and theorem 1.1 σ6 (n) = σ (σ (σ (σ (σ (σ (n)))))) 4(σ (σ (n)) 4.2n = 8n > 6n. + + + + + + + ­ + + ­ So, 6 (1.10) σ+(n) > 6n. Therefore by induction we can prove that Theorem 1.2. For every even positive integer p 2 and n 4 ­ ­ σp (n) pn + ­ Theorem 1.3. n is (2, 2)+ perfect number if and only if it has the form n = 2k, where 2k 1 is a prime. Proof. It− is clear that (2, 2)+ perfect numbers coincide with the + super perfect numbers. In J. Sandor and E. Egri [2] it has been proved that n is + super perfect if and only if it has the form n = 2k, where 2k 1 is a prime. Hence theorem is proved. − 2. (p, q)+ super perfect numbers. J. Sandor and K. Atanssov [3] have defined (p, q) super perfect numbers as follows- Given two positive integers p and q, a number n N is said to be (p, q) super perfect if it satisfies ∈ (2.1) σ(pσ(n)) = qn, where σ(n) is a divisor function which is the sum of different divisors of n. n N, n > 1. ∈ σ(1) = 1 and (2.2) σ(n) = d, Xd/n 66 Generalized Perfect Numbers for all n 1, σ(n) n and σ(n) n + 1 for n 2,with equality holds only for n is prime. ­ ­ ­ ­ Let σ+(n) denotes the sum of all even divisors of n. We say that a positive integer n is called + perfect number if (2.3) σ+(n) = 2n. J. Sandor and E. Egri [2] have proved a result defined as follows k Lemma 2.1: If n is odd, then σ+(n) = 0. If n is even, n = 2 N, k 1 with N odd then ­ σ (n) = 2(2k 1)σ(N). + − A positive integer n is called + super perfect if (2.4) σ+(σ+(n)) = 2n, for two positive integers p and q we have defined (p, q)+super perfect numbers as follows Given two positive integers p and q a number n N is said to be (p, q)+ super perfect number if it satisfies. ∈ (2.5) σ+(pσ+(n)) = qn. Theorem 2.2 The single (1, 1)+ super perfect number is n = 2 Proof.Let n is (1, 1)+super perfect number then by equation, (2.5) σ+(σ+(n)) = n, using (1.7) σ (σ (n)) σ (n). + + ­ + So, (2.6) n σ (n). ­ + Further, using (1.7) we obtain (2.7) σ (n) n. + ­ From (2.6) and (2.7) we get, D.P. Shukla, S. Yadav 67 σ+(n) = n. Since equality in (1.7), holds only for n = 2. Hence n = 2 is single (1,1)+super perfect number. Theorem 2.3. If n is (p, q)+ super perfect number then n = 2kN be an even positive integer where N is odd positive integer and k 1 ­ Proof.
Load more

Recommended publications
  • Input for Carnival of Math: Number 115, October 2014
    Input for Carnival of Math: Number 115, October 2014 I visited Singapore in 1996 and the people were very kind to me. So I though this might be a little payback for their kindness. Good Luck. David Brooks The “Mathematical Association of America” (http://maanumberaday.blogspot.com/2009/11/115.html ) notes that: 115 = 5 x 23. 115 = 23 x (2 + 3). 115 has a unique representation as a sum of three squares: 3 2 + 5 2 + 9 2 = 115. 115 is the smallest three-digit integer, abc , such that ( abc )/( a*b*c) is prime : 115/5 = 23. STS-115 was a space shuttle mission to the International Space Station flown by the space shuttle Atlantis on Sept. 9, 2006. The “Online Encyclopedia of Integer Sequences” (http://www.oeis.org) notes that 115 is a tridecagonal (or 13-gonal) number. Also, 115 is the number of rooted trees with 8 vertices (or nodes). If you do a search for 115 on the OEIS website you will find out that there are 7,041 integer sequences that contain the number 115. The website “Positive Integers” (http://www.positiveintegers.org/115) notes that 115 is a palindromic and repdigit number when written in base 22 (5522). The website “Number Gossip” (http://www.numbergossip.com) notes that: 115 is the smallest three-digit integer, abc, such that (abc)/(a*b*c) is prime. It also notes that 115 is a composite, deficient, lucky, odd odious and square-free number. The website “Numbers Aplenty” (http://www.numbersaplenty.com/115) notes that: It has 4 divisors, whose sum is σ = 144.
    [Show full text]
  • A Study of .Perfect Numbers and Unitary Perfect
    CORE Metadata, citation and similar papers at core.ac.uk Provided by SHAREOK repository A STUDY OF .PERFECT NUMBERS AND UNITARY PERFECT NUMBERS By EDWARD LEE DUBOWSKY /I Bachelor of Science Northwest Missouri State College Maryville, Missouri: 1951 Master of Science Kansas State University Manhattan, Kansas 1954 Submitted to the Faculty of the Graduate College of the Oklahoma State University in partial fulfillment of .the requirements fqr the Degree of DOCTOR OF EDUCATION May, 1972 ,r . I \_J.(,e, .u,,1,; /q7Q D 0 &'ISs ~::>-~ OKLAHOMA STATE UNIVERSITY LIBRARY AUG 10 1973 A STUDY OF PERFECT NUMBERS ·AND UNITARY PERFECT NUMBERS Thesis Approved: OQ LL . ACKNOWLEDGEMENTS I wish to express my sincere gratitude to .Dr. Gerald K. Goff, .who suggested. this topic, for his guidance and invaluable assistance in the preparation of this dissertation. Special thanks.go to the members of. my advisory committee: 0 Dr. John Jewett, Dr. Craig Wood, Dr. Robert Alciatore, and Dr. Vernon Troxel. I wish to thank. Dr. Jeanne Agnew for the excellent training in number theory. that -made possible this .study. I wish tc;, thank Cynthia Wise for her excellent _job in typing this dissertation •. Finally, I wish to express gratitude to my wife, Juanita, .and my children, Sondra and David, for their encouragement and sacrifice made during this study. TABLE OF CONTENTS Chapter Page I. HISTORY AND INTRODUCTION. 1 II. EVEN PERFECT NUMBERS 4 Basic Theorems • • • • • • • • . 8 Some Congruence Relations ••• , , 12 Geometric Numbers ••.••• , , , , • , • . 16 Harmonic ,Mean of the Divisors •. ~ ••• , ••• I: 19 Other Properties •••• 21 Binary Notation. • •••• , ••• , •• , 23 III, ODD PERFECT NUMBERS . " . 27 Basic Structure • , , •• , , , .
    [Show full text]
  • Newsletter No. 31 March 2004
    Newsletter No. 31 March 2004 Welcome to the second newsletter of 2004. We have lots of goodies for you this month so let's get under way. Maths is commonly said to be useful. The variety of its uses is wide but how many times as teachers have we heard students exclaim, "What use will this be when I leave school?" I guess it's all a matter of perspective. A teacher might say mathematics is useful because it provides him/her with a livelihood. A scientist would probably say it's the language of science and an engineer might use it for calculations necessary to build bridges. What about the rest of us? A number of surveys have shown that the majority of us only need to handle whole numbers in counting, simple addition and subtraction and decimals as they relate to money and domestic measurement. We are adept in avoiding arithmetic - calculators in their various forms can handle that. We prefer to accept so-called ball-park figures rather than make useful estimates in day-to-day dealings and computer software combined with trial-and-error takes care of any design skills we might need. At the same time we know that in our technological world numeracy and computer literacy are vital. Research mathematicians can push boundaries into the esoteric, some of it will be found useful, but we can't leave mathematical expertise to a smaller and smaller proportion of the population, no matter how much our students complain. Approaching mathematics through problem solving - real and abstract - is the philosophy of the nzmaths website.
    [Show full text]
  • The Schnirelmann Density of the Set of Deficient Numbers
    THE SCHNIRELMANN DENSITY OF THE SET OF DEFICIENT NUMBERS A Thesis Presented to the Faculty of California State Polytechnic University, Pomona In Partial Fulfillment Of the Requirements for the Degree Master of Science In Mathematics By Peter Gerralld Banda 2015 SIGNATURE PAGE THESIS: THE SCHNIRELMANN DENSITY OF THE SET OF DEFICIENT NUMBERS AUTHOR: Peter Gerralld Banda DATE SUBMITTED: Summer 2015 Mathematics and Statistics Department Dr. Mitsuo Kobayashi Thesis Committee Chair Mathematics & Statistics Dr. Amber Rosin Mathematics & Statistics Dr. John Rock Mathematics & Statistics ii ACKNOWLEDGMENTS I would like to take a moment to express my sincerest appreciation of my fianc´ee’s never ceasing support without which I would not be here. Over the years our rela­ tionship has proven invaluable and I am sure that there will be many more fruitful years to come. I would like to thank my friends/co-workers/peers who shared the long nights, tears and triumphs that brought my mathematical understanding to what it is today. Without this, graduate school would have been lonely and I prob­ ably would have not pushed on. I would like to thank my teachers and mentors. Their commitment to teaching and passion for mathematics provided me with the incentive to work and succeed in this educational endeavour. Last but not least, I would like to thank my advisor and mentor, Dr. Mitsuo Kobayashi. Thanks to his patience and guidance, I made it this far with my sanity mostly intact. With his expertise in mathematics and programming, he was able to correct the direction of my efforts no matter how far they strayed.
    [Show full text]
  • Arxiv:2106.08994V2 [Math.GM] 1 Aug 2021 Efc Ubr N30b.H Rvdta F2 If That and Proved Properties He Studied BC
    Measuring Abundance with Abundancy Index Kalpok Guha∗ Presidency University, Kolkata Sourangshu Ghosh† Indian Institute of Technology Kharagpur, India Abstract A positive integer n is called perfect if σ(n) = 2n, where σ(n) denote n σ(n) the sum of divisors of . In this paper we study the ratio n . We de- I → I n σ(n) fine the function Abundancy Index : N Q with ( ) = n . Then we study different properties of Abundancy Index and discuss the set of Abundancy Index. Using this function we define a new class of num- bers known as superabundant numbers. Finally we study superabundant numbers and their connection with Riemann Hypothesis. 1 Introduction Definition 1.1. A positive integer n is called perfect if σ(n)=2n, where σ(n) denote the sum of divisors of n. The first few perfect numbers are 6, 28, 496, 8128, ... (OEIS A000396), This is a well studied topic in number theory. Euclid studied properties and nature of perfect numbers in 300 BC. He proved that if 2p −1 is a prime, then 2p−1(2p −1) is an even perfect number(Elements, Prop. IX.36). Later mathematicians have arXiv:2106.08994v2 [math.GM] 1 Aug 2021 spent years to study the properties of perfect numbers. But still many questions about perfect numbers remain unsolved. Two famous conjectures related to perfect numbers are 1. There exist infinitely many perfect numbers. Euler [1] proved that a num- ber is an even perfect numbers iff it can be written as 2p−1(2p − 1) and 2p − 1 is also a prime number.
    [Show full text]
  • Arxiv:2008.10398V1 [Math.NT] 24 Aug 2020 Children He Has
    JOURNAL OF THE AMERICAN MATHEMATICAL SOCIETY Volume 00, Number 0, Pages 000{000 S 0894-0347(XX)0000-0 RECURSIVELY ABUNDANT AND RECURSIVELY PERFECT NUMBERS THOMAS FINK London Institute for Mathematical Sciences, 35a South St, London W1K 2XF, UK Centre National de la Recherche Scientifique, Paris, France The divisor function σ(n) sums the divisors of n. We call n abundant when σ(n) − n > n and perfect when σ(n) − n = n. I recently introduced the recursive divisor function a(n), the recursive analog of the divisor function. It measures the extent to which a number is highly divisible into parts, such that the parts are highly divisible into subparts, so on. Just as the divisor function motivates the abundant and perfect numbers, the recursive divisor function motivates their recursive analogs, which I introduce here. A number is recursively abundant, or ample, if a(n) > n and recursively perfect, or pristine, if a(n) = n. There are striking parallels between abundant and perfect numbers and their recursive counterparts. The product of two ample numbers is ample, and ample numbers are either abundant or odd perfect numbers. Odd ample numbers exist but are rare, and I conjecture that there are such numbers not divisible by the first k primes|which is known to be true for the abundant numbers. There are infinitely many pristine numbers, but that they cannot be odd, apart from 1. Pristine numbers are the product of a power of two and odd prime solutions to certain Diophantine equations, reminiscent of how perfect numbers are the product of a power of two and a Mersenne prime.
    [Show full text]
  • Integer Sequences
    UHX6PF65ITVK Book > Integer sequences Integer sequences Filesize: 5.04 MB Reviews A very wonderful book with lucid and perfect answers. It is probably the most incredible book i have study. Its been designed in an exceptionally simple way and is particularly just after i finished reading through this publication by which in fact transformed me, alter the way in my opinion. (Macey Schneider) DISCLAIMER | DMCA 4VUBA9SJ1UP6 PDF > Integer sequences INTEGER SEQUENCES Reference Series Books LLC Dez 2011, 2011. Taschenbuch. Book Condition: Neu. 247x192x7 mm. This item is printed on demand - Print on Demand Neuware - Source: Wikipedia. Pages: 141. Chapters: Prime number, Factorial, Binomial coeicient, Perfect number, Carmichael number, Integer sequence, Mersenne prime, Bernoulli number, Euler numbers, Fermat number, Square-free integer, Amicable number, Stirling number, Partition, Lah number, Super-Poulet number, Arithmetic progression, Derangement, Composite number, On-Line Encyclopedia of Integer Sequences, Catalan number, Pell number, Power of two, Sylvester's sequence, Regular number, Polite number, Ménage problem, Greedy algorithm for Egyptian fractions, Practical number, Bell number, Dedekind number, Hofstadter sequence, Beatty sequence, Hyperperfect number, Elliptic divisibility sequence, Powerful number, Znám's problem, Eulerian number, Singly and doubly even, Highly composite number, Strict weak ordering, Calkin Wilf tree, Lucas sequence, Padovan sequence, Triangular number, Squared triangular number, Figurate number, Cube, Square triangular
    [Show full text]
  • Multiplicatively Perfect and Related Numbers
    Journal of Rajasthan Academy of Physical Sciences ISSN : 0972-6306; URL : http://raops.org.in Vol.15, No.4, December, 2016, 345-350 MULTIPLICATIVELY PERFECT AND RELATED NUMBERS Shikha Yadav* and Surendra Yadav** *Department of Mathematics and Astronomy, University of Lucknow, Lucknow- 226007, U.P., India E-mail: [email protected] **Department of Applied Mathematics, Babasaheb Bhimrao Ambedkar University, Lucknow-226025, U.P., India, E-mail: ssyp_ [email protected] Abstract: Sandor [4] has discussed multiplicatively perfect (푀perfect) and multiplicatively +perfect numbers (called as 푀 +perfect). In this paper, we have discussed a new perfect number called as multiplicatively – perfect numbers (also called as 푀 − perfect). Further we study about Abundant, Deficient, Harmonic and Unitary analogue of harmonic numbers. Keywords and Phrases: Multiplicatively perfect numbers, Abundant numbers, Deficient numbers, Harmonic numbers and unitary divisor. 2010 Mathematics Subject Classification: 11A25. 1. Introduction Sandor and Egri [3], Sandor [4] have defined multiplicatively perfect and multiplicatively + perfect numbers as follows, A positive integer 푛 ≥ 1 is called multiplicatively perfect if 푅 푛 = 푛2, (1) where, 푅 푛 is product of divisor function. Let 푑1, 푑2, 푑3, … 푑푟 are the divisors of 푛 then 푅 푛 = 푑1. 푑2. 푑3. … 푑푟 . 푑(푛 ) Also, 푅 푛 = 푛 2 (2) Let 푅+(푛) denotes the product of even divisors of 푛. We say that 푛 is 푀 + perfect number if 2 푅+ 푛 = 푛 . (3) Now, in this paper we define 푀 − perfect numbers as follows, let 푅− 푛 denotes the product of odd divisors of 푛 .We say that 푛 is 푀 − perfect if 346 Shikha Yadav and Surendra Yadav 2 푅− 푛 = 푛 .
    [Show full text]
  • The Humble Sum of Remainders Function
    DRAFT VOL. 78, NO. 4, OCTOBER 2005 1 The Humble Sum of Remainders Function Michael Z. Spivey Samford University Birmingham, Alabama 35229 [email protected] The sum of divisors function is one of the fundamental functions in elementary number theory. In this note, we shine a little light on one of its lesser-known rela- tives, the sum of remainders function. We do this by illustrating how straightforward variations of the sum of remainders can 1) provide an alternative characterization for perfect numbers, and 2) help provide a formula for sums of powers of the first n posi- tive integers. Finally, we give a brief discussion of perhaps why the sum of remainders function, despite its usefulness, is less well known than the sum of divisors function. Some notation is in order. The standard notation for the sum of divisors function is σ(n): X σ(n) = d: djn We denote the sum of remainders function by ½(n), namely, Xn ½(n) = n mod d: d=1 Sums of remainders and perfect numbers A perfect number is a number equal to the sum of its positive divisors excluding itself. Another way to express this is that perfect numbers are those such that σ(n) = 2n. The three smallest perfect numbers are 6; 28, and 496. Euclid proved that every number of the form 2p¡1(2p ¡ 1); where p and 2p ¡ 1 are prime, is perfect. Euler proved the converse, that numbers of this form are the only even perfect numbers [3, p. 59]. One of the famous unsolved problems in number theory is whether or not there are any odd perfect numbers.
    [Show full text]
  • Techsparx Java Tuitions
    TechSparxJavaTuitionsTechSparxJavaJava Question Bank TuitionsTechSparxJavaTuitionsTechSp arxJavaTuitionsTechSparxJavaTuitions TechSparxJavaTuitionsTechSparxJavaTechSparx Java Tuitions “Better than a thousand days of diligent study is one day with a Great Teacher” TuitionsTechSparxJavaTuitionsTechSp Java Question Bank (version 5.3) arxJavaTuitionsTechSparxJavaTuitionshttp://techsparx.webs.com/ Saravanan.G TechSparxJavaTuitionsTechSparxJava TuitionsTech SparxJavaTuitionsTechSp arxJavaTuitionsTechSparxJavaTuitions TechSparxJavaTuitionsTechSparxJava TuitionsTechSparxJavaTuitionsTechSp arxJavaTuitionsTechSparxJavaTuitions TechSparxJavaTuitionsTechSparxJava TuitionsTechSparxJavaTuitionsTechSp arxJavaTuitionsTechSparxJavaTuitions TechSparxJavaTuitionsTechSparxJava TuitionsTechSparxJavaTuitionsTechSp Contents Modularization ........................................................................................................................................ 3 Most Simplest ......................................................................................................................................... 4 Decision Making Statements ................................................................................................................... 5 Switch Statement .................................................................................................................................... 6 Looping Constructs .................................................................................................................................
    [Show full text]
  • 15 Fifteen XV
    15 Fifteen XV i ii iii iiii iiiii Corresponding ordinal: fifteenth. The number 15 = 1 + 2 + 3 + 4 + 5 is a triangle (see above). If you play pool, you know this. The number 15 is the eighth odd number and the eighth composite number. As a product of primes: 15 = 3 5. · The number 15 has four divisors: 1, 3, 5, 15. The number 15 is the thirteenth deficient number: s(15) = 1 + 3 + 5 + 9 < 15. As the sum of four or fewer squares: 15 = 12 + 12 + 22 + 32. As the sum of nine or fewer cubes: 15 = 7 13 + 23. The number 15 is the first of only · 15 numbers that can be written as the sum of eight cubes, but no fewer. The others are 22, 50, 114, 167, 175, 186, 212, 231, 238, 303, 364, 420, 428, and 454. As the difference of two squares: 15 = 42 12 = 82 72. The number 15 occurs in five Pythagorean triples: [8, 15, 17], [9, 12, 15], [15, 20, 25], [15, 36, 39], [15, 112, 113]. The first and the last are primitive. As a sum of three odd primes: 3 + 5 + 7 and 5 + 5 + 5 There are 15 three-digit prime palindromes: 101, 131, 151, 181, 191, 313, 353, 373, 383, 727, 757, 787, 797, 919, and 929. There are 1 + 5 primes less than 15. (Prime Curios) The number 15 is the smallest emirpimes, a number that is the product of two primes (a semiprime) whose reversal (51) is also the product of two primes. The fifteenth President of the United States was James Buchanan.
    [Show full text]
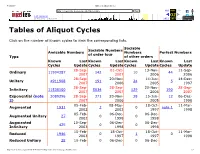
  • Tables of Aliquot Cycles
    5/29/2017 Tables of Aliquot Cycles http://amicable.homepage.dk/tables.htm Go FEB MAY JUN f ❎ 117 captures 02 ⍰ ▾ About 28 May 2002 ‑ 2 May 2014 2012 2014 2015 this capture Tables of Aliquot Cycles Click on the number of known cycles to view the corresponding lists. Sociable Sociable Numbers Amicable Numbers Numbers Perfect Numbers of order four Type of other orders Known Last Known Last Known Last Known Last Cycles Update Cycles Update Cycles Update Cycles Update 28­Sep­ 01­Oct­ 13­Nov­ 11­Sep­ Ordinary 11994387 142 10 44 2007 2007 2006 2006 28­Sep­ 20­Nov­ 14­Jun­ 14­Dec­ Unitary 4911908 191 24 5 2007 2006 2005 1997 28­Sep­ 28­Sep­ 20­Nov­ 28­Sep­ Infinitary 11538100 5034 129 190 2007 2007 2006 2007 Exponential (note 3089296 28­Sep­ 371 20­Nov­ 38 15­Jun­ 12 06­Dec­ 2) 2007 2006 2005 1998 05­Feb­ 08­May­ 18­Oct­ 11­Mar­ Augmented 1931 2 0 note 1 2002 2003 1997 1998 05­Feb­ 06­Dec­ 06­Dec­ Augmented Unitary 27 0 0 2002 1998 1998 Augmented 10­Sep­ 06­Dec­ 06­Dec­ 425 0 0 Infinitary 2003 1998 1998 15­Feb­ 18­Oct­ 18­Oct­ 11­Mar­ Reduced 1946 0 1 0 2003 1997 1997 1998 Reduced Unitary 28 15­Feb­ 0 06­Dec­ 0 06­Dec­ http://web.archive.org/web/20140502102524/http://amicable.homepage.dk/tables.htm 1/3 5/29/2017 Tables of Aliquot Cycles http://amicable.homepage.dk/tables.htm2003 1998 Go 1998 FEB MAY JUN f ❎ 117 captures 10­Sep­ 06­Dec­ 06­Dec­ 02 ⍰ Reduced Infinitary 427 0 0 ▾ About 28 May 2002 ‑ 2 May 2014 2003 1998 1998 2012 2014 2015 this capture Note 1: All powers of 2 are augmented perfect numbers; no other augmented perfect numbers are known.
    [Show full text]