Navigational Algorithms
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Celestial Navigation Tutorial
NavSoft’s CELESTIAL NAVIGATION TUTORIAL Contents Using a Sextant Altitude 2 The Concept Celestial Navigation Position Lines 3 Sight Calculations and Obtaining a Position 6 Correcting a Sextant Altitude Calculating the Bearing and Distance ABC and Sight Reduction Tables Obtaining a Position Line Combining Position Lines Corrections 10 Index Error Dip Refraction Temperature and Pressure Corrections to Refraction Semi Diameter Augmentation of the Moon’s Semi-Diameter Parallax Reduction of the Moon’s Horizontal Parallax Examples Nautical Almanac Information 14 GHA & LHA Declination Examples Simplifications and Accuracy Methods for Calculating a Position 17 Plane Sailing Mercator Sailing Celestial Navigation and Spherical Trigonometry 19 The PZX Triangle Spherical Formulae Napier’s Rules The Concept of Using a Sextant Altitude Using the altitude of a celestial body is similar to using the altitude of a lighthouse or similar object of known height, to obtain a distance. One object or body provides a distance but the observer can be anywhere on a circle of that radius away from the object. At least two distances/ circles are necessary for a position. (Three avoids ambiguity.) In practice, only that part of the circle near an assumed position would be drawn. Using a Sextant for Celestial Navigation After a few corrections, a sextant gives the true distance of a body if measured on an imaginary sphere surrounding the earth. Using a Nautical Almanac to find the position of the body, the body’s position could be plotted on an appropriate chart and then a circle of the correct radius drawn around it. In practice the circles are usually thousands of miles in radius therefore distances are calculated and compared with an estimate. -

Concise Sight Reductin Tables From
11-36 Starpath Celestial Navigation Course Special Topics IN DEPTH... 11-37 11.11 Sight Reduction with the NAO Tables money and complexity in the long run by not having to bother with various sources of tables. With this in Starting in 1989, there was a significant change in the Location on table pages N S Declination mind, we have developed a work form that makes the Top Sides available tables for celestial navigation. As we have same + D° D' use of these tables considerably easier than just following sign B = sign Z learned so far, the tables required are an almanac Latitude N S LHA contrary - 1 and a set of sight reduction tables. In the past sight the instructions given in the almanac. With the use + if LHA = 0 to 90 SR Table A° A' + B° B' + Z1 - if LHA = 91 to 269 of our workform, the NAO tables do not take much 1 ------------------> - - reduction (SR) tables were usually chosen from Pub + if LHA = 270 to 360 249 (most popular with yachtsmen) and Pub 229 longer than Pub 249 does for this step of the work. F° F' Naturally, the first few times go slowly, but after a few which is required on USCG license exams. The latter bar top means rounded examples it becomes automatic and easy. The form value 30' or 0.5° rounds up have more precision, but this extra precision would guides you through the steps. + if F = 0 to 90 rarely affect the final accuracy of a celestial fix. Pub A F SR Table H° H' P° P' + Z2 2 ------------------> - - if F = 90 to 180 229 is much heavier, more expensive, and slightly We have included here a few of the earlier examples, more difficult to use. -

Chapter 19 Sight Reduction
CHAPTER 19 SIGHT REDUCTION BASIC PROCEDURES 1900. Computer Sight Reduction 1901. Tabular Sight Reduction The purely mathematical process of sight reduction is The process of deriving from celestial observations the an ideal candidate for computerization, and a number of information needed for establishing a line of position, different hand-held calculators, apps, and computer LOP, is called sight reduction. The observation itself con- programs have been developed to relieve the tedium of sists of measuring the altitude of the celestial body above working out sights by tabular or mathematical methods. the visible horizon and noting the time. The civilian navigator can choose from a wide variety of This chapter concentrates on sight reduction using the hand-held calculators and computer programs that require Nautical Almanac and Pub. No. 229: Sight Reduction Ta- only the entry of the DR position, measured altitude of the bles for Marine Navigation. Pub 229 is available on the body, and the time of observation. Even knowing the name NGA website. The method described here is one of many of the body is unnecessary because the computer can methods of reducing a sight. Use of the Nautical Almanac identify it based on the entered data. Calculators, apps, and and Pub. 229 provide the most precise sight reduction prac- computers can provide more accurate solutions than tabular tical, 0.'1 (or about 180 meters). and mathematical methods because they can be based on The Nautical Almanac contains a set of concise sight precise analytical computations rather than rounded values reduction tables and instruction on their use. It also contains inherent in tabular data. -

The Motion of the Observer in Celestial Navigation
The Motion of the Observer in Celestial Navigation George H. Kaplan U.S. Naval Observatory Abstract Conventional approaches to celestial navigation are based on the geometry of a sta- tionary observer. Any motion of the observer during the time observations are taken must be compensated for before a fix can be determined. Several methods have been developed that ac- count for the observer's motion and allow a fix to be determined. These methods are summarized and reviewed. Key Words celestial navigation, celestial fix, motion of observer Introduction The object of celestial navigation is the determination of the latitude and longitude of a vessel at a specific time, through the use of observations of the altitudes of celestial bodies. Each observation defines a circle of position on the surface of the Earth, and the small segment of the circle that passes near the observer's estimated position is represented as a line of position (LOP). A position fix is located at the intersection of two or more LOPs. This construction works for a fixed observer or simultaneous observations. However, if the observer is moving, the LOPs from two consecutive observations do not necessarily intersect at a point corresponding to the observer's position at any time; if three or more observations are involved, there may be no common intersection. Since celestial navigation normally involves a single observer on a moving ship, something has to be done to account for the change in the observer's position during the time required to take a series of observations. This report reviews the methods used to deal with the observer's motion. -

Intro to Celestial Navigation
Introduction to Celestial Navigation Capt. Alison Osinski 2 Introduction to Celestial Navigation Wow, I lost my charts, and the GPS has quit working. Even I don’t know where I am. Was is celestial navigation? Navigation at sea based on the observation of the apparent position of celestial bodies to determine your position on earth. What you Need to use Celestial Navigation (Altitude Intercept Method of Sight Reduction) 1. A sextant is used to measure the altitude of a celestial object, by taking “sights” or angular measurements between the celestial body (sun, moon, stars, planets) and the visible horizon to find your position (latitude and longitude) on earth. Examples: Astra IIIB $699 Tamaya SPICA $1,899 Davis Master Mark 25 $239 3 Price range: Under $200 - $1,900 Metal sextants are more accurate, heavier, need fewer adjustments, and are more expensive than plastic sextants, but plastic sextants are good enough if you’re just going to use them occasionally, or stow them in your life raft or ditch bag. Spend the extra money on purchasing a sextant with a whole horizon rather than split image mirror. Traditional sextants had a split image mirror which divided the image in two. One side was silvered to give a reflected view of the celestial body. The other side of the mirror was clear to give a view of the horizon. The advantage of a split image mirror is that the image may be slightly brighter because more light is reflected through the telescope. This is an advantage if you are going to take most of your shots of stars at twilight. -

Navigational Algorithms
NNAAVVIIGGAATTIIOONNAALL AALLGGOORRIITTHHMMSS SSiigghhtt RReedduuccttiioonn wwiitthh MMaattrriicceess © Andrés Ruiz San Sebastián – Donostia 43º 19’N 002ºW http://www.geocities.com/andresruizgonzalez 2 Índice Finding position by stars .............................................................................................................. 3 Two Observations........................................................................................................................ 3 Iteration for the assumed position ............................................................................................ 3 3 Observations............................................................................................................................. 4 n Observations............................................................................................................................. 4 Appendix A1. Algorithms ............................................................................................................................. 5 A2. Examples............................................................................................................................... 8 3 Observations ......................................................................................................................... 8 A3. Software .............................................................................................................................. 11 A4. Source code ....................................................................................................................... -
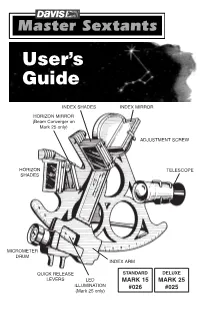
Sextant User's Guide
Master Sextant User’s Guide 00026.710, Rev. F October 2008 Total pages 24 Trim to 5.5 x 8.5" Black ink only User’s Guide INDEX SHADES INDEX MIRROR HORIZON MIRROR (Beam Converger on Mark 25 only) ADJUSTMENT SCREW HORIZON TELESCOPE SHADES MICROMETER DRUM INDEX ARM QUICK RELEASE STANDARD DELUXE LEVERS LED MARK 15 MARK 25 ILLUMINATION #026 #025 (Mark 25 only) Page 1 (front cover) Replacement Parts Contact your local dealer or Davis Instruments to order replacement parts or factory overhaul. Mark 25 Sextant, product #025 R014A Sextant case R014B Foam set for case R025A Index shade assembly (4 shades) R025B Sun shade assembly (3 shades) R025C 3× telescope R026J Extra copy of these instructions R025F Beam converger with index mirror, springs, screws, nuts R025G Sight tube R026D Vinyl eye cup R026G 8 springs, 3 screws, 4 nuts R025X Overhaul Mark 15 Sextant, product #026 R014A Sextant case R014B Foam set for case R026A Index shade assembly (4 shades) R026B Sun shade assembly (3 shades) R026C 3× telescope R026D Vinyl eye cup R026G 8 springs, 3 screws, 4 nuts R026H Index and horizon mirror with springs, screws, nuts R026J Extra copy of these instructions R026X Overhaul R026Y Sight tube Master Sextants User’s Guide Products #025, #026 © 2008 Davis Instruments Corp. All rights reserved. 00026.710, Rev. F October 2008 USING YOUR DAVIS SEXTANT This booklet gives the following information about your new Davis Sextant: • Operating the sextant • Finding the altitude of the sun using the sextant • Using sextant readings to calculate location • Other uses for the sextant To get the most benefit from your sextant, we suggest you familiarize yourself with the meridian transit method of navigation. -

Sight Reduction for Navigation
SIGHT REDUCTION FOR NAVIGATION Table of Contents I. Time A. Time Itself 2 B. Time and the Noon Sight 1. Latitude by Mer Pass at Lan 3 2. Longitude by Mer Pass, Sunrise or Sunset 3 II. The Navigational Triangle A. Navigational Triangle 4 B. Oblique Spherical Triangle 5 C. Right Spherical Triangles 8 1. Ageton H.O. 211 8 2. Dreisonstok H.O. 208 9 D. Comparison of Ageton, Dreisonstok, and H.O. 9 10 1. Definitions 10 2. Mathematics 11 III. The Great Circle Track 13 IV. Useful References 14 SIGHT REDUCTION FOR NAVIGATION I. TIME A. TIME ITSELF Time is longitude. Geocentrically speaking the sun goes round the earth 360 degrees every twenty four hours, more or less. That is, spherically: ANGLE TIME DISTANCE DISTANCE Equator 30 North Lat 360° equals 24 hours equals 21,600 NM 14,400 NM 15° equals 1 hour equals 900 600 1° equals 4 minutes equals 60 40 15N equals 1 minute equals 15 10 1N equals 4 seconds equals 1 1,235 m 15O equals 1 second equals 1,235 m 309 m Since Greenwich is 0° longitude (symbol lambda 8) and Dallas is 8 96° 48N W, Dallas is 6 hours, 27 minutes, 12 seconds west of Greenwich in time. This is exact time from place to place so noon local mean time would be 18h27m12s GMT.. Once upon a time there was much ado about time zones, i.e, Central or Pacific, and about watch or chronometer error, but now since everyone has reference to GMT by his computer, watch or radio, GMT (recently officially called UTC) is the gold standard. -

Bowditch on Cel
These are Chapters from Bowditch’s American Practical Navigator click a link to go to that chapter CELESTIAL NAVIGATION CHAPTER 15. NAVIGATIONAL ASTRONOMY 225 CHAPTER 16. INSTRUMENTS FOR CELESTIAL NAVIGATION 273 CHAPTER 17. AZIMUTHS AND AMPLITUDES 283 CHAPTER 18. TIME 287 CHAPTER 19. THE ALMANACS 299 CHAPTER 20. SIGHT REDUCTION 307 School of Navigation www.starpath.com Starpath Electronic Bowditch CHAPTER 15 NAVIGATIONAL ASTRONOMY PRELIMINARY CONSIDERATIONS 1500. Definition ing principally with celestial coordinates, time, and the apparent motions of celestial bodies, is the branch of as- Astronomy predicts the future positions and motions tronomy most important to the navigator. The symbols of celestial bodies and seeks to understand and explain commonly recognized in navigational astronomy are their physical properties. Navigational astronomy, deal- given in Table 1500. Table 1500. Astronomical symbols. 225 226 NAVIGATIONAL ASTRONOMY 1501. The Celestial Sphere server at some distant point in space. When discussing the rising or setting of a body on a local horizon, we must locate Looking at the sky on a dark night, imagine that celes- the observer at a particular point on the earth because the tial bodies are located on the inner surface of a vast, earth- setting sun for one observer may be the rising sun for centered sphere. This model is useful since we are only in- another. terested in the relative positions and motions of celestial Motion on the celestial sphere results from the motions bodies on this imaginary surface. Understanding the con- in space of both the celestial body and the earth. Without cept of the celestial sphere is most important when special instruments, motions toward and away from the discussing sight reduction in Chapter 20. -

Combined Method of Sight Reduction
the International Journal Volume 15 on Marine Navigation Number 2 http://www.transnav.eu and Safety of Sea Transportation June 2021 DOI: 10.12716/1001.15.02.16 Combined Method Of Sight Reduction A. Buslă Constanta Maritime University, Constanta, Romania ABSTRACT: As ships and maritime transport have evolved, knowledge of navigation methods has also evolved, reaching today modern means that require less of the skills and time of navigators to determine the position of the ship on sees and oceans. However, the IMO resolutions maintain the obligation for seafarers to know the procedure for deter-mining the position of the ship based on the use of astronomical position lines, a process known simply as the "Intercept Method". As is well known, the classical "Intercept Method" involves a graphical stage aimed to determine the geographical coordinate of Fix position. This paper presents a combined method which eliminates the graphical construction which may involve plotting errors. The method introduces mathematical computation of fix geographical coordinates. 1 INTRODUCTION the error induced by DRP. This means that we introduce this error for twice. From the time of French Admiral Marcq St. Hilaire The method proposed by this paper reduces the sailors inherited and successfully used a method of errors by half given that the second LOP is calculated determining the position of the ship, a method that starting from a point located on the first LOP which bears her name and is known in the Anglo-Saxon means that it can be assimilated to a fixed position. language as the "Intercept Method". This point is the intersection point of the intercept The classical method, as it exists today, consists in with the azimuth. -

Longitude by the Method of Lunar Distance
Longitude by the Method of Lunar Distance By Wendel Brunner, PhD, MD, Mar 21, 2005 Finding longitude at sea without a chronometer by the method of lunar distance is the most difficult and complex aspect of celestial navigation. It is unlikely, in the 21st century, that you would ever have to rely on this method to find your way home. However, a celestial navigator who theroughly understands “lunars” will also have a sound grasp of all aspects of celestial navigation, and will be comfortable with any celestial navigation problem encountered. And for the celestial enthusiast, there is no greater satisfaction than dispensing with the chronometer and successfully finding a longitude at sea through careful lunar observation. This article provides a concise but complete description of the lunar distance method, suitable for anyone who has basic familiarity with the use of a sextant to find position by celestial navigation. The only tools required are a good quality metal sextant (the plastic ones are not adequate for lunars), the Nautical Almanac, and an inexpensive scientific calculator. The iterative approach to the calculations used here simplifies the observation requirements, and allows concentration on carefully determining the Lunar Distance. The article is divided into separate sections, which cover each aspect of the lunar distance problem: 1. A Short History of Lunars 2. Measuring the Observed Lunar Distance (OLD) 3. Averaging Multiple Observations to Reduce Error 4. A Brief Trigonometric Interlude 5. The Spherical Triangle and Calculator Methods 6. Calculating the OLD for a Known Position and Time 7. Determining GMT and Longitude at Sea from Observation of the Lunar Distance (OLD) 8. -

Chapter 4 Copyright © 1997-2004 Henning Umland All Rights Reserved
Chapter 4 Copyright © 1997-2004 Henning Umland All Rights Reserved Finding One's Position (Sight Reduction) Lines of Position Any geometrical or physical line passing through the observer's (still unknown) position and accessible through measurement or observation is called a line of position or position line , LOP . Examples are circles of equal altitude, meridians, parallels of latitude, bearing lines (compass bearings) of terrestrial objects, coastlines, rivers, roads, railroad tracks, power lines, etc. A single position line indicates an infinite series of possible positions. The observer's actual position is marked by the point of intersection of at least two position lines, regardless of their nature. A position thus found is called fix in navigator's language. The concept of the position line is essential to modern navigation. Sight Reduction Finding a line of position by observation of a celestial object is called sight reduction . Although some background in mathematics is required to comprehend the process completely, knowing the basic concepts and a few equations is sufficient for most practical applications. The geometrical background (law of cosines, navigational triangle) is given in chapter 10 and 11. In the following, we will discuss the semi-graphic methods developed by Sumner and St. Hilaire . Both methods require relatively simple calculations only and enable the navigator to plot lines of position on a navigation chart or plotting sheet (see chapter 13). Knowing altitude and GP of a body, we also know the radius of the corresponding circle of equal altitude (our line of position) and the location of its center. As mentioned in chapter 1 already, plotting circles of equal altitude on a chart is usually impossible due to their large dimensions and the distortions caused by map projection.