Modeling Human Decision-Making in Spatial and Temporal Systems
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Probable Starters
UTAH JAZZ (35-30) at MEMPHIS GRIZZLIES (18-46) Game #66 • ROAD Game #34 • FedExForum • MEMPHIS March 9, 2018 • 6 p.m. (MT) • TV: AT&T SportsNet RADIO: 1280 AM/97.5 FM DATE OPP. TIME (MT) RECORD/TV 10/18 DEN W, 106-96 1-0 10/20 @MIN L, 97-100 1-1 LAST GAME’S STARTERS (2017-18 averages) 10/21 OKC W, 96-87 2-1 10/24 @LAC L, 84-102 2-2 • Notched first career double-double (11 points, 10/25 @PHX L, 88-97 2-3 career-high 10 assists) at IND on 3/7 10/28 LAL W, 96-81 3-3 PPG • 10.9 10/30 DAL W, 104-89 4-3 2 • Second in the league in three-point 11/1 POR W, 112-103 (OT) 5-3 RPG • 4.1 percentage (.445) 11/3 TOR L, 100-109 5-4 JOE INGLES • Has eight games this season with 5+ 3FG 11/5 @HOU L, 110-137 5-5 11/7 PHI L, 97-104 5-6 F • 6-8 • 226 • Australia APG • 4.3 • Appeared in his 200th straight game on 2/24 11/10 MIA L, 74-84 5-7 vs. DAL 11/11 BKN W, 114-106 6-7 11/13 MIN L, 98-109 6-8 • Has made a three-pointer in consecutive 11/15 @NYK L, 101-106 6-9 PPG • 12.2 games for just the second time in his career 11/17 @BKN L, 107-118 6-10 15 11/18 @ORL W, 125-85 7-10 RPG • 7.4 • Ranks seventh in Jazz history in blocked shots 11/20 @PHI L, 86-107 7-11 DERRICK FAVORS (641) 11/22 CHI W, 110-80 8-11 Jazz are 11-3 when he records a double- 11/25 MIL W, 121-108 9-11 • APG • 1.3 11/28 DEN W, 106-77 10-11 F • 6-10 • 265 • Georgia Tech double 11/30 @LAC W, 126-107 11-11 st 12/1 NOP W, 114-108 12-11 • Posted his 21 double-double of the season 12/4 WAS W, 116-69 13-11 27 PPG • 13.6 (23 points and 14 rebounds) at IND (3/7) 12/5 @OKC L, 94-100 13-12 • Made a career-high 12 free throws and scored 12/7 HOU L, 101-112 13-13 RPG • 10.5 12/9 @MIL L, 100-117 13-14 RUDY GOBERT a season-high 26 points vs. -
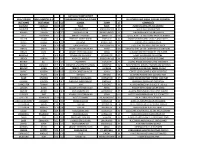
July 10-11 Camp Report (A-B-C Order) Bold Denotes D-1
JULY 10-11 CAMP REPORT (A-B-C ORDER) BOLD DENOTES D-1 UNDERLINED/ITALICS=D-2/NAIA ALL OTHERS HAVE SMALL COLLEGE POTENTIAL LAST NAME FIRST NAME HT CL SCHOOL TOWN ST COMMENTS ASHFORD MARCUS 5'10 12 PARIS PARIS KY POINT CREATES OFF THE DRIBBLE BALDWIN TYLER 6'1 10 GRACE BAPTIST MADISONVILLE KY SOLID ROLE PLAYER TYPE BARNES JOSHUA 5'10 11 SIMON KENTON INDEPENDENCE KY LEAD MAN HANDLES AND PASSES BELL CAMAYAN 5'5 8 MARIETTA MIDDLE MARIETTA GA QUICK, ATHLETIC AND LONG BACKCOURTMAN BILITER EVAN 5'8 7 PINEVILLE INDEPENDENT PINEVILLE KY HARD WORKER WHO SHOOTS AND PASSES BOLES ISAIAH 6'5 12 CAVERNA HORSE CAVE KY STRONG POST BANGS INSIDE BOX LIAM 5'10 10 GRACE BAPTIST MADISONVILLE KY EXCELS AT DISTRIBUTING THE ROCK BRADS JAMES 5'9 12 LEGACY CHRISTIAN ACAD XENIA OH POSSESSES ALL OF THE INGREDIENTS FOR POINT BRADS CLINT LEGACY CHRISTIAN ACAD XENIA OH A LEADER ON BOTH ENDS OF THE FLOOR BRANNEN CJ 6'2 11 COVINGTON CATHOLIC COVINGTON KY LANKY SWINGMAN CAN SCORE BROCK ABRAM 5'7 8 KNOX CO. MIDDLE BARBOURVILLE KY CRAFTY POINT GUARD GOT GAME BROWN ELI 5'7 9 TILGHMAN PADUCAH KY A LONG RANGE SHOOTER WHO STROKES IT BROWN DOMINIC 5'7 9 MEMPHIS UNIVERSITY SCHOOL MEMPHIS TN POINT SHOOTS, DRIVES, FINISHES AND DEFENDS BRYANT VANN 6'7 12 TRINITY CHRISTIAN JACKSON TN MOBILE 3-4 CAN PLAY INSIDE OR OUT BURKE ASHTON 5'10 12 LEGACY CHRISTIAN ACAD XENIA OH CRAFTY LEAD GUARD IS VERY VERSATILE BURNEY KYLAN 6'0 12 ANTIOCH ANTIOCH TN SLASHING PENETRATOR DEFENDS TOO BUSH LINCOLN 6'5 10 FREDERICK DOUGLASS LEXINGTON KY GOOD INSIDE/OUTSIDE THREAT CAN PLAY CALLEBS HAYDEN 5'9 8 PINEVILLE INDEPENDENT PINEVILLE KY POSSESSES EXCELLENT POTENTIAL CARPENTER TOMMY 5'9 8 IHM FLORENCE KY A HARD WORKER WHO GIVES IT HIS ALL CARSON BLAKE LEGACY CHRISTIAN ACAD XENIA OH PASSER WITH GOOD COURT SENSE CARVER ASHER 6'0 9 MUHLENBERG CO. -

Ranking the Greatest NBA Players: an Analytics Analysis
1 Ranking the Greatest NBA Players: An Analytics Analysis An Honors Thesis by Jeremy Mertz Thesis Advisor Dr. Lawrence Judge Ball State University Muncie, Indiana July 2015 Expected Date of Graduation May 2015 1-' ,II L II/du, t,- i II/em' /.. 2 ?t; q ·7t./ 2 (11 S Ranking the Greatest NBA Players: An Analytics Analysis . Iv/If 7 Abstract The purpose of this investigation was to present a statistical model to help rank top National Basketball Association (NBA) players of all time. As the sport of basketball evolves, the debate on who is the greatest player of all-time in the NBA never seems to reach consensus. This ongoing debate can sometimes become emotional and personal, leading to arguments and in extreme cases resulting in violence and subsequent arrest. Creating a statistical model to rank players may also help coaches determine important variables for player development and aid in future approaches to the game via key data-driven performance indicators. However, computing this type of model is extremely difficult due to the many individual player statistics and achievements to consider, as well as the impact of changes to the game over time on individual player performance analysis. This study used linear regression to create an accurate model for the top 150 player rankings. The variables computed included: points per game, rebounds per game, assists per game, win shares per 48 minutes, and number ofNBA championships won. The results revealed that points per game, rebounds per game, assists per game, and NBA championships were all necessary for an accurate model and win shares per 48 minutes were not significant. -

2017 BOYS Gymrat CHALLENGE POST-EVENT REPORT
2017 BOYS GymRat CHALLENGE POST-EVENT REPORT 17U Age Division Report 16U Age Division Report 15U Age Division Report 14U Age Division Report 13U Age Division Report 12U Age Division Report By STEVE AMEDIO GymRat CHALLENGE Director of Communications [email protected] SARATOGA SPRINGS, NY-If one thing has become certain over the two decades of the GymRat CHALLENGE, it's that it takes a lot more than just having a team of individual standouts to win a championship at the storied event. It does take a combination of will and skill, but more importantly is team play and defense, two aspects of the game not always associated with the sport on the AAU level. But, that so-called dirty work on the defensive end, along with an often-difficult to accomplish team chemistry on offense once again proved to be the winning formula for most of the teams in the 20th edition of the prestigious event held in New York's Capital Region over Memorial Day Weekend. No one said it better that Pat McGlynn, coach of the Gold Bracket title at the 17-under age division. "We've got 10 hillbillies who all know what counts in events like this," said McGlynn. "These kids all came here just to play basketball." PAGE | 1 And so they did, and they did it well. The York Ballers were particularly proficient on the defensive end, limiting its three opponents to a tournament-low 70 total points in their three pool-round games and not many more in the championship round. Platinum Bracket champion at the 17-under division, the New York Havoc squad, similarly played a team-first style to find their stride and capture a title. -

Northeast Recruiting Report Issue VI, Volume XXVI – July Preview
Northeast Recruiting Report Issue VI, Volume XXVI – July Preview Albany City Rocks Program Director: Jim Hart, 518-527-4565, [email protected] July 13th – 15th: BasketBull National Invitational – Springfield, MA July 25th – 30th: AAU Junior Nationals – Orlando, FL Chinoso Obokoh, 6’9”, F/C, Bishop Kearney (NY), 2013, HM/MM Long and cut; high level athlete, shot-blocker and defender Javion Onegyemi, 6’8”, PF, Troy (NY), 2013, HM/MM Strong & versatile forward; can score in multiple ways & create mismatch problems Shadell Millinghaus, 6’2”, G/F, Mack Academy (NC), 2013, MM+/MM Power guard in constant attack mode; drives down hill to rim Tyler McLeod, 6’2”, G/F, Watervliet (NY), 2013, MM/MM- Long athlete makes fair share of shots; must shoot it better Manny Suarez, 6’10”, C, Marist Prep (NJ), 2013, MM- Skilled lefty big man specializes in facing basket from perimeter Denzel Gregg, 6’6”, PF, St. Thomas More (CT), 2013, MM- Undersized 4-man; very high level athlete; young for grade Jordan Gleason, 6’2”, SG, Watervliet (NY), 2013, MM/LM Athletic scoring guard has a shot-making component to his game as well Jayde Dawson, 6’2”, SG, Brooks (MA), 2013, LM+ Well built combo; very good on the ball defender. Antwoine Anderson, 6’1”, G, Bishop Kearney (NY), 2013, LM Attacking lefty guard makes things happen on both ends & brings energy Jack Morrow, 6’3”, SF, Albany Academy (NY), 2013, LM-/D3+ Spot-up shot-maker provides spacing & fundamental role player; limited athlete BABC Head Coach: Leo Papile, 617-877-4920 July 18th – 22nd: Nike Peach Jam – North Augusta, SC July 25th – 30th: AAU Junior Nationals – Orlando, FL Jaylen Brantley, 5’10”, PG, Wilbraham & Monson (MA), 2013, HM- Shot-making point guard has proven ability to run show at highest levels of competition Goodluck Okonoboh, 6’9”, C/F, Tilton School (NH), 2013, HM- High level athlete and one of best shot-blockers in the northeast Rene Castro, 6’1”, G, Worcester Academy (MA), 2013, HM-/MM+ Volume scorer can put points on the board but needs ball in his hands Andrew Chrabascz, 6’7”, PF, Cushing Academy (MA), 2013, MM+ Mr. -

Leonard Hamilton)
JONATHAN ISAAC FORWARD/6-10/210 NAPLES, FLORIDA IMG ACADEMY (JOHN MAHONEY) FLORIDA STATE UNIVERSITY (LEONARD HAMILTON) “Jonathan Isaac is the type of versatile combo forward every coach in the country would like to have. Isaac is 6-9 but he has always been groomed as a perimeter player. He has a nice face-up jump shot with range out to the 3-point line. He has a thin frame and should be considered a stretch four in college. His combination of height and skill makes his a mismatch nightmare from the moment he steps onto a college court,” says Ricky O’Donnell of SB Nation… ON ISAAC: The crown jewel of Florida State’s 2016 recruiting class…an ultra-talented forward who is regarded as one of the top recruits in the history of the Florida State program…a forward who developed his tremendous skills as a guard before growing an incredible seven inches during his high school career…likes to play on the perimeter…gets off of the floor well with exceptional quickness…a high release point and a smooth follow through...strong footwork and a solid first step…his combination of size, fluidity and polished offensive skills are rare for a 6-10 player…ranked as the No. 9 overall player in the nation by ESPN.com…ranked No. 9 among all prep players by Scout.com…the No. 3 overall ranked power forward in the Class of 2016 and the No. 1 ranked small forward in the south and the No. 1 ranked small forward in Florida by Scout.com…the No. -

The End. Oct8
THE END. OCT8 The 8th Grade Division featured SO MANY of the top players in the class! The division featured such nationally ranked and recognized players like Jayden Forrest, Lemarcus “Snoody” Wilkinson, Josh Holloway, EJ Smith, Jamarion “Woodie” Harvey, and Regale Moore. The season was full of excitement. There were dozens of twenty points performances, countless highlight plays, and almost every game was a close one. We got a chance to see several of the top players in the class go head up; EJ vs. Josh, Matthew vs. Rashad, and Snoody vs. Woodie. We also got a chance to see some kids really breakout and establish themselves amongst the top ranks. Marcus Crawford, Fred Deere, and Anthony Medlock all played their ways into the conversation. There were few more kids that turned heads. Aidan Moskovitz and Kameron Temple were a couple of those kids. FIRST TEAM ALL-FIRST48 Player’s Name Position Team Ernest “EJ” Smith G Crockett/ Smith Lemarcus “Snoody” Wilkinson G James Jamarion “Woodie” Harvey G Moore Anthony Medlock F Holloway/Morris Fred “Mane Mane” Deere F Williams SECOND TEAM ALL-FIRST48 Player’s Name Position Team Regale Moore G Moore Ryaan Forrest G Grady *Josh Holloway G Holloway/Morris *Andre Watson G Williams Langston Rogers F Crockett/Smith Javar Daniel F Grady *Tie FIRST48 CHAMPIONS. FIRST48 RUNNER-UPS. FIRST48 MVP & MR.FIRST48. Pictured Center: Ernest “EJ” Smith The “FIRST48 MVP” is given to the player who averages the most points on the Championship Team. “Mr.FIRST48” is the player who averages the most points for the entire league. -

Measuring Spatial Allocative Efficiency in Basketball
Measuring Spatial Allocative Efficiency in Basketball Nathan Sandholtz, Jacob Mortensen, and Luke Bornn Simon Fraser University August 4, 2020 Abstract Every shot in basketball has an opportunity cost; one player's shot eliminates all potential opportunities from their teammates for that play. For this reason, player-shot efficiency should ultimately be considered relative to the lineup. This aspect of efficiency—the optimal way to allocate shots within a lineup|is the focus of our paper. Allocative efficiency should be considered in a spatial context since the distribution of shot attempts within a lineup is highly dependent on court location. We propose a new metric for spatial allocative efficiency by comparing a player's field goal percentage (FG%) to their field goal attempt (FGA) rate in context of both their four teammates on the court and the spatial distribution of their shots. Leveraging publicly available data provided by the National Basketball Association (NBA), we estimate player FG% at every location in the offensive half court using a Bayesian hierarchical model. Then, by ordering a lineup's estimated FG%s and pairing these rankings with the lineup's empirical FGA rate rankings, we detect areas where the lineup exhibits inefficient shot allocation. Lastly, we analyze the impact that sub-optimal shot allocation has on a team's overall offensive potential, demonstrating that inefficient shot allocation correlates with reduced scoring. Keywords: Bayesian hierarchical model, spatial data, ranking, ordering, basketball *The first and second authors contributed equally to this work. 1 Introduction arXiv:1912.05129v2 [stat.AP] 1 Aug 2020 From 2017 to 2019, the Oklahoma City Thunder faced four elimination games across three playoff series. -

Basketball Game
2012 E.C (2019\2020) ACADEMIC YEAR THIRD QUARTER H.P.E HANDOUT FOR GRADE 11 Name:_____________________________________ section:________ Basketball Game Basketball rules have some differences between the NBA and all other competitions, trying to get some improvement in certain aspects, but the trend is that these differences will fade over time. Basketball Court: The basketball court should be rigid and free of obstructions, with measures 28 meters long by 15 meters wide. The field has several lines and markings that we will now explain one by one as follows: A. Lateral Lines – These lines are on the sides of the court and delimit the same, marking the zone valid to play. B. Limit Line – This line also serves to delimit the field and it is from her that the players replace the ball in play when she left or a basket is made. C. Central Line – The central line is responsible for dividing the field in half and defining which defensive zone and attacker belongs to which team. D. Line 3 points – The pitches that are made behind this line are worth 3 points to enter. The line is 6,75 meters from the basket. E. Free Throw Line – It is from this line that the players who will make a free throw the ball. At launch, the player cannot step on the line or overtake it before the ball touches the rim. F. Free Throw Circle – The free-throw circles have a diameter of 3.65 meters. During the free-throw throw, the shooter must remain within the free-throw circle. -

Using Topological Clustering to Identify Emerging Positions and Strategies in NCAA Men’S Basketball
University of Tennessee, Knoxville TRACE: Tennessee Research and Creative Exchange Masters Theses Graduate School 5-2018 Using Topological Clustering to Identify Emerging Positions and Strategies in NCAA Men’s Basketball Nathan Joel Diambra University of Tennessee, [email protected] Follow this and additional works at: https://trace.tennessee.edu/utk_gradthes Recommended Citation Diambra, Nathan Joel, "Using Topological Clustering to Identify Emerging Positions and Strategies in NCAA Men’s Basketball. " Master's Thesis, University of Tennessee, 2018. https://trace.tennessee.edu/utk_gradthes/5084 This Thesis is brought to you for free and open access by the Graduate School at TRACE: Tennessee Research and Creative Exchange. It has been accepted for inclusion in Masters Theses by an authorized administrator of TRACE: Tennessee Research and Creative Exchange. For more information, please contact [email protected]. To the Graduate Council: I am submitting herewith a thesis written by Nathan Joel Diambra entitled "Using Topological Clustering to Identify Emerging Positions and Strategies in NCAA Men’s Basketball." I have examined the final electronic copy of this thesis for form and content and recommend that it be accepted in partial fulfillment of the equirr ements for the degree of Master of Science, with a major in Recreation and Sport Management. Jeffrey A. Graham, Major Professor We have read this thesis and recommend its acceptance: Adam Love, Sylvia A. Trendafilova, Vasileios Maroulas Accepted for the Council: Dixie L. Thompson Vice Provost and Dean of the Graduate School (Original signatures are on file with official studentecor r ds.) Using Topological Clustering to Identify Emerging Positions and Strategies in NCAA Men’s Basketball A Thesis Presented for the Master of Science Degree The University of Tennessee, Knoxville Nathan Joel Diambra May 2018 Copyright © 2018 by Nathan Joel Diambra All rights reserved. -

Singles Complex Petition for Public Address System
We’re in love with KFC’s new Kherat receives national advertising campaign. recognition. Page B3 Page A8 Vol. 124 | No. 8 | November 1, 2019 The Scout @bradley_scout Lockdown Singles Complex BASKETBALL PREVIEW incident petition for public It’s that time of year again. With both upgraded to Bradley basketball teams set to begin aggravated their season this week, check out The address system Scout’s annual basketball preview assault on pages A9 through A12. BY ANGELINE SCHMELZER information of the tornado warnings BY COLE BREDAHL Assistant News Editor on Sept. 27 through text messaging Editor-at-Large to resident advisers of the Singles Many residence halls on campus Complex. The incident involving a Bradley have the mass notification internal After bringing his concerns to student that resulted in a campus public address system, but the Singles superiors in Residential Living, lockdown early Saturday morning Complex do not. Endres said there has not been any has been reclassified as an aggravated A Bradley student started a action. assault. After the Bradley University petition after the Oct. 26 campus “The fact that I have brought Police Department conducted a lockdown to install the internal it up and it’s just been dismissed more detailed interview, the alleged public address system in the Singles as not important, to be told that victim recalled the suspect pointed a Complex. I’m overreacting about not having a handgun at him. “I remember I was torn between, safety system, I think that also drew “The victim was driving down ‘Do I go up to my room and take a line for me,” Endres said. -

2020-21 Duke Basketball
2020-21 DUKE BASKETBALL CLIPS FILE » 2020-21 DUKE BASKETBALL | CLIPS FILE If Duke is to make a run to NCAA tourney, Mark Williams just showed how to do it By Luke DeCock, Raleigh News & Observer (March 10, 2021) GREENSBORO - At this point, after a season of false dawns, far be it from anyone to claim, presume, surmise or otherwise deduce that Duke has turned some kind of a corner. One can only fall into that trap so many times. But, just for sake of argument, if Duke were going to pull off the improbable five-in- five at the ACC tournament, or at the least win enough to actually make a legitimate case for the NCAA tournament, the way Duke has played so far in Greensboro is how Duke would have to play to make it happen. “So far” is doing a lot of heavy lifting there, with Florida State looming in Thursday’s quarterfinals, but Tuesday night’s win over Boston College and Wednesday’s 70-56 win over Louisville had a lot in common, starting with the continuing emergence of freshman big man Mark Williams as an unstoppable force and on down the line. With Matthew Hurt making some unlikely shots from uncertain positions and the freshman backcourt of DJ Steward and Jeremy Roach showing considerable defensive improvement, the things Duke needed to fall into place are falling into place. There was a lot of back and forth in Wednesday’s first half — a 12-0 Duke run followed by an 16-0 Louisville run followed by a 12-0 Duke run that spilled into the second half — but the Blue Devils took firm control after that.