DOCSLIB.ORG

Neutrinos from Supernovae

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Neutrinos from Supernovae Proc Indian Natn Sci Acad, 70, A No. 1, January 2004, pp. 123–133 c Printed in India. Neutrinos from Supernovae a † SANDHYA CHOUBEY ¡ AND KAMALES KAR ¡ Department of Physics and Astronomy, University of Southampton, Highfield, Southampton S017 1BJ (UK) †Theory Group, Saha Institute of Nuclear Physics, Kolkata 700 064 (India) (Received 10 January 2003; Accepted 17 July 2003) In this review, the effect of flavor oscillations on the neutrinos released during supernova explosion after core collapse is described. In some scenarios there is a large enhancement of the number of events compared to the no oscillation case. Various other features associated with supernova neutrinos are also discussed. Key Words: Core Collapse Supernova; Neutrino Mass and Mixing; Neutrino Detection 1 Introduction Sudbury Neutrino Observatory (SNO) through elec- tron scattering and charged/neutral current dissocia- February 23, 1987 saw the birth of a new era in tion of heavy water respectively. The recent results an- astrophysics-extra-solar system neutrino astronomy. nounced by the KamLAND reactor experiment gives The supernova explosion in the Large Magellanic for the first time conclusive evidence for neutrino os- Cloud (LMC) at a distance of about 50 kpc was not cillation using a terrestrial neutrino source and con- only the closest visual supernova since Kepler but was firms the Large Mixing Angle (LMA) solution to the also the source of neutrinos detected at the terrestrial solar neutrino problem. Thus the present day interest detectors of Kamiokande (KII) and IMB giving rise to in supernova neutrinos lies around the question: if you 11 and 8 events respectively. have a galactic supernova event today what would be The next few years saw great excitement in this the number of events and their time and energy dis- field. Astrophysics interacted with particle physics tributions in the large number of neutrino detectors intimately. From the number and the energy dis- in operation. The other related question is whether tribution of the observed neutrinos one tried to ex- one can get a signature of neutrino oscillation mecha- tract information about the stellar core and check nism from the observed data and also how other neu- them with model predictions. On the other hand trino properties get constrained. Information about the these neutrinos also gave particle physics constraints mechanisms of the supernova explosion is also an area on neutrino properties. In the last few years inter- of huge interest. est in this area got rejuvenated by the finding that In this review we survey some of these issues. neutrinos do have non-zero mass and the flavors do In section 2 we give a brief overview of the physics mix when they travel. This conclusion was reached of type II supernovae and the emission of neutrinos through the analysis of the atmospheric neutrinos de- from them. Section 3 introduces the subject of neu- tected at the Superkamioka (SK) along with their trino oscillation and the impact of vacuum and matter zenith angle dependence and the observation of the enhanced oscillation on the supernova neutrinos from deficit of detected solar neutrinos by the Chlorine the core. Section 4 describes the expected number of and Gallium radiochemical detectors and at SK and events in the terrestrial detectors for the different mass and mixing scenarios. Finally section 5 briefly states a Now at INFN Sezione di Trieste and Scuola Internazionale the other connected issues of supernova neutrino de- Superiore di Studi Avazanti, I-34014, Trieste, Italy. tection. 124 SANDHYA CHOUBEY AND KAMALES KAR 2 Type II Supernovae and Neutrino Emission and so the νe “neutrinosphere” has the largest radius and smallest temperature. In this article we shall as- Stars of masses larger than 8M ¢ after burning for sume that the three types of neutrino gas have Fermi- millions of years collapse when the nuclear reac- Dirac distributions with temperatures 11, 16 and 25 tions in the core stop with matter consisting mostly MeV for νe, ν¯e and νx respectively. of 56Fe like nuclei. This collapse proceeds very fast An important role played by neutrinos in type (timescale of the order of tens of milliseconds) and II supernovae is in the process of “delayed neutrino stops in the central region when its density goes be- heating”5 . In almost all simulations for large mass yond the nuclear matter density with a strong shock stars one sees that the shock wave moving outward starting to travel outward1. This shock wave, even- fast loses energy in dissociating the nuclei in the over- tually hitting the outer mantle in a few seconds and lying matter and soon becomes an accretion shock. supplying the explosion energy of a few times 1051 This shock gets revitalized over the much longer ergs, is believed to be the cause of type II supernova timescale of seconds through the absorption of a small explosion. During this process, the binding energy re- fraction of the thermal neutrinos that radiate out with leased comes out almost completely as neutrinos and each neutrino depositing energy of the order of 10 antineutrinos of three different flavors (e, µ and τ) in MeV. Large convection in the central regions also the “cooling phase” with the total energy release of helps this process. the order of 1053 ergs. Let us discuss the emission of the neutrinos in some more detail. Firstly during 3 The Neutrino Oscillation Probabilities the early stage of the collapse (densities less than 1012 g/cc) neutrinos are produced through neutronization να The flavor eigenstate created inside the super- ν nova can be expressed as a linear superposition of the £¥¤§¦ ¨ © ¦ ¤ ¨ ©¤ e N Z N 1 Z 1 e (1) ν ν α ∑ mass eigenstates such that i Uαi i , where U is the unitary mixing matrix and the sum is over N ν α ν neutrino states. After time t, the initial evolves £¤ ¤ e p n e (2) iEit ¦ © ν ν α ∑ £ to t i e Uαi i where Ei is the energy of th where only ν (not ν¯) are produced. At lower densi- the i mass eigenstate. Then the probability of find- e e ν ν ties these neutrinos have mean free path much larger ing a flavor β in the original α beam after traveling than the core radius and hence escape. But the to- a distance L in vacuum is given by tal energy of these neutronization neutrinos is much δ Pαβ αβ smaller than that in the cooling phase. Even then it ∆ 2 is possible to detect them for nearby galactic super- 2 mi jL ¨ 2 4 ∑ UαiUβiUα jUβ j sin 1 27 (3) novae at distances within 1 kpc . These neutrinos can E j i give information about the temperature and composi- ∆ 2 2 2 tion of the core. where mi j mi m j is the mass squared difference. The main neutrino emission is during the cooling Over the last few years the idea that neutrinos are phase where the thermal ν/ν¯ are produced through not massless but have small masses has become estab- pair production and other processes3 . Out of these lished as a result of Super-Kamiokande (SK) and SNO νµ , ντ , ν¯µ and ν¯τ , called collectively as νx, interact which have firm evidence for atmospheric and solar 6 11 with matter only through neutral current whereas νe neutrino oscillations . The SK atmospheric neu- 2 3 2 ν ∆ and ¯ have both charged current and neutral current trino data demand m 3 10 £ eV and almost e 32 interaction with matter. As the matter is neutron-rich maximal mixing (sin2 2θ 1) 6 while the global so- 23 ν ν ∆ 2 the ’s interact more with matter than the ¯’s. These lar neutrino data is best explained if m 6 1 e e 21 5 2 2 θ 10, 12 £ neutrinos deep inside the core are in equilibrium with 10 eV with large mixing angles (tan 0 41) . the ambient matter and their energy distributions are Very recently the KamLAND reactor antineutrino dis- close to Fermi-Dirac as seen through simulations and appearance experiment 13 provided conclusive con- through the analysis of 1987A neutrinos4 . As the stel- firmation of the LMA solution to the solar neutrino lar core has a strong density gradient, electron type problem, with mass and mixing parameters absolutely neutrinos can stay in equilibrium upto larger radius consistent with the solar neutrino results. The global NEUTRINOS FROM SUPERNOVAE 125 14 n ' ρ & analysis of the solar and the KamLAND data gives very well approximated by a power law r Cr " ∆ 2 5 2 2 θ 18 ! " m 7 17 10 eV and tan 0 44. The with n 3 in the core . 2 CHOOZ reactor experiment restricts sin θ 0 1 for Neutrino oscillation probabilities may also be sig- 13 # ∆ 2 $ 3 215 m 10 " eV . The only other positive signal for nificantly affected inside Earth as the neutrinos tra- neutrino oscillations comes from the accelerator ex- verse the Earth matter19. Thus the neutrino oscillation periment LSND which requires ∆m2 % eV2 and mix- probability is given by 2 θ % 3 ing angle small (sin 2 10 " ). To include LSND N in the framework of oscillation one needs to extend m P ∑ Pα P + β (6) the number of neutrino generations to four, or in other αβ i i , i * 1 words, include a sterile neutrino. However with the latest SNO data on solar neutrinos and the final data where from SK on atmospheric neutrinos, both the “2+2” N 2 2 m m m and “3+1” 4-generation scenarios fail to explain the Pα ∑ Uα ν ν (7) 1 i j i 0 j - - - - global neutrino data.
Load more

Recommended publications
  • On the Road to the Solution of the Solar Neutrino Problem RECEIVED
    LBNL-39099 UC-414 C6AiF- ERNEST DRLANDD LAWRENCE BERKELEY NATIONAL LABORATORY I BERKELEY LAB| On the Road to the Solution of the Solar Neutrino Problem E.B. Norman Nuclear Science Division RECEIVED August 1995 SEP 20 1996 Presented at the OSTI Fourth International Workshop on Relativistic Aspects of Nuclear Physics, Rio de Janeiro, Brazil, August28-30,1995, and to be published in the Proceedings DISTRIBUTION OF THIS DOCUMENT IS UNUMITiD DISCLAIMER This document was prepared as an account of work sponsored by the United States Government. While this document is believed to contain correct information, neither the United States Government nor any agency thereof, nor The Regents of the University of California, nor any of their employees, makes any warranty, express or implied, or assumes any legal responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process, or service by its trade name, trademark, manufacturer, or otherwise, does not necessarily constitute or imply its endorsement, recommendation, or favoring by the United States Government or any agency thereof, or The Regents of the University of California. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof, or The Regents of the University of California. Ernest Orlando Lawrence Berkeley National Laboratory is an equal opportunity employer. DISCLAIMER Portions of this document may be illegible in electronic image products. Images are produced from the best available original document.
    [Show full text]
  • Supernova Neutrinos in the Proto-Neutron Star Cooling Phase and Nuclear Matter
    TAUP 2019 IOP Publishing Journal of Physics: Conference Series 1468 (2020) 012089 doi:10.1088/1742-6596/1468/1/012089 Supernova neutrinos in the proto-neutron star cooling phase and nuclear matter Ken’ichiro Nakazato1 and Hideyuki Suzuki2 1 Faculty of Arts and Science, Kyushu University, 744 Motooka, Nishi-ku, Fukuoka 819-0395, Japan 2 Faculty of Science & Technology, Tokyo University of Science, 2641 Yamazaki, Noda, Chiba 278-8510, Japan E-mail: [email protected] Abstract. A proto-neutron star (PNS) is a newly formed compact object in a core collapse supernova. Using a series of phenomenological equations of state (EOS), we have systematically investigated the neutrino emission from the cooling phase of a PNS. The numerical code utilized in this study follows a quasi-static evolution of a PNS solving the general-relativistic stellar structure with neutrino diffusion. As a result, the cooling timescale evaluated from the neutrino light curve is found to be long for the EOS models with small neutron star radius and large effective mass of nucleons. It implies that extracting properties of a PNS (such as mass and radius) and the nuclear EOS is possible by a future supernova neutrino observation. 1. Introduction Core collapse supernovae, which are the spectacular death of massive stars, emit an enormous amount of neutrinos. In the case of SN1987A, a few tens of events were actually detected [1, 2, 3] and contributed to confirm the standard scenario for supernova neutrino emission. Although the neutron star formed in SN1987A has not yet been observed, its mass estimations had been attempted by using the neutrino event number [4, 5].
    [Show full text]
  • Neutrinos from Core-Collapse Supernovae and Binary Neutron Star Mergers
    Neutrinos from core-collapse supernovae and binary neutron star mergers Maria Cristina Volpe Astroparticules et Cosmologie (APC), Paris, France Sun core-collapse Supernovae McLaughlin Perego et al, 2014 accretion disks around black holes or neutron star mergers remnants Solar neutrino observations Vacuum averaged oscillations pep MSW solution 7Be 8B ν Survival Probability e Borexino, Nature 512 (2014) ν Neutrino Energy (MeV) Vacuum-averaged oscillations versus MSW suppression of high energy 8B neutrinos. Energy production of low mass main sequence stars confirmed — pp reaction chain. Future measurement of CNO neutrinos - main energy production in massive main sequence stars. The Mikheev-Smirnov-Wolfenstein effect Neutrinos interact with matter and undergo resonant adiabatic flavor conversion. Wolfenstein PRD (1978) Mikheev, Smirnov(1985) hmat = p2GF ⇢e mean-field approximation matter basis flavour basis ~ ν2 =νe ν , ν ν ν ~ ν2 µ τ e 2 ~ ν 1 =νµ ν~ 1 Effective mass Effective vacuum ν1 MSW resonance DENSITY 2 ∆m˜ /4E i✓˙M h⌫ = − − neutrino hamiltonian in the matter basis i✓˙ ∆m˜ 2/4E ✓ M ◆ ✓˙M Resonance condition : Adiabaticity : γ = | 2 | << 1 h h 0 ∆m˜ /4E ⌫,11 − ⌫,22 ⇡ Also in supernovae, in accretion disks around compact objects, in the Earth and in the Early Universe (BBN epoch) Heavy elements nucleosynthesis Two main mechanisms at the origin of elements heavier than iron : s-process (s-slow) and r-process (r-rapid). Double peak structures at the first A=90, the second A=130 and third A=190 peaks due to both the s-process and the r-process. The r-process sites : a longstanding question The r-process : neutron-capture is fast compared to half-lives of neutron-rich unstable nuclei.
    [Show full text]
  • Resolving the Solar Neutrino Problem
    FEATURES Resolving the solar neutrino problem: Evidence for massive neutrinos in the Sudbury Neutrino Observatory Karsten M. Heeger for the SNO collaboration ............................................................................................................................................................................................................................................................ The solar neutrino problem are not features of the Standard Model of particle physics. In or more than 30 years, experiments have detected neutrinos quantum mechanics, an initially pure flavor (e.g. electron) can Pproduced in the thermonuclear fusion reactions which power change as neutrinos propagate because the mass components that the Sun. These reactions fuse protons into helium and release neu­ made up that pure flavor get out of phase. The probability for trinos with an energy of up to 15 MeY. Data from these solar neutrino oscillations to occurmayeven be enhanced in the Sun in neutrino experiments were found to be incompatible with the an energy-dependent and resonant manner as neutrinos emerge predictions of solar models. More precisely, the flux ofneutrinos from the dense core of the Sun. This effect of matter-enhanced detected on Earthwas less than expected, and the relative intensi­ neutrino oscillations was suggested by Mikheyev, Smirnov, and ties ofthe sources ofneutrinos in the sun was incompatible with Wolfenstein (MSW) and is one of the most promising explana­ those predicted bysolar models. By the mid-1990's the data
    [Show full text]
  • An Introduction to Solar Neutrino Research
    AN INTRODUCTION TO SOLAR NEUTRINO RESEARCH John Bahcall Institute for Advanced Study, Princeton, NJ 08540 ABSTRACT In the ¯rst lecture, I describe the conflicts between the combined standard model predictions and the results of solar neutrino experi- ments. Here `combined standard model' means the minimal standard electroweak model plus a standard solar model. First, I show how the comparison between standard model predictions and the observed rates in the four pioneering experiments leads to three di®erent solar neutrino problems. Next, I summarize the stunning agreement be- tween the predictions of standard solar models and helioseismological measurements; this precise agreement suggests that future re¯nements of solar model physics are unlikely to a®ect signi¯cantly the three solar neutrino problems. Then, I describe the important recent analyses in which the neutrino fluxes are treated as free parameters, independent of any constraints from solar models. The disagreement that exists even without using any solar model constraints further reinforces the view that new physics may be required. The principal conclusion of the ¯rst lecture is that the minimal standard model is not consistent with the experimental results that have been reported for the pioneering solar neutrino experiments. In the second lecture, I discuss the possibilities for detecting \smok- ing gun" indications of departures from minimal standard electroweak theory. Examples of smoking guns are the distortion of the energy spectrum of recoil electrons produced by neutrino interactions, the de- pendence of the observed counting rate on the zenith angle of the sun (or, equivalently, the path through the earth to the detector), the ratio of the flux of neutrinos of all types to the flux of electron neutrinos 1 (neutral current to charged current ratio), and seasonal variations of the event rates (dependence upon the earth-sun distance).
    [Show full text]
  • Gigantic Japanese Detector Seeks Supernova Neutrinos Tracing the History of Exploding Stars Is a Goal of the Revamped Super-Kamiokande
    NEWS IN FOCUS ASAHI SHIMBUN/GETTY Observations by the Super-Kamiokande neutrino detector have forced theorists to amend the standard model of particle physics. PHYSICS Gigantic Japanese detector seeks supernova neutrinos Tracing the history of exploding stars is a goal of the revamped Super-Kamiokande. BY DAVIDE CASTELVECCHI weight. These data will help astronomers to detector much better at distinguishing between better understand the history of supernovae different types, or ‘flavours’, of neutrino, as well leven thousand giant orange eyes in the Universe — but the neutrinos that the as their antiparticles, antineutrinos. confront the lucky few who have explosions emit have been difficult to detect. In 1987, the Kamiokande detector, Super-K’s entered the Super-Kamiokande under- “Every 2–3 seconds, a supernova goes off smaller predecessor, detected the first neutri- Eground neutrino observatory in Japan — by somewhere in the Universe, and it produces nos from a supernova. The dozen neutrinos far the largest neutrino detector of its kind in 1058 neutrinos,” says Masayuki Nakahata, came from Supernova 1987A, which occurred the world. A chance to see these light sensors who heads the Super-K, an international col- in the Large Magellanic Cloud, a small galaxy is rare because they are usually submerged in laboration led by Japan and the United States. that orbits the Milky Way. Head experimenter 50,000 tonnes of purified water. But a major With the upgrade, the detector should be able Masatoshi Koshiba shared the 2002 Nobel revamp of Super-K that was completed in to count a few of these ‘relic’ neutrinos every physics prize partly for that discovery.
    [Show full text]
  • Astroparficle,Physics,, With,Mev,Neutrinos
    University(of(Virginia,(HEP(Seminar,(April(21st(2015( Astropar(cle,physics,, with,MeV,neutrinos, Shunsaku(Horiuchi(( (Center(for(Neutrino(Physics,(Virginia(Tech)( Image(credit:(NASA/ESA( Contents, • IntroducJon:(why(astrophysical(neutrinos(now?( • Topic(1:(Supernova(neutrinos( – GalacJc(events:(rich(physics(and(astronomy( – Detectability(beyond(GalacJc(events( • Topic(2:(Dark(maPer(neutrinos( – Two(searches,(two(constraints( • Summary( UVa,(April(21st(2015( Shunsaku(Horiuchi((Virginia(Tech)( 2( Neutrinos,as,messenger,par(cles Neutrinos(are(great(messenger(parJcles:( • allow(us(to(see(opJcally(thick((to(photons)(regions( • experience(liPle(aPenuaJon(through(cosmic(space( • travel(in(straight(lines( Source Neutrinos gamma(rays( Cosmic(raysCosmic(rays( MagneJc(field UVa,(April(21st(2015 Shunsaku(Horiuchi((Virginia(Tech) 3( Neutrino,detec(on:,Cherenkov,, Use(the(Cherenkov(light(to(reconstruct(the(original(neutrino( ν" IceCube( Eν >(10(GeV( Muon(range(increases( the(effecJve(volume(( lepton( e( Du>a,et,al,,PRD,(2001),, SuperVKamiokande( Eν(>(few(MeV(( Volume(~(50(kton(of(water( Volume(~(1(Gton(of(ice( UVa,(April(21st(2015( Shunsaku(Horiuchi((Virginia(Tech)( 4( Neutrino,sources, RadioacJve(decay( Sun((x1)( Nuclear( Supernova((x1)( reactors( ParJcle( Astrophysical( accelerator( accelerator( Likely' Cosmic(background( Atmospheric( +(others?( UVa,(April(21st(2015(Shunsaku(Horiuchi((IPMU)((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((Shunsaku(Horiuchi((Virginia(Tech)(
    [Show full text]
  • The Solar Neutrino Problem
    The Solar Neutrino Problem Martin Lahrz [email protected] University Umeå Abstract very small. In fact, Pauli himself thought it would not be possible to see it for a long time. Indeed, Since neutrinos are the only known particles being this succeeded for the first time by C. Cowan and able to leave the core of the Sun directly, they were F. Reines[18] in 1956. supposed to approve the Standard Solar Model. How- So far, only the electron neutrino was known but ever, the number of detected neutrinos was only one J. Steinberger, M. Schwartz and L.M. Leder- third of the predicted number.[10] After theoretical com- mann discovered with the muon neutrino a second gen- putations and other experiments had corroborated our eration in 1962[19]. When M.L. Perl found the tauon understanding of the Sun, the question of the miss- in 1975[25], physicists expected also a corresponding ing neutrinos remained as the solar neutrino problem. neutrino generation. In fact, it was verified at the Not until 2001 neutrino oscillations could explain this DONUT experiment in 2000[12] as the latest particle discrepancy[13] and gave in turn new insights about the of the Standard Model being directly observed. neutrinos themselves. 1.2 Properties 1 Neutrinos and their classification Neutrinos are neutral charged elementary particles. As leptons they are fermions and have a spin of 1/2 1.1 From Pauli to the Standard Model which was already postulated by Pauli. As mentioned previously, three different flavors are known: electron A two-body decay produces a discret energy spec- neutrinos, muon neutrinos and tau neutrinos while trum since the conservation of energy and momentum each type has basically an antiparticle.
    [Show full text]
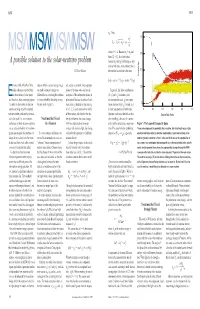
  • MSW-A Possible Solution to the Solar
    MSW MSW mk. Thus, 2 1.0 mk p2 1 m2 } E 5 Ïwwwww < p 1 , k k 2p MSWMSWMSWMSW where k 5 1, 2. Because m Þ m , and 1 2 0.75 hence E1 Þ E2, the relative phase A possible solution to the solar-neutrino problem between |n1l and |n2l will change as |n(t)l evolves with time. At an arbitrary time t, S. Peter Rosen the neutrino has evolved to the state 0.5 Probability 2iE t 2iE t |n(t)l5cos u e 1 |n1l 1 sin u e 2 |n2l ver since 1968, when Ray Davis neutrino within a certain energy range are created as coherent, linear superpo- 0.25 and his colleagues reported their can make a dramatic change to a sitions of the mass states and are the In general, this linear combination Efirst observations of solar neutri- different flavor even though its intrinsic analogues of the independent planes of of |n1l and |n2l is neither a pure os, there have been continuing reports in vacuo probability for doing so may polarization. Because the phase of each electron neutrino state |n l nor a pure e 0 f a deficit in the number of electron be very small (Figure 1). mass state |nkl depends on the mass mk muon neutrino state |nml. Instead, it is eutrinos arriving at Earth compared (k 5 1, 2, 3), each state evolves with a a linear superposition of both states. 0 0.2 0.4 0.6 0.8 1.0 with the number predicted by the stan- different phase, and therefore the rela- Quantum mechanics then tells us that, Distance/Solar Radius ard solar model.
    [Show full text]
  • SNO: Solving the Mystery of the Missing Neutrinos
    SNO Completes Neutrino Data-Taking Nick Jelley (University of Oxford), Alan Poon (Lawerence Berkeley National Lab) The end of an era came on 28 November 2006 when the Sudbury Neutrino Observatory (SNO) finally stopped data-taking after eight exciting years of discoveries. During this time the Observatory saw evidence that neutrinos, produced in the fusion of hydrogen in the solar core, change flavour while passing through the Sun on their way to the Earth. This observation explained the longstanding puzzle as to why previous experiments had seen fewer solar neutrinos than predicted and confirmed that these elusive particles have mass. Solar neutrinos were first detected in Ray Davis’s radiochemical experiment in 1967, for which discovery he shared the 2002 Nobel Prize in Physics. Surprisingly he found only about a third of the number predicted from models of the Sun’s output. This deficit, the so-called Solar Neutrino Problem, was confirmed by Kamiokande-II while other experiments saw related deficits of solar neutrinos. A possible explanation for this deficit, suggested by Gribov and Pontecorvo in 1969, was that some of the electron-type neutrinos, which are produced in the Sun, had ‘oscillated’ into neutrinos that could not be detected in the Davis detector. The oscillation mechanism requires that neutrinos have non-zero mass. The unique advantage, which was pointed out by the late Herb Chen in 1985, of using 8 heavy water (D2O) to detect the neutrinos from B decays in the solar fusion process is that it enables both the number of electron-type and of all types of neutrinos to be measured.
    [Show full text]
  • Kunitomo Sakurai, Solar Neutrino Problems – How They Were Solved Hans J
    obiolog str y & f A O u o l t a r e n a r c u h o J Journal of Astrobiology & Outreach Haubold and Mathai, Astrobiol Outreach 2015, 3:3 DOI: 10.4172/2332-2519.1000132 ISSN: 2332-2519 Book Review Open Access Kunitomo Sakurai, Solar Neutrino Problems – How they were Solved Hans J. Haubold1,2* and Arak M. Mathai1,3 1Centre for Mathematical and Statistical Sciences, Peechi Campus, KFRI, Peechi-680653, Kerala, India 2Office for Outer Space Affairs, United Nations, P.O. Box 500, Vienna International Center, A-1400 Vienna, Austria 3Department of Mathematics and Statistics, McGill University, 805 Sherbrooke Street West, Montreal, Quebec, Canada *Corresponding author: Hans J. Haubold, Office for Outer Space Affairs, United Nations, P.O. Box 500, Vienna International Center, A-1400 Vienna, Austria, Tel: +43-1-260 60 4950; E-mail: [email protected] Rec date: May 28, 2015; Acc date: June 01, 2015; Pub date: June 05, 2015 Copyright: © 2015 Haubold HJ, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited. Book Review and theorized about the Sun can be accounted for in terms of basic physical laws: Newton's laws of gravity and motion, the first two laws The central message of Sakurai’s outstanding book is: The Sun is a of thermodynamics, Einstein's law of the equivalence of mass and surface source of photons. Not in perfect hydrostatic equilibrium the energy, Boyle's law, Charles' law of perfect gases, and Heisenberg's Sun oscillates with periods to be understood similar to seismic waves.
    [Show full text]
  • 21.8 N&V PJ BG.Indd
    NEWS & VIEWS NATURE|Vol 454|21 August 2008 OBITUARY Yoji Totsuka (1942–2008) Leader in the discovery of neutrino oscillations. Yoji Totsuka, a major figure in the world of of the supernova and of the neutrinos particle physics, died on 10 July after a long themselves. battle with cancer. He was a leading light Shortly after the supernova, Koshiba in the thrilling advances in the physics of retired and Totsuka became leader of neutrinos over the past 30 years, and was the Kamiokande project. Two seminal a notably resolute figure in seeing through results from the group were subsequently the rebuilding of the Super-Kamiokande published. The first observed a deficit in neutrino detector after a disastrous accident atmospheric neutrinos that could not be in 2001. explained by systematic experimental errors Born on 6 March 1942, in Fuji, Japan, or uncertainties in the background neutrino Totsuka received his bachelor’s, master’s and flux. Instead, some “as-yet-unaccounted-for PhD degrees from the University of Tokyo. physics”, as the paper put it, might explain His thesis project studied ultra-high-energy the data. The second crucially confirmed the particle interactions, so kick-starting his solar neutrino deficit recorded by Davis. lifelong passion for particle physics. As a In 1991, Totsuka obtained funding for a Totsuka also supervised the successful research associate with the University of successor to Kamiokande. This was Super- Belle B-factory, where particles known as Tokyo, he then travelled to the Deutsches Kamiokande, an underground detector B-mesons were generated to study differences Electron Synchrotron Laboratory in that contained 50,000 tons of water.
    [Show full text]