DOCSLIB.ORG

Graphing and Maximum Minimum

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Graphing and Maximum Minimum Chapter 3 Graphing and - Maximum Minimum Differential calculus provides tests for locating the key features of graphs. Now that we know how to differentiate, we can use this information to assist us in plotting graphs. The signs of the derivative and the second derivative of a function will tell us which way the graph of the function is "leaning" and "bending." Using the derivative to predict the behavior of graphs helps us to find the points where a function takes on its maximum and minimum values. Many interesting word problems requiring the "best" choice of some variable involve searching for such points. In Section 3.1, we study the geometric aspects of continuity. This will provide a useful introduction to graphing. In Section 3.6, we use the ideas of maxima and minima to derive an important theoretical result-the mean value theorem. One consequence of this theorem is a fact which we used in connection with antiderivatives: a function whose derivative is zero must be constant. 3.1 Continuity and the Intermediate Value Theorem If a continuous function on a closed interval has opposite signs at the endpoints, it must be zero at some interior point. In Section 1.2, we defined continuity as follows: "A function f(x) is said to be continuous at x,, if lin,,,o f(x) = f(x,)." A function is said to be continuous on a given interval if it is continuous at every point on that interval. If a function f is continuous on the whole real line, we just say that "f is continuous." An imprecise but useful guide is that a function is continuous when its graph can be drawn "without removing pencil from paper." In Figure 3.1 .l, the curve on the left is continuous at x,, while that on the right is not. Copyright 1985 Springer-Verlag. All rights reserved. "140 Chapter 3 Graphing and Maximum-Minimum Problems a discontinuous curve I 0 I + (right). ," 0 Y X0 I Example 1 Decide where each of the functions whose graphs appear in Fig. 3.1.2 is continuous. Explain your answers. Ftwe 3.1.2. Where are these functions continuous? Solution (a) This function jumps in value at each of the points x, = 0, x, = 2 1, x0 = f2, . , so limx,xo f(x) does not exist at these points and thus f is not continuous there; however, f is continuous on each of the intervals between the jump points. (b) This function jumps in value at x, = - 1 and x, = + 1, and so lim,,,, f(x) and limx,-, f(x) do not exist. Thus f is not continuous at x, = +- 1; it is continuous on each of the intervals (- m, - l), (- 1, l), and (1900). (c) Even though this function has sharp corners on its graph, it is continuous; lim,,xo f(x) = f(x,) at each point x,. (d) Here lim,,, f(x) = 1, so the limit exists. However, the limit does not equal f(1) = 2. Thus f is not continuous at x, = 1. It is continuous on the intervals (- m, 1) and (1, m). A In Section 1.2, we used various limit theorems to establish the continuity of functions that are basic to calculus. For example, the rational function rule for limits says that a rational function is continuous at points where its denominator does not vanish. Example 2 Show that the function f(x) = (x - 1)/3x2 is continuous at x, = 4. Solution This is a rational function whose denominator does not vanish at x, = 4, so it is continuous by the rational function rule. A Example 3 Let g(x) be the step function defined by Show that g is not continuous at x, = 0. Sketch. Copyright 1985 Springer-Verlag. All rights reserved. 3.1 Continuity and the Intermediate Value Theorem 141 Figure 3.1.3. This step function is discontinuous at x,, = 0. Solution The graph of g is shown in Fig. 3.1.3. Since g approaches (in fact, equals) 0 as x approaches 0 from the left, but approaches 1 as x approaches 0 from the right, lim,,,g(x) does not exist. Therefore, g is not continuous at x, = 0. A Example 4 Using the laws of limits, show that iff and g are continuous at x,, so is fg. Solution We must show that limXjxo( fg)(x) = ( fg)(x,). By the product rule for limits, limxjxo[f(x)g(x)l = Ilim,,,of(x>l[limx jxog(x)l.= f(xo)g(xo), since f and g are continuous at x,. But f(x,)g(x,) = (fg)(x,), and so lim,,,o< fg>(x) = ( fg)(xo), as required. A In Section 1.3, we proved the following theorem: f is differentiable at x,, then f is continuous at x,. Using our knowledge of differential calculus, we can use this relationship to establish the continuity of additional functions or to confirm the continuity of functions originally determined using the laws of limits. Example 5 (a) Show that f(x) = 3x2/(x3- 2) is continuous at x, = I. Where else is it continuous? (b) Show thaiflx) = is continuous at x = 0. Solution (a) By our rules for differentiation, we see that this function is differentiable at x, = 1; indeed, x3 - 2 does not vanish at x, = 1. Thus f is also continuous at x, = 1. Similarly, f is continuous at each x, such that xi - 2.5: 0, i.e., at each x, # 3$. (b) This function is the composition of the square root function h(u) = & and the function g(x) = x2+ 2x + 1; f(x) = h(g(x)). Note that g(0) = 1 > 0. Since g is differentiable at any x (being a polynomial), and h is differentia- ble at u = l, f is differentiable at x = 0 by the chain rule. Thus f is continuous at x = 0. A According to our previous discussion, a continuous function is one whose graph never "jumps." The definition of continuity is local since continuity at each point involves values of the function only near that point. There is a corresponding global statement, called the intermediate value theorem, which involves the behavior of a function over an entire interval [a, b]. Let f be continuous1 on [a, b] and suppose that, for some number c, f (a) < c < f (b) or f(a) > c > f (b). Then there is some point x, in (a, b) such that f (x,) = c. ' Our definition of continuity on [a,b] assumes that f is defined near each point 2 of [a,b], including the endpoints, and that lim,, f(x) = f(SZ). Actually, at the endpoints, it is enough to assume that the one-sided limits (from inside the interval) exist, rather than the two-sided ones. Copyright 1985 Springer-Verlag. All rights reserved. 142 Chapter 3 Graphing and Maximum-Minimum Problems In geometric terms, this theorem says that for the graph of a continuous function to pass from one side of a horizontal line to the other, the graph must meet the line somewhere (see Fig. 3.1.4). The proof of the theorem depends on a careful study of properties of the real numbers and will be omitted. (See the references listed in the Preface.) However, by drawing additional graphs like those in Fig. 3.1.4, you should convince yourself that the theorem is reason- able. Figure 3.1.4. The graph off must pierce the horizontal liney = c if it is to get across. Example 6 Show that there is a number x, such that xi - x, = 3. Solution Let f(x) = x5 - x. Then f(0) = 0 and f(2) = 30. Since 0 < 3 < 30, the interme- diate value theorem guarantees that there is a number x, in (0,2) such that f(x,) = 3. (The function f is continuous on [O, 21 because it is a polynomial.) A Notice that the intermediate value theorem does not tell us how to find the number x, but merely that it exists. (A look at Fig. 3.1.4 should convince you that there may be more than one possible choice for x,.) Nevertheless, by repeatedly dividing an interval into two or more parts and evaluating f(x) at the dividing points, we can solve the equation f(xo) = c as accurately as we wish. This method of bisection is illustrated in the next example. @ Example 7 (The method of bisection) Find a solution of the equation x5 - x = 3 in (0,2) to within an accuracy of 0.1 by repeatedly dividing intervals in half and testing each half for a root. Solution In Example 6 we saw that the equation has a solution in the interval (0,2). To locate the solution more precisely, we evaluate f(l) = l5 - 1 = 0. Thus f(1) < 3 < f(2), so there is a root in (1,2). Now we bisect [1,2] into [l, 1.51 and [1.5,2] and repeat: f(1.5) x 6.09 > 3. so there is a root in (1, 1.5); f(1.25) = 1.80 < 3, so there is a root in (1.25, 1.5); f(1.375)% 3.54 > 3, so there is a root in (1.25, 1.375); thus x, = 1.3 is within 0.1 of a root. Further accuracy can be obtained by means of further bisections. (Related techniques for root finding are suggested in the exercises for this section. Other methods are presented in Section 1 1.4.) A There is another useful way of stating the intermediate value theorem (the contrapositive statement).
Load more

Recommended publications
  • Plotting, Derivatives, and Integrals for Teaching Calculus in R
    Plotting, Derivatives, and Integrals for Teaching Calculus in R Daniel Kaplan, Cecylia Bocovich, & Randall Pruim July 3, 2012 The mosaic package provides a command notation in R designed to make it easier to teach and to learn introductory calculus, statistics, and modeling. The principle behind mosaic is that a notation can more effectively support learning when it draws clear connections between related concepts, when it is concise and consistent, and when it suppresses extraneous form. At the same time, the notation needs to mesh clearly with R, facilitating students' moving on from the basics to more advanced or individualized work with R. This document describes the calculus-related features of mosaic. As they have developed histori- cally, and for the main as they are taught today, calculus instruction has little or nothing to do with statistics. Calculus software is generally associated with computer algebra systems (CAS) such as Mathematica, which provide the ability to carry out the operations of differentiation, integration, and solving algebraic expressions. The mosaic package provides functions implementing he core operations of calculus | differen- tiation and integration | as well plotting, modeling, fitting, interpolating, smoothing, solving, etc. The notation is designed to emphasize the roles of different kinds of mathematical objects | vari- ables, functions, parameters, data | without unnecessarily turning one into another. For example, the derivative of a function in mosaic, as in mathematics, is itself a function. The result of fitting a functional form to data is similarly a function, not a set of numbers. Traditionally, the calculus curriculum has emphasized symbolic algorithms and rules (such as xn ! nxn−1 and sin(x) ! cos(x)).
    [Show full text]
  • Optimization and Gradient Descent INFO-4604, Applied Machine Learning University of Colorado Boulder
    Optimization and Gradient Descent INFO-4604, Applied Machine Learning University of Colorado Boulder September 11, 2018 Prof. Michael Paul Prediction Functions Remember: a prediction function is the function that predicts what the output should be, given the input. Prediction Functions Linear regression: f(x) = wTx + b Linear classification (perceptron): f(x) = 1, wTx + b ≥ 0 -1, wTx + b < 0 Need to learn what w should be! Learning Parameters Goal is to learn to minimize error • Ideally: true error • Instead: training error The loss function gives the training error when using parameters w, denoted L(w). • Also called cost function • More general: objective function (in general objective could be to minimize or maximize; with loss/cost functions, we want to minimize) Learning Parameters Goal is to minimize loss function. How do we minimize a function? Let’s review some math. Rate of Change The slope of a line is also called the rate of change of the line. y = ½x + 1 “rise” “run” Rate of Change For nonlinear functions, the “rise over run” formula gives you the average rate of change between two points Average slope from x=-1 to x=0 is: 2 f(x) = x -1 Rate of Change There is also a concept of rate of change at individual points (rather than two points) Slope at x=-1 is: f(x) = x2 -2 Rate of Change The slope at a point is called the derivative at that point Intuition: f(x) = x2 Measure the slope between two points that are really close together Rate of Change The slope at a point is called the derivative at that point Intuition: Measure the
    [Show full text]
  • Calculus Terminology
    AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential
    [Show full text]
  • Maxima and Minima
    Basic Mathematics Maxima and Minima R Horan & M Lavelle The aim of this document is to provide a short, self assessment programme for students who wish to be able to use differentiation to find maxima and mininima of functions. Copyright c 2004 [email protected] , [email protected] Last Revision Date: May 5, 2005 Version 1.0 Table of Contents 1. Rules of Differentiation 2. Derivatives of order 2 (and higher) 3. Maxima and Minima 4. Quiz on Max and Min Solutions to Exercises Solutions to Quizzes Section 1: Rules of Differentiation 3 1. Rules of Differentiation Throughout this package the following rules of differentiation will be assumed. (In the table of derivatives below, a is an arbitrary, non-zero constant.) y axn sin(ax) cos(ax) eax ln(ax) dy 1 naxn−1 a cos(ax) −a sin(ax) aeax dx x If a is any constant and u, v are two functions of x, then d du dv (u + v) = + dx dx dx d du (au) = a dx dx Section 1: Rules of Differentiation 4 The stationary points of a function are those points where the gradient of the tangent (the derivative of the function) is zero. Example 1 Find the stationary points of the functions (a) f(x) = 3x2 + 2x − 9 , (b) f(x) = x3 − 6x2 + 9x − 2 . Solution dy (a) If y = 3x2 + 2x − 9 then = 3 × 2x2−1 + 2 = 6x + 2. dx The stationary points are found by solving the equation dy = 6x + 2 = 0 . dx In this case there is only one solution, x = −1/3.
    [Show full text]
  • Calculus 120, Section 7.3 Maxima & Minima of Multivariable Functions
    Calculus 120, section 7.3 Maxima & Minima of Multivariable Functions notes by Tim Pilachowski A quick note to start: If you’re at all unsure about the material from 7.1 and 7.2, now is the time to go back to review it, and get some help if necessary. You’ll need all of it for the next three sections. Just like we had a first-derivative test and a second-derivative test to maxima and minima of functions of one variable, we’ll use versions of first partial and second partial derivatives to determine maxima and minima of functions of more than one variable. The first derivative test for functions of more than one variable looks very much like the first derivative test we have already used: If f(x, y, z) has a relative maximum or minimum at a point ( a, b, c) then all partial derivatives will equal 0 at that point. That is ∂f ∂f ∂f ()a b,, c = 0 ()a b,, c = 0 ()a b,, c = 0 ∂x ∂y ∂z Example A: Find the possible values of x, y, and z at which (xf y,, z) = x2 + 2y3 + 3z 2 + 4x − 6y + 9 has a relative maximum or minimum. Answers : (–2, –1, 0); (–2, 1, 0) Example B: Find the possible values of x and y at which fxy(),= x2 + 4 xyy + 2 − 12 y has a relative maximum or minimum. Answer : (4, –2); z = 12 Notice that the example above asked for possible values. The first derivative test by itself is inconclusive. The second derivative test for functions of more than one variable is a good bit more complicated than the one used for functions of one variable.
    [Show full text]
  • Mean Value, Taylor, and All That
    Mean Value, Taylor, and all that Ambar N. Sengupta Louisiana State University November 2009 Careful: Not proofread! Derivative Recall the definition of the derivative of a function f at a point p: f (w) − f (p) f 0(p) = lim (1) w!p w − p Derivative Thus, to say that f 0(p) = 3 means that if we take any neighborhood U of 3, say the interval (1; 5), then the ratio f (w) − f (p) w − p falls inside U when w is close enough to p, i.e. in some neighborhood of p. (Of course, we can’t let w be equal to p, because of the w − p in the denominator.) In particular, f (w) − f (p) > 0 if w is close enough to p, but 6= p. w − p Derivative So if f 0(p) = 3 then the ratio f (w) − f (p) w − p lies in (1; 5) when w is close enough to p, i.e. in some neighborhood of p, but not equal to p. Derivative So if f 0(p) = 3 then the ratio f (w) − f (p) w − p lies in (1; 5) when w is close enough to p, i.e. in some neighborhood of p, but not equal to p. In particular, f (w) − f (p) > 0 if w is close enough to p, but 6= p. w − p • when w > p, but near p, the value f (w) is > f (p). • when w < p, but near p, the value f (w) is < f (p). Derivative From f 0(p) = 3 we found that f (w) − f (p) > 0 if w is close enough to p, but 6= p.
    [Show full text]
  • Math 105: Multivariable Calculus Seventeenth Lecture (3/17/10)
    Daily Summary Fast Taylor Series Critical Points and Extrema Lagrange Multipliers Math 105: Multivariable Calculus Seventeenth Lecture (3/17/10) Steven J Miller Williams College [email protected] http://www.williams.edu/go/math/sjmiller/ public html/341/ Bronfman Science Center Williams College, March 17, 2010 1 Daily Summary Fast Taylor Series Critical Points and Extrema Lagrange Multipliers Summary for the Day 2 Daily Summary Fast Taylor Series Critical Points and Extrema Lagrange Multipliers Summary for the day Fast Taylor Series. Critical Points and Extrema. Constrained Maxima and Minima. 3 Daily Summary Fast Taylor Series Critical Points and Extrema Lagrange Multipliers Fast Taylor Series 4 Daily Summary Fast Taylor Series Critical Points and Extrema Lagrange Multipliers Formula for Taylor Series Notation: f twice differentiable function ∂f ∂f Gradient: f =( ∂ ,..., ∂ ). ∇ x1 xn Hessian: ∂2f ∂2f ∂x1∂x1 ∂x1∂xn . ⋅⋅⋅. Hf = ⎛ . .. ⎞ . ∂2f ∂2f ⎜ ∂ ∂ ∂ ∂ ⎟ ⎝ xn x1 ⋅⋅⋅ xn xn ⎠ Second Order Taylor Expansion at −→x 0 1 T f (−→x 0) + ( f )(−→x 0) (−→x −→x 0)+ (−→x −→x 0) (Hf )(−→x 0)(−→x −→x 0) ∇ ⋅ − 2 − − T where (−→x −→x 0) is the row vector which is the transpose of −→x −→x 0. − − 5 Daily Summary Fast Taylor Series Critical Points and Extrema Lagrange Multipliers Example 3 Let f (x, y)= sin(x + y) + (x + 1) y and (x0, y0) = (0, 0). Then ( f )(x, y) = cos(x + y)+ 3(x + 1)2y, cos(x + y) + (x + 1)3 ∇ and sin(x + y)+ 6(x + 1)2y sin(x + y)+ 3(x + 1)2 (Hf )(x, y) = − − , sin(x + y)+ 3(x + 1)2 sin(x + y) − − so 0 3 f (0, 0)= 0, ( f )(0, 0) = (1, 2), (Hf )(0, 0)= ∇ 3 0 which implies the second order Taylor expansion is 1 0 3 x 0 + (1, 2) (x, y)+ (x, y) ⋅ 2 3 0 y 1 3y = x + 2y + (x, y) = x + 2y + 3xy.
    [Show full text]
  • Lecture 13: Extrema
    Math S21a: Multivariable calculus Oliver Knill, Summer 2013 Lecture 13: Extrema An important problem in multi-variable calculus is to extremize a function f(x, y) of two vari- ables. As in one dimensions, in order to look for maxima or minima, we consider points, where the ”derivative” is zero. A point (a, b) in the plane is called a critical point of a function f(x, y) if ∇f(a, b) = h0, 0i. Critical points are candidates for extrema because at critical points, all directional derivatives D~vf = ∇f · ~v are zero. We can not increase the value of f by moving into any direction. This definition does not include points, where f or its derivative is not defined. We usually assume that a function is arbitrarily often differentiable. Points where the function has no derivatives are not considered part of the domain and need to be studied separately. For the function f(x, y) = |xy| for example, we would have to look at the points on the coordinate axes separately. 1 Find the critical points of f(x, y) = x4 + y4 − 4xy + 2. The gradient is ∇f(x, y) = h4(x3 − y), 4(y3 − x)i with critical points (0, 0), (1, 1), (−1, −1). 2 f(x, y) = sin(x2 + y) + y. The gradient is ∇f(x, y) = h2x cos(x2 + y), cos(x2 + y) + 1i. For a critical points, we must have x = 0 and cos(y) + 1 = 0 which means π + k2π. The critical points are at ... (0, −π), (0, π), (0, 3π),.... 2 2 3 The graph of f(x, y) = (x2 + y2)e−x −y looks like a volcano.
    [Show full text]
  • 5 Graph Theory
    last edited March 21, 2016 5 Graph Theory Graph theory – the mathematical study of how collections of points can be con- nected – is used today to study problems in economics, physics, chemistry, soci- ology, linguistics, epidemiology, communication, and countless other fields. As complex networks play fundamental roles in financial markets, national security, the spread of disease, and other national and global issues, there is tremendous work being done in this very beautiful and evolving subject. The first several sections covered number systems, sets, cardinality, rational and irrational numbers, prime and composites, and several other topics. We also started to learn about the role that definitions play in mathematics, and we have begun to see how mathematicians prove statements called theorems – we’ve even proven some ourselves. At this point we turn our attention to a beautiful topic in modern mathematics called graph theory. Although this area was first introduced in the 18th century, it did not mature into a field of its own until the last fifty or sixty years. Over that time, it has blossomed into one of the most exciting, and practical, areas of mathematical research. Many readers will first associate the word ‘graph’ with the graph of a func- tion, such as that drawn in Figure 4. Although the word graph is commonly Figure 4: The graph of a function y = f(x). used in mathematics in this sense, it is also has a second, unrelated, meaning. Before providing a rigorous definition that we will use later, we begin with a very rough description and some examples.
    [Show full text]
  • Some Recent Developments in the Calculus of Variations.*
    1920.] THE CALCULUS OF VARIATIONS. 343 SOME RECENT DEVELOPMENTS IN THE CALCULUS OF VARIATIONS.* BY PROFESSOR GILBERT AMES BLISS. IT is my purpose to speak this afternoon of a part of the theory of the calculus of variations which has aroused the interest and taxed the ingenuity of a sequence of mathe­ maticians beginning with Legendre, and extending by way of Jacobi, Clebsch, Weierstrass, and a numerous array of others, to the present time. The literature of the subject is very large and is still growing. I was discussing recently the title of this address with a fellow mathematician who remarked that he was not aware that there had been any recent progress in the calculus of variations. This was a very natural sus­ picion, I think, in view of the fact that the attention of most mathematicians of the present time seems irresistibly attracted to such subjects as integral equations and their generaliza­ tions, the theory of definite integration, and the theory of functions of lines. It is indeed in these latter domains that the activities especially characteristic of the present era are centered, and the progress already made in them, and the further progress inevitable in the near future, will doubtless be sufficient alone to insure for our generation of mathematical workers a noteworthy place in the history of the science. While speaking of present day mathematical tendencies I should like to take occasion to mention a remark which has been made to me a number of times by persons who are inter­ ested in mathematics primarily for its applications.
    [Show full text]
  • Lecture 11: Graphs of Functions Definition If F Is a Function With
    Lecture 11: Graphs of Functions Definition If f is a function with domain A, then the graph of f is the set of all ordered pairs f(x; f(x))jx 2 Ag; that is, the graph of f is the set of all points (x; y) such that y = f(x). This is the same as the graph of the equation y = f(x), discussed in the lecture on Cartesian co-ordinates. The graph of a function allows us to translate between algebra and pictures or geometry. A function of the form f(x) = mx+b is called a linear function because the graph of the corresponding equation y = mx + b is a line. A function of the form f(x) = c where c is a real number (a constant) is called a constant function since its value does not vary as x varies. Example Draw the graphs of the functions: f(x) = 2; g(x) = 2x + 1: Graphing functions As you progress through calculus, your ability to picture the graph of a function will increase using sophisticated tools such as limits and derivatives. The most basic method of getting a picture of the graph of a function is to use the join-the-dots method. Basically, you pick a few values of x and calculate the corresponding values of y or f(x), plot the resulting points f(x; f(x)g and join the dots. Example Fill in the tables shown below for the functions p f(x) = x2; g(x) = x3; h(x) = x and plot the corresponding points on the Cartesian plane.
    [Show full text]
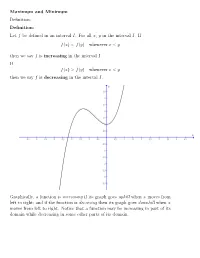
  • Maximum and Minimum Definition
    Maximum and Minimum Definition: Definition: Let f be defined in an interval I. For all x, y in the interval I. If f(x) < f(y) whenever x < y then we say f is increasing in the interval I. If f(x) > f(y) whenever x < y then we say f is decreasing in the interval I. Graphically, a function is increasing if its graph goes uphill when x moves from left to right; and if the function is decresing then its graph goes downhill when x moves from left to right. Notice that a function may be increasing in part of its domain while decreasing in some other parts of its domain. For example, consider f(x) = x2. Notice that the graph of f goes downhill before x = 0 and it goes uphill after x = 0. So f(x) = x2 is decreasing on the interval (−∞; 0) and increasing on the interval (0; 1). Consider f(x) = sin x. π π 3π 5π 7π 9π f is increasing on the intervals (− 2 ; 2 ), ( 2 ; 2 ), ( 2 ; 2 )...etc, while it is de- π 3π 5π 7π 9π 11π creasing on the intervals ( 2 ; 2 ), ( 2 ; 2 ), ( 2 ; 2 )...etc. In general, f = sin x is (2n+1)π (2n+3)π increasing on any interval of the form ( 2 ; 2 ), where n is an odd integer. (2m+1)π (2m+3)π f(x) = sin x is decreasing on any interval of the form ( 2 ; 2 ), where m is an even integer. What about a constant function? Is a constant function an increasing function or decreasing function? Well, it is like asking when you walking on a flat road, as you going uphill or downhill? From our definition, a constant function is neither increasing nor decreasing.
    [Show full text]