Modeling Voltage-Controlled Resistors and Capacitors in Pspice
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

TRANSIENT STABILITY of the WIEN BRIDGE OSCILLATOR I
TRANSIENT STABILITY OF THE WIEN BRIDGE OSCILLATOR i TRANSIENT STABILITY OF THE WIEN BRIDGE OSCILLATOR by RICHARD PRESCOTT SKILLEN, B. Eng. A Thesis Submitted ··to the Faculty of Graduate Studies in Partial Fulfilment of the Requirements for the Degree Master of Engineering McMaster University May 1964 ii MASTER OF ENGINEERING McMASTER UNIVERSITY (Electrical Engineering) Hamilton, Ontario TITLE: Transient Stability of the Wien Bridge Oscillator AUTHOR: Richard Prescott Skillen, B. Eng., (McMaster University) NUMBER OF PAGES: 105 SCOPE AND CONTENTS: In many Resistance-Capacitance Oscillators the oscillation amplitude is controlled by the use of a temperature-dependent resistor incorporated in the negative feedback loop. The use of thermistors and tungsten lamps is discussed and an approximate analysis is presented for the behaviour of the tungsten lamp. The result is applied in an analysis of the familiar Wien Bridge Oscillator both for the presence of a linear circuit and a cubic nonlinearity. The linear analysis leads to a highly unstable transient response which is uncommon to most oscillators. The inclusion of the slight cubic nonlinearity, however, leads to a result which is in close agreement to the observed response. ACKNOWLEDGEMENTS: The author wishes to express his appreciation to his supervisor, Dr. A.S. Gladwin, Chairman of the Department of Electrical Engineering for his time and assistance during the research work and preparation of the thesis. The author would also like to thank Dr. Gladwin and all his other undergraduate professors for encouragement and instruction in the field of circuit theor.y. Acknowledgement is also made for the generous financial support of the thesis project by the Defence Research Board·under grant No. -

Oscillator Circuits
Oscillator Circuits 1 II. Oscillator Operation For self-sustaining oscillations: • the feedback signal must positive • the overall gain must be equal to one (unity gain) 2 If the feedback signal is not positive or the gain is less than one, then the oscillations will dampen out. If the overall gain is greater than one, then the oscillator will eventually saturate. 3 Types of Oscillator Circuits A. Phase-Shift Oscillator B. Wien Bridge Oscillator C. Tuned Oscillator Circuits D. Crystal Oscillators E. Unijunction Oscillator 4 A. Phase-Shift Oscillator 1 Frequency of the oscillator: f0 = (the frequency where the phase shift is 180º) 2πRC 6 Feedback gain β = 1/[1 – 5α2 –j (6α – α3) ] where α = 1/(2πfRC) Feedback gain at the frequency of the oscillator β = 1 / 29 The amplifier must supply enough gain to compensate for losses. The overall gain must be unity. Thus the gain of the amplifier stage must be greater than 1/β, i.e. A > 29 The RC networks provide the necessary phase shift for a positive feedback. They also determine the frequency of oscillation. 5 Example of a Phase-Shift Oscillator FET Phase-Shift Oscillator 6 Example 1 7 BJT Phase-Shift Oscillator R′ = R − hie RC R h fe > 23 + 29 + 4 R RC 8 Phase-shift oscillator using op-amp 9 B. Wien Bridge Oscillator Vi Vd −Vb Z2 R4 1 1 β = = = − = − R3 R1 C2 V V Z + Z R + R Z R β = 0 ⇒ = + o a 1 2 3 4 1 + 1 3 + 1 R4 R2 C1 Z2 R4 Z2 Z1 , i.e., should have zero phase at the oscillation frequency When R1 = R2 = R and C1 = C2 = C then Z + Z Z 1 2 2 1 R 1 f = , and 3 ≥ 2 So frequency of oscillation is f = 0 0 2πRC R4 2π ()R1C1R2C2 10 Example 2 Calculate the resonant frequency of the Wien bridge oscillator shown above 1 1 f0 = = = 3120.7 Hz 2πRC 2 π(51×103 )(1×10−9 ) 11 C. -

Van Der Pol Approximation Applied to Wien Oscillators João Casaleiroa,B,∗, Luís B
Available online at www.sciencedirect.com ScienceDirect Procedia Technology 17 ( 2014 ) 335 – 342 Conference on Electronics, Telecommunications and Computers – CETC 2013 Van der Pol Approximation Applied to Wien Oscillators João Casaleiroa,b,∗, Luís B. Oliveirab, António C. Pintoa aDep. of Electronics, Telecommunications and Computers Engineering, Instituto Superior de Engenharia de Lisboa - ISEL, Lisboa, Portugal bDepartment of Electrical Engineering, FCT, CTS-Uninova, Caparica, Portugal Abstract This paper presents a nonlinear analysis of the Wien type oscillators based on the Van der Pol approximation. The steady-state equations for the key parameters, frequency and amplitude, are derived and their sensitivities to ambient temperature are discussed. The added value of this work is to present an analytical method to obtain the fundamental characteristics of the Wien type oscillators and to relate these characteristics with the circuit parameters in a simpler manner. The simulation results confirm the amplitude and frequency equations, and confirm that the amplitude is controlled by the limiter circuit. ©c 20142014 TheThe Authors. Authors. Published Published byby Elsevier Elsevier Ltd. Ltd. This is an open access article under the CC BY-NC-ND license (Selectionhttp://creativecommons.org/licenses/by-nc-nd/3.0/ and peer-review under responsibility of ISEL). – Instituto Superior de Engenharia de Lisboa. Peer-review under responsibility of ISEL – Instituto Superior de Engenharia de Lisboa, Lisbon, PORTUGAL. Keywords: Oscillator, Wien oscillator, quasi-sinusoidal, Van der Pol, amplitude stabilization. 1. Introduction The oscillators of the Wien type are well known, second order, quasi-sinusoidal oscillators, suited for low frequencies and low distortion applications [1]. The low-distortion feature of this type of oscillator justifies its use for the characterization of analog-to-digital converters (ADC)[2], instrumentation circuits and a wide variety of measurement circuits. -

PH-218 Lec-16: Oscillator
Analog & Digital Electronics Course No: PH-218 Lec-16: Oscillator Course Instructors: Dr. A. P. VAJPEYI Department of Physics, Indian Institute of Technology Guwahati, India 1 Positive Feedback When input and feedback signal both are in same phase, It is called a positive feedback. Positive feedback is used in analog and digital systems. A primary use of +ve feedback is in the production of oscillators. + Vi Vs Σ A( f) Vo + Vf SelectiveNetwork β(f) V A o = V = AV = A(V +V ) and V f = βVo o i s f Vs 1− Aβ Barkhausen Criterion: for oscillator βA=1 and +ve feedback 2 Oscillator Circuit Oscillator is an electronic circuit which converts dc signal into ac signal. Oscillator is basically a positive feedback amplifier with unity loop gain. For an inverting amplifier- feedback network provides a phase shift of 180 °°° while for non-inverting amplifier- feedback network provides a phase shift of 0°°° to get positive feedback . Vo A = If βA=1 then V o = ∞ ; Very high output with zero input. Vs 1− Aβ Use positive feedback through frequency-selective feedback network to ensure sustained oscillation at ω0 Use of Oscillator Circuits Clock input for CPU, DSP chips … Local oscillator for radio receivers, mobile receivers, etc As a signal generators in the lab Clock input for analog-digital and digital-analog converters 3 Oscillators If the feedback signal is not positive and gain is less than unity, oscillations dampen out. If the gain is higher than unity then oscillation saturates. Type of Oscillators Oscillators can be categorized according to the types of feedback network used: RC Oscillators: Phase shift and Wien Bridge Oscillators LC Oscillators: Colpitt and Hartley Oscillators Crystal Oscillators 4 RC Oscillators R −1 X C Vo = ( )Vin and φ = tan ( ) R − jX c R o o Φ =0 if Xc=0 and Φ =90 if R=0 However adjusting R to zero is impractical because it would lead to no voltage across R, thus in a RC circuit, phase shift is always ≤ 90 o and it is a function of frequency. -
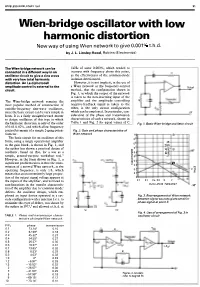
Wien-Bridge Oscillator with Low Harmonic Distortion
WIRELESS WORLD MAY 1981 51 Wien-bridge oscillator with low harmonic distortion New way of using Wien network to give 0.001 % t.h.d. by J. L. Linsley Hood, Robins (Electronics) The Wien-bridge network can be 1kHz of some 0.003%, which tended to connected in a different way in an increase with frequency above this point, R oscillator circuit to give a sine wave as the effectiveness of the common-mode with very low total harmonic isolation deteriorated. distortion. An I.e.d/photocell However, it is not implicit, in the use of a Wien network as the frequency-control amplitude control is external to the Output circuit. method, that the configuration shown in Fig. 1, in which the output of the network is taken to the non-inverting input of the R The Wien-bridge network remains the amplifier and the amplitude controlling most popular method of construction of negative-feedback signal is taken to the variable-frequency sine-wave oscillators, other, is the only circuit configuration since the basic circuit can be very simple in which can be employed. In particular, con ov form. It is a fairly straightforward matter sideration of the phase and transmission to design oscillators of this type in which characteristics of such a network, shown in Table 1 and Fig. 2 for equal values of C the harmonic distortion is only of the order Fig. 1. Basic Wien-bridge oscillator circuit of 0.01-0.02%, and which allow frequency control by means of a simple 2-gang poten Fig. -

The Barkhausen Criterion (Observation ?)
View metadata,Downloaded citation and from similar orbit.dtu.dk papers on:at core.ac.uk Dec 17, 2017 brought to you by CORE provided by Online Research Database In Technology The Barkhausen Criterion (Observation ?) Lindberg, Erik Published in: Proceedings of NDES 2010 Publication date: 2010 Document Version Publisher's PDF, also known as Version of record Link back to DTU Orbit Citation (APA): Lindberg, E. (2010). The Barkhausen Criterion (Observation ?). In Proceedings of NDES 2010 (pp. 15-18). Dresden, Germany. General rights Copyright and moral rights for the publications made accessible in the public portal are retained by the authors and/or other copyright owners and it is a condition of accessing publications that users recognise and abide by the legal requirements associated with these rights. • Users may download and print one copy of any publication from the public portal for the purpose of private study or research. • You may not further distribute the material or use it for any profit-making activity or commercial gain • You may freely distribute the URL identifying the publication in the public portal If you believe that this document breaches copyright please contact us providing details, and we will remove access to the work immediately and investigate your claim. 18th IEEE Workshop on Nonlinear Dynamics of Electronic Systems (NDES2010) The Barkhausen Criterion (Observation ?) Erik Lindberg, IEEE Life member Faculty of Electrical Eng. & Electronics, 348 Technical University of Denmark, DK-2800 Kongens Lyngby, Denmark Email: [email protected] Abstract—A discussion of the Barkhausen Criterion which is a necessary but NOT sufficient criterion for steady state oscillations of an electronic circuit. -

Wien Bridge Oscillator
Wien Bridge Oscillator Conventional analysis Consider the amplifier shown below. The potential at the noninverting input is equal to the input signal: v+ = vi . The potential at the invertiing input is related to the output via a voltage-divider: Rf1 v− = vo . Rf1 + Rf2 Using the ideal op-amp assumption that v+ = v– leads to vo = Gvi where Rf2 G ≡ 1 + . Rf1 This is the standard non-inverting amplifier configuration. Now let's ask if we can sustain a finite output if, instead of an external input, we feed the output back to the input through a frequency-dependent network. Using complex phasor notation such that v = ℝVê jωt (where ℝ means "real part of") , we write Vî = H(ω)Vô . We also had Vô = G(ω)Vi.̂ (Note: in the current case G actually does not have any frequency dependence. The notation is for purposes of generality.) Self-consistency requires Vî = G(ω)H(ω)Vi.̂ This requires that the loop gain G(ω)H(ω) = 1. This is the Barkhausen condition for oscillation, which implies both that the magnitude of the loop gain is unity and that the phase shift is zero or a multiple of 2π . Wien Bridge Consider the resistance - capacitance network shown above. Z1 i = o. Z1 Vî = Vô . Z1 + Z2 R 1+jωRC Vî = Vô . R R j 1 1+jωRC + ( − ωC ) 1 Vî = Vô . j ωRC 1 3 + ( − ωRC ) Thus 1 H(ω) = . j ωRC 1 3 + ( − ωRC ) Remember that Vô = GVî with G having the real value Rf2 G = 1 + Rf1 . -

CHAPTER Feedback Amplifier & Oscillators
Analog Circuits Day-12 Oscillators Introduction to Feedback: The phenomenon of feeding a portion of the output signal back to the input circuit is known as feedback. The effect results in a dependence between the output and the input and an effective control can be obtained in the working of the circuit. Feedback is of two types. • Negative Feedback • Positive Feedback Negative or Degenerate feedback: • In negative feedback, the feedback energy (voltage or current), is out of phase with the input signal and thus opposes it. • Negative feedback reduces gain of the amplifier. It also reduce distortion, noise and instability. • This feedback increases bandwidth and improves input and output impedances. • Due to these advantages, the negative feedback is frequently used in amplifiers. NegativeFeedback Positive or regenerate feedback: • In positive feedback, the feedback energy (voltage or currents), is in phase with the input signal and thus aids it. Positive feedback increases gain of the amplifier also increases distortion, noise and instability. • Because of these disadvantages, positive feedback is seldom employed in amplifiers. But the positive feedback is used in oscillators. Positive Feedback In the above figure, the gain of the amplifier is represented as A. The gain of the amplifier is the ratio of output voltage Vo to the input voltage Vi. The feedback network extracts a voltage Vf = β Vo from the output Vo of the amplifier. This voltage is subtracted for negative feedback, from the signal voltage Vs. Now, Vi=Vs + Vf =Vs+βVo The quantity β = Vf/Vo is called as feedback ratio or feedback fraction. The output Vo must be equal to the input voltage (Vs + βVo) multiplied by the gain A of the amplifier. -

Operational Amplifiers Is That the User Often Finds That They Oscillate in Connections He Wishes Were Stable
CHAPTER XII ADVANCED APPLICATIONS 12.1 SINUSOIDAL OSCILLATORS One of the major hazards involved in the application of operational amplifiers is that the user often finds that they oscillate in connections he wishes were stable. An objective of this book is to provide guidance to help circumvent this common pitfall. There are, however, many applications that require a periodic waveform with a controlled frequency, waveshape, and amplitude, and operational amplifiers are frequently used to generate these signals. If a sinusoidal output is required, the conditions that must be satisfied to generate this waveform can be determined from the linear feedback theory presented in earlier chapters. 12.1.1 The Wien-Bridge Oscillator The Wien-bridge corifiguration (Fig. 12.1) is one way to implement a sinusoidal oscillator. The transfer function of the network that connects the output of the amplifier to its noninverting input is (in the absence of loading) V.(s) _ RCs 2 V0(s) ~ R Cess + 3RCs + 1 The operational amplifier is connected for a noninverting gain of 3. Com bining this gain with Eqn. 12.1 yields for a loop transmission in this positive-feedback system 3RCs L(s) = C2s 2 3RCs (12.2) R2Cs + 3RCs + 1 The characteristic equation 3RCs R2C2 s2 + 1 I - L(s) = 1 - 3RsR222+1 (12.3) R2C2 s 2 + 3RCs + 1 R2 C2s 2 + 3RCs + 1 has imaginary zeros at s = ±(j/RC), and thus the system can sustain constant-amplitude sinusoidal oscillations at a frequency w = 1/RC. 485 486 Advanced Applications 2R, R R C +0 Va C R Figure 12.1 Wien-bridge oscillator. -

Wien Bridge Oscillator
Wien Bridge Oscillator Introduction Oscillators are circuits that produce periodic waveforms without any input signal. They generally use some form of active devices like transistors or OPAMPs as amplifiers with feedback network consisting of passive devices such as resistors, capacitors, or inductors. Fig.1 demonstrates the a basic negative feedback system in which VIN is the input voltage, VOUT is the output voltage from the amplifier gain block (A), and β as the feedback factor, that is fed back to the summing junction. E represents the error signal that is equal to the summation of the feedback factor and the input voltage. Figure 1 Basic block diagram explaining feedback When Aβ = 1, i.e. the unity loop gain with phase shift of 180° provided by the feedback network (Aβ= 1∠–180°), the denominator term becomes 0 and the gain with feedback, , becomes infinite. This means infinitesimal signal (noise voltage) can provide an output voltage, and the circuit acts as an oscillator even without an input signal. This is Barkhausen Criterion for sustained oscillations. This can be explained using control theory using following three conditions: 1. If the loop gain Aβ <1, the poles of the transfer function Af, lie in the left half of the s-Plane (real part σ being negative). The system oscillates but eventually they die out. (Refer Fig 2a) 2. If the loop gain Aβ=1, the poles of the transfer function (which are complex conjugates with real part σ equal to zero) of the closed loop system lie on the jω axis. However, in reality, the nonlinearity of the circuit components eventually causes Aβ to become less than one and the oscillations cease out. -

INSTITUTION Controlledoscillators. Each Lesson Follows a Typical
DOCUMENT RESUME ED 190 906 CE 026 591 TITLE ' Military Curricula'for Vocational & Technical . Education. Baied Electricity and Electronics*. CANTRAC A-100%0010. Module 32: Intermediate Oscillators. Study Booklet. INSTITUTION Chief of Naial Education and Training Support, Pensacola, Fla.: Ohio State Univ., Columbus. National Center for Research in Vocational Education. '. FEPORT No CMTT-E-050 rut DATE Jul BO NOTE 262p.:Forfrelateddocuments see CE 026 560-593. --, , EDRS PRICE MFO1 /PC11 Plus Postage. DESCFIFTORS . *Electricty: *Electronics: Individualized Instruction: Learning Activities: Learning Modules: Postsecondary Education: Programed Instruction:' *Technical Education IDENTIFIERS Military COrriculum Project: *Oscillators ABSTRACT This individualized learning module on intermediate oscillators is one in a series of modules for a course in basic electricity and electronics. The course is one of a number of military-developed curriculum packages selected for adaptation to vocational instructional and curriculum develbpsent in a civilian setting. Five lessons are included in the module: (1) Hartley . Oscillators,(2) Resistiye Capacitive Phase Shift Oscillators, (21 Wien.-Bridge Cscillators, (U) Blocking Oscillators, and(5) Crystal ControlledOscillators. Each lesson follows a typical format including a lesson overview, a list of study resources, the lesson content, a programmed instruction sections, and .a lesson summary. (Progress checks and other supplementary material are provided for each lesson in a students guide, CE 026 590.1 (LEA) i' *********************************************************************** * Reproductions supplied by EDRS are the best that can be jade * * from the original document. * *********************************************************************** rd. .1770.1114.131Pr Ara:AIL* %IR 6 10 411. t v-- . C:k LAJ CHIEF OF NAVAL EDUCATION AND TRAINING.1, ilitaryurrla CNTT-E-054. \\.. 4- al JULY 1980 we' Technical Education I BASIC ELECTRICITY AND ELECTRONICS'. -

Wien Bridge Oscillator Using Op-Amp for a Given Frequency of 1Khz
Experiment No. 9 WIEN BRIDGE OSCILLATOR USING OPAMP AIM: To design a Wien Bridge oscillator using op-amp for a given frequency of 1kHz. THEORY: An oscillator is a circuit that produces periodic electric signals such as sine wave or square wave. The application of oscillator includes sine wave generator, local oscillator for synchronous receivers etc. An oscillator consists of an amplifier and a feedback network. 1. 'Active device' i.e. opamp is used as an amplifier. 2. Passive components such as R-C or L-C combinations are used as feedback network. To start the oscillation with the constant amplitude, positive feedback is not the only sufficient condition. Oscillator circuit must satisfy the following two conditions known as Barkhausen conditions: 1. Magnitude of the loop gain (Av β) = 1, where, Av = Amplifier gain and β = Feedback gain. Fig 1. Basic oscillator block diagram 2. Phase shift around the loop must be 360° or 0°. Wien bridge oscillator is an audio frequency sine wave oscillator of high stability and simplicity. The feedback signal in this circuit is connected to the non-inverting input terminal so that the op-amp is working as a non-inverting amplifier. Therefore, the feedback network need not provide any phase shift. The circuit can be viewed as a Wien bridge with a series combination of R1 and C1 in one arm and parallel combination of R2 and C2 in the adjoining arm. Resistors R3 and R4 are connected in the remaining two arms. The condition of zero phase shift around the circuit is achieved by balancing the bridge.