DOCSLIB.ORG

Topic 6 Polygons and Quadrilaterals

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Topic 6 Polygons and Quadrilaterals Topic 6 Polygons and Quadrilaterals TOPIC OVERVIEW VOCABULARY 6-1 The Polygon Angle-Sum Theorems English/Spanish Vocabulary Audio Online: 6-2 Properties of Parallelograms English Spanish 6-3 Proving That a Quadrilateral equiangular polygon, p. 249 polígono equiángulo Is a Parallelogram equilateral polygon, p. 249 polígono equilátero 6-4 Properties of Rhombuses, isosceles trapezoid, p. 281 trapecio isósceles Rectangles, and Squares kite, p. 282 cometa 6-5 Conditions for Rhombuses, midsegment of a trapezoid, p. 281 segmento medio de un trapecio Rectangles, and Squares parallelogram, p. 255 paralelogramo rectangle, p. 269 rectángulo 6-6 Trapezoids and Kites regular polygon, p. 249 polígono regular rhombus, p. 269 rombo square, p. 269 cuadrado trapezoid, p. 281 trapecio DIGITAL APPS PRINT and eBook Access Your Homework . ONLINE HOMEWORK You can do all of your homework online with built-in examples and “Show Me How” support! When you log in to your account, you’ll see the homework your teacher has assigned you. HOMEWORK TUTOR APP YOUR DIGITAL Do your homework anywhere! You can access the Practice and RESOURCES Application Exercises, as well as Virtual Nerd tutorials, with this PearsonTEXAS.com Homework Tutor app, available on any mobile device. STUDENT TEXT AND HOMEWORK HELPER Access the Practice and Application Exercises that you are assigned for homework in the Student Text and Homework Helper, which is also available as an electronic book. 246 Topic 6 Polygons and Quadrilaterals The Mystery Sides Have you every looked closely at honeycombs? What shape are they? How do you know? Math Most often the cells in the honeycombs look like hexagons, but they might also look like Act Math Act Act - - circles. Scientists now believe 3 3 that the bees make circular cells that become hexagonal due to the bees’ body heat and natural physical forces. What are some strategies you use to identify shapes? Think about this as you watch the 3-Act Math video. Scan page to see a video for this 3-Act Math Task. If You Need Help . VOCABULARY ONLINE LEARNING ANIMATIONS INTERACTIVE MATH TOOLS You’ll find definitions of math You can also access all of the These interactive math tools terms in both English and stepped-out learning animations give you opportunities to Spanish. All of the terms have that you studied in class. explore in greater depth audio support. key concepts to help build understanding. INTERACTIVE EXPLORATION STUDENT COMPANION VIRTUAL NERD You’ll have access to a robust Refer to your notes and Not sure how to do some of assortment of interactive solutions in your Student the practice exercises? Check explorations, including Companion. Remember that out the Virtual Nerd videos interactive concept explorations, your Student Companion is also for stepped-out, multi-level dynamic activitites, and topic- available as an ACTIVebook instructional support. level exploration activities. accessible on any digital device. PearsonTEXAS.com 247 Technology Lab Exterior Angles of Polygons USE WITH LESSON 6-1 TEKS (5)(A), (1)(E) Use geometry software. Construct a polygon similar to the one at the right. Extend each side as shown. Mark a point on each ray so that you can measure the exterior angles. Use your figure to explore properties of a polygon. • Measure each exterior angle. • Calculate the sum of the measures of the exterior angles. • Manipulate the polygon. Observe the sum of the measures of the exterior angles of the new polygon. hsm11gmse_0601a_t06178 Exercises 1. Write a conjecture about the sum of the measures of the exterior angles (one at each vertex) of a convex polygon. Test your conjecture with another polygon. 2. The figures below show a polygon that is decreasing in size until it finally becomes a point. Describe how you could use this to justify your conjecture in Exercise 1. 1 5 5 1 4 4 5 2 1 4 3 2 3 2 3 3. The figure at the right shows a square that has been copied several times. Notice that you can use the square to completely cover, or tile, a plane, without Ӈ gapshsm11gmse_0601a_t06179 or overlaps. hsm11gmse_0601a_t06180hsm11gmse_0601a_t06181 a. Using geometry software, make several copies of other regular polygons with 3, 5, 6, and 8 sides. Regular polygons have sides of equal length and angles of equal measure. Ӈ b. Which of the polygons you made can tile a plane? c. Measure one exterior angle of each polygon (including the square). d. Write a conjecture about the relationship between the measure of an exterior angle and your ability to tile a plane with the polygon. Test your conjecture with another regular polygon. hsm11gmse_0601a_t06182 248 Technology Lab Exterior Angles of Polygons 6-1 The Polygon Angle-Sum Theorems TEKS FOCUS VOCABULARY TEKS (5)(A) Investigate patterns to make conjectures about • Equiangular polygon – An equiangular geometric relationships, including angles formed by parallel lines polygon is a polygon with all angles cut by a transversal, criteria required for triangle congruence, special congruent. segments of triangles, diagonals of quadrilaterals, interior and • Equilateral polygon – An equilateral polygon exterior angles of polygons, and special segments and angles of circles is a polygon with all sides congruent. choosing from a variety of tools. • Regular polygon – A regular polygon is TEKS (1)(C) Select tools, including real objects, manipulatives, paper and a polygon that is both equilateral and pencil, and technology as appropriate, and techniques, including mental equiangular. math, estimation, and number sense as appropriate, to solve problems. Additional TEKS (1)(E), (1)(F) • Number sense – the understanding of what numbers mean and how they are related ESSENTIAL UNDERSTANDING The sum of the interior angle measures of a polygon depends on the number of sides the polygon has. Key Concept Classifying Polygons Based on Sides and Angles An equilateral polygon An equiangular polygon A regular polygon is is a polygon with all is a polygon with all a polygon that is both sides congruent. angles congruent. equilateral and equiangular. Theorem 6-1 Polygonhsm11gmse_0601_t06300 Angle-Sum Theorem hsm11gmse_0601_t06299 hsm11gmse_0601_t06301 The sum of the measures of the interior angles of an n-gon is (n - 2)180. For a proof of Theorem 6-1, see the Reference section on page 683. Corollary to the Polygon Angle-Sum Theorem (n - 2)180 The measure of each interior angle of a regular n-gon is n . You will prove the Corollary to the Polygon Angle-Sum Theorem in Exercise 16. PearsonTEXAS.com 249 Theorem 6-2 Polygon Exterior Angle-Sum Theorem The sum of the measures of the exterior angles of a polygon, one at 3 2 each vertex, is 360. For the pentagon, m∠1 + m∠2 + m∠3 + m∠4 + m∠5 = 360. 4 1 5 You will prove Theorem 6-2 in Exercise 9. Problem 1 TEKShsm11gmse_0601_t06313.ai Process Standard (1)(C) Investigating Interior Angles of Polygons A Choose from among a variety of tools (such as a ruler, a compass, or geometry software) to investigate the sums of the measures of the interior angles of different polygons. Explain your choice. Geometry software is a good way to identify the measures of the interior angles of polygons. You can quickly make many different polygons and use the software to find the measures of their angles. B Use geometry software to make several triangles, quadrilaterals, pentagons, and hexagons. Then complete the table. Sum of Interior Angle Sum of Interior Angle Polygon Measures Polygon Measures Triangle 1 180 Pentagon 1 540 Triangle 2 180 Pentagon 2 540 Triangle 3 180 Pentagon 3 540 Quadrilateral 1 360 Hexagon 1 720 Quadrilateral 2 360 Hexagon 2 720 Quadrilateral 3 360 Hexagon 3 720 How can recording data in a table C Use the data in the table in part B to make a conjecture about the sum of the help you make a measures of the interior angles of a polygon. conjecture? Recording data in a table Notice that the numbers in the table are all multiples of 180. Look at the patterns: is an organized way to present and analyze Triangle 1 # 180 = 180 Pentagon 3 # 180 = 540 information. You can look Quadrilateral 2 180 360 Hexagon 4 180 720 for patterns in the data # = # = and make a conjecture. Conjecture: If you subtract 2 from the number of sides and multiply by 180, you will get the sum of the measures of the interior angles of any polygon. 250 Lesson 6-1 The Polygon Angle-Sum Theorems Problem 2 Finding a Polygon Angle Sum How many sides does What is the sum of the interior angle measures of a heptagon? a heptagon have? A heptagon has 7 sides. Sum = (n - 2)180 Polygon Angle-Sum Theorem = (7 - 2)180 Substitute 7 for n. = 5 # 180 Simplify. = 900 The sum of the interior angle measures of a heptagon is 900. Problem 3 Using the Polygon Angle-Sum Theorem STEM Biology The common housefly, Musca domestica, has eyes How does the word that consist of approximately 4000 facets. Each facet is regular help you a regular hexagon. What is the measure of each answer the question? interior angle in one hexagonal facet? The word regular tells you that each angle has the same measure. (n - 2)180 Measure of an angle = n Corollary to the Polygon Angle-Sum Theorem (6 - 2)180 = 6 Substitute 6 for n. 4 # 180 = 6 Simplify. = 120 The measure of each interior angle in one hexagonal facet is 120. PearsonTEXAS.com 251 Problem 4 Using the Polygon Angle-Sum Theorem What is mjY in pentagon TODAY? How does the T diagram help you? Use the Polygon Angle-Sum Theorem for n = 5. 110Њ You know the number of O sides and four of the five m∠T + m∠O + m∠D + m∠A + m∠Y = (5 - 2)180 Y angle measures.
Load more

Recommended publications
  • 1 Point for the Player Who Has the Shape with the Longest Side. Put
    Put three pieces together to create a new 1 point for the player who has the shape. 1 point for the player who has shape with the longest side. the shape with the smallest number of sides. 1 point for the player who has the 1 point for the player with the shape that shape with the shortest side. has the longest perimeter. 1 point for the player with the shape that 1 point for each triangle. has the largest area. 1 point for each shape with 1 point for each quadrilateral. a perimeter of 24 cm. Put two pieces together to create a new shape. 1 point for the player with 1 point for each shape with the shape that has the longest a perimeter of 12 cm. perimeter. Put two pieces together to create a new shape. 1 point for the player with 1 point for each shape with the shape that has the shortest a perimeter of 20 cm. perimeter. 1 point for each 1 point for each shape with non-symmetrical shape. a perimeter of 19 cm. 1 point for the shape that has 1 point for each the largest number of sides. symmetrical shape. Count the sides on all 5 pieces. 1 point for each pair of shapes where the 1 point for the player who has the area of one is twice the area of the other. largest total number of sides. Put two pieces together to create a new shape. 1 point for the player who has 1 point for each shape with at least two the shape with the fewest number of opposite, parallel sides.
    [Show full text]
  • Extremal Problems for Convex Polygons ∗
    Extremal Problems for Convex Polygons ∗ Charles Audet Ecole´ Polytechnique de Montreal´ Pierre Hansen HEC Montreal´ Fred´ eric´ Messine ENSEEIHT-IRIT Abstract. Consider a convex polygon Vn with n sides, perimeter Pn, diameter Dn, area An, sum of distances between vertices Sn and width Wn. Minimizing or maximizing any of these quantities while fixing another defines ten pairs of extremal polygon problems (one of which usually has a trivial solution or no solution at all). We survey research on these problems, which uses geometrical reasoning increasingly complemented by global optimization meth- ods. Numerous open problems are mentioned, as well as series of test problems for global optimization and nonlinear programming codes. Keywords: polygon, perimeter, diameter, area, sum of distances, width, isoperimeter problem, isodiametric problem. 1. Introduction Plane geometry is replete with extremal problems, many of which are de- scribed in the book of Croft, Falconer and Guy [12] on Unsolved problems in geometry. Traditionally, such problems have been solved, some since the Greeks, by geometrical reasoning. In the last four decades, this approach has been increasingly complemented by global optimization methods. This allowed solution of larger instances than could be solved by any one of these two approaches alone. Probably the best known type of such problems are circle packing ones: given a geometrical form such as a unit square, a unit-side triangle or a unit- diameter circle, find the maximum radius and configuration of n circles which can be packed in its interior (see [46] for a recent survey and the site [44] for a census of exact and approximate results with up to 300 circles).
    [Show full text]
  • Chapter 6: Things to Know
    MAT 222 Chapter 6: Things To Know Section 6.1 Polygons Objectives Vocabulary 1. Define and Name Polygons. • polygon 2. Find the Sum of the Measures of the Interior • vertex Angles of a Quadrilateral. • n-gon • concave polygon • convex polygon • quadrilateral • regular polygon • diagonal • equilateral polygon • equiangular polygon Polygon Definition A figure is a polygon if it meets the following three conditions: 1. 2. 3. The endpoints of the sides of a polygon are called the ________________________ (Singular form: _______________ ). Polygons must be named by listing all of the vertices in order. Write two different ways of naming the polygon to the right below: _______________________ , _______________________ Example Identifying Polygons Identify the polygons. If not a polygon, state why. a. b. c. d. e. MAT 222 Chapter 6 Things To Know Number of Sides Name of Polygon 3 4 5 6 7 8 9 10 12 n Definitions In general, a polygon with n sides is called an __________________________. A polygon is __________________________ if no line containing a side contains a point within the interior of the polygon. Otherwise, a polygon is _________________________________. Example Identifying Convex and Concave Polygons. Identify the polygons. If not a polygon, state why. a. b. c. Definition An ________________________________________ is a polygon with all sides congruent. An ________________________________________ is a polygon with all angles congruent. A _________________________________________ is a polygon that is both equilateral and equiangular. MAT 222 Chapter 6 Things To Know Example Identifying Regular Polygons Determine if each polygon is regular or not. Explain your reasoning. a. b. c. Definition A segment joining to nonconsecutive vertices of a convex polygon is called a _______________________________ of the polygon.
    [Show full text]
  • Discovering Geometry an Investigative Approach
    Discovering Geometry An Investigative Approach Condensed Lessons: A Tool for Parents and Tutors Teacher’s Materials Project Editor: Elizabeth DeCarli Project Administrator: Brady Golden Writers: David Rasmussen, Stacey Miceli Accuracy Checker: Dudley Brooks Production Editor: Holly Rudelitsch Copyeditor: Jill Pellarin Editorial Production Manager: Christine Osborne Production Supervisor: Ann Rothenbuhler Production Coordinator: Jennifer Young Text Designers: Jenny Somerville, Garry Harman Composition, Technical Art, Prepress: ICC Macmillan Inc. Cover Designers: Jill Kongabel, Marilyn Perry, Jensen Barnes Printer: Data Reproductions Textbook Product Manager: James Ryan Executive Editor: Casey FitzSimons Publisher: Steven Rasmussen ©2008 by Kendall Hunt Publishing. All rights reserved. Cover Photo Credits: Background image: Doug Wilson/Westlight/Corbis. Construction site image: Sonda Dawes/The Image Works. All other images: Ken Karp Photography. Limited Reproduction Permission The publisher grants the teacher whose school has adopted Discovering Geometry, and who has received Discovering Geometry: An Investigative Approach, Condensed Lessons: A Tool for Parents and Tutors as part of the Teaching Resources package for the book, the right to reproduce material for use in his or her own classroom. Unauthorized copying of Discovering Geometry: An Investigative Approach, Condensed Lessons: A Tool for Parents and Tutors constitutes copyright infringement and is a violation of federal law. All registered trademarks and trademarks in this book are the property of their respective holders. Kendall Hunt Publishing 4050 Westmark Drive PO Box 1840 Dubuque, IA 52004-1840 www.kendallhunt.com Printed in the United States of America 10 9 8 7 6 5 4 3 2 13 12 11 10 09 08 ISBN 978-1-55953-895-4 Contents Introduction .
    [Show full text]
  • Polygons and Convexity
    Geometry Week 4 Sec 2.5 to ch. 2 test section 2.5 Polygons and Convexity Definitions: convex set – has the property that any two of its points determine a segment contained in the set concave set – a set that is not convex concave concave convex convex concave Definitions: polygon – a simple closed curve that consists only of segments side of a polygon – one of the segments that defines the polygon vertex – the endpoint of the side of a polygon 1 angle of a polygon – an angle with two properties: 1) its vertex is a vertex of the polygon 2) each side of the angle contains a side of the polygon polygon not a not a polygon (called a polygonal curve) polygon Definitions: polygonal region – a polygon together with its interior equilateral polygon – all sides have the same length equiangular polygon – all angels have the same measure regular polygon – both equilateral and equiangular Example: A square is equilateral, equiangular, and regular. 2 diagonal – a segment that connects 2 vertices but is not a side of the polygon C B C B D A D A E AC is a diagonal AC is a diagonal AB is not a diagonal AD is a diagonal AB is not a diagonal Notation: It does not matter which vertex you start with, but the vertices must be listed in order. Above, we have square ABCD and pentagon ABCDE. interior of a convex polygon – the intersection of the interiors of is angles exterior of a convex polygon – union of the exteriors of its angles 3 Polygon Classification Number of sides Name of polygon 3 triangle 4 quadrilateral 5 pentagon 6 hexagon 7 heptagon 8 octagon
    [Show full text]
  • Englewood Public School District Geometry Second Marking Period
    Englewood Public School District Geometry Second Marking Period Unit 2: Polygons, Triangles, and Quadrilaterals Overview: During this unit, students will learn how to prove two triangles are congruent, relationships between angle measures and side lengths within a triangle, and about different types of quadrilaterals. Time Frame: 35 to 45 days (One Marking Period) Enduring Understandings: • Congruent triangles can be visualized by placing one on top of the other. • Corresponding sides and angles can be marked using tic marks and angle marks. • Theorems can be used to prove triangles congruent. • The definitions of isosceles and equilateral triangles can be used to classify a triangle. • The Midpoint Formula can be used to find the midsegment of a triangle. • The Distance Formula can be used to examine relationships in triangles. • Side lengths of triangles have a relationship. • The negation statement can be proved and used to show a counterexample. • The diagonals of a polygon can be used to derive the formula for the angle measures of the polygon. • The properties of parallel and perpendicular lines can be used to classify quadrilaterals. • Coordinate geometry can be used to classify special parallelograms. • Slope and the distance formula can be used to prove relationships in the coordinate plane. Essential Questions: • How do you identify corresponding parts of congruent triangles? • How do you show that two triangles are congruent? • How can you tell if a triangle is isosceles or equilateral? • How do you use coordinate geometry
    [Show full text]
  • Midsegment of a Trapezoid Parallelogram
    Vocabulary Flash Cards base angles of a trapezoid bases of a trapezoid Chapter 7 (p. 402) Chapter 7 (p. 402) diagonal equiangular polygon Chapter 7 (p. 364) Chapter 7 (p. 365) equilateral polygon isosceles trapezoid Chapter 7 (p. 365) Chapter 7 (p. 402) kite legs of a trapezoid Chapter 7 (p. 405) Chapter 7 (p. 402) Copyright © Big Ideas Learning, LLC Big Ideas Math Geometry All rights reserved. Vocabulary Flash Cards The parallel sides of a trapezoid Either pair of consecutive angles whose common side is a base of a trapezoid A polygon in which all angles are congruent A segment that joins two nonconsecutive vertices of a polygon A trapezoid with congruent legs A polygon in which all sides are congruent The nonparallel sides of a trapezoid A quadrilateral that has two pairs of consecutive congruent sides, but opposite sides are not congruent Copyright © Big Ideas Learning, LLC Big Ideas Math Geometry All rights reserved. Vocabulary Flash Cards midsegment of a trapezoid parallelogram Chapter 7 (p. 404) Chapter 7 (p. 372) rectangle regular polygon Chapter 7 (p. 392) Chapter 7 (p. 365) rhombus square Chapter 7 (p. 392) Chapter 7 (p. 392) trapezoid Chapter 7 (p. 402) Copyright © Big Ideas Learning, LLC Big Ideas Math Geometry All rights reserved. Vocabulary Flash Cards A quadrilateral with both pairs of opposite sides The segment that connects the midpoints of the parallel legs of a trapezoid PQRS A convex polygon that is both equilateral and A parallelogram with four right angles equiangular A parallelogram with four congruent sides and four A parallelogram with four congruent sides right angles A quadrilateral with exactly one pair of parallel sides Copyright © Big Ideas Learning, LLC Big Ideas Math Geometry All rights reserved.
    [Show full text]
  • Chapter 1: Tools of Geometry
    Tools of Geometry Then You graphed points on the coordinate plane and evaluated mathematical expressions. Now In Chapter 1, you will: Find distances between points and midpoints of line segments. Identify angle relationships. Find perimeters, areas, surface areas, and volumes. KY Program of Studies HS-G-S-SR6 Students will analyze and apply spatial relationships among points, lines and planes. HS-G-S-FS4 Students will perform constructions. Why? MAPS Geometric figures and terms can be used to represent and describe real-world situations. On a map, locations of cities can be represented by points, highways or streets by lines, and national parks by polygons that have both perimeter and area. The map itself is representative of a plane. Animation glencoe.com 2 Chapter 1 Tools of Geometry Get Ready for Chapter 1 Diagnose Readiness You have two options for checking Prerequisite Skills. Text Option Take the Quick Check below. Refer to the Quick Review for help. QuickCheck QuickReview Graph and label each point in the coordinate EXAMPLE 1 (Lesson 0-7) plane. Graph and label the point Q(−3, 4) in the 1. W(5, 2) 2. X(0, 6) coordinate plane. 3. Y(-3, -1) 4. Z(4, 2) Start at the origin. y Since the x-coordinate 2 -3, 4 abcdef g h 5. GAMES Carolina is is negative, move 3 using the diagram to 8 8 7 7 units to the left. Then record her chess 6 6 move 4 units up since moves. She moves 5 5 0 the y-coordinate is x her knight 2 spaces 4 4 3 3 positive.
    [Show full text]
  • Side of the Polygon Polygon Vertex of the Diagonal Sides Angles Regular
    King Geometry – Chapter 6 – Notes and Examples Section 1 – Properties and Attributes of Polygons Each segment that forms a polygon is a _______side__ _ of ____ _the____ ______________. polygon The common endpoint of two sides is a ____________vertex _____of _______ the ________________polygon . A segment that connects any two nonconsecutive vertices is a _________________.diagonal Number of Sides Name of Polygon You can name a polygon by the number of its 3 Triangle sides. The table shows the names of some common polygons. 4 Quadrilateral 5 Pentagon If the number of sides is not listed in the table, then the polygon is called a n-gon where n 6 Hexagon represents the number of sides. Example: 16 sided figure is called a 16-gon 7 Heptagon 8 Octagon Remember! A polygon is a closed plane figure formed by 9 Nonagon three or more segments that intersect only at their endpoints. 10 Decagon 12 Dodecagon n n-gon All of the __________sides are congruent in an equilateral polygon. All of the ____________angles are congruent in an equiangular polygon. A __________________________regular polygon is one that is both equilateral and equiangular. If a polygon is ______not regular, it is called _________________irregular . A polygon is ______________concave if any part of a diagonal contains points in the exterior of the polygon. If no diagonal contains points in the exterior, then the polygon is ____________convex . A regular polygon is always _____________convex . Examples: Tell whether the figure is a polygon. If it is a polygon, name it by the number of sides. not a not a polygon, not a polygon, heptagon polygon hexagon polygon polygon Tell whether the polygon is regular or irregular.
    [Show full text]
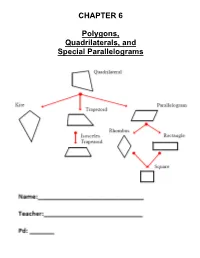
  • CHAPTER 6 Polygons, Quadrilaterals, and Special Parallelograms
    CHAPTER 6 Polygons, Quadrilaterals, and Special Parallelograms Table of Contents DAY 1: (Ch. 6-1) SWBAT: Find measures of interior and exterior angles of polygons Pgs: 1-7 HW: Pgs: 8-10 DAY 2: (6-2) SWBAT: Solve Problems involving Parallelograms Pgs: 11-16 HW: Pgs: 17-18 DAY 3: (6-4) SWBAT: Solve Problems involving Rectangles Pgs: 19-22 HW: Pg: 23 DAY 4: (6-4) SWBAT: Solve Problems involving Rhombi and Squares Pgs: 24-28 HW: Pgs: 29-30 DAY 5: (6-6) SWBAT: Solve Problems involving Trapezoids Pgs: 31-36 HW: Pgs: 37-39 DAY 6-7: (Review) SWBAT: Review of Quadrilaterals Pgs: 40-52 HW: Finish this section for homework Chapter 6 (Section 1) – Day 1 Angles in polygons A polygon is a closed plane figure formed by three or more segments that intersect only at their endpoints. Each segment that forms a polygon is a side of the polygon. The common endpoint of two sides is a vertex of the polygon. A segment that connects any two nonconsecutive vertices is a diagonal. You can name a polygon by the number of its sides. The table shows the names of some common polygons. All the sides are congruent in an equilateral polygon. All the angles are congruent in an equiangular polygon. A regular polygon is one that is both equilateral and equiangular. If a polygon is not regular, it is called irregular. A polygon is concave if any part of a diagonal contains points in the exterior of the polygon. If no diagonal contains points in the exterior, then the polygon is convex.
    [Show full text]
  • Sensitivity Studies for the Exercise I-1 of the OECD/UAM Benchmark
    Hindawi Publishing Corporation Science and Technology of Nuclear Installations Volume 2012, Article ID 817185, 10 pages doi:10.1155/2012/817185 Research Article Sensitivity Studies for the Exercise I-1 of the OECD/UAM Benchmark E. Canuti,1 A. Petruzzi,1 F. D’Auria, 1 and T. Kozlowski2 1 San Piero a Grado Nuclear Research Group (GRNSPG), University of Pisa, Via Diotisalvi 2, 56122 Pisa, Italy 2 Department of Nuclear, Plasma, and Radiological Engineering, University of Illinois, 216 Talbot Laboratory, MC-234, 104 South Wright Street, Urbana, IL 61801, USA Correspondence should be addressed to E. Canuti, [email protected] Received 24 August 2012; Revised 30 October 2012; Accepted 31 October 2012 Academic Editor: Oscar Cabellos Copyright © 2012 E. Canuti et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. OECD/NEA has initiated an international Uncertainty Analysis in Modeling (UAM) benchmark focused on uncertainties in modeling of Light Water Reactor (LWR). The first step of uncertainty propagation is to perform sensitivity to the input data affected by the numerical errors and physical models. The objective of the present paper is to study the effect of the numerical discretization error and the manufacturing tolerances on fuel pin lattice integral parameters (multiplication factor and macroscopic cross- sections) through sensitivity calculations. The two-dimensional deterministic codes NEWT and HELIOS were selected for this work. The NEWT code was used for analysis of the TMI-1, PB-2, and Kozloduy-6 test cases; the TMI-1 test case was investigated using the HELIOS code.
    [Show full text]
  • CH3 Test: Polygons, Quadrilaterals and Circles
    MTH 351 Review Sheet 1 CH3 Test: Polygons, Quadrilaterals and Circles Polygons Definition – How do we define polygons? Vocabulary : Side, Vertex, Diagonal, Interior angle, Exterior angle; Regular polygon Convexity and concavity of figures and polygons – what is a convex/non-convex figure? Make sure you know to classify figures such as those on the right. Classification of polygons. How do we classify/name polygons? What is a regular polygon? Interior angles sum . Find the sum of interior angles of (any) given polygon (see pictures). You also should be able to derive (justify) the formula for interior angle sum of a n-sided polygon. (Hint: recall #2 and 3 on pg.56) Find an interior angle of a regular pentagon. (Hint: First find the sum of all interior angles in a pentagon and then calculate the measure of one angle.) True or false? If it is false, draw a counterexample. • A regular polygon is always equilateral. • An equiangular polygon is also equilateral. • Pentagon that has all sides congruent is a regular pentagon. Etc. Quadrilaterals Definition – How do we define quadrilaterals? What do you know about the definitions of a trapezoid and kite? Each has two significantly different definitions - explain the difference (“modern” and “traditional”). Classification of quadrilaterals. Use Venn Diagram to classify quadrilaterals (use the traditional definitions of trapezoid and kite). Draw a typical representative in each region of your Venn Diagram. How would the diagram change if you were to use trapezoid’s “modern” definition? Answer the following questions or decide if the statements are true or false and justify your answer.
    [Show full text]